鐵磁納米線中磁化強度的磁怪波*
李再東 郭奇奇
1) (河北工業大學理學院, 天津 300401)
2) (天津理工大學理學院, 天津 300384)
本文介紹了鐵磁納米線中磁化強度的一些新激發態, 包括各向同性鐵磁的Akhmediev呼吸子、Kuznetsov-Ma孤子和怪波、自旋極化電流驅動下各向異性鐵磁納米線中的怪波動力學.在各向同性情況下,展示了形如四片花瓣的磁孤子的空間周期過程和自旋波背景的局域化過程; 在極限情況下, 得到了磁怪波解并闡明了其形成機制.在各向異性情況下, 發現怪波的產生主要源于中心的能量積累和快速彌散; 此外, 怪波還具有不穩定性, 它和自旋波背景間的能量與磁振子的交換可以通過自旋極化電流來調控.
專題:非線性物理
1 引 言
在過去幾十年中, 磁性納米結構的磁化動力學研究取得了重大進展.在這些研究中, Selforganization[1]是自然界中最有趣的物理現象之一.在磁學領域中, 這一現象已經在條狀疇、磁泡、磁孤子、磁渦旋等磁疇的形成方面進行了深入細致的研究.此外, 在二維薄膜磁性系統的研究中, 一些有趣的磁性Self-organization模式進一步被揭示,如自旋波[2]和斯格明子[3?5], 其中斯格明子可以在薄膜中作為亞穩態成核.基于斯格明子在納米軌道上的運動為設計磁性信息存儲器提供了新的路徑.
疇壁的動力學引起諸多研究興趣, 主要原因在于其潛在的技術應用價值在未來信息存儲和讀取方面具有廣闊前景和重要意義[6?11].例如, 在鐵磁體中, 磁化強度形成的空間局域結構-磁疇壁, 其實可以看作是一個勢壘, 將簡并的兩個磁狀態分開[12,13],而這兩個組態正好可以作為二進制信息存儲的基本單元.目前, 疇壁運動有多種驅動手段, 例如外磁場、自旋轉移矩和磁振子等, 但疇壁的傳播還受到自旋霍爾效應[14]、Rashba效應[15]和Dzyaloshinskii-Moriya 相互作用[16?19]的影響.近些年來, Dzyaloshinskii-Moriya相互作用引起了人們對低維磁學的極大興趣[16?23], 這些研究不僅受到基本物理問題的啟發, 還受到自旋電子存儲器和邏輯納米器件潛在應用的啟發.Dzyaloshinskii-Moriya相互作用可以看作是一種各向異性超交換作用, 不僅對疇壁運動具有重要影響, 而且對孤子的激發和傳播也存在重要影響.研究表明Dzyaloshinskii-Moriya相互作用可以影響孤子能量, 從而改變了動態孤子的振幅及內部結構畸變,形成不同結構類型的孤子[17].另外, Dzyaloshinskii-Moriya相互作用還存在于反鐵磁和弱鐵磁中, 同樣對其孤子激發有著重要影響[24?26].
此外, 層狀材料中與自旋極化電流有關的磁化動力學問題也得到了廣泛的關注[27,28].自旋極化電流可以在磁性多層結構中引起許多獨特的現象[29,30],如自旋波激發[31,32]、磁化開關[27]和反轉[33?35]及吉爾伯特阻尼增強[36,37]等.目前, 自旋極化電流通常用來創建、操縱和控制納米尺度的磁激發, 例如疇壁[38?41]和渦旋[42?44].眾所周知, 非線性激發[12,13]是磁性有序材料中的一般現象.在鐵磁體中, 磁振子由于相互吸引作用而趨于自局域化.在某種意義上, 磁振子的吸引力對于一維鐵磁體是至關重要的, 因為它產生準粒子(磁振子)的束縛態, 即自局域化.自旋波可以被看作是宏觀上連續的磁振子簇, 當磁化強度偏離基態時就會引起自旋波的激發, 它們的相互作用和不穩定性導致了磁疇壁和磁孤子的存在.
然而, 非線性激發的研究還有待于進一步深化.近年來, 小局部擾動是非線性物理研究的熱點之一.研究表明, 呼吸子或怪波可以由高階效應、非自治和耦合效應在一定條件下轉化為各種非線性波[45?49], 從而導致呼吸子和孤子之間實現狀態轉換.基于線性穩定性分析調制不穩定性, 從而分析該狀態躍遷的機制已經得到大量研究[45?47], 但是當擾動增長與背景相當大時, 線性分析不再有效.因此, 在 2013年, Zakharov 和 Gelash[50,51]提出了一種由小的局部擾動發展而來的超正則呼吸子解, 可以用來描述調制不穩定的非線性階段.并且近年來, 在一些具有高階效應的光纖系統, 例如Hirota and Maxwell-Bloch 等系統中, 這種超正則呼吸子動力學和它們的狀態轉換也得到了詳細研究[48,49].眾所周知, 調制不穩定性存在于光纖、玻色-愛因斯坦凝聚等眾多非線性系統中, 這些結果不僅豐富了調制不穩定性的內涵, 也為其他各種系統的非線性研究提供了方法.
本文研究在磁學系統中, 當自旋波通過磁孤子時, 自旋角動量從傳播的磁振子傳遞給孤子的現象, 這被稱為全磁的自旋轉移力矩[52].這種全磁的自旋轉移力矩可以影響磁化動力學, 使磁狀態發生改變.本文研究了自旋波背景下鐵磁納米線中磁化強度的呼吸子和怪波解, 討論了各向同性情況下由全磁的自旋轉移力矩引起的亮(暗)怪波的精確解,以及自旋極化電流驅動下的單軸各向異性的怪波動力學, 這些研究結果預期對玻色子和費米子鐵磁體的非線性激發的探測具有一定的意義.
2 Landau-Lifshitz-Gilbert方程
鐵磁中磁化強度的動力學可以用著名的Landau-Lifshitz-Gilbert方程很好地描述.本文采用無量綱形式[53]
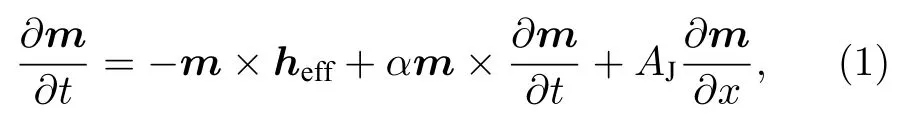
其中,α為吉爾伯特阻尼系數;AJ表示絕熱自旋矩參數;heff表示有效場, 包括交換場、各向異性場和外加磁場.對于垂直各向異性的鐵磁納米線樣品材料, 即其中Ms為飽和磁化強度,Hk為各向異性常數,hext為所施加的外磁場.
3 各向同性的精確呼吸子解和怪波解
首先, 本文考慮簡單的各向同性模型, 即方程(1)可重新寫為
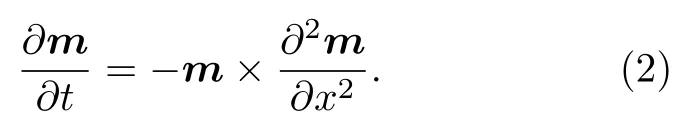
眾所周知, 該方程存在自旋波解和孤子解.需要指出的是, 方程(1)是完全可積的, 可以利用達布變換構造方程(2)的精確呼吸子解和怪波解, 這種方法的關鍵思想是首先從方程的一個種子解出發, 然后通過Lax方程的規范變換構造無窮多的新解析解.本文以自旋波作為初始的“種子”解m0, 即其中δ=ksx?ωst.將這個解帶入到方程(2), 得到色散關系為通過規范的達布變換, 可得到方程(2)的精確解形式為[54]
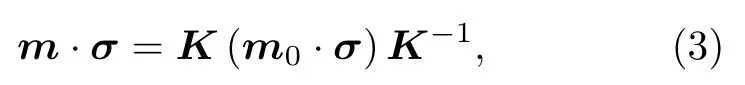
其中,σ是泡利矩陣, 矩陣K為
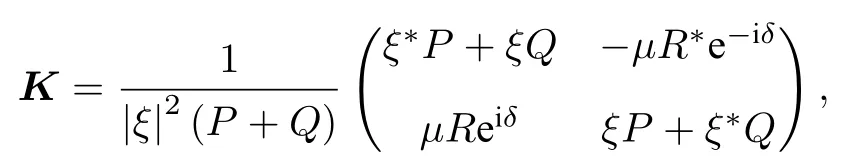
其中,
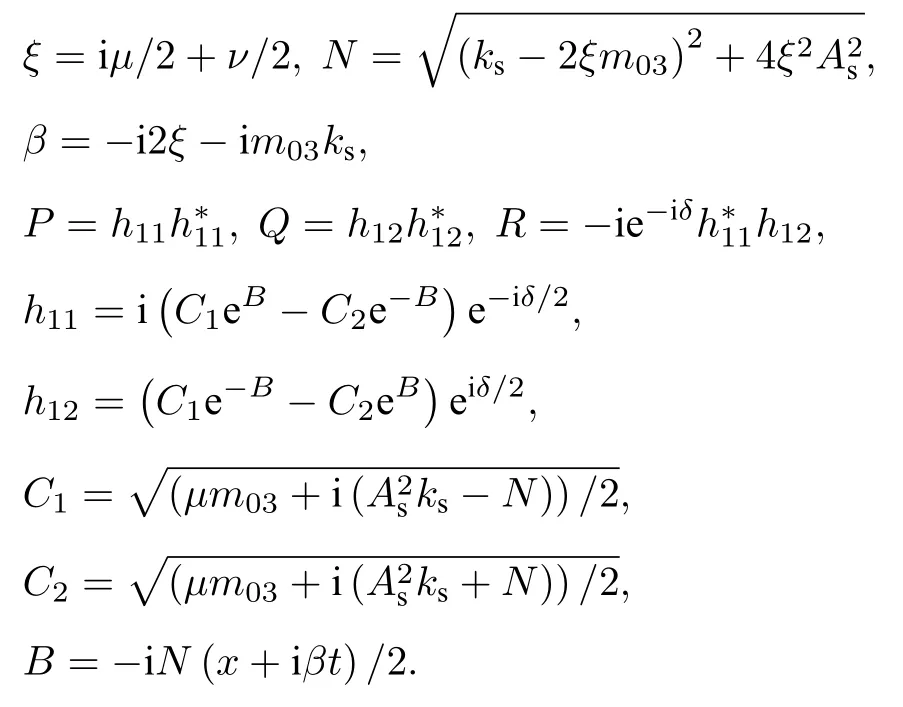
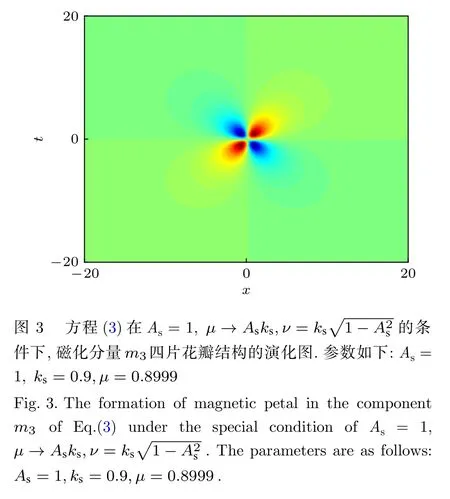
方程(3)表示嵌入到自旋波背景的磁孤子解.隨著μ的增加, 自旋波背景逐漸趨于局部化, 并且由于孤子和自旋波背景之間的相互作用形成呼吸子.仔細分析方程(3)的解, 可以得到Akhmediev呼吸子、Kuznetsov-Ma孤子及磁怪波.結果發現不同的磁狀態取決于一個臨界值 |μ|=Asks, 它也是調制不穩定過程 ( |μ|
調制不穩定性在非線性物理學中被廣泛研究[54?56], 其特征是小擾動和連續波背景之間的周期性能量交換.它可以用于在非線性光纖中產生高重復率脈沖, 可以精確地描述非線性薛定諤方程的 Akhmediev 呼吸子.在光纖中, Akhmediev 呼吸子具有時間周期性, 在傳播方向上表現出單一生長-返回循環的特性, 即著名的 Fermi-Pasta-Ulam循環[57].近年來, 調制不穩定性已被發現在各種非線性物理系統中, 對高度局域化怪波的產生起著重要作用.
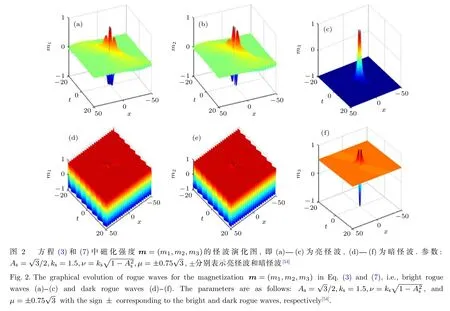
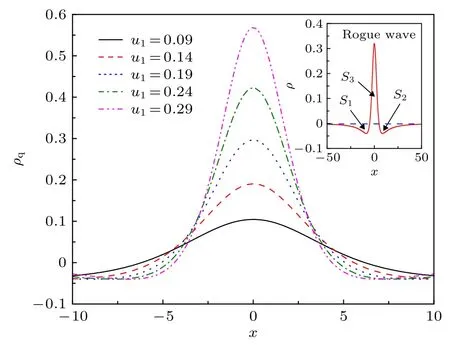
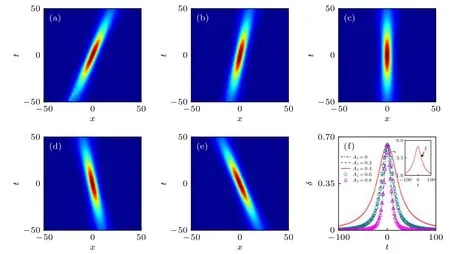
方程 (3)可以在 |μ| 這 里As=1 , 由 于x0>0,?=exp(?x0) 是 一 個小量. 通過參數方程(4)式表達的Akhmediev呼吸子解, 實際上表示自旋波背景的不穩定過程, 即在自旋波背景下的小擾動, 這些小擾動隨著時間的推移可呈現指數形式放大的非線性過程.在這個過程中, 磁孤子和自旋波背景之間發生周期性磁振子交換.應當注意的是, 在基態背景上激發的磁孤子沒有這種特性.由此說明, 正是自旋波和磁孤子之間的相互作用導致了這一非常有趣的現象. 另外, 在 |μ|>Asks和ν=ksm03的條件下, 可以得到方程(2)另外一種形式的磁激發態, 它類似于非線性光纖中光脈沖傳播的Kuznetsov-Ma孤子解, 也可以看作是怪波流體力學的原型.經過化簡后, 該解的主要特征參數如下: 由(6)式可知, 磁性Kuznetsov-Ma孤子的主要特性表現為具有時間周期性而空間具有非周期性, 且孤子的傳播速度為 ? 2ksm03, 寬度為 1 /ζ.當As=1時, 參數θ僅取決于x, 這意味著包絡速度變為零, 孤子被自旋波囚禁在空間中, 這是極為有趣的現象, 等待進一步深化研究.為了研究Kuznetsov-Ma孤子的漸近形式, 考慮極限情況x→ ±∞.根 據 方 程 (3)和 (6),m3近 似 為而 橫 向 分 量 表 示 為m+, 近 似 為這 里m0+≡m01+im02.當自旋波通過磁孤子時, 這一結果表明自旋波相位改變了自旋波的這種相位改變會影響磁孤子的傳播速度, 表示自旋角動量從自旋波背景轉移到動態孤子, 也就是前面說到的全磁自旋轉移力矩效應.另外, 要想實現m3的零背景情形, 可以通過兩種情況來實現,即As=1 或 1 /2As<1,|μ1|=ks/2 , 而在x→ ±∞時磁振子密度分布達到最大值1.因此,m3的最大和最小的演化與孤子的傳播方向相同, 這一特性說明了孤子在鐵磁體磁化周期解的背景下傳播時的呼吸特性. 方程(3)的磁性Kuznetsov-Ma孤子解不同于磁性Akhmediev呼吸子解, 方程(6)的局部周期性磁振子交換表現為時間周期性演化.因此, 高磁振子密度沿著孤子的傳播方向呈時間周期性變化.上述的討論表明, |μ|=Asks是一個臨界點條件, 劃分了調制不穩定性過程 ( |μ| 非常有趣的是, 在 |μ| 趨于 (Asks) 的極限情況下, 可以得到方程(3)的一種全新的磁化強度激發態, 它是一個有理解的形式, 稱之為磁怪波, 其中主要參數由下式給出: 這里符號 ± 表示 |μ|→ ±Asks的極限情況.為了研究方程 (7)磁怪波的漸近形式, 考慮x→ ±∞(t→ ±∞)和x→0(t→0) 的 情 況 .對于+的 情 況, 當x→ ±∞(t→ ±∞) 時m3近似 為當x→0(t→0) 時分量m3近似為m03; 而對于 ? 的情況, 當x→ ±∞(t→ ±∞) 時m3近 似 為m03, 當x→0(t→0) 時 分 量m3近 似 為對于橫向分量m+, 在+的情況, 當x→ ±∞ (t→ ±∞)時 近 似 為當x→0(t→0)時 分 量m+近 似 為 ?m0+; 在 ? 的 情況, 當x→ ±∞(t→ ±∞) 時分量m+近似為 ?m0+,當x→0(t→0) 時 近 似為上 述 分析表明情況+表示亮怪波, 而情況 ? 對應于暗怪波.亮和暗怪波的圖形表示如圖2所示. 特別的, 當As=1 時, 可以得到磁怪波如下: 上述結果表明, 磁怪波的形成存在兩種過程:一個是自旋波背景的局部化過程, 另一種是亮孤子的周期化的還原過程.磁怪波是由磁振子交換和高密度的強時間和空間局域化表現出來的.而且, 磁怪波可以通過自旋波背景的小局部擾動激發. 在這個部分, 本文考慮自旋極化電流驅動下各向異性鐵磁納米線中的磁怪波動力學, 這種情況下方程(1)是不可積的, 為了達到這個目的, 需要對方程(1)做一些近似處理和變換.方程(1)有兩種基本激發態, 即自旋波和動力學孤子, 這兩種激發態都源于磁矩對基態的微小偏移.因此, 在各向異性情況可以引入一個合理的函數q替換磁化強度的分量, 即q≡mx+imy和在考慮無阻尼和長波近似的條件下, 方程(1)可以轉變成可積的非線性薛定諤方程的形式: 其中ω0=1+hext/(Hk/Ms?4π).根據前面談到的達布變換的思想, 方程(9)的解析解很容易構造出來[58?62].這里, 選擇單軸各向異性情況下的自旋波解作為初始種子解q=Ace?i(kcx?ωct) , 其中ωc 和kc分別為無量綱的頻率和波數.經過復雜的計算, 可以得到具有呼吸特性的孤子解[53]. 與各向同性討論的類似, 在臨界點μ1=Ac且ν1= ?kc的條件下, 可得到調制不穩定過程(μ1 圖4 不同的參數 μ1 下的磁振子密度分布圖 [53], 范圍從0.09到0.29間隔0.05.插圖為怪波形成時的磁振子密度.其余參數為Ac=0.2,AJ=kc=0.1Fig.4.The magnon density distribution against the background for the different parameter μ1 , which ranges from 0.09 to 0.29 in 0.05 steps[53].The inset figure is the magnon density distribution against the background for the excited formation of magnetic rogue wave.Other parameters are Ac=0.2,AJ=kc=0.1. 根據方程(10)和ρ=|Q1(x,t)|2?|Q1(x=±∞,t)|2,可以獲得磁怪波的磁振子密度分布關系: 為了進一步闡釋磁怪波的產生機制, 還需要關心的是怪波如何使磁振子和能量從背景向中心積聚, 這時需要再引入新的函數, 即積聚和耗散率來進行說明: 通過復雜的計算可以得到 這說明了在不同的自旋極化電流下怪波和背景之間的交換(圖5).根據方程(12), 可知自旋極化電流能夠調控磁孤子積聚和耗散率, 并且臨界電流為AJc=2kc.在臨界電流以下, 磁振子的交換隨著電流的增加而降低; 在臨界電流以上, 磁振子的交換隨著電流的增加而增加 (圖5(f)).從圖5(a)到圖5(e)可以看出, 自旋極化電流使怪波和背景的磁振子交換不同導致了磁怪波對于 (x,t) 空間方向的不同.當AJc=2kc時, 磁振子的空間積聚 (或者耗散)達到最大(圖5(f)).通過計算 發現: 當t<0 時, 背景中的磁振子向中間積聚; 當t=0, 怪波的臨界峰值出現; 同理, 當t>0 , 波峰中的磁振子開始向背景轉移, 波峰逐漸衰減.最后磁怪波完全消失, 這也就證明了磁怪波僅僅是一個在時間和空間上的震蕩, 充分體現了一個不穩定動力學過程的特性. 最后, 如何在實驗中探測到這種呼吸子和怪波是非常有趣的.囚禁在光格子中的玻色-愛因斯坦凝聚體可以具有鐵磁性, 即玻色鐵磁[63?65], 這種情況下m3分量的平均值可以從直接測量自旋磁量子數為+1和–1的塞曼子能級的粒子數之差來實現.這意味著對于磁呼吸子解, 存在時間或空間周期性的粒子數, 而對于怪波則粒子群為不均勻的.對于費米子鐵磁體, 電流通過鐵磁體時, 其電阻受磁矩取向的強烈影響.因此, 磁呼吸子解會使磁性層中的電阻發生周期性變化, 而怪波情況下, 應該會出現瞬時電阻的急劇變化. 圖5 (a)?(e)不同電流值激發怪波在區域 ( x,t) 的分布圖[53], 電流從 0 到 0.8, 間隔為 0.2; (f)不同電流怪波形成時的圖形, 插圖為磁振子積聚的最大時情況.臨界電流 AJ=2kc , 其它參數Ac=kc=0.2Fig.5.(a)?(e) The formation region in space ( x,t) for magnetic rogue wave with different current[53].The parameter A J ranges form 0 to 0.8 in 0.2 steps; (f) The nonuniform exchange of magnons between rogue wave and background for the different spin current.The inset figure in (f) denotes the maximal accumulation (or dissipation) process for the critical current value AJ=2kc .Other parameters are Ac=kc=0.2 . 綜上所述, 本文研究了自旋轉移力矩激發下的各向同性和單軸各向異性的鐵磁體的磁化動力學過程.首先在各向同性系統中得到了Akhmediev呼吸子、Kuznetsov-Ma孤子和怪波的精確的表達式.根據臨界條件分別分析了調制不穩定過程、周期化過程和磁怪波.這些結果對探測玻色子和費米子鐵磁體的非線性激發有一定的指導意義.然后對單軸各向異性的磁怪波進行分析發現, 能量和磁振子向中心位置的積聚對帶有強呼吸子特點的怪波的產生起主要作用, 且怪波具有暫時性和局域性.它和背景間的能量與磁振子的交換可以通過自旋極化電流調控, 并且在臨界值以上和臨界值以下自旋矩的作用完全不同.這為鐵磁系統中的調制不穩定性對非線性激發的可控性研究也提供了重要意義.

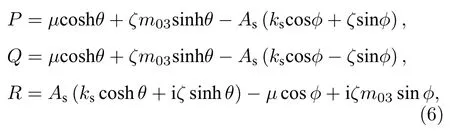

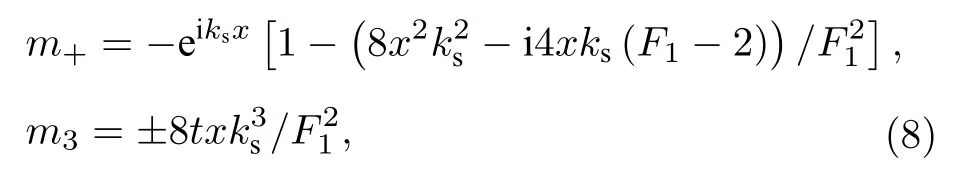

4 單軸各向異性系統中的精確怪波解
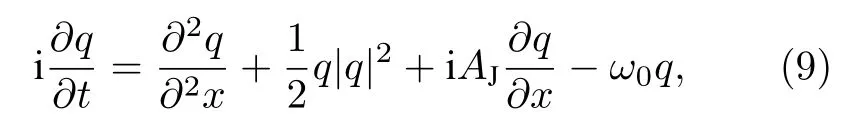

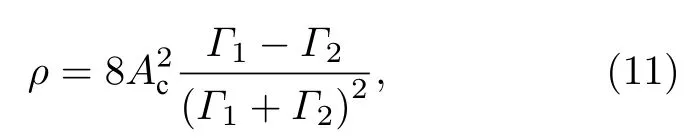
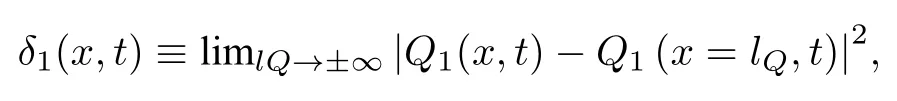
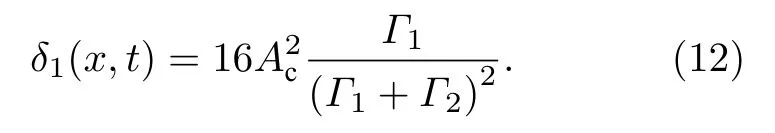
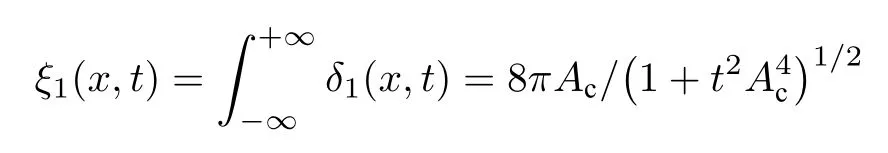
5 結 論

