基于不同破壞準則的混凝土凍融雙軸受壓破壞模型研究
劉苗苗,彭 剛,程卓群,孫尚鵬,王 普
(三峽大學土木與建筑學院,湖北 宜昌 443002)
0 引 言
混凝土的凍融劣化程度會降低其強度,進一步影響其結構的力學性能[1]。混凝土構筑物在高寒地區不可避免的會受到水、溫度、地震等環境因素的影響和車輛、波浪等沖擊荷載的作用,因此要高度重視對混凝土凍融破壞性能的研究。Shang H[1]研究表明混凝土經凍融循環后在雙軸壓荷載情況下的強度和彈性模量隨著凍融循環次數的增加而降低,應變隨著凍融循環次數增加而增大;李家正[2]研究了凍融循環過程混凝土性能的劣化特征,探討了不同測試手段對不同老化特性的敏感性;宋玉普[3]分析了雙軸拉-壓極限強度隨凍融循環次數的變化規律,并在主應力空間和八面體應力空間建立了同時考慮凍融循環次數和拉壓比的破壞準則;王海濤[4]研究了不同應變速率下全級配混凝土的單軸動態極限抗壓強度、應力-應變關系曲線,建立了綜合考慮凍融循環次數與應變速率影響的統一破壞準則;羅小勇[5]建立了不同預壓應力下混凝土抗凍預測模型,通過計算對比,證明該模型具有一定的工程價值;曹大富[6]提出了凍融循環后受壓性能的計算公式以及適用于立方體抗壓強度為20~50MPa的凍融循環作用下混凝土的應力-應變全曲線方程,并將曲線控制參數與相對動彈性模量和混凝土等級建立關系;張眾[7]建立了以應力比和凍融循環次數為連續變量的破壞準則,反算了3個主壓應力方向峰值應力點處的等效單軸應變,得到了凍融后普通混凝土雙軸等效單軸應變本構模型。這些研究主要集中于混凝土單軸凍融劣化的力學試驗和理論研究,但是工程實際中的混凝土結構又往往處于復雜應力狀態。因此,本文基于3個經典的靜態破壞準則(Ottosen準則、Bresler-Pister準則、Kupfer-Gerstle準則)建立混凝土凍融雙軸受壓破壞模型,并驗證模型的適用性。

表2 凍融混凝土在不同側壓下的峰值應力和峰值應變
1 試驗設計
1.1 試驗制備
根據JGJ55—2011《普通混凝土配合比設計規程》和DL/T5330—2015《水工混凝土配合比設計規程》,試塊混凝土按C30強度等級進行配合比設計,材料用量見表1。水泥采用P.O 42.5普通硅酸鹽水泥,細骨料選用中砂,粗骨料為粒徑5~40 mm的連續級配碎石。對試件邊長為300 mm的立方體混凝土進行鋼模澆筑、振搗密實、試件表面抹平后,室溫放置24 h拆模,再放入標準養護室養護28 d。

表1 單位體積混凝土材料用量 kg
1.2 凍融循環
本文采用的凍融設備為TR-TSDRSL凍融儀[8],凍融循環一次的時間為14~16 h左右,其中凍結時間為8~9 h,融化時間為6~7 h。將飽和完成的試件盒放入凍融箱內,采用快凍法進行3種次數(0,20,40)的凍融循環試驗,試件中心溫度控制在(-15±2)℃到(8±2)℃之間。
1.3 試驗過程
(1)試件裝樣。將置于墊板上的試件對中,然后布置試件的豎向加載板和側向傳力板,再將小車推入加載框架內,調整豎向傳力柱的位置使之與加載板至對中。
(2)預加載。利用移動和移動轉換指令分別使試件豎向、側向預加載至20 kN,保證試件與加載板之間充分接觸。
(3)正式加載。檢查并確認各項參數,利用移動轉換命令中的變形控制方式進行操控,試驗設計的側壓應力為0、0.06fc、0.12fc、0.18fc、0.24fc(本文試驗值為fc=33.33 MPa),以加載速率為10-5/s至試件完全破壞,保存數據。
1.4 試驗分析
按照上述試驗過程,本文測得凍融劣化混凝土在不同凍融次數和不同測壓下的峰值應力和峰值應變見表2。由表2可知,①相同凍融次數混凝土的峰值應力隨著側壓的增大而增大,而其峰值應變隨側壓的增大呈現出先增后減的趨勢;②凍融劣化次數影響了側壓對混凝土峰值應力和峰值應變的增益作用,即凍融次數較少時,混凝土峰值應力和峰值應變隨側壓而增大的增幅較小,凍融次數較多時,峰值應力隨側壓而增大的增幅較大;③相同側應力作用下,混凝土峰值應力隨凍融次數的增加而降低;④凍融次數越多的混凝土在不同側壓下的峰值應變變化幅度越大。
2 混凝土凍融雙軸受壓破壞模型
根據各種經典破壞準則的適用范圍、與試驗結果的吻合程度以及理論破壞包絡面的合理性選取3個經典的靜態破壞準則(Ottosen準則、Bresler-Pister準則以及Kupfer-Gerstle準則)作為研究基礎,考慮凍融劣化的影響,建立靜態混凝土凍融雙軸受壓破壞模型并對比分析擬合效果。
由于凍融劣化后的混凝土力學性能發生了很大變化,假定經凍融劣化后混凝土的靜態雙軸受壓破壞曲線與常態混凝土呈現一定的相似性,根據已有的常態混凝土雙軸破壞準則為參照進行凍融劣化混凝土模型分析,選取Ottosen準則、Bresler-Pister準則和Kupfer-Gerstle準則模型作為研究對象,在模型中主要考慮宋玉普在文獻[10]中描述混凝土的靜態單軸抗壓強度與凍融次數呈線性關系,即
fc,N=d+eN
(1)
式中,fc,N為凍融N次的混凝土單軸抗壓強度;d、e為混凝土單軸抗壓的凍融參數,根據試驗數據得到,d=0.979 2,e=-0.008 5。
2.1 基于Ottosen準則的混凝土凍融雙軸受壓破壞模型
Ottosen準則[12]作為應用范圍廣泛且被引入國外多種規范的經典破壞準則,能夠較好地描述材料破壞包絡面的幾何特征,其在主應力空間上的表達式為
(2)
(3)
式中,a、b分別為混凝土凍融雙軸壓參數,見表3;σ2為側向壓應力;σ3為豎向壓縮至破壞過程中的峰值應力;fc為常態混凝土試塊(試塊尺寸為300 mm×300 mm×300 mm)靜態加載(應變速率為10-5/s)時的單軸抗壓極限強度,本文試驗值為fc=33.33 MPa。

表3 基于Ottosen準則的混凝土凍融雙軸受壓破壞模型參數
本文凍融混凝土屬于雙向受力狀態,即σ1=0,根據上述假定公式(1),基于Ottosen準則的混凝土凍融雙軸受壓破壞模型可簡化為:
(4)
式中,k1、k2分別為擬合參數,見表3。
采用基于Ottosen準則的混凝土凍融雙軸受壓破壞模型對凍融0、20、40次混凝土的雙軸壓縮數據進行擬合,擬合參數見表3,理論曲線與樣本點的對比見圖1。本文圖例中樣本點為試驗所得,“DR-*”表示“凍融*次”。擬合過程中發現:①對于任何凍融次數的混凝土而言,偏平面包絡線大小和形狀控制參數k2均可為1,因此原始表達式可稍作簡化;②雖然從曲線和數據的對比來看,擬合效果尚可,但是由于該隱函數過于復雜,參數的初始賦值對曲線形狀的影響較大,且參數多為復數,即使將k2用1替換之后得到的參數仍然存在復數,不便于實際應用。
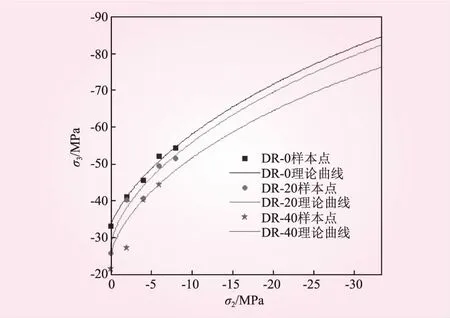
圖1 基于Ottosen準則的混凝土凍融雙軸受壓破壞模型與樣本點對比
2.2 基于Bresler-Pister準則的混凝土凍融雙軸受壓破壞模型
Bresler-Pister準則[13]是八面體剪應力系列強度理論之一,該公式是基于大量試驗數據的經驗公式。原始表達式為
(5)
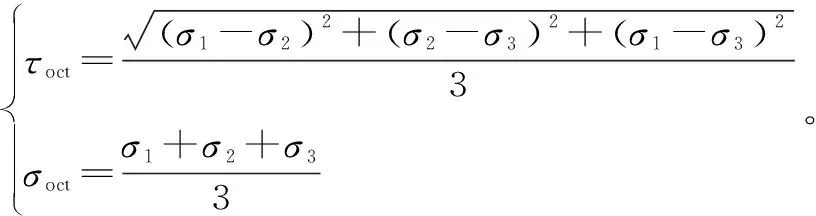
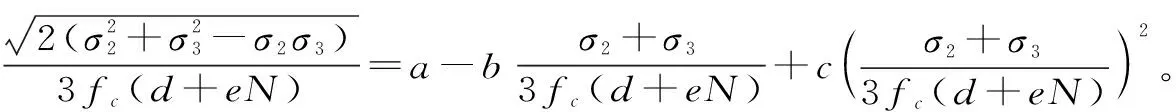
采用基于Bresler-Pister準則的混凝土凍融雙軸受壓破壞模型對凍融0、20、40次混凝土的雙軸壓縮數據進行擬合,結果見表4和圖2。在擬合分析過程中發現:①無論怎樣調整參數初始值,對應的b值都不會改變,但是現有結果顯示其與凍融次數無明顯關系;②參數a、c受初始值的影響較大,由于數據較少,看不出其與凍融次數之間的關系。
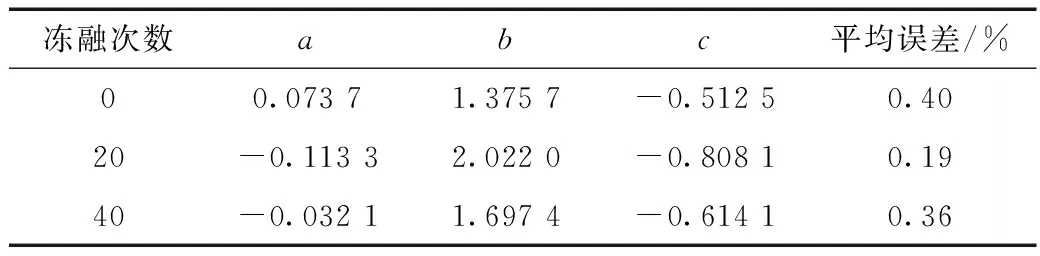
表4 基于Bresler-Pister準則的混凝土凍融雙軸受壓破壞模型參數
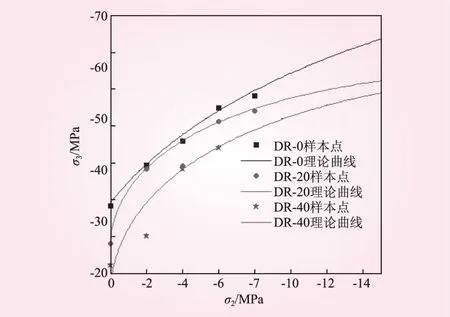
圖2 基于Bresler-Pister準則的混凝土凍融雙軸受壓破壞模型與樣本點對比
2.3 基于Kupfer-Gerstle準則的混凝土凍融雙軸受壓破壞模型
Kupfer-Gerstle準則(簡稱K-G準則)作為常用的二維結構在主應力空間上的破壞準則,經修正后被納入歐洲規范,且國內許多學者的研究中也借鑒了該準則[14-15],其原始表達式為
(6)
式中,a、b為待定系數,因材料特性而定。
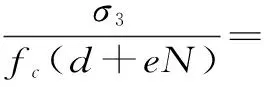
采用基于K-G準則的混凝土凍融雙軸受壓破壞模型對凍融0、20、40次混凝土的雙軸壓縮試驗數據進行擬合,擬合參數及相關性系數見表5和圖3。
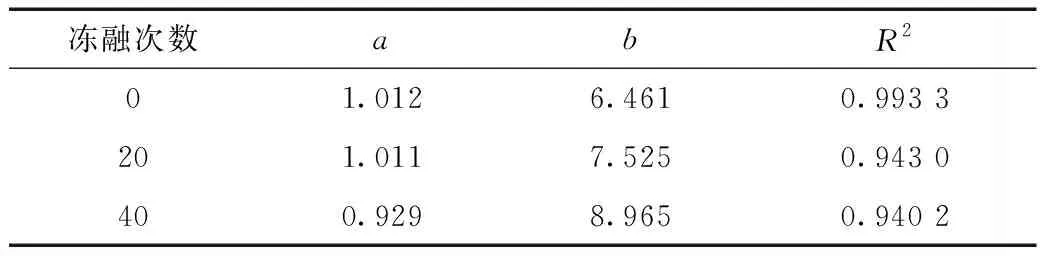
表5 基于K-G準則的混凝土凍融雙軸受壓破壞模型參數
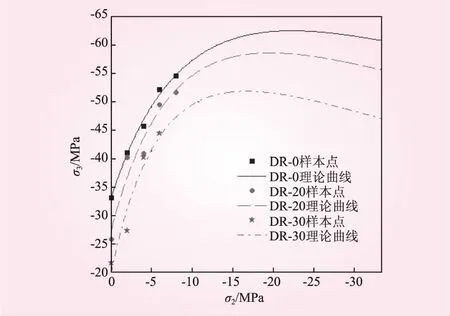
圖3 基于K-G準則的混凝土凍融雙軸受壓破壞模型與樣本點對比
2.4 K-G準則的改進
由表5可知隨著凍融次數的增大,參數a在0.1附近變化很小,可假定a不受凍融次數的影響,將其取為1;而參數b變化很明顯,故將參數b作為與凍融相關的參數。通過數據擬合,可以發現,參數b與凍融次數N之間近似存在指數關系,即
b=b1eb2N
(7)
式中,b1、b2為凍融對混凝土雙軸受壓強度的影響參數。通過數據擬合分析,b1=6.428,b2=0.008 25。
因此,在常態混凝土單軸抗壓強度fc已知的情況下,可以得到任意凍融循環次數后的混凝土雙軸受壓破壞曲線。
圖4為根據改進后的K-G破壞準則的理論曲線與樣本點之間的對比。通過計算,得到凍融0、20、40次的樣本點與破壞準則曲線之間的平均誤差分別為1.53%、4.76%、5.34%,可見基于改進K-G準則對于本文的試驗數據具有較好的精度。

表6 粉煤灰陶粒混凝土極限抗壓強度[16] MPa
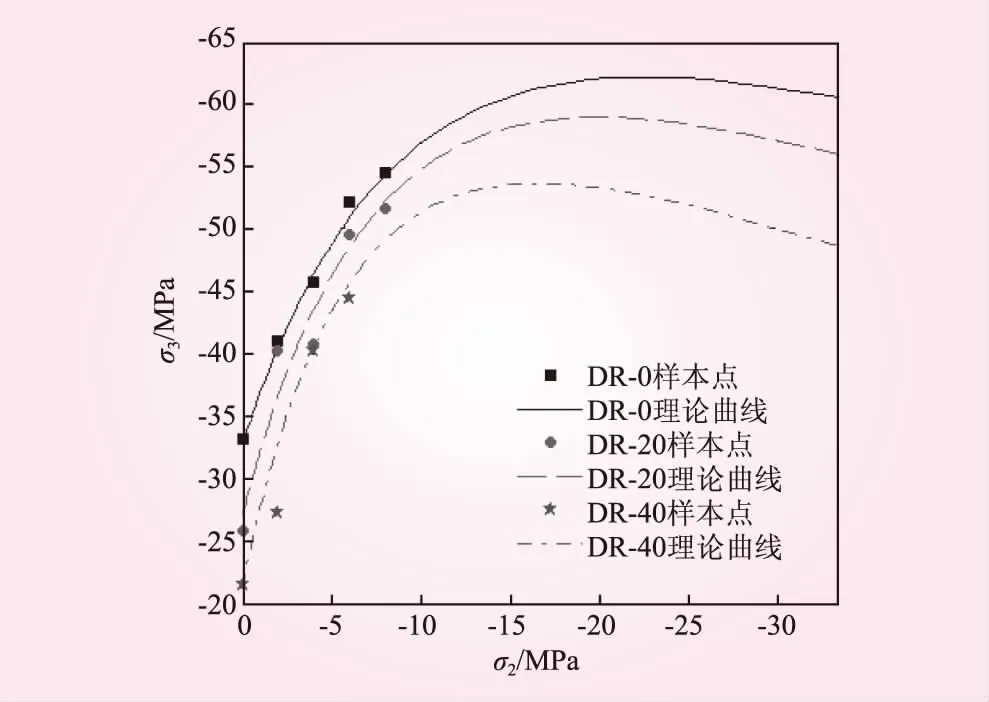
圖4 基于改進-G準則的混凝土凍融雙軸受壓破壞模型與樣本點對比
3 基于改進K-G準則的混凝土凍融雙軸受壓破壞模型的驗證
為驗證基于改進K-G準則所建模型的適用性,引用文獻[16]中對邊長100 mm的粉煤灰陶粒混凝土進行了凍融后的混凝土雙向受壓試驗,表6為文獻[16]的試驗數據,將數據代入新建模型進行研究。
考慮凍融循環的單軸強度準則為fc,N/fc=0.979 1-0.002 247N,擬合得到混凝土參數b與凍融次數之間的關系滿足b=3.356e0.001 97N。因此,針對文獻[16]里的粉煤灰陶粒混凝土,對應于本文基于改進K-G準則建立的模型參數分別為d=0.9791,e=-0.002 247,b1=3.356,b2=0.001 97,樣本點與模型的對比見圖5。
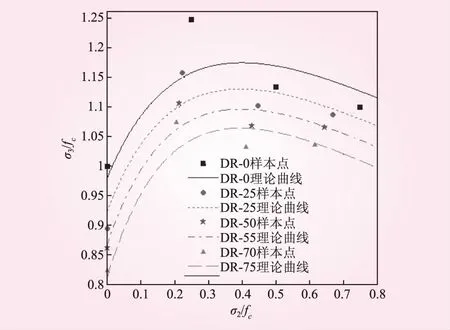
圖5 試驗數據[16]與改進K-G模型試驗結果對比
基于改進K-G準則的模型能夠比較好地描述混凝土雙軸受壓強度變化規律,該模型的參數與材料組成和凍融程度均相關,并且模型直接將混凝土凍融單軸強度準則直接應用了起來,即本文模型可用于混凝土凍融單軸、雙軸受壓破壞計算。
4 結 論
本文對不同凍融循環次數加載下混凝土進行了力學性能分析,得到凍融劣化后的混凝土在不同側壓力下的峰值應力和峰值應變的變化規律。為進一步分析其破壞機理,考慮混凝土凍融劣化后的雙軸破壞包絡面與常態混凝土具有一定的相似性,并假定單軸抗壓強度隨凍融次數呈線性遞減規律,建立了基于Ottosen準則、Bresler-Pister準則以及Kupfer-Gerstle準則的凍融劣化混凝土靜態雙軸受壓破壞模型,得到以下結論:
(1)基于Ottosen準則建立的模型雖然能夠很好地描述側壓力為范圍內的雙軸壓縮變化規律,但其參數值太復雜,不便于應用。
(2)基于Bresler-Pister準則和Kupfer-Gerstle準則建立的模型均可以較好的描述0~0.24fc側壓范圍內的凍融劣化混凝土靜態雙軸受壓強度破壞規律。
(3)將基于改進后的Kupfer-Gerstle準則建立的凍融雙軸受壓模型與其他文獻混凝土在凍融劣化下的雙軸受壓數據作對比,可知新模型的計算精確度較高,具有較強的適用性,并且可以應用于混凝土凍融單軸、雙軸受壓破壞計算。

