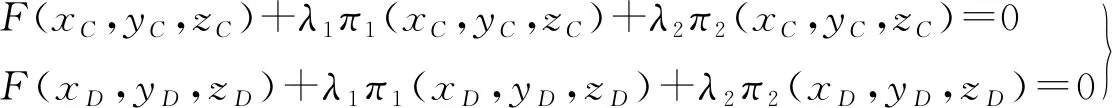過異面四點確定球面方程的策略分析

王成強

(成都師范學院 數學學院，四川 成都 611130)

引言

“解析幾何”是大學數學的重要知識模塊，對培養學生的空間想象能力、抽象思維能力、科學計算能力等都大有裨益[1-2]. 二次曲面理論是大學數學解析幾何知識模塊的重難點，每屆中國大學生數學競賽都會涉及對二次曲面理論的考查[3]. 中國大學數學競賽每年舉辦一屆，試題分為數學專業類與非數學專業類，它們的命題角度新穎，趣味性濃郁，創新性強，具有極高的研究價值[3-4]. 2011年舉辦的第三屆中國大學生數學競賽預賽試卷的第一題涉及求解一類特殊二次曲面，即球面方程的問題，其完整表述如下：

球面是一類高度對稱的二次曲面，其定義可簡略表述為空間中到定點的距離等于定值的點的全體. 球面是高中階段所學的圓周理論的延伸與拓展，而眾所周知的是，后者具有豐富的性質，是高中階段數學學習的重難點，因空間幾何的復雜性，空間球面的性質更加豐富，其學習或者相關問題的解答需要更豐富的空間想象能力. 本文旨在以問題(*)為基礎，探究空間中過異面四點確定球面方程的策略.

1 三維空間中過異面四點確定球面方程的策略

方法1利用“列標準方程 + 求幾何參數”的方法確定球面的方程

設球面S的標準方程為(x-x0)2+(y-y0)2+(z-z0)2=r2. 將點A、B、C、D的坐標代入此方程，得

可發現該方程組等價于

由Cramer法則，得

進一步，還有：

r2=(1-x0)2+(2-y0)2+(7-z0)2=(1-1)2+(2+1)2+(7-3)2=25

綜上，球面S的標準方程為：

(x-1)2+(y+1)2+(z-32)=25

方法2利用球面的幾何實質確定其方程

設球面的球心的坐標為(x0,y0,z0)，按球面的定義，點A、B、C、D到球心的距離相等，即

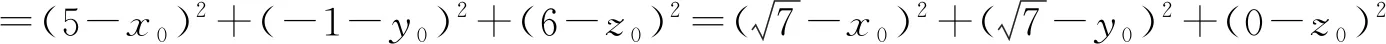
與方法1類似，經整理與化簡可得方程組

仿照方法1，利用Cramer法則，經計算可得(x0,y0,z0)=(1，-1，3). 于是，球面S的標準方程為

(x-1)2+(y+1)2+(z-3)2=(x-x0)2+(y-y0)2+(z-z0)2=(1-1)2+(2+1)2+(7-3)2=25

方法3利用球心的特殊幾何位置屬性確定球面的方程

球面S的球心同時位于下列兩條空間直線上：

與

換言之，球面S的球心坐標(x0,y0,z0)滿足方程組

仿照方法1，利用Cramer法則，經計算可得(x0,y0,z0)=(1,-1,3). 仿照方法2可完成余下的步驟.

方法4利用球面簇確定球面的方程

以AB為直徑的球面方程為

(x-1)(x-4)+(y-2)(y-3)+(z-7)(z-3)=0

或者

x2+y2+z2-5x-5y-10z+31=0

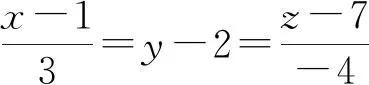
x2+y2+z2-5x-5y-10z+31+λ1(x-3y+5)+λ2(4y+z-15)=0

將點C、D的坐標代入上述方程，得

由Cramer法則，得

于是，球面S的方程為

x2+y2+z2-5x-5y-10z+31+3(x-3y+5)+4(4y+z-15)=x2+y2+z2-2x+2y-6z-14=(x-1)2+(y+1)2+(z-3)2-25=0

即球面S的標準方程為：(x-1)2+(y+1)2+(z-3)2=25

方法5利用“列一般方程+求系數”的方法確定球面的方程

設所求球面的一般方程為x2+y2+z2+ux+vy+wz+f=0. 代入A、B、C、D的坐標，得到方程組

由Cramer法則，得

于是，球面S的標準方程為：(x-1)2+(y+1)2+(z-3)2=25

注1一般地，仿照方法5，可得到三維空間中過異面的四點P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)的球面的方程

經整理，得

方法6利用公式確定球面的方程

經化簡整理，有

即球面S的標準方程為：(x-1)2+(y+1)2+(z-3)2=25

2 過空間異面四點確定球面方程與過平面不共線三點確定圓周方程

過空間異面四點確定球面方程與過平面不共線三點確定圓周方程的過程相似.事實上，前文提出的過空間異面四點確定球面方程的六種方法中的思路都適用于過平面不共線三點確定圓周方程. 方法1與方法5可籠統歸為方程思想，這類方法在確定平面圓周方程方面有重要應用.例如，為確定過平面不共線三點A(x1，y1)、B(x2，y2)、C(x3，y3)的圓周的方程，應先列出該圓周的標準方程(x-x0)2+(y-y0)2=r2(x0、y0、r待定)或者一般方程x2+y2+2Dx+2Ey+F=0(D、E、F待定)，然后代入點A、B、C的坐標并求出待定參數的值，最后回代參數的值就可得到圓周的方程.方法6的思路(詳見注1)也可用于確定平面圓周的方程.事實上，有下述結論成立：過不共線三點A(x1，y1)、B(x2，y2)、C(x3，y3)的圓周方程為

與平面圓周相比，空間球面的幾何結構更復雜，幾何性質更豐富.例如，在方法3中，為確定過空間異面四點A、B、C、D的球面方程，先利用球心在空間直線段AB、AC、AD、BC、BD、CD的中垂面上這一性質以確定球心的坐標，再計算出點A(B、C或D)到球心的距離，此即為球面半徑，綜合這兩方面信息就可寫出球面的方程. 方法3的思路也可用于確定過平面不共線三點A、B、C的圓周的方程：先利用圓心在平面直線段AB、AC、BC的中垂線上這一性質確定圓心的坐標，再計算出點A(B或C)到圓心的距離，此即為圓周半徑，綜合這兩方面信息就可寫出圓周的方程. 又如，在方法4中，為確定過空間異面四點A、B、C、D的球面方程，先確定出以A、B為對徑點的球面方程F(x,y,z)=0，再確定出平面ABC的方程π1(x,y,z)=0與ABD的方程π2(x,y,z)=0，之后假設球面S的方程為F(x,y,z)+λ1π1(x,y,z)+λ2π2(x,y,z)=0，最后代入C、D找出等量關系，列方程解方程確定出待定參數λ1與λ2，回代參數λ1與λ2的值便得出球面S的方程.方法4的思路在確定平面圓周方程中也有重要應用.為確定過平面不共線三點A、B、C的圓周方程，可先確定以A、B為對徑點的圓周的方程G(x,y)=0及直線AB的方程L(x,y)=0，然后設出圓周的方程G(x,y)+λL(x,y)=0，并通過代入點C的坐標求出λ的值，最后回代λ的值便得到圓周的方程.

經前述分析可發現，過空間異面四點確定球面方程與過平面不共線三點確定圓方程周方程，兩者的思路與過程都緊密相關，每種用以確定平面圓周方程的思路都可用以探究確定空間球面方程.但是，與過平面不共線三點確定圓方程周相比，過空間異面四點確定球面方程則需要更豐富的空間想象能力與較強的科學計算能力.

3 結語