裝配式T型鋼空腹夾層板組合樓蓋受力性能研究

謝小華，呂曉勇，曹明遠，蔡 勇

（1.長沙市望城區建設工程質量安全管理辦公室，湖南 長沙 410200；2.中南大學 土木工程學院，湖南 長沙 410075）

1 研究背景

裝配式T型鋼空腹夾層板組合樓蓋[1-2]，是在鋼筋混凝土空腹夾層板樓蓋結構基礎之上提出的一種新型組合樓蓋。它是先由車間制作的T型鋼上、下肋組成“雙層井字”拼裝單元，再運往施工現場；然后在上、下肋彎矩最小處，通過高強螺栓等強連接，并且在上面澆筑一層鋼筋混凝土板，通過栓釘與上肋T型鋼梁連接的一種新型組合樓蓋。

較多科研工作者對裝配式T型鋼空腹夾層板組合樓蓋的受力性能進行了研究。如魏艷輝等[2]研究了在上、下弦反彎點處裝配整體式空腹夾層板，并對其進行了分級加載靜力試驗，且對建立的相對應的有限元模型進行了模擬對比分析，得出了結構的整體剛度較好、荷載傳遞分配合理可靠，結構具有較高的抗彎承載力的結論。楊期柱、張瑞鵬等[3-5]對大跨度空腹夾層板樓蓋的受力性能和設計方法進行了系統研究，結果表明，空腹夾層板鋼肋處于拉彎、壓彎受力狀態，樓蓋線性屈曲時以整體失穩為主，穩定性較好。吳幫等[6-7]對型鋼混凝土組合空腹夾層板及U形鋼板-混凝土組合空腹夾層板樓蓋的受力性能和設計方法進行了研究，結果表明，應用現有實用計算方法進行設計，其結果安全、可靠，且組合夾層板的整體性能較好，抗震性能良好。姚玲等[8]對混凝土空腹夾層板靜力性能進行了有限元參數分析，結果表明，結構內力分布與空腹網架類似，但是剪力鍵變形時表現出整體轉動的特點。

本文擬在已有研究成果的基礎上，進一步對裝配式T型鋼空腹夾層板組合樓蓋的理論計算公式進行推導，并利用ABAQUS有限元分析軟件建立四邊簡支承裝配式T型鋼空腹夾層板組合樓蓋的有限元模型，探討各影響因素的改變對該組合樓蓋抗彎承載力的影響程度，以期為裝配式T型鋼空腹夾層板組合樓蓋的設計提供理論參考依據。

2 理論計算公式

2.1 空腹夾層板內力計算

本研究將鋼空腹夾層板連續化分析為擬夾層板，其計算模型和基本假定參考文獻[9-10]；上、下表層平面剛度以及空腹夾層板等效剪切剛度參考文獻[3，11-12]，取擬夾層板的上表層為計算參考面，并選用擬夾層板的3個廣義位移w、φx、φy，其基本的方程式參考文獻[7，13-15]。矩形平面的空腹夾層板在周邊簡支條件下，根據簡支邊矩形薄板的納維解法，采用重三角級數求解基本方程組，在求得鋼空腹夾層板整體內力之后，就可以根據單位寬度擬夾層板上的內力相等原則，求出混凝土板、上肋、下肋以及剪力鍵各類構件所受的內力，它們的計算公式參考文獻[7，13-15]。

2.2 空腹夾層板組合樓蓋設計計算方法

空腹夾層板上表層中混凝土薄板會分擔一部分的平面力，并且可以考慮薄板的薄膜效應，因此，在設計計算中，上層混凝土板在承載力和剛度這兩個方面的貢獻都應予以考慮。

上部鋼結構T型鋼梁和混凝土板通過T型鋼梁上的栓釘連接成整體，因而按組合結構的組合構件進行截面承載力設計比較合理；下肋的實際受力狀態為拉彎，故將下肋構件按拉彎構件進行截面承載力設計，這樣的設計符合鋼空腹夾層板組合樓蓋結構的實際受力狀態。將2.1節中計算得到的四邊簡支裝配式T型鋼空腹夾層板組合樓蓋截面的整體彎矩，按上、下肋構件截面的剛度進行分配，然后分別進行設計計算。

2.2.1 上肋組合構件的設計計算

分配到上肋組合構件上的彎矩為

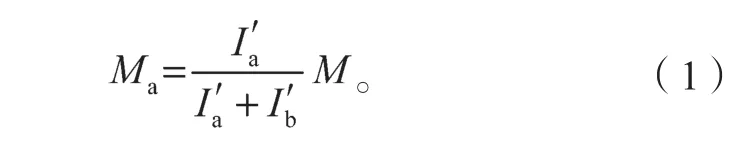
式中：M為整個截面上的彎矩；

Ma為分配到上肋組合構件上的彎矩；

I′a為上肋組合構件的慣性矩；

I′b為下肋鋼構件的慣性矩。

將上弦鋼肋按組合構件設計進行計算，分兩種情況考慮。

1）完全抗剪連接

抗彎承載力由控制截面所能承擔的最大彎矩決定。計算截面的塑性承載力時，需要先做如下假定：

i）在承載力極限狀態，鋼梁和混凝土翼緣板之間的剪力可以通過抗剪連接件可靠地進行傳遞；

ii）鋼梁和混凝土之間沒有滑移；

iii）忽略混凝土的抗拉作用；

iv）假定平截面適用于其截面應變。

當Af≤behc1fc（其中，A為T型鋼的截面面積，f為屈服強度，be為混凝土翼板有效寬度，hc1為混凝土有效高度，fc為抗壓強度），即組合截面塑性中和軸位于混凝土翼緣板內時，其計算簡圖如圖1所示。

圖1 塑性中和軸在混凝土上翼板內的應力計算簡圖Fig.1 Stress calculation map of plastic neutralization axis in concrete upper flange plate

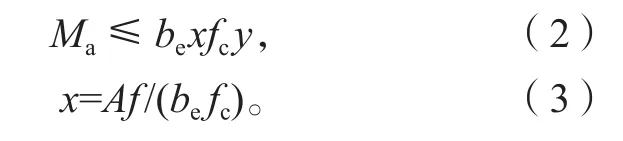
式（2）（3）中：x為混凝土翼緣板的受壓區高度；

y為兩種不同材料（T型鋼和混凝土受壓區）截面應力合力之間的距離。

當Af>behc1fc，即組合截面塑性中和軸位于T型鋼截面內時，其計算簡圖如圖2所示。

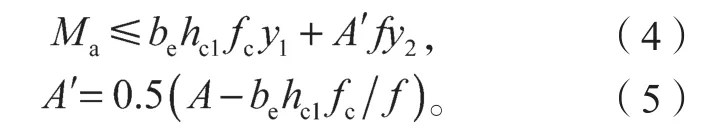
式（4）（5）中：A′為T型鋼受壓區截面面積；

y1為兩種不同材料（T型鋼受拉區和混凝土翼緣板）截面應力合力之間的距離；

y2為T型鋼受拉區和其受壓區截面應力合力之間的距離。

2）部分抗剪連接

部分抗剪連接時，組合構件的極限抗彎承載力計算簡圖如圖3所示。

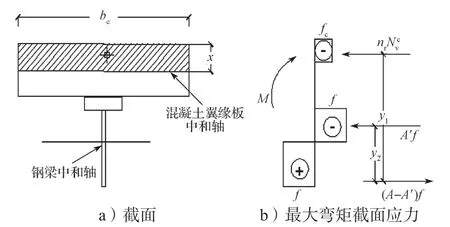
圖3 部分抗剪連接構件的極限抗彎承載力計算簡圖Fig.3 Calculation sketch of ultimate flexural bearing capacity of partial shear connection

部分抗剪連接情況下，對組合構件的極限抗彎承載力進行計算時，做如下假定：

i）抗剪連接件必須有較好的塑性變形能力；

ii）計算截面的應力呈矩形分布，混凝土翼緣板中的壓應力達到其抗壓強度fc，T型鋼的拉、壓應力分別達到屈服強度f；

iii）抗剪連接件所傳遞的縱向剪力之和就是混凝土翼緣板中的壓力；

iv）不考慮混凝土的抗拉作用。

式（6）～（8）中：nr為抗剪連接件個數，取計算截面兩側剪跨區內數量較小的；

2.2.2 下肋鋼構件的設計計算

下肋鋼構件按拉彎構件設計，其中下肋鋼構件的彎矩按剛度分配，可得

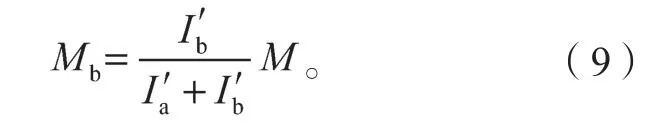
式中，Mb為分配到下肋組合構件上的彎矩。

下肋鋼構件軸力如下：

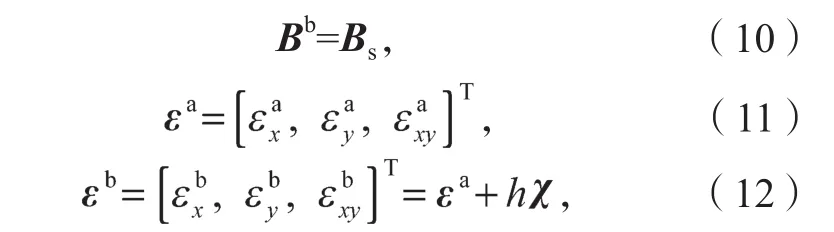
式（10）～（12）中：Bb為下表層的薄膜剛度矩陣；Bs為下表層等效薄膜剛度；εa、εb分別為上表層的平面應變、下表層的平面應變；h為上、下弦層構件截面形心之間的距離；χ為擬夾層板的彎曲應變，且

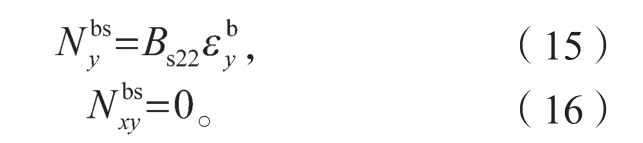
求得下肋等效薄膜內力之后，可根據網格尺寸反求出鋼肋構件承受的x、y方向的軸力：

此時，將下弦鋼肋按照在軸力Nbs和彎矩Mb作用下的拉彎構件計算：

式中：An為凈截面面積；

Wnx、Wny分別為對x軸、y軸凈截面抵抗矩；

γx、γy分別為對x軸、y軸凈截面抵抗矩系數。

3 組合樓蓋有限元模型驗證

文獻[2]對上、下弦反彎點處裝配式鋼空腹夾層板做了分級加載靜力試驗研究。本研究以ABAQUS有限元分析軟件為工具，建立了與文獻[2]試驗相一致的有限元模型，如圖4所示。

圖4 與文獻[2]中試驗對應的有限元分析模型Fig.4 Finite element analysis model corresponding to the experiment in reference[2]

所建立的有限元模型中，用4節點減縮積分格式的殼單元（S4R）模擬T型鋼，沿殼單元的厚度方向采用9節點的Simpson積分，以滿足計算精度的要求。用8節點減縮積分格式的三維實體單元（C3D8R）模擬混凝土。有限元模擬時的邊界條件和加載方案與試驗保持一致。網格劃分上，本研究采用結構化網格劃分技術。為驗證有限元模型的可靠性和有限元建模方法的正確性，將有限元模擬的計算結果與文獻[2]中的試驗結果進行對比，部分數據對比如圖5和圖6所示。

圖5 有限元分析與試驗所得荷載-撓度曲線對比圖Fig.5 Comparison diagram of the load-deflection curves between finite element method and the test

圖6 有限元分析與試驗所得荷載-應變曲線對比圖Fig.6 Comparison diagram of the load-strain curves between finite element method and the test

由圖5和圖6可以得出，采用ABAQUS有限元模擬分析組合樓蓋得出的荷載-撓度曲線和試驗得出的荷載-撓度曲線的吻合度較高。其中，9號測點在試驗荷載下用有限元模擬得出的最大撓度為11.53 mm，與試驗實測所得的最大撓度值12.76 mm相比，誤差僅為9.64%；0號測點在試驗荷載下用有限元模擬得出的最大撓度為0.339 mm，與試驗實測所得到的最大撓度值0.321 mm相比，誤差僅為5.61%；18號測點在試驗荷載下用有限元模擬得出的最大應變為1 167，與試驗實測所得的最大應變1 123相比，誤差僅為3.92%；24號測點在試驗荷載下用有限元模擬得出的最大應變為1 150，與試驗實測所得的最大應變1 121相比，誤差僅為2.59%。

由上述分析可以得知，采用ABAQUS有限元模擬分析組合樓蓋得出的結果數據曲線與試驗所得出的吻合度較高，各測點分析結果誤差均在10%以內。說明文獻[4]中用ABAQUS有限元分析軟件所建立的上、下弦反彎點處裝配式鋼空腹夾層板組合樓蓋有限元模型是可靠的，其有限元建模方法是可行的，具有較高的精度。

4 四邊簡支裝配式鋼空腹夾層板組合樓蓋受力性能有限元分析

4.1 四邊簡支裝配式鋼空腹夾層板組合樓蓋有限元模型

用已經在前文經過可行性驗證的有限元建模方法，建立4.5 m×4.5 m的四邊簡支裝配式鋼空腹夾層板組合樓蓋有限元模型，構件的截面尺寸與文獻[2]中的一致，該ABAQUS有限元模型的單元選取、材料本構關系、接觸相互作用、網格劃分等均與上一章相同，在邊界條件上采用的是四邊簡支，即在組合樓蓋的1條邊上施加x、y、z3個方向上的位移約束，另外3條邊上僅施加z方向上的位移約束。該組合樓蓋有限元模型如圖7所示。

圖7 四邊簡支鋼空腹夾層板樓蓋有限元模型Fig.7 Finite element model for the composite floor of fourside supported steel sandwich plate

4.2 組合樓蓋抗彎承載力有限元分析

按組合樓蓋在使用過程中的實際受力形式進行加載，即在上層混凝土板面上施加均布荷載，直至加載過程中結構中有鋼梁達到其鋼材的抗拉強度進而斷裂為止（由于該組合樓蓋結構是超靜定結構，盡管有鋼梁因斷裂而退出工作，承載力仍能繼續提高，因而其荷載-撓度曲線并沒有出現下降段），分別研究下部鋼結構所用鋼材的鋼板厚度、下部鋼結構所用的鋼材牌號、上層澆筑混凝土板的厚度、上層混凝土板所用的混凝土強度等級、連接上層混凝土板與下部鋼結構的栓釘間距等影響因素的改變，對組合樓蓋抗彎承載力的影響。

4.2.1 鋼材鋼板厚度對抗彎承載力的影響

研究下部鋼結構所用鋼材的鋼板厚度對四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的影響時，分別對建立的鋼板厚度為6,7,8,10 mm 4個組合樓蓋有限元模型進行分析，其他影響因素均相同，得到的荷載-撓度曲線如圖8所示。

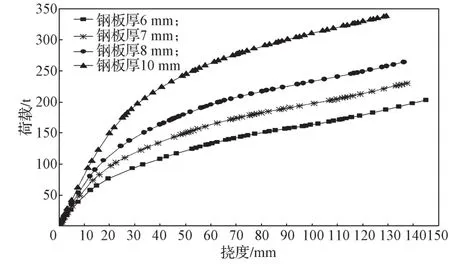
圖8 不同鋼板厚度組合樓蓋荷載-撓度曲線Fig.8 Load-deflection curves of the composite floors with different thickness of steel plate

由圖8可以看出，鋼板厚度的增加對于提高四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力具有明顯的作用。4種不同鋼板厚度的組合樓蓋模型的抗彎承載力分別為203.005,230.462,264.220,338.264 t，其抗彎承載力依次比上一鋼板厚度的提高了13.53%,14.65%,28.02%。由此可見，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著鋼板厚度的增加而提高，并且提高效果顯著。

4.2.2 鋼材強度等級對抗彎承載力的影響

為研究下部鋼結構所用鋼材的強度等級（鋼材牌號）對四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的影響，分別對建立的鋼板牌號為Q235、Q290、Q310、Q345、Q420共5個組合樓蓋的有限元模型進行分析，其他影響因素均相同，所得各模型的荷載-撓度曲線如圖9所示。

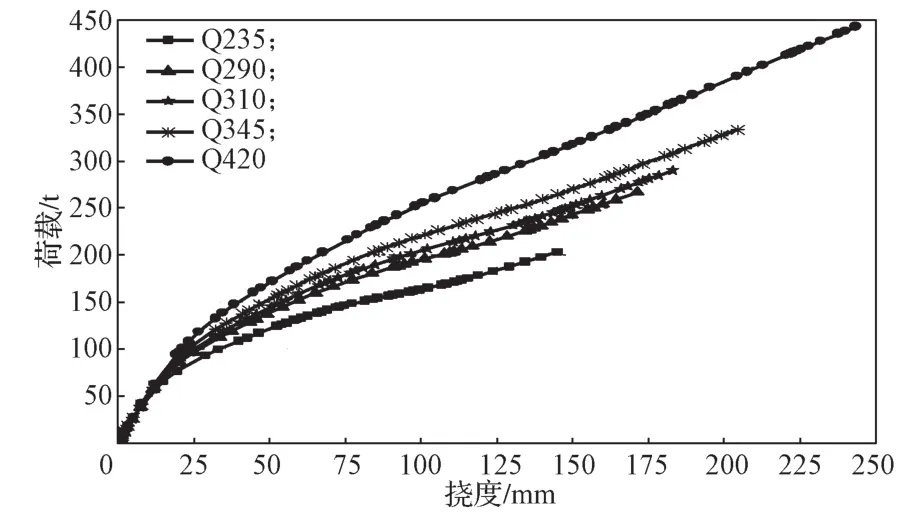
圖9 不同鋼材強度等級（鋼材牌號）的組合樓蓋荷載-撓度曲線Fig.9 Load-deflection curves of the composite floors with different grades of steel strength (steel grade)

由圖9可以看出，鋼材的強度等級（鋼材牌號）的提高，對于提高四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力具有明顯的作用。5種不同鋼材牌號組合樓蓋模型的抗彎承載力分別為203.005,266.952,289.970,333.346,443.070 t，其抗彎承載力依次比上一鋼材強度等級（鋼材牌號）的提高了31.50%,8.62%,14.96%,32.92%。由此可見，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著鋼材強度等級（鋼材牌號）的提高而提高，且提高效果顯著。在T型鋼梁與剪力鍵的連接處應力最大，各種牌號的鋼板分別達到其極限強度352.5,435,465,518,630 MPa。

4.2.3 混凝土厚度對抗彎承載力的影響

為研究上層澆筑混凝土板的厚度對四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的影響，分別對建立的混凝土板板厚度為80,90,100,110,120 mm 5個組合樓蓋有限元模型進行分析，其他影響因素均相同，得到的荷載-撓度曲線如圖10所示。

圖10 不同混凝土板厚度的組合樓蓋荷載-撓度曲線Fig.10 Load-deflection curves of the composite floors with different concrete slab thickness

由圖10可以看出，混凝土板厚度的增加對于提高四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力具有一定的作用。5個不同混凝土板厚度的組合樓蓋模型的抗彎承載力分別為176.691,192.287,203.005,222.986,243.590 t，其抗彎承載力依次比上一混凝土板厚度的提高了8.83%,5.57%,9.84%,9.24%。由此可見，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著混凝土板厚度的增加而提高，且具有一定的提高效果。在T型鋼梁與剪力鍵的連接處應力最大，鋼板達到其352.5 MPa的極限強度。

4.2.4 混凝土強度等級對抗彎承載力的影響

為研究上層澆筑混凝土板的混凝土強度等級對四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的影響，分別對建立的混凝土強度等級為C30、C40、C50、C60共4個組合樓蓋有限元模型進行分析，其他影響因素均相同，所得組合樓蓋達極限承載力的應力云圖見圖11，其荷載-撓度曲線見圖12。

圖11 組合樓蓋達到極限承載力的應力云圖Fig.11 Stress nephogram of the composite floors reaching ultimate bearing capacity

由圖11可知，在T型鋼梁與剪力鍵的連接處應力最大，鋼板達到其352.5 MPa的極限強度。

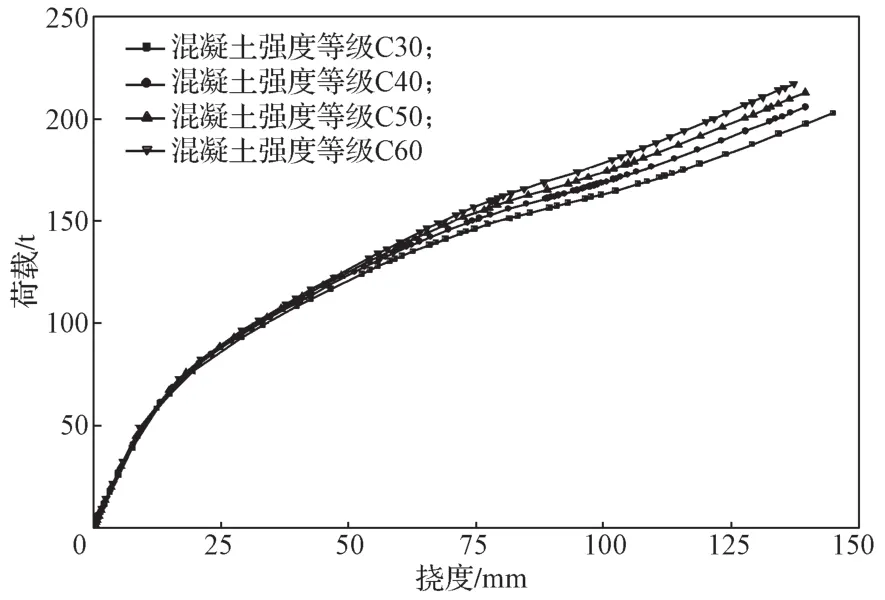
圖12 不同混凝土強度等級組合樓蓋荷載-撓度曲線Fig.12 Load-deflection curves of the floors with different concrete strength grades

由圖12可看出，上層澆筑混凝土板的混凝土強度等級增加對于提高四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的作用很小。4個不同混凝土板厚度組合樓蓋模型的抗彎承載力分別為203.005,205.858,213.113,217.338 t，其抗彎承載力依次比上一混凝土強度等級的提高了1.41%,3.52%,1.98%，由此可見，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著混凝土板的混凝土強度等級提高而提高，但提高效果有限。

4.2.5 栓釘間距對抗彎承載力的影響

為研究連接上層混凝土板與下部鋼結構的栓釘間距對四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的影響，分別對建立的栓釘間距為150,120,100,80 mm的4個組合樓蓋有限元模型進行分析，其他影響因素均相同，得到的荷載-撓度曲線如圖13所示。

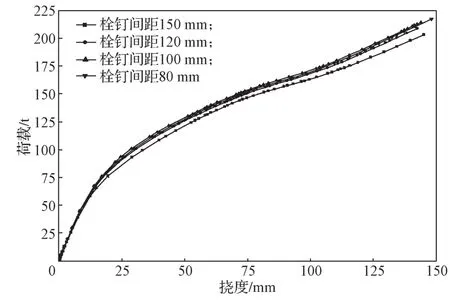
圖13 不同栓釘間距組合樓蓋荷載-撓度曲線Fig.13 Load-deflection curves of the composite floors with different spacing of studs

由圖13可以看出，栓釘間距的減小對于提高四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的作用很小。4個不同栓釘間距的組合樓蓋模型的抗彎承載力分別為203.005,208.632,214.235,21.716 t，其抗彎承載力依次比上一栓釘間距的提高了2.77%,2.69%,1.37%，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著栓釘間距的減小而提高，連接上層混凝土板與下部鋼結構的栓釘間距越小，下部鋼結構和上層混凝土板的組合效應越好，但提高效果十分有限。在T型鋼梁與剪力鍵的連接處應力最大，鋼板達到其352.5 MPa的極限強度。

5 理論計算方法驗證

以第三節所建立的4.5 m×4.5 m四邊簡支裝配式鋼空腹夾層板組合樓蓋有限元模型為算例。T型鋼和圓鋼管剪力鍵的截面尺寸參考文獻[2]中上、下弦反彎點處鋼空腹夾層板試驗中構件的截面尺寸，具體尺寸見表1。

表1 鋼構件截面尺寸Table1 Section dimensions of steel members

上層混凝土板中砼強度等級是C30，其板厚為100 mm，鋼材牌號為Q235。

計算得到上部組合構件換算截面的慣性矩為2.208 542 9×107mm4，下部鋼結構截面的慣性矩為0.665 171 2×107mm4，上、下肋截面剛度比為3.38:1。在2.0 kN/m2樓面均布荷載作用下，按上述理論公式計算得組合樓蓋跨中撓度為0.738 mm，ABAQUS有限元分析軟件得到的組合樓蓋跨中撓度值為0.817 mm，相差9.67%。ABAQUS有限元分析軟件計算得到的四邊簡支裝配式鋼空腹夾層板組合樓蓋任意截面的上部組合構件截面彎矩與下部鋼結構截面彎矩的比值約為3:1，上部組合構件截面應力與下部鋼結構截面應力的比值也約為3:1，與上、下肋截面的剛度比基本一致。因此，將組合樓蓋截面的整體彎矩按上、下肋構件截面剛度進行分配，再分別按組合構件和拉彎構件進行設計計算的方法是可行的。

6 結論

1）上部鋼結構T型鋼梁和混凝土板通過T型鋼梁上的栓釘連接成整體，按組合結構的組合構件進行截面承載力設計比較合理；下肋的實際受力狀態為拉彎，將下肋構件按拉彎構件進行截面承載力設計比較合理，這樣也符合鋼空腹夾層板組合樓蓋結構的實際受力狀態。

2）提出了將按“擬夾層板”方法計算得到的四邊簡支裝配式T型鋼空腹夾層板組合樓蓋截面的整體彎矩，按上、下肋構件截面的剛度進行分配，再將上、下肋構件分別按組合構件和拉彎構件進行設計計算的方法。并且通過相關算例與有限元模擬分析結果對比，驗證了該設計計算方法是可行的。

3）鋼板厚度的增加、鋼材強度等級（鋼材牌號）的提高、上層澆筑混凝土板厚度的增加、上層澆筑混凝土板的混凝土強度等級的提高以及連接上層混凝土板與下部鋼結構的栓釘間距的減小都會提高四邊簡支裝配式鋼空腹夾層板組合樓蓋的抗彎承載力。在影響四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力的各種因素中，鋼板厚度和鋼材強度等級（鋼材牌號）的改變對組合樓蓋的抗彎承載力的影響十分明顯；混凝土板的厚度在一定范圍內時，四邊簡支裝配式鋼空腹夾層板組合樓蓋抗彎承載力隨著混凝土板厚度的增加有較明顯的提高；而栓釘間距在滿足最小間距的要求后，其間距的改變對抗彎承載力的影響相對較小；上層澆筑混凝土板的混凝土強度等級的改變對組合樓蓋的抗彎承載力的影響則作用很小。