基于模塊度函數的加權蛋白質復合物識別算法

毛伊敏，劉銀萍

江西理工大學 信息工程學院，江西 贛州341000

1 引言

在蛋白質相互作用（Protein-Protein Interaction，PPI）網絡中，蛋白質復合物是指在相同時間和空間通過相互作用組成一個多分子機制的蛋白質集合[1]。大量的生物實驗和計算方法實驗產生了許多高質量、大規模的PPI 網絡數據，這些數據為識別蛋白質復合物奠定了基礎，而蛋白質復合物的識別能夠幫助人類預測未知的蛋白質功能，解釋特定的生物進程，并為研究疾病的發生機理，尋找新的藥物靶標，提供重要的理論基礎[2]。因此，識別蛋白質復合物是生物信息領域中的一項研究熱點。

迄今為止，早期識別蛋白質復合物的方法是生物實驗方法。雖然生物實驗方法挖掘復合物的精度較高，但是該方法不僅費時費力，檢測效率也已經不能滿足后基因組時代的發展。隨著高通量生物蛋白信息學的發展，產生了許多高質量和大規模的蛋白質相互作用數據，這些數據為采用計算方法識別蛋白質復合物奠定了基礎[3]。因此，出現了大量基于計算方法識別復合物的算法。由于生物網絡中每個蛋白質有著不同的功能，不同的邊的重要性也不同，為了更真實、詳盡地表達出蛋白質網絡結構的復雜性和多樣性，目前從加權PPI網絡中識別蛋白質復合物越來越受到人們的關注[4]。Dimitrakopoulos等人[5]提出一種從加權蛋白質網絡之中預測重疊蛋白質復合物的算法GENA（Gradually expanding dense neighborhoods）。基于COACH（Core-attachment method）方法，Kouhsar 等人[6]提出一種快速高性能的預測加權蛋白質復合體檢測算法WCOACH。Ama 等人[7]提出一種跨模塊中心移除的加權蛋白質復合物識別算法IMHRC（Inter module hub removal clustering）。雖然這些加權網絡蛋白質復合物檢測算法具有一定的成效，但是由于相互作用數據中存在著較高比例的假陽性和假陰性，以及蛋白質相互作用數據中包含不穩定或發生在不同時間點的相互作用，導致識別蛋白質復合物的精確度不高[8]。為了進一步提高識別的準確性，研究者們開始結合蛋白質相互作用以及多元生物數據來識別復合物。例如，在蛋白質相互作用網絡中，胡偉等人[9]提出蛋白質復合物識別ICMDS算法（Predicting complexes based on multiple biological data sources）。該算法整合了基因表達譜、關鍵蛋白信息和蛋白質相互作用數據。基于蛋白質相互作用數據以及異構生物數據，趙碧海等人[10]提出一種基于多關系網絡中關鍵模塊挖掘的蛋白質功能預測算法PEFM（Prediction of protein functions based on essential functional modules mining）。多元生物數據整合能夠有效地彌補相互作用網絡不完整性和噪聲的問題，使得識別蛋白質復合物的精確度得到提高。除此之外，由于模塊度函數充分考慮PPI網絡的節點分布情況，可以通過優化該函數將連接緊密的節點聚到相同的模塊中，符合蛋白質復合物的結構特征，因此研究者提出了許多基于模塊度函數的蛋白質復合物挖掘算法[11]。Becker 等人[12]提出基于層次聚類的OCG（Overlapping cluster generator）算法，該算法根據Newman 的模塊度函數將初始的重疊類迭代地融合到層次結構中，進而實現蛋白質聚類過程，然而該算法對復合物的模塊規模較敏感，難以識別規模較小的復合物。郭茂祖等人[13]首先將識別稠密子圖作為初始模塊，然后根據模塊度函數來合并初始模塊，提出了復合物識別算法BMM（Based on protein complexes modularity function for merging modules）。Shen 等人[14]在引入外部緊密關聯度和內部模塊緊密關聯度的基礎上，設計了一種基于自適應密度模塊化的蛋白質功能模塊檢測算法ADM（Adaptive density modularity）。在這個算法中，蛋白質可以自適應地選擇留在當前的模塊還是轉移到另一個模塊中。Shen 等人[15]設計了一種基于最佳鄰節點和全局量化的復合物檢測算法BN-LGQ（Best neighbour and local-global quantification）。該算法通過搜索當前簇的最佳鄰節點和計算模塊函數增量，進而確定是否將最佳鄰節點加入簇中來擴展復合物。雖然基于模塊度函數的蛋白質復合物挖掘算法已有了很大的進步，但是這些算法僅僅考慮了網絡的拓撲特性，未考慮到PPI網絡中富含的生物信息；且難以識別出重疊和規模較小的蛋白質復合物，算法的識別精度較低。雖然基于加權PPI網絡的復合物識別取得了一定的成效，但是如何有效地構建加權PPI網絡，如何降低復合物識別效果受假陽性和噪聲數據的影響；如何解決基于模塊度函數的蛋白復合物挖掘算法僅僅只考慮網絡的拓撲特性而未考慮生物信息，以及難以識別出重疊和規模較小的復合物等導致的準確率、召回率不高以及執行效率低等缺陷，仍是亟待解決的問題。

針對以上問題，本文提出了一種基于模塊度函數的加權蛋白質復合物識別算法IWPC-MF（Algorithm for identifying weighted protein complexes based on modularity function）。主要工作為：（1）融合點聚集系數改進邊聚集系數，將改進后的邊點聚集系數與基因共表達的皮爾遜相關系數相結合來構建加權蛋白質網絡；（2）基于節點權重選取種子節點，遍歷種子的鄰居節點，設計節點間的相似度度量和蛋白質附著度來獲取初始聚類模塊；（3）設計基于緊密度的蛋白質復合物模塊度函數來合并初始模塊，并最終完成復合物的識別。實驗結果表明本文算法運行效率高，聚類結果的準確率以及召回率較高。

2 相關定義

定義1（加權蛋白質網絡）[16]設G=( )V,E,P 代表加權PPI 網絡，V=( v1,v2,…,vn)代表蛋白質節點E=(e1,)代表蛋白質之間的相互作用，P=(p( e1),p( e2),…,是每條邊存在的概率權重。

定義2（邊聚集系數）[17]設無向圖G=(V ,E,P )，其中表示節點u 和v 所共有的鄰居節點數，Nu和Nv分別代表節點u 和v 的包括自身的鄰居節點集合。則對于無向圖中(u,v)的邊聚集系數（Edge Clustering Coefficient，ECC）定義為：

定義3（皮爾遜相關系數）[18]給定k 個不同時刻的基因表達數據樣本，則兩個蛋白質節點u 和v 之間的皮爾遜相關系數（Pearson Correlation Coefficient，PCC）計算方式如式（2）所示：

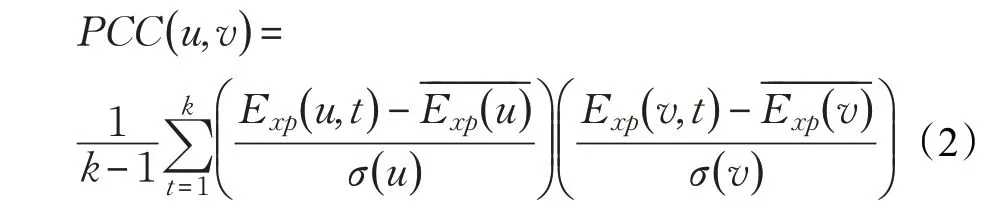
定義4（模塊度函數）[19]給定PPI 網絡G=(V ,E )，其中Aij表示節點i 和j 鄰接關系，θ( ci,cj)表示節點i和j 的模塊關系，di和dj分別代表節點i 和j 節點的度。則模塊度函數（Modularity Function，MF）的定義如式（3）所示：

3 IWPC-MF算法

3.1 算法思想

針對蛋白質相互作用網絡存在不穩定性，復合物的識別效果容易受到假陽性和噪聲數據的影響；基于模塊度函數的蛋白復合物挖掘算法只考慮網絡的拓撲特性而未考慮生物信息以及難以識別出重疊和規模較小的復合物等問題，為提高算法的準確率、召回率、執行效率和降低假陽性的影響，本文提出了一種加權蛋白質復合物識別算法IWPC-MF。具體IWPC-MF算法思想為：首先以蛋白質相互作用網絡為框架，融合點聚集系數改進邊聚集系數得到邊點聚集系數，利用邊點聚集系數與基因共表達的皮爾遜相關系數衡量相互作用邊的可靠性進而構建加權網絡；其次利用節點權重選取種子節點，遍歷種子節點的鄰域節點，利用本文設計的節點間的相似度度量和蛋白質附著度來獲取初始聚類模塊；最后基于節點緊密度改進模塊度函數，進而利用模塊度函數將有重疊的初始模塊進行合并，并最終完成復合物識別。

3.2 加權網絡的構建

針對蛋白質相互作用網絡存在不穩定性，復合物的識別效果容易受到假陽性假陰性和噪聲數據的影響，本文基于PPI網絡的拓撲特性，結合基因共表達的皮爾遜相關系數，對蛋白質相互作用網絡進行加權，并且添加新的相互作用，能一定程度上增加蛋白質相互作用的可信度。

3.2.1 PPI網絡的拓撲特性

由于蛋白質相互作用網絡具有小世界特性和稀疏性，且存在一定比例的假陽性和假陰性，若兩個蛋白質都同時第三個蛋白質發生相互作用，則這兩個蛋白質間相互作用假陽性的可能性比較小，共同參與模塊執行相同功能的概率比較大，因此，一對蛋白質之間相互作用的概率可以通過它們共有的鄰居節點數量確定[20]。基于節點間共有的鄰居數量的邊聚集系數是PPI 網絡中重要的拓撲特性，可以用于衡量測度圖中的邊聚集在一起的程度，還可以評估節點鄰居之間的緊密程度。但是邊聚集系數僅僅考慮邊的重要性，沒有考慮節點的重要性。因此，引入能夠反映節點聚集程度的點聚集系數[21]對邊聚集系數加以改進，提出一種融合節點和邊的雙重拓撲特性的邊點聚集系數，則邊點聚集系數度量如式（4）所示：

式（4）中，| Nu∩Nv|表示集合Nu除去和集合Nv的交集部分所剩余的蛋白質個數，| Nv-Nu|表示集合Nv除去和集合Nu的交集部分所剩余的蛋白質個數，Cu和Cv分別表示節點u 和v 的點聚集系數，其度量方式如式（5）所示：

式（5）中，i 可分別代表節點u 和v，| |Ni代表節點u 或v 的度，| |Ei表示由節點u 或v 的鄰居節點之間組成的邊的數目。

3.2.2 蛋白質的皮爾遜相關系數

由于高通量實驗獲得的蛋白質相互作用數據中存在著一定比例的假陽性和噪聲數據，如果僅僅用網絡的拓撲特性來衡量兩個蛋白質之間的相互作用程度是比較片面的，因此本文引入定義3的基因共表達皮爾遜相關系數來衡量兩個蛋白質之間的共表達程度進而增強相互作用之間的可靠性。

3.2.3 蛋白質網絡的加權

基于蛋白質相互作用網絡的拓撲特性，整合皮爾遜相關系數對網絡進行加權，該加權策略不僅考慮了邊和點聚集的重要性，還考慮到相互作用的蛋白質之間的基因共表達程度，共同體現蛋白質相互作用的可信度，其邊加權的權重越大，可信度就越高。則對于PPI網絡中任意兩個蛋白質之間的相互作用(u,v)的權重計算如式（6）所示：

本文根據網絡的拓撲特性和生物基因共表達皮爾遜相關系數構建加權網絡，將邊權值為0的邊刪除來降低噪聲數據對挖掘蛋白質復合物檢測結果造成的負面影響。

權值為0的邊刪除的必要性分析如下：

大量研究表明，通過高通量的生物實驗方法獲得的蛋白質相互作用數據中包含著較高比例的假陽性和假陰性，為了減少假陽性和假陰性造成的負面影響，本文通過綜合考慮蛋白質網絡的拓撲特性即蛋白質相互作用邊之間的緊密聯系以及節點的聚集系數來降低假陽性的影響，以及生物數據即皮爾遜相關數據來添加新的蛋白質相互作用，進而減少假陰性的影響。綜合分析蛋白質相互作用的拓撲特性和生物特性來構建加權蛋白質網絡，故將邊權值為0的邊作為假陽性而進行刪除。

降低噪聲數據對挖掘蛋白質復合物檢測結果造成的負面影響等方面的作用分析：

為了進一步分析降低噪聲數據對挖掘蛋白質復合物檢測結果造成的負面影響，分別將邊權重為0的邊刪除以及不刪除邊權重為0的邊，利用本文改進的方法來挖掘蛋白質復合物，具體識別出的復合物的基本信息如表1所示。

表1 復合物的基本信息

從表1 可以看出，未刪除邊權重為0 的邊的蛋白質復合物的平均蛋白質的個數為11.6，比刪除邊權重為0的邊挖掘的復合物的平均個數要少，以及識別出的復合物比刪除邊權重為0 的復合物的個數要少。這是由于未刪除邊權重為0 的邊中存在噪聲數據實驗結果容易受到假陽性的影響。故本文方法將邊權重為0 的邊刪除可以有效地減少和控制噪聲對于蛋白質復合物檢測所產生的負面影響。

3.3 初始模塊的形成

初始模塊的形成過程主要包括節點種子的選取，根據節點間的相似性，遍歷種子節點的鄰域，計算蛋白質間的附著度進而形成初始模塊。

基于蛋白質網絡的拓撲特性和皮爾遜相關系數構建的加權網絡，節點u 所有關聯的邊點聚集系數之和即節點權重定義如式（7）所示：

基于蛋白質復合物成簇出現且高度共表達，則蛋白質間的相似度度量如式（8）所示：

式（8）中，PCC( i,j )表示節點間的皮爾遜相關系數，PECC( i,j )表示節點i 和j 之間的結構相似性，Ni代表節點i 的鄰居節點集合。PCC( i,j )和PECC( i,j )的差值表示節點共表達程度與拓撲結構相似性的差異，差異越小，說明這兩個蛋白質無論是拓撲結構還是基因共表達信息的相似度都很接近，模塊劃分結構越加穩定。其值越大，說明這兩個節點越有可能在同一模塊內。

根據蛋白質節點之間的相似度度量，綜合考慮節點與鄰域節點間以及節點與鄰域節點的鄰接節點的相似度，設計出蛋白質附著度度量公式。

給定加權蛋白質子網絡WG1=( )V1,E1,P1和節點i ∈V1，SM( )i,j 為節點間的相似性度量，加權網絡G2=(V2,E2,P2)是包含G1中所有節點的鄰居節點以及對應的相互作用邊。則節點i 的的附著度計算如式（9）所示：

初始模塊的形成思想如下：首先，基于蛋白質復合物是成簇出現且傾向于共表達的事實，利用式（6）來計算邊的存在概率，構建加權網絡；接著充分考慮節點之間的緊密程度以及共表達程度，對于加權網絡中的任意一個節點，利用式（7）來計算該節點在其鄰居圖中的節點的權重，將加權網絡中的邊權值為0 和節點權重為0的作為噪聲移除，同時按照WP( )u 值進行降序排列作為擴張的種子節點；最后遍歷種子節點的鄰域，根據相似度度量式（8）來計算節點間的相似性，同時根據式（9）計算蛋白質節點的附著度，將附著度大于閾值的節點加入到種子節點中，重復進行操作形成初始模塊。

初始模塊的形成過程形式化如下：

輸入：蛋白質網絡G( )

V,E ，附著度閾值δ，基因表達數據

輸出：初始模塊集合EM（1）構建加權蛋白質網絡

①For each ( u,v )∈E do

② Compute PECC( u,v )by Eq（.4）

③ Compute PCC( u,v )by Eq（.2）④ Compute P( u,v )by Eq（.6）

⑤ If P( u,v )=0 do

⑥ Remove（）//除去權值為0的相互作用邊

⑦ End if

⑧End for

（2）選取種子節點

①L=? //種子節點集合

②For each vi∈V do

③ Compute WP( vi)by Eq（.7）

④ Sort（）//將蛋白質節點按照WP( vi)值非遞減排序WP( v1)≥WP( v2)≥…≥WP( vk)進入種子節點集合L 中。

⑤End for

（3）初始模塊形成

①EM=?，L={v1,v2,…,vk}

②For each vi∈L do

③G1={vi|dis( vi,va=1) }∪{vi}

④ If DS( vi,G1)＞δ do

⑤ EM=EM ∪{vi}

⑥ End if

⑦End for

⑧ Return EM //輸出蛋白質初始模塊

3.4 初始模塊的合并

大量研究發現，不同的蛋白質復合物之間可能存在重疊；大多數蛋白質復合物所包含的蛋白質節點數目較少；而且蛋白質復合物往往是傾向于成簇和高度共表達出現[13]。然而基于模塊度函數的蛋白復合物挖掘算法存在僅僅只考慮網絡的拓撲特性而未考慮生物信息以及難以識別出重疊和規模較小的復合物等問題，為提高算法的準確率和召回率，基于蛋白質網絡的拓撲特性和基因共表達皮爾遜相關系數構建的加權網絡，考慮到蛋白質復合物是節點緊密連接的稠密子圖和蛋白質網絡本身具有的小世界特性，提出基于緊密度[22]的蛋白質復合物合并模塊度函數，若相鄰的模塊能夠使模塊度函數增加，則對模塊進行合并進而得到蛋白質復合物。

緊密度是保證形成高內聚復合物的形成條件之一，則一個蛋白質節點v 到模塊S 的緊密度F(v)的計算方式如式（10）所示：

基于緊密度的模塊度函數計算公式如式（11）所示：

式（11）中，網絡中邊的數目為 ||E ，當前網絡的模塊數為| EM |，Si和Sj分別表示節點i 和j 所在的模塊。

為了能夠識別出更多規模較小和重疊的蛋白質復合物進而提高識別的精度，基于改進后的模塊度函數，若初始兩個模塊合并能使模塊度函數值增加，則合并這兩個模塊，并更新模塊度函數值。

基于緊密度的模塊度函數，具體模塊合并過程形式化如下：

輸入：加權蛋白質網絡WG(V,E)，初始模塊集合EM

輸出：蛋白質復合物集合C

（1）C=?

（2）For i =1 to| EM |-1

（3）Compute DMF( EM′ )//計 算EMi和EMi+1合并后的EM′的模塊度函數值

（4） If FMF( EM′ )＞FMF( EM )do

（5） EMi=EMi∪EMi+1//刪除EMi+1

（6） FMF( EM )=FMF( EM′)

（7） C=EM

（8） End if

（9）End for

（10）Return C //輸出蛋白質復合物

3.5 IWPC-MF算法步驟

IWPC-MF算法具體的實現步驟如下所示：

輸入：蛋白質網絡G(V,E，基因表達數據

輸出：蛋白質復合物C

（1）初始化參數：附著度閾值δ

（2）蛋白質復合物的挖掘

①For each ( u,v )∈E do

② 調用加權網絡形成過程，獲得加權網絡WG(V,E)

③ For each vi∈V do

④ 調用種子節點形成過程，獲得種子節點集合L

⑤ For each vi∈L do

⑥ 調用初始模塊形成過程，獲得初始模塊集合EM

⑦For i=1 to| EM |-1

⑧調用初始模塊合并過程，獲得蛋白質復合物集合C

⑨End for

⑩ End for

? End for

?End for

?Return C //得到蛋白質復合物

3.6 算法的時間復雜度

IWPC-MF 算法的計算復雜度由以下幾個步驟構成：假設PPI 網絡中節點數目為n，依據邊點聚集系數以及基因表達數據構建加權PPI 網路的時間復雜度為O(n2)；基于節點權重來選取種子節點的時間復雜度為O(n2)；遍歷種子節點的鄰域，通過計算蛋白質節點之間的相似性，采用蛋白質附著度來形成初始模塊的時間復雜度為O(n2)；假設初始的模塊數為h，則模塊合并的時間復雜度為O(h2)。因此，IWPC-MF算法的時間復雜度為O(n2+h2)。由于h ＜n，所以IWPC-MF 算法的時間復雜度近似為O(n2)。而在GENA 算法中，算法的時間復雜度主要取決于初始化以及優化集群的過程，即O(Bn3)；在WCOACH 算法中，算法的時間復雜度主要取決于初始核的檢測和添加附件形成蛋白質復合物的過程，即O(τn3)；在IMHRC 算法中，算法的時間復雜度主要取決于主要蛋白質集群形成以及合并修復集群的過程，即O(pγβn2)；在ICMDS 算法中，算法的時間復雜度主要取決于復合核的形成以及冗余過濾，即O(n3)；在OCG 算法中，算法的時間復雜度主要取決于極大團的形成以及合并模塊的過程，即O(hn2)；在BMM算法中，算法的時間復雜度主要取決于初始模塊的形成以及合并模塊的過程，即O(n2+h2)，雖然該算法的復雜度和本文算法的時間復雜度一樣，但該算法的識別精度以及匹配率較低；在ADM算法中，算法的時間復雜度主要取決于外部和內部緊密關聯度的計算以及合并模塊的過程，即O(n3)；在BN-LGQ算法中，算法的時間復雜度主要取決于模塊化增量計算以及模塊形成過程，即O(n+φn+)。上述提及的nc、T 、τ、γ、β、B、φ 和χ 分別表示最大的復合物的蛋白質數目、基因表達時刻數、鄰域親和力閾值、中心獲取閾值、中心移除閾值、預測到的模塊數目、復合物形成前的數量和合并過程中蛋白質復合物減少的數量。

4 實驗結果以及分析

4.1 實驗環境

IWPC-MF 算法實驗的編程環境為Python3.5.2；操作系統為Windows10 家庭中文版；內存12 GB；處理器為Intel?CoreTMi5-4200H CPU @ 2.8 GHz。

4.2 實驗數據集

為驗證本文提出算法的有效性，選用蛋白質相互作用數據相對完整和可靠的酵母蛋白質相互作用網絡數據作為實驗數據。具體實驗數據如下所示：

（1）酵母PPI網絡數據來源于DIP數據庫[23]，去除重復以及自相互作用，該數據庫包含4 995個蛋白質和21 554對相互作用。

（2）實驗采用的時序基因表達數據為GSE3431[24]，包含7 079個蛋白質和36個時刻下的基因表達值。

（3）本文采用CYC2008[25]作為標準數據集，該數據集包含408個通過生物實驗預測得到的蛋白質復合物。

4.3 評價指標

4.3.1 精度、召回率和F-measure 度量

為了評價本文算法的有效性，采用文獻[26]的基于鄰域親和評分的精度(Precision)、召回率(Recall)和F度量(F-measure)指標來評價算法性能。鄰域親和評分是用來衡量預測的復合物與實際復合物的匹配度即重疊率，當重疊率OS(p,b)≥ω，輸出最終的復合物，否則將該復合物刪除，其定義為：

綜合考慮精度和召回率對聚類結果的影響，采用F-measure 綜合評估整體算法的性能。其計算公式如下：

4.3.2P-value值度量

隨著蛋白質組學研究的深入，使得一個蛋白質與其功能注釋相對應成為可能，蛋白質簇發生對于一個給定功能注釋在統計學上的意義就可以通過一個超幾何分布的等式來進行計算[28]：

其中，V 代表PPI 網絡中包含的蛋白質總數，C 為預測挖掘出的復合物數目，F 為一個功能組數量，k 為C 中包含F 中的蛋白質數目。

4.4 參數選擇

IWPC-MF 算法中，由于參數δ 的取值影響實驗的聚類效果，因此本文在不同的δ 參數取值上獨立運行20次實驗，取20次實驗的平均值進行分析。在圖1中展示了δ 在不同取值下的F-measure 值和被識別匹配的蛋白質復合物比例變化情況，具體的實驗結果如圖1所示。

圖1 F-measure 值和匹配的蛋白質復合物比例變化圖

圖1 可知，隨著δ 從0 到0.2 逐漸增大，F-measure的值在δ 不同取值之下也逐漸增大，且F-measure 達到最大值0.482 9，實驗識別的復合物和已知的復合物的匹配比例也逐漸增加，且達到最大值65.51%；隨著δ 從0.2到1逐漸增大，F-measure 的值在δ 不同取值之下逐漸降低，實驗識別出的復合物和已知的復合物的匹配比例也逐漸降低。這是因為本文融合邊點聚集系數與基因表達數據構建加權網絡，同時利用節點權重來選取種子節點，遍歷種子節點的鄰居時，計算節點之間的相似度，根據蛋白質附著度來形成初始模塊，充分考慮了內部節點與外部節點之間的聯系即全局一致性。隨著附著度閾值的增大，算法識別的聚類數目逐漸增加，每個復合物中包含的蛋白質數目越少，相對應復合物的個數就會增加，但是當閾值增大到一定值時，擴展的種子鄰域節點和種子節點之間的相互作用要求提高，導致挖掘復合物的精度逐漸增加，對挖掘出的蛋白質復合物會更嚴格，導致算法F-measure 值和匹配比例先增加后降低。通過觀察發現存在一對合理取值即δ=0.2，使F-measure達到最大值0.482 9且匹配比例達到65.51%。故本文設置δ=0.2。

4.5 邊點聚集系數度量的有效性分析

為了驗證IWPC-MF 算法使用邊點聚集系數PECC度量公式的有效性，分別基于使用邊點聚集系數度量和皮爾遜相關系數IWPC-MF-PECC-PCC加權的IWPC-MF算法和未使用邊點聚集系數即使用邊聚集系數ECC和皮爾遜相關系數IWPC-MF-ECC-PCC加權的IWPC-MF算法，比較在算法識別的復合物與已知的復合物的匹配重疊率不同閾值下得到的F-measure 值和匹配比例，具體的實驗結果如圖2所示。

圖2 不同加權策略挖掘的復合物對比結果

由圖2 顯示，使用邊點聚集系數度量的IWPC-MF算法的F-measure 取值和匹配的蛋白質復合物比例都比未使用邊點聚集系數的取值要高。在本文取值重疊率閾值為0.2 時，F-measure 的取值比未使用邊點聚集系數提高3.62%，匹配的蛋白質復合物比未使用邊點聚集系數度量加權提高4.65%。實驗結果說明，使用改進的邊點聚集系數的算法的聚類效果得到了提高。這是因為：基于復合物內部節點之間的緊密聯系，IWPC-M算法在充分考慮網絡的拓撲特性以及基因共表達程度時，還考慮到節點的聚集程度對復合物挖掘的影響，利用邊點聚集系數和皮爾遜相關系數對蛋白質網絡進行加權，進而利用種子節點實現復合物的挖掘。也進一步證明利用種子蛋白質能很好擴展為一個復合物。

為進一步檢驗邊點聚集系數的有效性，分別使用不同加權方法與本文的IWPC-MF-PECC-PCC加權方法進行對比實驗，圖3是采用不同加權方法檢測到蛋白質復合物與標準數據庫的對比結果。從圖3可以看出，使用IWPC-MF-ECC 加權的方法未識別出YHR081W 和YOL142W 兩個蛋白質，是因為邊聚集系數只考慮節點間邊的緊密度，對網絡的拓撲性分析比較單一；使用IWPC-MF-PECC 加權的方法未識別出一個蛋白質，這是因為邊點聚集系數不僅考慮了節點間邊的緊密關系，還考慮到了每個節點的重要性，對蛋白質網絡的拓撲特性考慮得較全面，但忽略了蛋白質之間的生物特性；使用IWPC-MF-PECC-PCC加權的方法既考慮到網絡的拓撲特性，同時又結合基因共表達的皮爾遜相關系數，對蛋白質網絡的分析比較全面，能夠更加貼近真實網絡，因此最終的聚類效果較好。

4.6 加權蛋白質網絡的性能分析

為了進一步分析IWPC-MF算法結合邊點聚集系數和皮爾遜相關系數構建加權網絡的性能，分別基于邊點聚集系數和皮爾遜相關系數IWPC-MF-PECC-PCC加權的蛋白質網絡、邊點聚集系數IWPC-MF-PECC 構建的加權網絡和皮爾遜相關系數IWPC-MF-PCC 構建的加權網絡來挖掘蛋白質復合物，比較算法識別的復合物與已知的復合物在不同匹配重疊率閾值之下的匹配比例，具體的實驗結果如圖4所示。

由圖4顯示，本文使用邊點聚集系數和皮爾遜相關系數IWPC-MF-PECC-PCC構建加權蛋白質網絡挖掘復合物的檢測效果明顯優于其他加權策略，尤其在匹配重疊率閾值為0.2時，IWPC-MF算法使用IWPC-MF-PECCPCC加權識別的蛋白質復合物匹配比例分別比使用PECC加權和PCC加權識別的匹配比例高3.00%和5.83%。實驗結果說明，結合邊點聚集系數和皮爾遜相關系數的算法的聚類效果得到了提高。這是因為：基于邊點聚集系數加權的蛋白質網絡僅僅整合了邊聚集系數和點聚集系數，因此只能反映PPI 網絡的拓撲特性，考慮得比較單一；基于皮爾遜相關系數加權的網絡僅僅只考慮到基因共表達程度，沒有考慮網絡的拓撲特性，實驗結果存在較高的假陽性和假陰性數據；而基于復合物內部節點之間的緊密聯系，IWPC-MF 算法在充分考慮網絡的拓撲特性以及基因共表達程度時，還考慮到節點的聚集程度對復合物挖掘的影響，結合邊點聚集系數和皮爾遜相關系數對蛋白質網絡進行加權，有效地減少假陰性和假陽性帶來的負面影響，因此本文的加權蛋白質網絡的性能較好。

圖3 不同加權方法識別nuclear exosome complex復合物

圖4 不同加權網絡策略的蛋白質匹配比例值的對比分析

為了減少假陽性和假陰性造成的負面影響，本文通過綜合考慮蛋白質網絡的拓撲特性即蛋白質相互作用邊之間的緊密聯系以及節點的聚集系數來降低假陽性的影響，以及生物數據即皮爾遜相關數據來添加新的蛋白質相互作用，進而減少假陰性的影響。綜合分析蛋白質相互作用的拓撲特性和生物特性來構建加權蛋白質網絡。為了進一步分析本文方法PPI 網絡任意兩個蛋白質之間的相互作用權重計算方式設計的準確性，采用本文的加權方式以及采用邊點聚集系數構建加權網絡來挖掘蛋白質復合物，具體檢測結果如圖5所示。通過具體實例分析DNA-directed RNA polymerase II complex復合物中任意邊的相互作用，發現本文加權識別的復合物更加貼近真實網絡。本文設計的加權方法更加準確。

4.7 優化的模塊度函數的有效性分析

為了驗證IWPC-MF算法使用優化的模塊度函數FMF的有效性，分別基于優化的模塊度函數FMF 的IWPCMF算法和未使用該優化函數即使用MF函數的IWPCMF算法，在DIP數據庫獨立執行20次進行復合物的識別，實驗檢測結果對比分析如圖6所示。

圖6 顯示的是使用優化的模塊度函數FMF 的IWPC-MF算法在precision、recall、F-measure 取值和匹配的蛋白質復合物比例與未使用該優化函數即使用MF函數的對比情況，其中使用FMF的precision 的取值比使用MF函數提高6.73%，recall 的取值比使用MF函數提高7.80%，F-measure 的取值比使用MF 函數提高7.40%，匹配的蛋白質復合物比使用MF函數提高6.73%。這是因為，本文根據使用FMF 函數來對初始模塊進行合并，充分考慮網絡的拓撲特性以及基因表達程度的同時，也考慮到復合物的重疊性以及復合物規模較小的性質，使得挖掘的復合物較準確，避免存在較高比例的復合物之間功能相似的模塊，實驗結果說明，使用FMF函數的算法的聚類效果較優。

圖5 蛋白質邊權重的準確性對比分析

在PPI 網絡中，通過對蛋白質復合物的結構分析，可以發現多數蛋白質復合物的規模較小[13]；而且同一個蛋白質可能屬于不同功能的復合物，這些蛋白質往往具有多個生物功能，即蛋白質復合物之間可能會存在重疊。

圖6 優化的模塊度函數的對比分析

在標準408個復合物中，根據文獻[13]的記錄，標準復合物實際體積大于20 的只有不到10 個，半數以上的蛋白質復合物體積不大于3。為了驗證本文識別蛋白質復合物的改進方法對規模較小復合物的識別能力，采用復合物體積來表示復合物中包含的蛋白質的個數，具體的蛋白質復合物體積分布直方圖如圖7所示。

圖7 蛋白質復合物體積分布直方圖

從圖7可以看出，利用本文改進的方法檢測到的體積大于21的不到9個，但是半數以上的復合物的體積不大于6。這說明多數蛋白質復合物的規模較小，且本文改進的方法可以識別出規模較小的復合物。

圖8 蛋白質復合物體積分布直方圖

從圖8可以看出蛋白質復合物的重疊分布情況，其中重疊的蛋白質個數為2個和3個的蛋白質復合物數目最多，分別達到了124個和121，分別占本文識別的374個復合物的33.16%和32.35%。從圖7和圖8可知，本文改進的方法對規模較小和重疊蛋白質復合物的識別能力較優。這是因為本文綜合考慮網絡的拓撲特新和生物特性，以及使用基于緊密度的改進的模塊度函數來合并初始模塊，能夠識別出重疊和規模較小的復合物。

4.8 算法性能的比較分析

本節將IWPC-MF 算法分別從精度、召回率和F-measure 的比較分析、聚類效果的比較分析和功能富集的比較分析與GENA[5]、WCOACH[6]、IMHRC[7]、ICMDS[9]、OCG[12]、BMM[13]、ADM[14]、BN-LGQ[15]算法進行比較分析。重復迭代次數20次。實驗使用到的參數設置δ=0.2。

（1）精度、召回率和F-measure 的比較分析

為了驗證本文算法的性能，將IWPC-MF 算法與其他8種算法在DIP數據上獨立運行20次，取實驗結果的平均值進行分析，得到各個算法識別的復合物基本信息以及實驗評價指標對比分析如表2和圖9所示。

表2 各算法識別的復合物的基本信息

圖9 算法性能比較關系圖

在表2 中，PM 表示算法識別出的復合物總數，average 是指每個簇中的蛋白質平均個數。由表2可以知道，IWPC-MF 算法共識別374 個復合物，每個復合物平均包含13.5 個蛋白質，其中245 個預測結果較準確，標準集合中的156個復合物可以被算法準確識別到，是所有算法中識別匹配最多的。這是因為IWPC-MF算法在構建加權蛋白質網絡的時候不僅考慮了蛋白質網絡本身的拓撲特性，還考慮到蛋白質之間的基于共表達程度，這樣降低了假陽性和噪聲數據對實驗結果產生的負面影響；同時利用優化后的模塊度函數合并初始模塊時，充分考慮蛋白質復合物之間的重疊性以及大多數復合物規模較小的特性，這樣可以提高識別的準確性。因此，本文提出的IWPC-MF算法的挖掘效果較好。

圖9顯示了各種算法在DIP數據集中識別的復合物的結果。從圖中可以清晰地發現IWPC-MF 算法在精度、召回率和F 度量指標上取得較好的結果。具體來說，IWPC-MF 算法的精度為65.51%，相比較GENA、WCOACH、IMHRC、ICMDS、OCG、BMM、ADM 和BNLGQ 算法分別提高了39.69%、57.75%、14.17%、3.74%、43.93%、40.44%、44.66%和40.67%；召回率為38.24%，相比較GENA、WCOACH、IMHRC、ICMDS、OCG、BMM、ADM 和BN-LGQ 算法分別提高了79.31%、90.24%、52.94%、8.33%、65.96%、59.18%、83.53%和54.46%；F 值度量為48.29%，相比較GENA、WCOACH、IMHRC、ICMDS、OCG、BMM、ADM 和BN-LGQ 算法分別提高了64.71%、78.27%、38.65%、6.64%、57.84%、52.27%、69.21%和49.38%。實驗結果表明，使用本文算法挖掘蛋白質復合物的聚類精度、召回率和F-measure 相比較其他8種算法都得到了提高。這是因為，在GENA算法中，使用貪婪方法初始化集群，在聚類系數的基礎上選取種子節點，僅僅考慮了網絡的拓撲特性，挖掘的效果存在大量的重疊模塊；在WCOACH 算法中，僅僅利用GO 信息來構建加權網絡，缺乏考慮蛋白質網絡本身的拓撲特性以及特征，且在聚類的時候，若選取的核心節點較為相似，則會挖掘出大量重疊的模塊，最終導致挖掘的準確性降低；在IMHRC算法中，構建加權PPI網絡時，僅僅考慮節點度即網絡的拓撲結構，沒有融合生物信息，考慮構建的加權PPI 網絡比較單一，使得挖掘聚類效果不佳。在ICMDS 算法中，基于邊聚集系數和皮爾遜相關系數，在計算相互作用的功能相似性時引入了自定義的參數，導致挖掘效果受參數的影響比較大；在OCG、BMM、ADM和BN-LGQ算法中，僅僅只考慮網絡的拓撲特性而未考慮生物信息以及難以識別出重疊和規模較小的復合物。而本文是綜合考慮網絡的拓撲結構和生物基因表達信息，基于邊點聚集系數和皮爾遜相關系數來構建加權網絡；同時根據節點權重選擇種子節點，遍歷種子節點的鄰域，利用蛋白附著度來形成初始模塊；最后利用改進的模塊度函數合并有重疊的模塊，可以較為精確和快速地挖掘出蛋白質復合物。因此，本文提出的算法的聚類效果較好。

（2）聚類效果的比較分析

為了評估本文提出的IWPC-MF 算法的聚類效果，將本文算法與其他8種算法挖掘的Elongator holoenzyme復合物可視化，對比分析聚類效果，聚類聚類結果的對比如圖10所示。

圖10 各個算法的復合物挖掘可視化比較圖

圖10 顯示了不同算法檢測到的Elongator holoenzyme復合物結果，圖（a）是該標準復合物所包含的蛋白質相互作用情況；圖（b）是本文算法的檢測結果；圖（c）是GENA 算法的檢測結果；圖（d）是算法WCOACH 的檢測結果；圖（e）是IMHRC算法的檢測結果；圖（f）是算法ICMDS的檢測結果；圖（g）是OCG算法的檢測結果；圖（h）是BMM算法的檢測結果；圖（i）是ADM算法的檢測結果；圖（j）是BN-LGQ 算法的檢測結果。通過圖10顯示，本文算法能夠準確地識別蛋白質復合物；GENA算法識別出標準復合物中的6個蛋白質，但是也包含了2 個非Elongator holoenzyme 復合物內的蛋白質；算法WCOACH 識別出標準復合物中的5 個蛋白質；算法IMHRC識別出標準復合物中的6個蛋白質，但是也包含了3 個非Elongator holoenzyme 復合物內的蛋白質；ICMDS算法也正確識別出標準復合物中的6個蛋白質；OCG 算法識別出標準復合物，但是也包含了4 個非Elongator holoenzyme復合物內的蛋白質；BMM算法識別出標準復合物中的6 個蛋白質，但是也包含了5 個非Elongator holoenzyme復合物內的蛋白質；ADM算法識別出標準復合物中的6 個蛋白質，但是包含了4 個非Elongator holoenzyme 復合物內的蛋白質；BN-LGQ 算法識別出標準復合物中的6 個蛋白質，但是也包含了1個非Elongator holoenzyme復合物內的蛋白質。實驗結果表明，本文算法挖掘的蛋白質復合物聚類效果較好。這是因為，本文通過蛋白質網絡的拓撲特性和基因表達信息來構建加權網絡，可以降低假陽性和噪聲數據的負面影響；同時根據節點權重選擇種子節點，遍歷種子節點的鄰域，利用蛋白質附著度來形成初始模塊，綜合考慮蛋白質復合物是稠密且內部緊密連接的特性，以及蛋白質復合物成簇出現和高度共表達的特性；將得到的初始模塊利用改進的模塊度函數進行合并，充分考慮到蛋白質復合物的重疊性以及規模較小的特性，同時也避免算法重復的挖掘過程。實驗結果表明，本文算法在識別蛋白質復合物上具有較好的聚類效果。

（3）功能富集的比較分析

為了測試算法識別的復合物的生物學意義，采用復合物的低P-value 值的功能富集分析。 P-value 值越小表明該復合物具有很高的統計學意義。若一個模塊的P-value ＜0.01，則認為這個復合物是顯著的[29]。顯著的復合物數量在識別出的復合物總數中所占的比例可以很好地評價各個算法的整體性。具體各個算法性能比較如表3所示。

表4 IWPC-MF算法識別的復合物實例

表3 各個算法識別的復合物的顯著性統計信息

在表3中，PM 表示算法識別出的復合物總數，SC表示具有生物顯著意義的蛋白質復合物數目。IWPCMF算法識別的復合物數目中顯著性復合物的比例達到85.29%，相比較GENA、WCOACH、IMHRC、ICMDS、OCG、BMM、AD 和BN-LGQ 算法分別提高了83.22%、14.81%、73.42%、3.19%、82.24%、70.58%、77.28%和53.62%。由此可見，IWPC-MF 算法識別出的復合物具有很強的生物統計學意義。這是因為本文算法在構建加權網絡的時候，綜合考慮網絡的拓撲特性和基因共表達程度，同時根據蛋白質附著度利用種子節點形成初始模塊，最后綜合考慮復合物的重疊性和規模較小的性質，利用基于緊密度的模塊度函數實現復合物的挖掘。最終導致聚類效果較好，執行效率高，挖掘的生物蛋白質復合物更具有生物統計意義。

表4具體給出本文IWPC-MF算法識別出的復合物實例，其中OA 表示算法識別復合物的匹配率，OM 表示的是正確匹配的蛋白質個數，Predicted protein 表示組成復合物的所有蛋白質，加粗部分表示被匹配的蛋白質。從表4 可以看出，當P-value=2.22E-18 時，本文算法識別的NatC 復合物的匹配率達到了0.82，正確匹配的蛋白質個數是9，這是因為YGR134W和YNL288W蛋白質與復合物內部連接比較松散。由此可見，IWPCMF算法識別的蛋白質復合物效果更好。

5 結束語

本文在結合邊點聚集系數與基因表達數據構建的加權蛋白質網絡基礎上，提出一種基于模塊度函數的加權蛋白質復合物識別算法IWPC-MF。基于節點權重選取種子節點，遍歷種子的鄰居節點，設計節點間的相似度度量和蛋白質附著度來獲取初始聚類模塊；設計基于緊密度的蛋白質復合物模塊度函數來合并初始模塊，并最終完成復合物的識別。為了評估算法的性能，本文將IWPC-MF算法與其他8種算法進行了對比，實驗結果表明，IWPC-MF 算法具有更高的準確率、召回率，識別的復合物具有更強的生物統計意義。今后可以將IWPC-MF算法應用于疾病預測和關鍵蛋白質識別等相關研究中。