預測低合金鋼試樣破壞的彈塑性斷裂模型

管俊峰，宋志鍇，白衛峰，姚賢華，陳珊珊，謝超鵬

(華北水利水電大學土木與交通學院，河南，鄭州450045)

金屬材料的斷裂韌度與強度(屈服強度與極限強度等)是其重要的材料性能參數。若采用線彈性斷裂理論確定金屬材料無尺寸效應的斷裂韌度，所用試樣尺寸以及預制裂縫長度就須大于一定值，才能忽略裂縫尖端塑性區的影響。目前，基于線彈性斷裂理論確定金屬斷裂韌度的試樣尺寸及試驗條件的研究已較充分，相關成果已應用于國內外規范，如：金屬材料平面應變斷裂韌度KIC試驗方法(GB/T 4161-2007)[1]、金屬材料準靜態斷裂韌度的統一試驗方法(GB/T 21143-2007)[2]、金屬材料表面裂紋拉伸試樣斷裂韌度試驗方法 (GB/T 7732-2008)[3]、美國ASTM E399規范[4-5]、歐洲BS EN ISO規范[6]，等。上述規范中斷裂韌度的測試試樣尺寸須滿足：

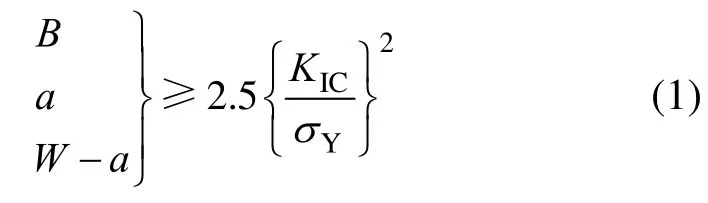
式中：B為試樣厚度；a為試樣預制裂縫長度；W為試樣尺寸；W-a為試樣韌帶高度；KIC為平面應變情況下金屬材料的斷裂韌度；σY為金屬材料的屈服強度。上述規范中要求，測試前須對所用金屬試樣進行疲勞試驗形成初始裂縫a。另外，試驗過程中，對試樣型式、加載夾具、加載方式、試驗系統等都有嚴格限制。因此，在普通實驗室，金屬斷裂韌度的測試較難完成。

若金屬試樣的尺寸小于規范規定的最小尺寸(式(1))，則試樣裂縫尖端的塑性區大小，與預制裂縫及試樣尺寸相比不能忽略，試樣破壞處于彈塑性斷裂控制；由其試驗結果直接采用線彈性斷裂理論來確定的材料參數，存在尺寸效應。為克服小尺寸金屬試樣的確定結果的尺寸效應問題，20世紀50年代末和60年初，Barenblatt[7]和Dugdale[8]等開始研究并發展建立彈塑性斷裂力學理論，之后學者們不斷完善其理論并擴展其應用范圍[9-16]：如Rice[9]建立了J積分理論；Cotterell等[10]提出斷裂功的概念；Mai等[11]采用J積分研究確定韌性材料的斷裂功；Hu和Guan等[12-24]建立了考慮試樣尺寸與初始裂縫的相互影響的邊界效應斷裂理論；等等。進一步，學者們基于彈塑性理論與模型的發展，開展了相應的應用研究。然而到目前，其應用研究仍停留在測試金屬R曲線及裂縫嘴張開口位移CTOD等彈塑性斷裂指標等方面[25-28]，如美國ASTM規范明確規定了確定金屬JR曲線的標準方法[29]。而實際工程中，較多情況下的金屬結構與構件不滿足式(1)要求，其破壞處于彈塑性斷裂狀態[30-38]。而目前，由小尺寸金屬試樣的結構特性，來確定材料特性的研究還未見詳細報道。對于實際工程常見的含有不同長度裂縫的有限尺寸金屬結構，精確預測其結構的破壞荷載與過程等還有待改進。

綜上所述，由處于彈塑性斷裂狀態的小尺寸金屬試樣確定其材料參數，由確定的材料參數預測其結構破壞，目前仍是亟待解決而未圓滿解決的2個關鍵科學難題。由此，本文基于考慮試樣尺寸與裂縫相互影響的邊界效應基本理論[12-24]，發展建立了可描述金屬的塑性——彈塑性——線彈性斷裂等不同斷裂狀態模式的力學模型，嘗試將兩個獨立的金屬材料參數——強度與韌度聯系起來，從而建立起金屬的結構特性與其材料參數間的紐帶橋梁。

1 彈塑性斷裂力學理論及模型

1.1 基本理論

本文通過兩個極限準則——采用無限大板含有長裂縫情況對應的斷裂韌度KIC和未含裂縫試樣對應的屈服強度σY，來確定小尺寸金屬試樣的彈塑性斷裂狀態。

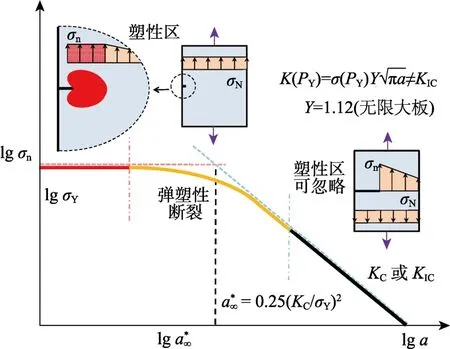
圖1 無限大板情況的斷裂破壞Fig.1 Fracture failure of infinite large plate

如圖1所示的無限大板斷裂，當試樣尺寸及初始裂縫都大于一定值，其裂縫尖端的塑性區影響可忽略，試樣受控于斷裂韌度準則(平面應力情況下的斷裂韌度KC或平面應變情況下的斷裂韌度KIC)；當裂尖的塑性區不能忽略，采用線彈性力學理論確定金屬材料的σY與KC的數值存在尺寸效應。

由經典線彈性斷裂力學理論可知[39-40]：

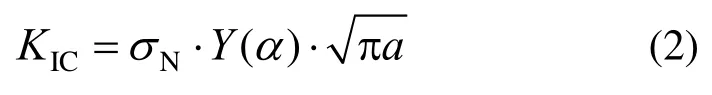
式中：σN為名義結構應力；Y(α)為幾何形狀參數；a為初始裂縫長度。

圖1中，韌度準則KIC和強度準則σY的交點記為定義為材料特征裂縫長度[12-24]，則基于式(2)可得：

Y(α)可由應力強度因子手冊查取，對于無限大板，Y(α)=1.12，則：

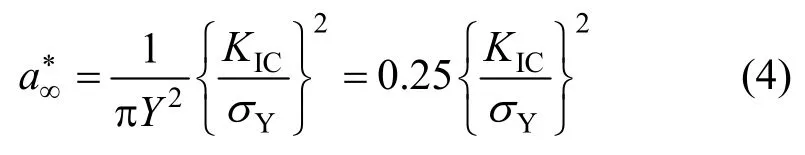
只與σY與KIC相關，則是材料參數。

由此，經典的線彈性斷裂力學表達式(2)可改寫為：

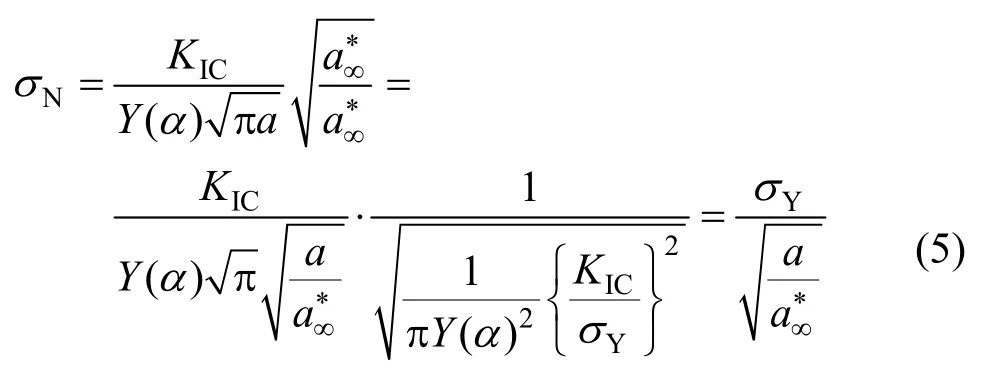
這里，a/＞＞1時，韌度準則發揮作用。

另外，重新考慮強度準則。如圖1所示，當強度準則發揮作用時，a趨于0，或a/＜＜1，則可得：

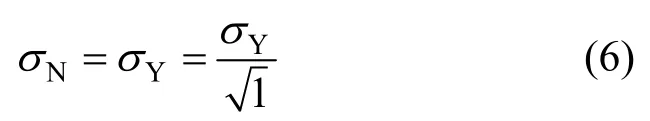
式(5)和式(6)可視為材料破壞的極限情況(分別對應于斷裂韌度準則KIC與強度準則σY)。將式(5)和式(6)合并, 即可得描述塑性——彈塑性——線彈性斷裂的模型計算表達式[12-24]：

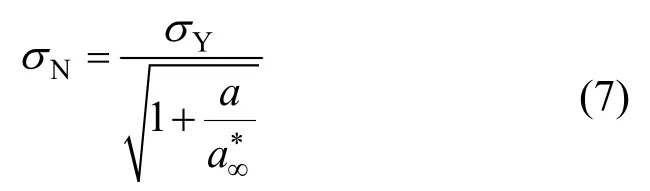
當a/≥10時，即a≥2.5(KIC/σY)2，式(7)蛻化為式(5)，破壞由斷裂韌度準則控制。當a/≤0.1時，式(7)蛻化為式(6)，破壞由強度準則控制。而當0.1＜ae/＜10，為彈塑性斷裂破壞。

1.2 基于有限尺寸試樣的結構特性確定其材料參數

對于實際工程中常用的有限尺寸試樣，可引入考慮初始裂縫影響的名義應力σn，其與σN滿足：

基于力與力矩平衡方程，可得單邊裂縫拉伸試樣(SENT)的其中縫高比α=a/W，W為試樣尺寸。

則線彈性斷裂力學計算表達式(2)可變化為：

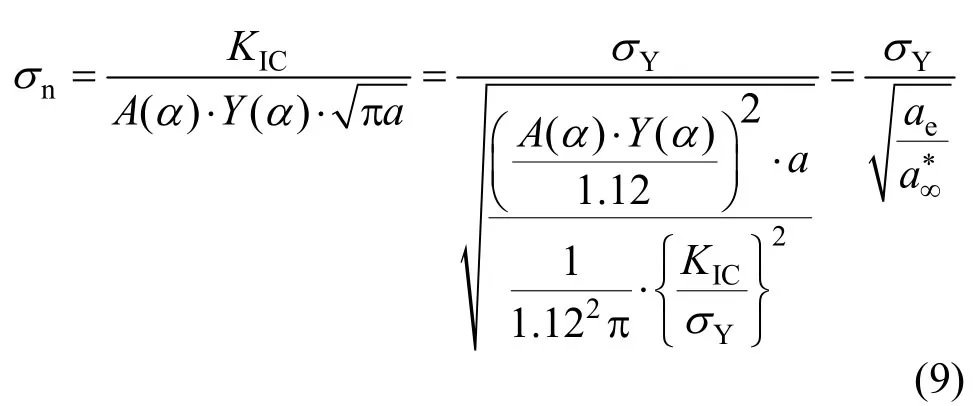
式中，引入有限尺寸試樣的結構參數ae：

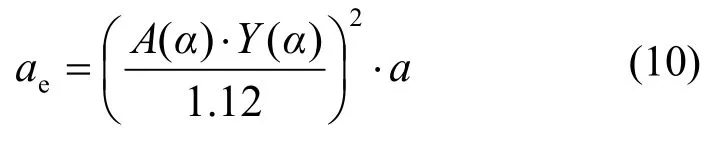
ae定義為結構等效裂縫長度，可見其只與試樣幾何、試樣型式等相關。

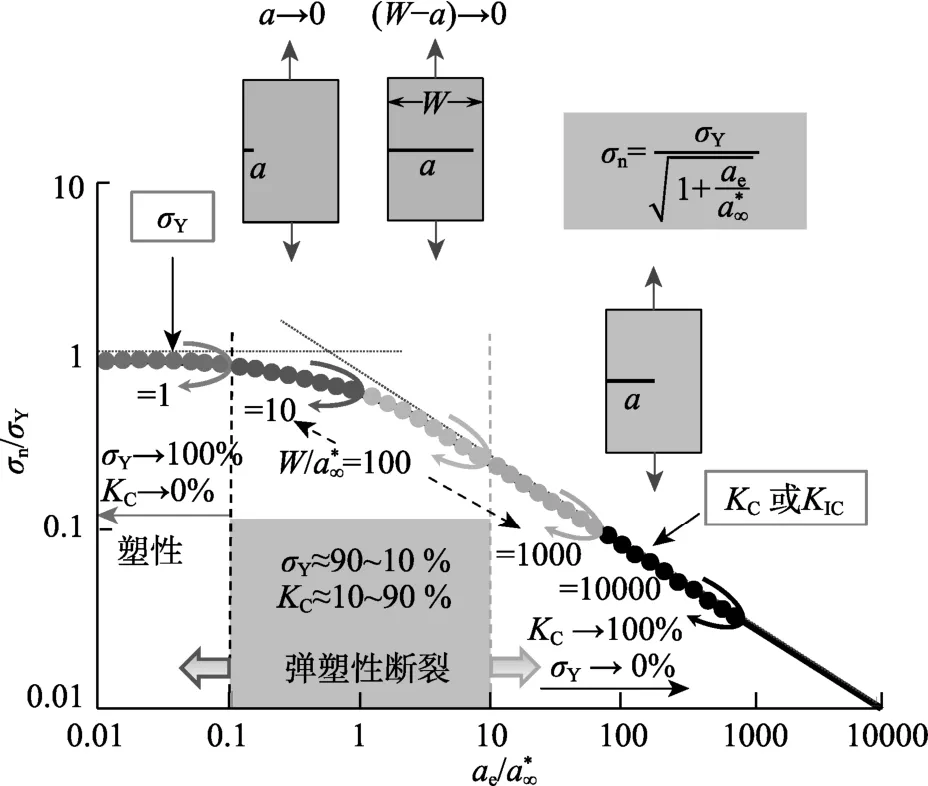
圖2 有限尺寸拉伸試樣的彈塑性斷裂Fig.2 Elastoplastic fracture of a tensile specimen with a finite size

進一步，將式(11)變換形式可得：

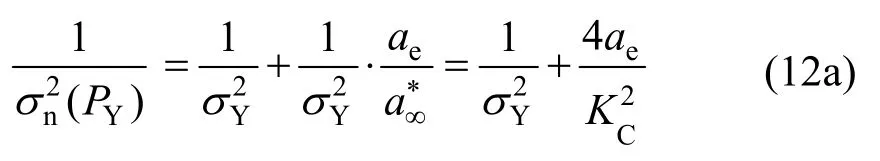
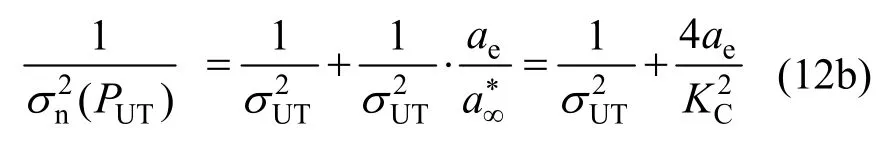
式中：PY為試樣屈服荷載；PUT為試樣極限荷載；σn(PY)為PY對應的名義應力；σn(PUT)為PUT對應的名義應力。

首先測試得到低合金試樣的PY或PUT，進一步計算出σn(PY)或σn(PUT)，再由式(10) 確定ae后，即可基于式(12)回歸分析確定出材料參數——斷裂韌度KC及屈服強度σY或極限強度σUT。

1.3 由材料參數預測結構特性

圖3展示了低合金類金屬材料的結構特性與材料特性的聯系。

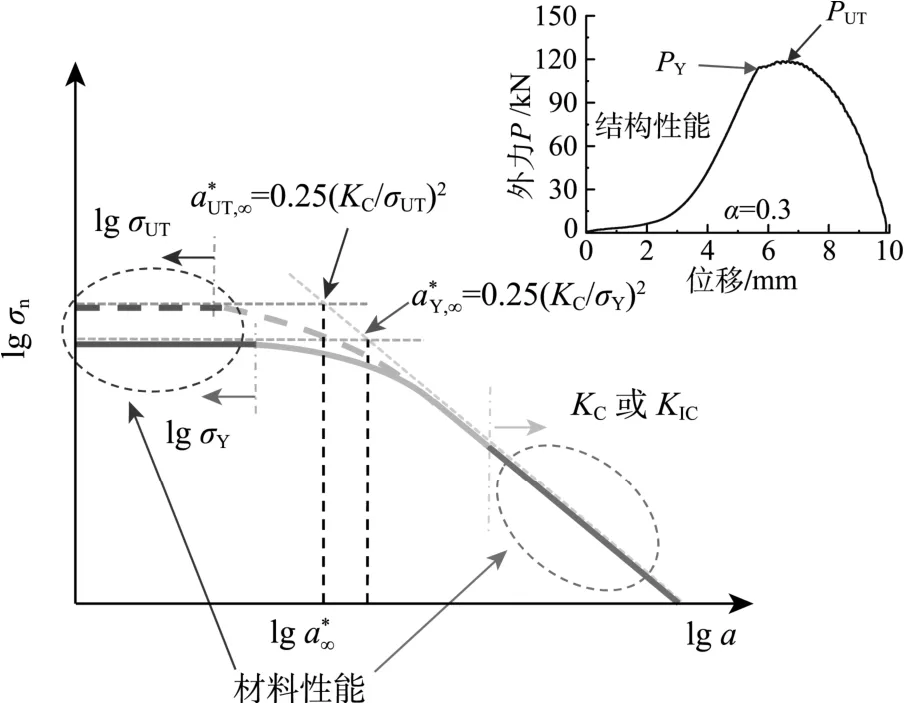
圖3 低合金的結構性能與材料性能的聯系Fig.3 Link between structural behavior and material properties of low-alloy high-strength steel

若已知有限尺寸試樣的結構特性(PY或PUT)，采用式(12)，外推確定材料參數—KC與σY(或σUT)。

若材料參數—KC與σY或σUT已確定，則可基于確定的材料參數(KC、σY或σUT)，采用式(11)，反演建立該金屬材料的破壞全曲線。對于具有不同預制縫長a的相同尺寸W的試樣；或者具有相同預制縫長a的不同結構尺寸W的試樣，其結構參數ae不同，因此具有個性化的結構特性。當已知實際金屬幾何結構參數ae(由式(10)確定)，則可基于該金屬材料的破壞預測全曲線，反解出該金屬結構的破壞荷載——PY或PUT，從而實現由材料參數預測個性化結構特性的目的。

2 試驗驗證

2.1 試驗設計與試驗加載

試樣所用材料選用安陽鋼鐵股份有限公司生產的Q345B型號的低合金高強度結構鋼。出廠檢測報告給出的該型號鋼材的屈服強度為515 MPa～520 MPa，極限強度為595 MPa～598 MPa，延伸率為26%，含碳量為0.16%，含硅、錳、磷、硫、鋁依次為0.16%、0.49%、0.011%、0.005%、0.013%。

采用相同尺寸W而不同裂縫長度a的Q345B鋼材單邊裂縫拉伸試樣，尺寸形狀如圖4所示。

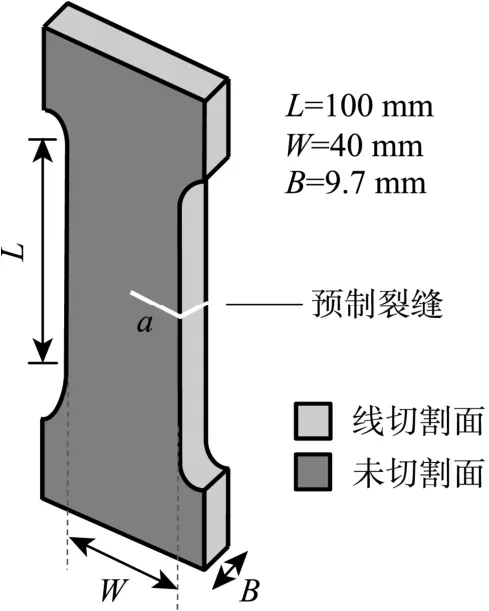
圖4 Q345B試樣的尺寸形狀Fig.4 Sharp of Q345B specimens

試樣的弧型段高度為20 mm，矩形夾持頭的尺寸為70 mm×80 mm，試樣有效長度L=100 mm，試樣寬度W=40 mm，試樣厚度B約為9.7 mm。試樣的縫高比α=a/W分別為0.1、0.2、0.3、0.4、0.5、0.6、0.7，每個縫高比對應制作5個試樣，共計7組35個試樣。試樣不需要進行疲勞試驗形成疲勞裂紋，而采用線切割工藝預制初始裂縫a。所用試樣實際尺寸見表1。試樣尺寸小于滿足線彈性斷裂的尺寸要求(式(1))。

試樣的拉伸試驗在SHT4605型600 kN電液伺服萬能試驗機上進行。如圖5所示，試驗機端部為固定夾頭，鋼板試樣端部固定。試驗按GB/T 228.1—2010等規范[41]中規定速率進行勻速加載至試樣斷裂破壞，加載速率為0.5 mm/min。試驗過程中記錄每個試樣的屈服荷載PY與極限荷載PUT。

圖5 Q345B試樣的試驗加載全景圖Fig.5 Loading panorama of Q345B specimens

典型的實測試樣的荷載-位移全曲線如圖6所示。實測各試樣的屈服荷載PY為與極限荷載PUT列入表1。試樣拉斷前后的形態見圖7。

2.2 約束情況下拉伸板的名義應力σn

圖8為考慮機器加載端約束的單邊裂縫拉伸試樣的應力分布示意圖[42-43]。外荷載P的作用線在試樣中心垂線，外力的增加使鋼板裂縫邊不斷張開，但由于加載端對拉伸試樣的強力固定，限制了試樣裂縫邊的變形，從而試樣產生了附加彎矩Mm。

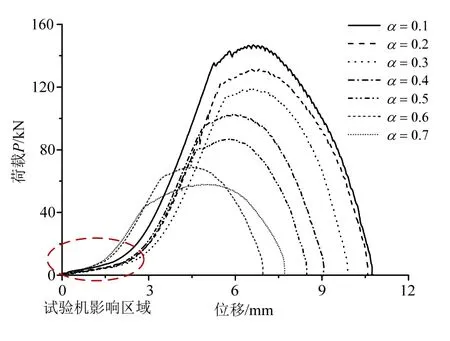
圖6 Q345B試樣的荷載-位移全曲線Fig.6 Experimental load-displacement curves of Q345B specimens

圖7 Q345B試樣拉斷前后形態Fig.7 Prepared Q345B specimens and their failure

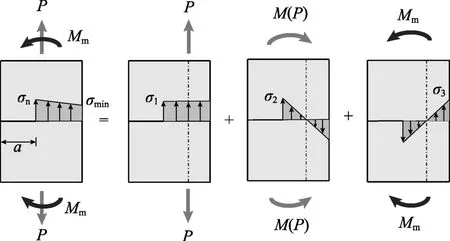
圖8 考慮機器加載端約束的拉伸試樣的應力分布Fig.8 Stress distribution of tensile specimen considering the constraint from test machine

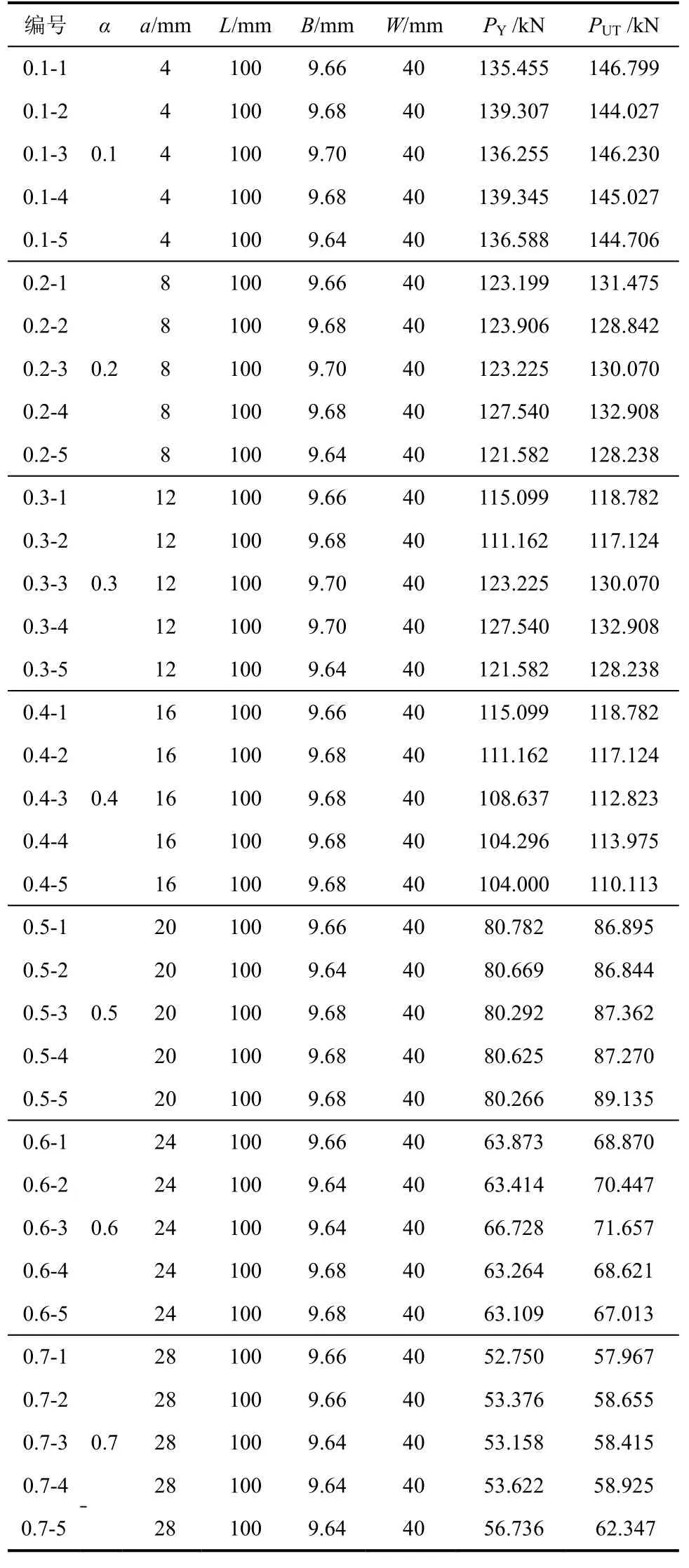
表1 實測Q345B試樣的屈服荷載PY與極限荷載PUTTable 1 Experimental PY and PUT of Q345B specimens

基于圖8受力情況，可得出考慮加載機器約束影響的金屬單邊裂縫應力強度因子中的幾何形狀參數Y(α)的具體計算式為[42-43]：

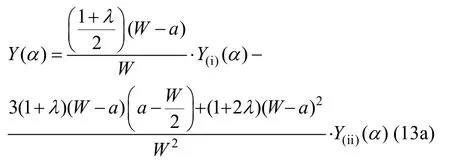
式中，λ為應力分布差異系數，λ=σmin/σn。在本文加載模式下，試樣裂縫邊張開較小，λ在0.95～0.85取值[42-43]。裂縫邊完全未張開的極限情況下λ=1.0。

圖9為對于有限尺寸金屬試樣，考慮其裂縫尖端塑性區影響的應力分布示意圖[42-43]。

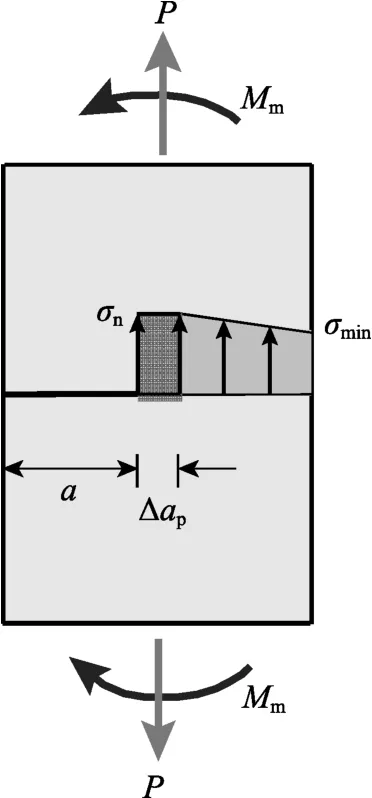
圖9 考慮有限尺寸金屬試樣的裂縫尖端塑性區的應力分布Fig.9 Stress distribution of finite-size metal specimen considering the plastic zone at the crack tip

記裂縫尖端塑性區為Δαp，由力的平衡可得：

由σmin=λ σn,P=PY，則：

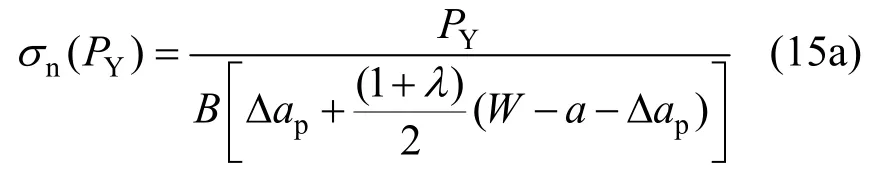
P=PUT，則：

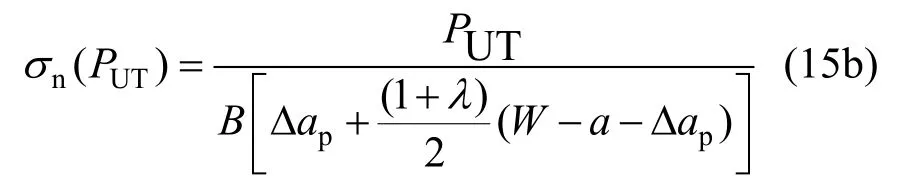
基于各試樣的實測屈服荷載PY或極限荷載PUT，由式(15)確定出各個試樣的應力σn(PY)或σn(PUT)；結合式(10)和式(13)計算每個試樣的幾何結構參數ae, 即可基于式(12)，回歸分析確定材料參數——斷裂韌度KC及屈服強度σY或極限強度σUT。

2.3 由屈服荷載確定Q345B的屈服強度與斷裂韌度

圖10展示λ=0.90,即σmin=0.90σn時，基于本文模型，采用實測PY確定Q345B鋼的材料參數——屈服強度σY、斷裂韌度KC和特征裂縫長度的情況。不同情況下確定的Q345B 鋼的材料參數詳見表2。

當假定σmin=σn，即λ=1.0的極限情況，確定的σY與平面應力條件下的斷裂韌度KC，都略低于考慮應力沿韌帶高度分布差異的λ＜1.0的情況，這點與文獻[42]的結論相一致。應力分布差異系數λ取0.95～0.85范圍，確定的σY與KC相差不大而較為接近。

本次試驗，相機拍攝的在試驗前、屈服及極限荷載時的試樣表面情況，如圖11所示。統計σY時的塑性區約為1.0 mm～2.0 mm。

如表2所示，λ＜1.0時，不考慮塑性區時(Δap=0.0)確定的σY略高于考慮塑性區(Δap=1.0 mm～2.0 mm)的情況；而KC略低于考慮塑性區的情況。

如表2所示，塑性區Δap取1.0 mm～2.0 mm時，σY=504.80 MPa～525.18 MPa，其平均值為516.25 MPa。可見，采用本文所提模型確定的屈服強度σY，與材料性能檢測報告值(σY=515 MPa～520 MPa)吻合良好。

值得說明的是，本文所用試樣并未對其表面進行拋光處理，更接近實際工程中取樣鋼材的真實情況。本文進行了與含裂縫試樣相同條件下的無縫試樣的拉伸試驗，其實測屈服應力值僅為355 MPa，遠小于檢測報告值(515 MPa～520 MPa)。可見，直接測試未拋光處理的無縫鋼材試樣，并不能得到其真實強度；而基于本文所提模型，采用小尺寸含預制裂縫試樣，可得到其真實強度。

表2 由P=PY確定的Q345B的材料參數Table 2 Determination of the material parameters of Q345B with P=PY

如表2所示，塑性區Δap取1.0 mm～2.0 mm時，KC=63.83 MPa·m1/2～70.76 MPa·m1/2，其平均值為66.14 MPa·m1/2。文獻[44]報道了美國AISI1040型號鋼材的平面應變條件下的斷裂韌度KIC=54 MPa·m1/2，該類型鋼材的屈服與極限強度分別為515 MPa和585 MPa，與中國Q345B鋼材的強度指標較為相近。考慮到平面應變條件下的斷裂韌度KIC要略小于平面應力條件下的斷裂韌度KC，因此，采用本文所提模型確定的KC=63.83 MPa·m1/2～70.76 MPa·m1/2較為合理。

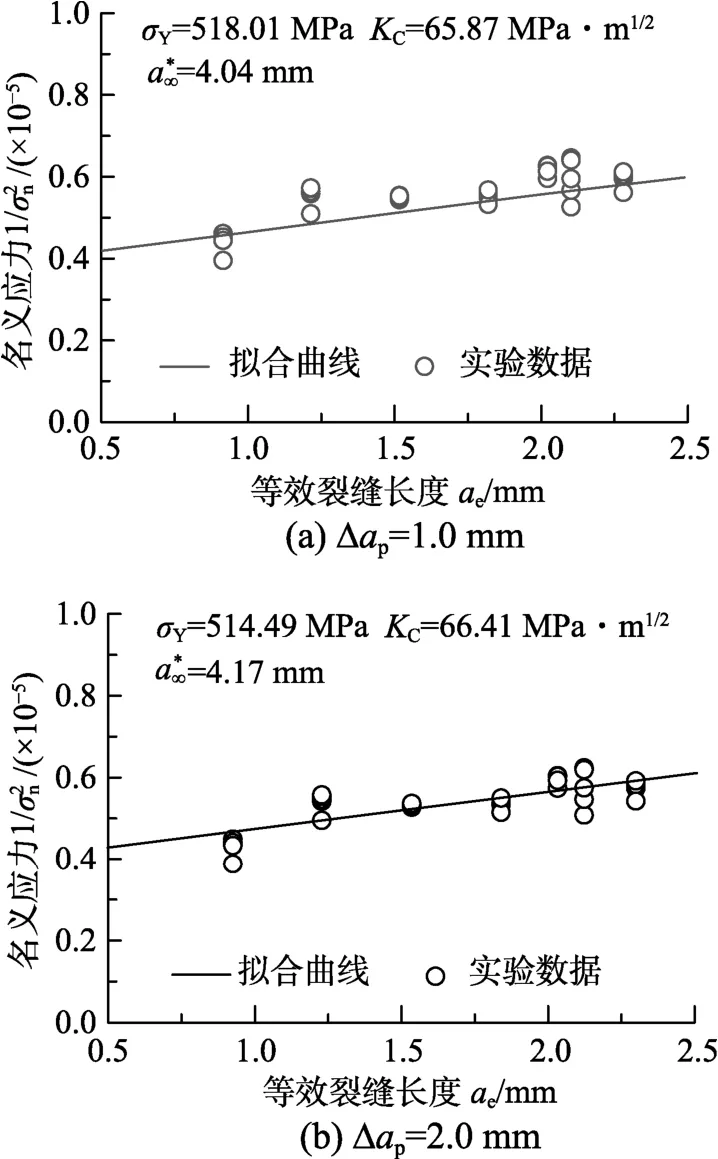
圖10 σmin=0.90σn時由PY確定Q345B的材料參數Fig.10 Determination of the material parameters of Q345B by using σmin=0.90σn and P=PY

圖11 試驗前、屈服荷載和極限荷載時試樣表面(a=4 mm)Fig.11 Surface of specimens before test, around PY and at PUT (a =4 mm)

2.4 由極限荷載確定Q345B的極限強度與斷裂韌度

對于金屬試樣，測試其極限荷載在普通試驗室條件下較易實現。而目前，采用極限荷載預測低合金高強度鋼斷裂韌度的方法還未見報道。

圖12為σmin=0.85σn時，基于本文所提模型，由實測極限荷載PUT，回歸分析確定Q345B鋼的材料參數—極限強度σUT、斷裂韌度KC和特征裂縫長度的情況示意。基于本文模型采用PUT確定的Q345B 鋼的材料參數詳見表3。

Q345B試樣的極限荷載時的塑性區應略大于屈服荷載時的塑性區；統計本次試驗通過相機連續拍攝量取的極限荷載時的塑性區約為3.0 mm～6.0 mm(如圖11)。如表3所示，塑性區Δap取4.0 mm～6.0 mm，σUT=576.82 MPa～593.80 MPa，其平均值為587.44 MPa；KC=63.83 MPa·m1/2～70.76 MPa·m1/2，其平均值為64.70 MPa·m1/2。采用本文模型確定的σUT，與材料性能檢測報告值(σUT=595 MPa～598 MPa)吻合良好。

仍需說明，本文進行了與含裂縫試樣相同條件下的無縫試樣的拉伸試驗，其實測極限強度值僅為518 MPa，遠小于檢測報告值(σUT=595 MPa～ 598 MPa)。

通過表2和表3的比較可見，由極限荷載PUT確定的斷裂韌度(平均值KC=64.70 MPa·m1/2)與由屈服荷載PY確定的斷裂韌度(平均值KC=66.14 MPa·m1/2) 基本一致，吻合良好。

表3 由P=PUT確定的Q345B的材料參數Table 3 Determination of the material parameters of Q345B with P=PUT

2.5 基于材料參數預測Q345B的結構特性

如圖13～圖16所示，若材料參數(強度與斷裂韌度)已知，可基于發展的模型(式(11))，建立起Q345B斷裂破壞全過程曲線。即由材料參數個性化預測結構特性；結合所提模型的由結構特性確定材料參數的功能，從而可建立材料特性與結構特性間的紐帶橋梁。

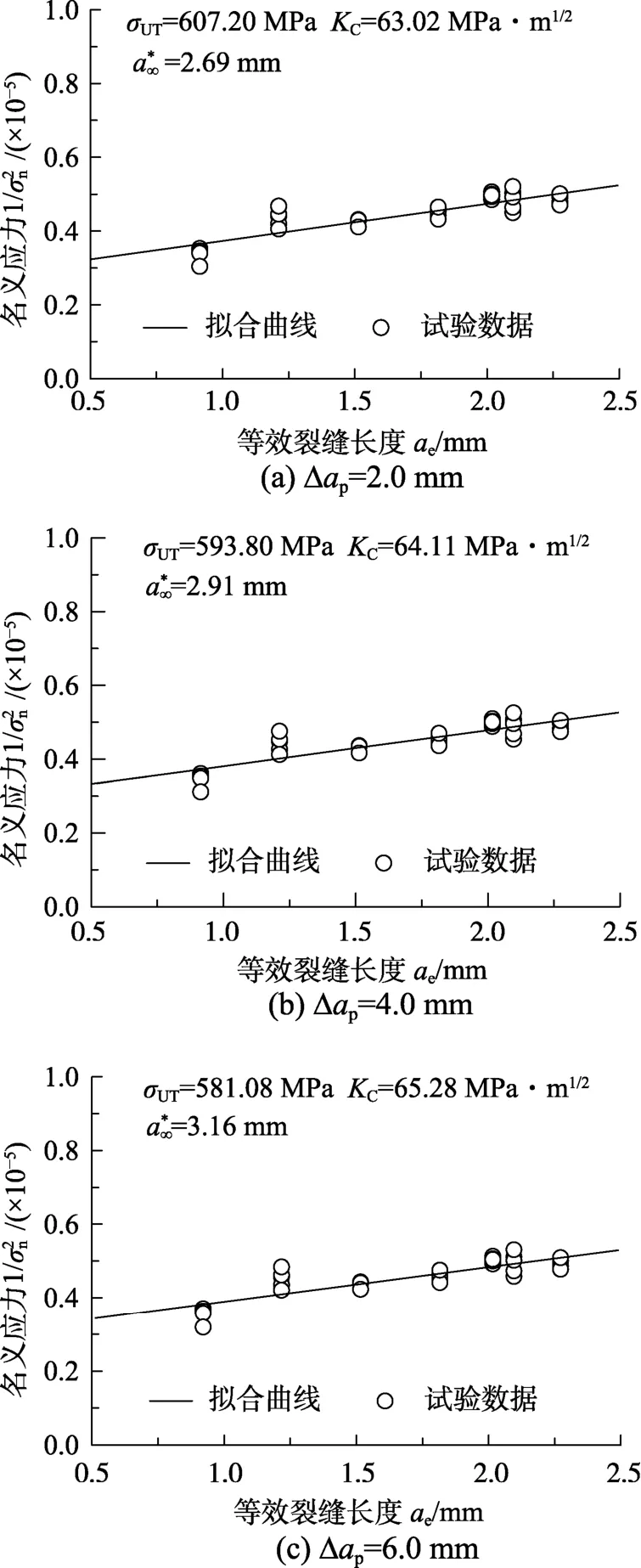
圖12 σmin=0.85 σn時由PUT確定Q345B的材料參數Fig.12 Determination of the material parameters of Q345B by using σmin=0.85σn and P=PUT

由圖13～圖16可見，本文Q345B試樣處于彈塑性斷裂狀態考慮試驗結果離散性導致的個性化結果，使材料參數變化±10%，對應的預測包絡曲線都可涵蓋全部的試驗數據。

作為預測全曲線的應用特例，可進行有限尺寸Q345B試樣的屈服和極限荷載的預測。

圖13 由材料參數σY =518.01 MPa和KC=65.87 MPa·m1/2確定的Q345B結構斷裂曲線Fig.13 Structural fracture transition of Q345B using materials constants σY =518.01 MPa and KC=65.87 MPa·m1/2

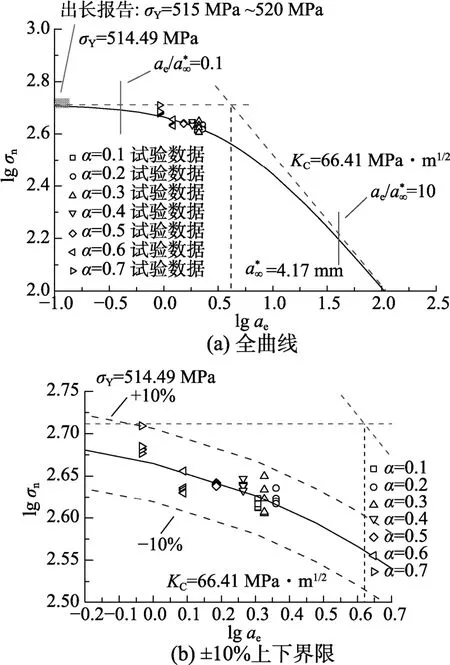
圖14 由材料參數σY =514.49 MPa和KC=66.41 MPa·m1/2確定的Q345B結構斷裂曲線Fig.14 Structural fracture transition of Q345B using materials constants σY =514.49 MPa and KC=66.41 MPa·m1/2

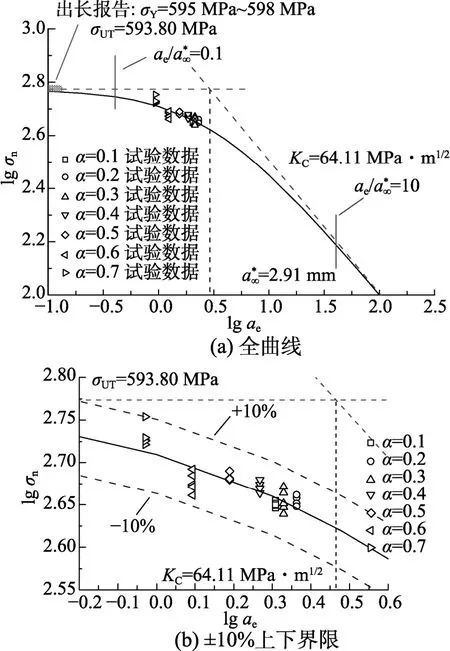
圖15 由材料參數σUT =593.80 MPa和KC=64.11 MPa·m1/2確定的Q345B結構斷裂曲線Fig.15 Structural fracture transition of Q345B using materials constants σUT =593.80 MPa and KC=64.11 MPa·m1/2

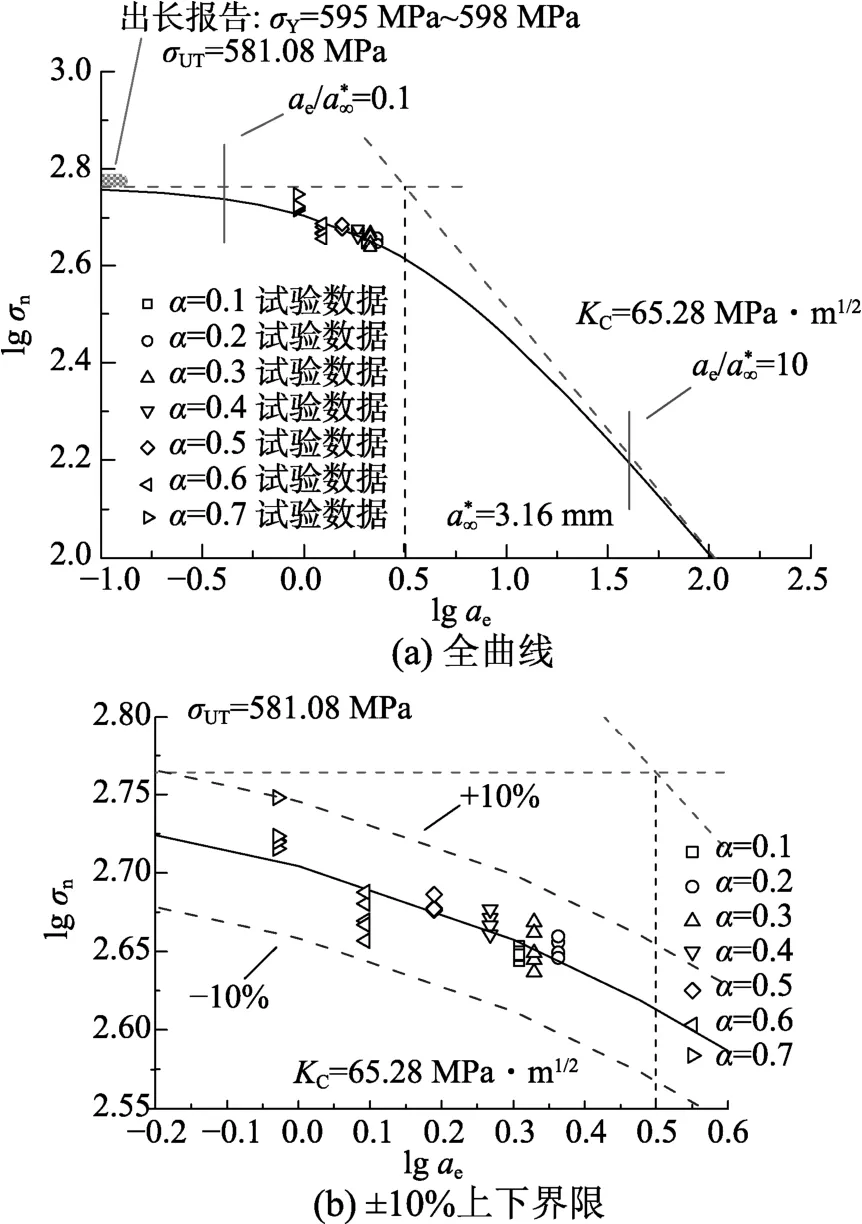
圖16 由材料參數σUT =581.08 MPa和KC =65.28 MPa·m1/2確定的Q345B結構斷裂曲線Fig.16 Structural fracture transition of Q345B using materials constants σUT =581.08 MPa and KC=65.28 MPa·m1/2

表4和表5分別為預測的Q345B屈服和極限荷載，與實測屈服和極限荷載的比較結果。其中，PY為實測屈服荷載；PY,c1為基于本文模型，由材料參數σY=518.01 MPa和KC=65.87 MPa·m1/2反演得到的屈服荷載值；PY,c2為由材料參數σY=514.49 MPa和KC=66.41 MPa·m1/2反演得到的屈服荷載值。PUT為實測極限荷載；PUT,c1為基于本文模型，由材料參數σUT=593.80 MPa和KC=64.11 MPa·m1/2反演得到的極限荷載值；PUT,c2為由材料參數σUT=581.08 MPa和KC=65.28 MPa·m1/2反演得到的極限荷載值。

由表4和表5可見，預測屈服與極限荷載與實測值吻合良好。

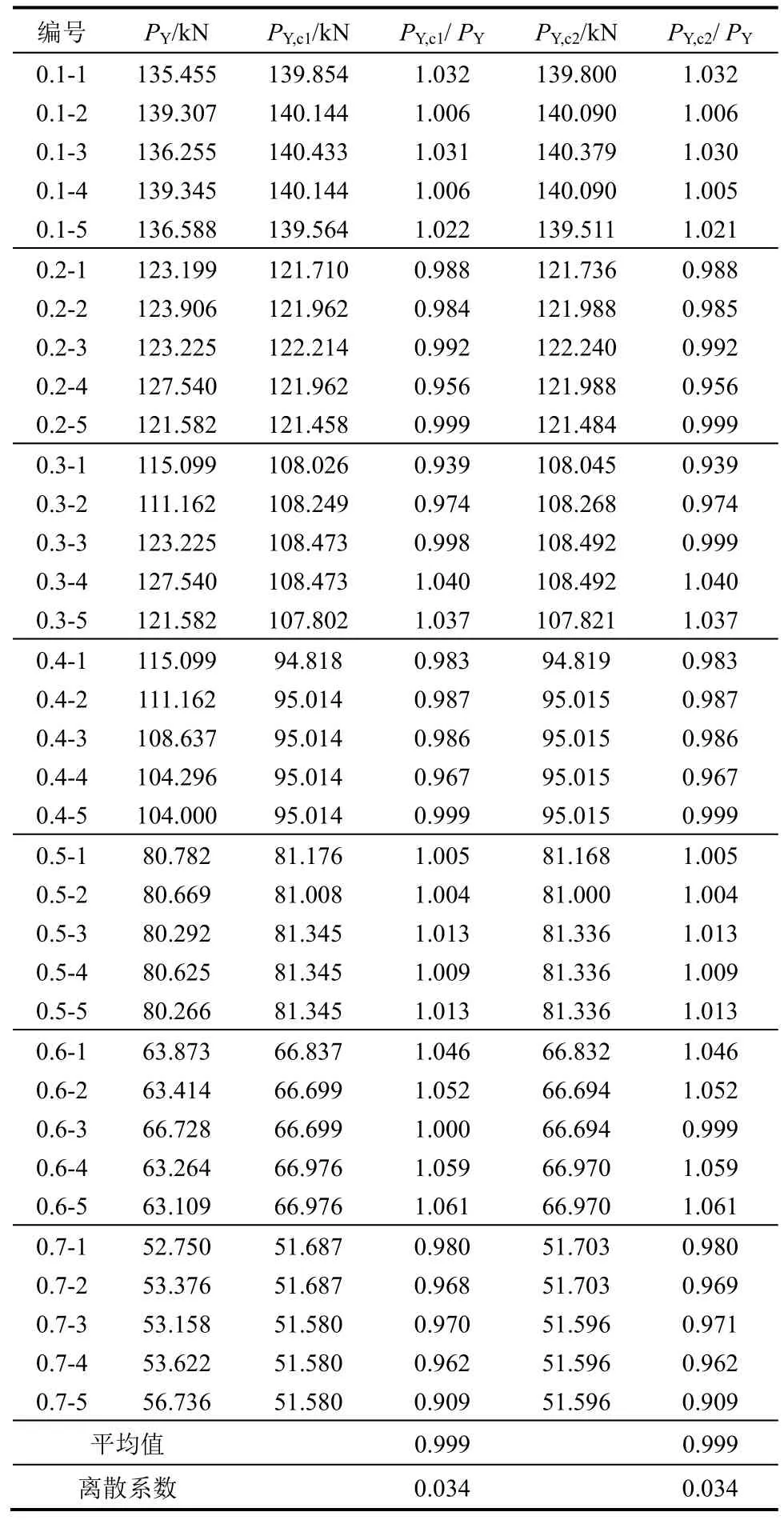
表4 預測 Q345B的屈服荷載與實測屈服荷載的比較Table 4 Predicted and experimental PY of Q345B specimens

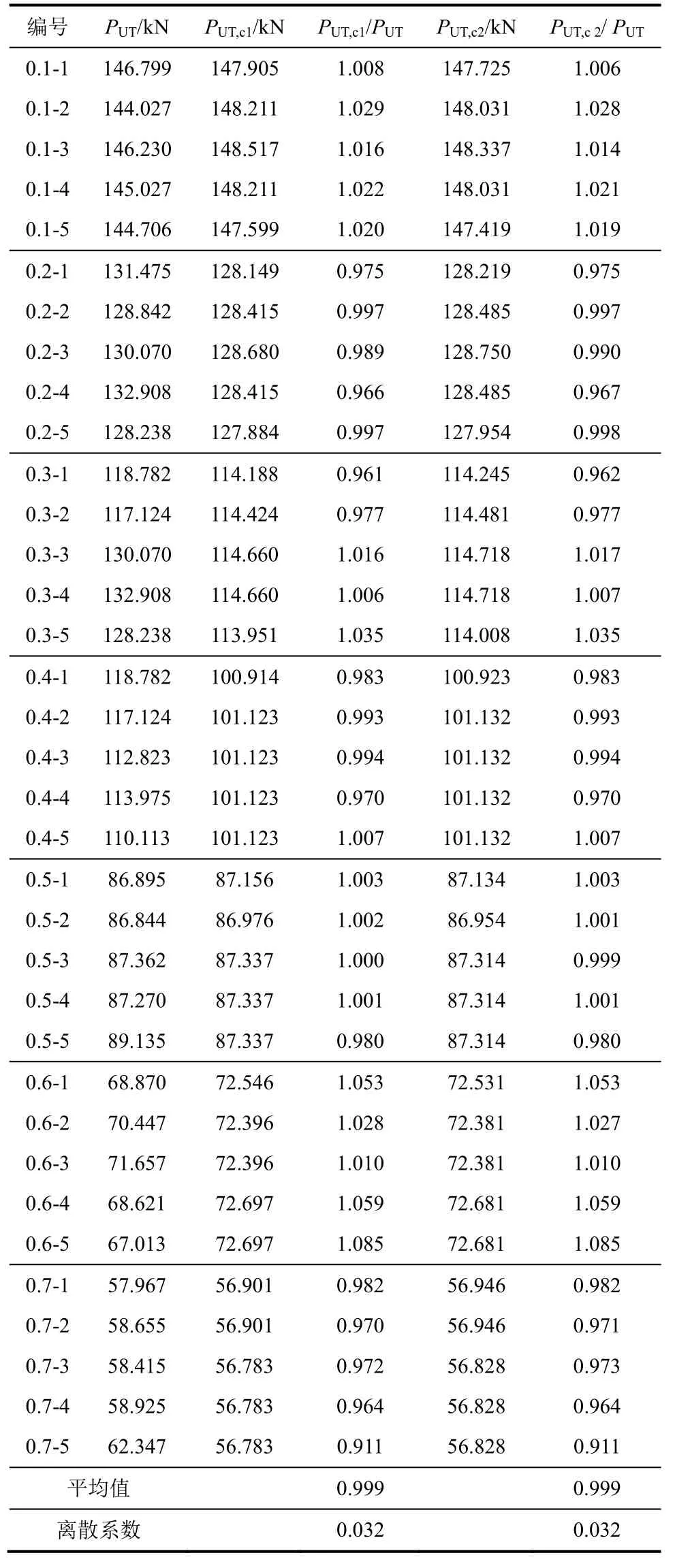
表5 預測Q345B的極限荷載與實測極限荷載的比較Table 5 Predicted and experimental PUT of Q345B specimens

3 結論

本文基于經典的線彈性斷裂理論，考慮了裂縫與試樣邊界的相互影響，發展了彈塑性斷裂理論與模型。將兩個獨立的材料參數——強度與斷裂韌度聯系起來，從而建立起金屬的結構特性與其材料參數間的紐帶與橋梁。由Q345B低合金結構鋼的單邊拉伸試樣試驗，驗證了所提理論與模型的合理性與有效性。本文研究的主要結論如下：

(1) 由處于彈塑性斷裂控制的、相同尺寸而不同縫高比的小尺寸金屬試樣的屈服或極限荷載，即可同時確定其材料參數——斷裂韌度、屈服或極限強度。分別由屈服和極限荷載確定的Q345B的平面應力情況下的KC相一致；試樣厚度約為9.7 mm的Q345B的KC=64.70 MPa·m1/2～66.14 MPa·m1/2。直接對未進行拋光等處理的無縫Q345B試樣進行拉伸試驗，并不能得到其真實強度；而基于本文模型，采用含預制裂縫試樣，可得到其真實強度及斷裂韌度。

(2) 基于確定的材料參數，可建立描述金屬材料的塑性——彈塑性——線彈性斷裂等不同斷裂狀態模式的破壞全曲線。考慮試驗結果的離散性，材料參數變化±10%對應的預測包絡線可涵蓋全部的試驗數據。基于確定材料參數，可對給定尺寸的Q345B試樣的屈服和極限荷載進行精確預測。

(3) 本文模型建議采用小尺寸單邊裂縫試樣進行拉伸試驗，不需滿足現有規范測定金屬斷裂韌度時對于試樣尺寸的嚴格要求；對于試樣裂紋的預制，不需進行疲勞試驗，只需采用線切割技術切縫。所提模型及應用方法計算簡便但有足夠精度，對應試驗易操作，因此便于在普通實驗室推廣應用。

需要說明的是，本文建立的彈塑性斷裂模型，除得到了本文Q345B低合金鋼的試驗驗證外，對于低碳鋼及鋁合金等其他金屬材料也同樣有效。