FLAC與極限平衡法聯合分析高陡礦山邊坡 穩定性的應用研究

柏樹豐

摘要：基于極限平衡法、強度折減法和重度增加等方法，結合巖土工程中現有邊坡計算和分析方法的特點，研究了強度折減法和極限平衡法的基本原理和適用條件。對于某礦山300m高陡邊坡，采用基于強度折減FLAC數值模擬方法和極限平衡法，分析兩種不同開挖方案下礦山高陡邊坡的穩定性，確定相應的邊坡穩定系數和最危險截面，為選擇合理的開挖方案提供依據。根據研究結果，通過FLAC數值模擬與極限平衡法得出的穩定安全系數，二者計算結果相近、最危險滑動面也類似;但是FLAC數值模擬可更精確、有效地模擬邊坡的塑性破壞和塑性流動，并可得到邊坡滑動體的形狀和位置。

Abstract： Based on the methods of limit equilibrium method， strength reduction method and weight increase， combined with the characteristics of existing slope calculation and analysis methods in geotechnical engineering， the basic principles and applicable conditions of strength reduction method and limit equilibrium method were studied. For a 300m high and steep slope in a certain mine， the strength-reduced FLAC numerical simulation method and limit equilibrium method are used to analyze the stability of the mine high and steep slope under two different excavation schemes to determine the corresponding slope stability coefficient and the most dangerous sections and provide a basis for selecting a reasonable excavation scheme. According to the research results， the stability safety coefficient obtained by FLAC numerical simulation and limit equilibrium method is similar， and the most dangerous sliding surface is similar; but FLAC numerical simulation can more accurately and effectively simulate the plastic failure and plasticity flow of the slope， and the shape and position of the slope sliding body can be obtained.

關鍵詞：高陡礦山邊坡;極限平衡法;有限差分法;穩定性

Key words： high and steep mine slope;limit equilibrium method;finite difference method;stability

中圖分類號：U416.14? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2020）03-0188-03

0? 引言

邊坡穩定性問題目前是土木工程和采礦領域的熱點問題。目前，較為重要的分析方法包括強度折減、重度增加和極限平衡等研究方法。其中，作為一種應用廣泛的計算研究手段，極限平衡[1-4]基于莫爾—庫倫強度準則，能較為準確地得出邊坡發生危險性滑動的范圍，在邊坡領域中有非常多的應用實例。但極限平衡條分法[1]忽略了土體的本構關系，在一定條件下，其結果與實際邊坡的受力情況有一定的出入;強度折減法原理是假設邊坡達到極限破壞狀態，并且在此狀態下，計算得出邊坡安全穩定系數，即邊坡強度的儲備安全系數，該法得出的安全系數與Bishop極限平衡法得出的結果類似，是一種通過折減塑性巖體抗剪強度參數的計算分析方法;而重度增加法與上述兩種方法有所不同，其具體計算過程時設定巖體抗剪強度為恒定常數，逐漸增加重力加速度，對巖體的塑性進行數值研究計算，直至邊坡達到極限破壞狀態，最后根據重力加速度與實際重力加速度的比值，得出在邊坡超載條件下的安全儲備系數。對于巖土工程的塑性問題，常用的計算方法還有有限差分計算法、有限元分析法、有限差分計算法及設定邊界元法等。針對復雜邊界和任意幾何形狀的塑性巖土體問題，目前大多數研究方法都可以通過模擬巖土體結構及內部相互作用進行空間狀態下的三維數值計算。但強度折減法較傳統平衡條分法，其運用的有限差分計算理論更具發展前景，其研究范圍及適用性也更廣。

本文應用有限差分軟件FLAC軟件[2]與極限平衡法對某礦山高陡邊坡的兩種開挖方案及其相應的穩定安全系數進行了對比分析，并對礦山該邊坡開挖方案做出評價。旨在為FLAC與極限平衡法在高陡礦山邊坡穩定分析的應用提供一定的理論基礎，并為確定高陡邊坡開挖方案提供參考依據。

1? 數值分析計算原理

1.1 強度折減法原理

根據現有研究，強度折減法是用相同的約束折減系數F，來重新定義土力學中兩個重要強度指標粘聚力c、內摩擦角？準，從而計算出一組折減后的粘聚力c′和內摩擦角？準′，并且在邊坡應力穩定狀態下，利用有限差分數值理論計算法反復計算至邊坡臨界破壞狀態，得出強度指標與原始巖土體強度指標的比值，即為該邊坡安全系數Fs。采用強度折減法所確定的安全系數Fs可由以下公式表示，即：

1.2 極限平衡法原理

邊坡穩定分析的極限平衡法是以Mohr-Coulomb強度準則為理論基礎，將邊坡滑移面劃分為數個垂直的巖土條塊，分別對各個條塊進行經典力學受力分析，得出極限平衡狀態下整個巖土體的安全穩定系數[3]。巖土體的穩定安全系數Fs是巖土體沿滑裂面的抗剪強度τf與巖土體沿滑動面滑移時實際所產生剪應力τ之比，即： （3）

極限平衡法要求每個條帶都要遵循靜力學平衡條件及Mohr-Coulomb強度準則理論，以使整體滿足上述條件。但此法建立的數學計算模型是在非靜定條件下，并不能直接求得邊坡安全系數。在利用極限平衡分析法計算邊坡穩定性時，得出的穩定安全系數應滿足：①條塊之間分界面必須符合巖土破壞的破壞準則（條塊之間相互作用的內力遵循莫爾—庫倫強度準則，也就是說，條塊間切向力兩側豎直面上的平均剪應力不超過分界面巖土體的平均抗剪強度）;②在條塊間無拉應力這兩個條件下，需對某些多余未知量如條塊間內力假定或平衡條件進行一定假定，才能使非靜定問題變為靜定可解。瑞典條帶法，也稱瑞典圓弧滑動法，認為滑動面是圓柱形狀，并忽略兩側的力;Bishop法作為一種經典的極限平衡法，假定兩相鄰條塊間切向力為零;Janbu普遍條分法[4]預先假定條塊之間存在合力點并假設其具體位置;在不平衡條件下也存一些推力傳遞計算法，例如Sarma、Morgenstern—Price、Spencer等方法，它們認為是在相鄰條帶之間的界面上，有法向與切向條間力夾角，并且條塊之間的內力合力也在分界面上。

2? 高陡礦山邊坡穩定性分析

2.1 工程概況

滇中一礦山呈東西走向，礦區內巖系寒武系下統梅樹村組作為區域內主要的巖系，它占總巖系50%之上，具體地質分布從南至北，分別是震旦系、寒武系、泥盆系，其中第四系主要集中于礦帶邊緣處。礦區礦體整體賦存較淺，開挖表面巖層后，即可展開系統的露天開采。依據礦山整體生產計劃，剝離表面覆蓋巖層后，在礦體東部會形成高達300m的邊坡，依據礦山實際生產需要及邊坡穩定性要求，初步設計兩套開挖方案，方案一的最終邊坡角為38°，方案二最終邊坡角為35°。

依據《巖土工程勘察規范》（GB50021—2001），該礦山300多米高邊坡開挖工程屬一般邊坡工程，相應設計穩定系數可取1.15至1.30。但鑒于邊坡開挖過程的爆破振動影響以及邊坡開挖安全問題將直接影響到礦體開采的順利推進，為完善邊坡開挖設計，并為礦山開采提供設計依據，需對開挖方案以及開挖所形成的邊坡穩定性等做出合理評價。

2.2 FLAC數值分析邊坡穩定性

2.2.1 模型與計算參數

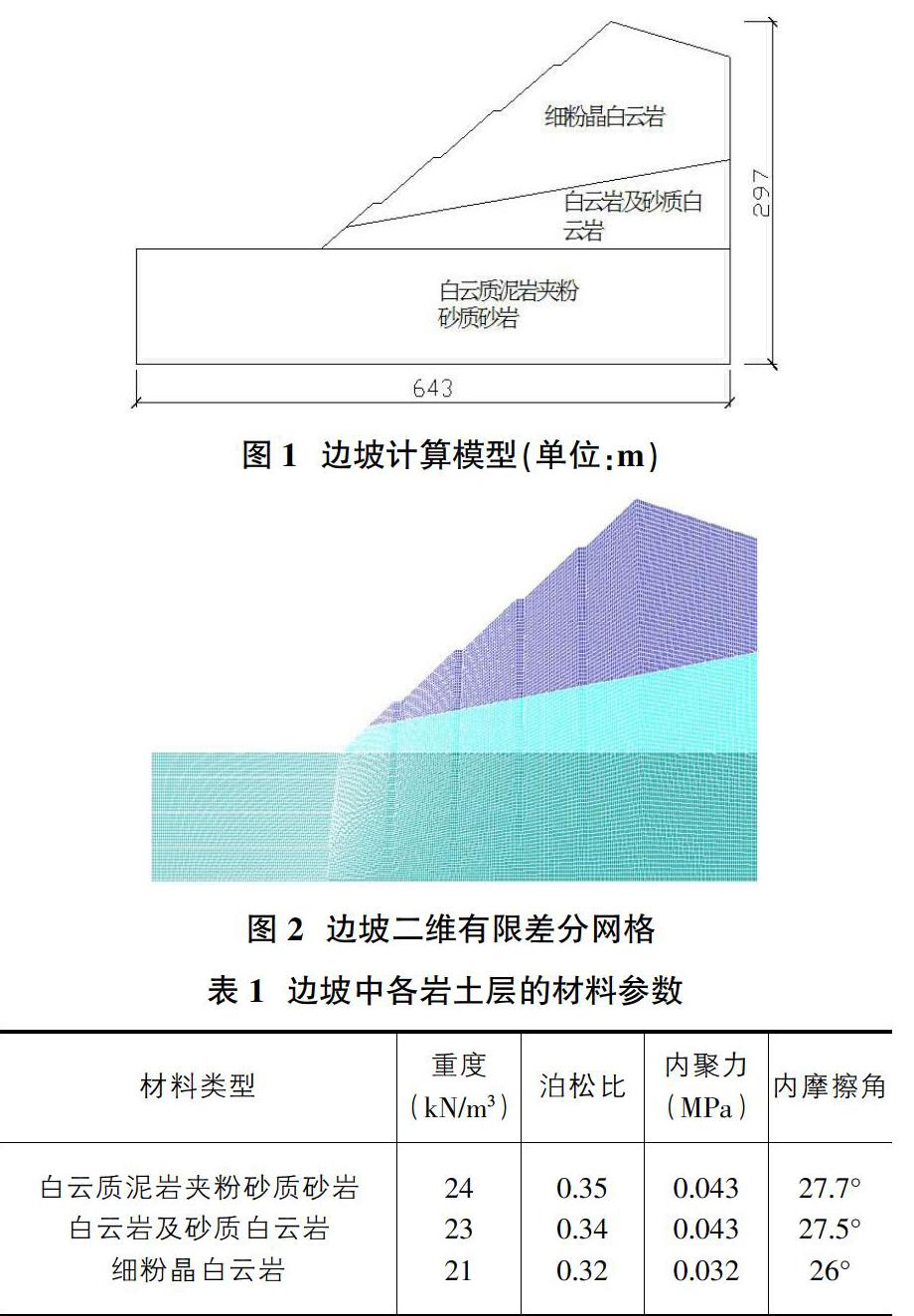
根據礦山邊坡現場地質勘察資料，選取邊坡一典型剖面進行穩定性計算分析，將該典型剖面簡化為平面應變問題并建立邊坡穩定性分析平面模型。建模中，考慮到材料分區情況，邊坡的縱向長度為643m，高度為297m，邊坡平面模型、巖體材料分區及有限差分網格見圖1和圖2。邊坡穩定性分析所用的巖石力學參數按勘查分析結果取值，邊坡內各巖性材料的具體巖石力學參數見表1。

在上述邊坡穩定性計算分析模型中，x方向右方向為正，y垂直上方為正，賦予計算模型底部和側向水平方向各一個約束，同時賦予上部為自由邊界[5]。在具體邊坡穩定性研究計算過程中，只考慮重力作用，取重力加速度為9.81m/s2，假定y軸負方向為正。此外，由于勘察表明該邊坡地下水位埋深較深且在邊坡開挖范圍內均不存在地下水，因此建模時不考慮地下水對邊坡穩定性的影響因素。

2.2.2 計算結果與分析

采用FLAC-Slope軟件，基于強度折減法計算了兩種初步開挖設計方案下礦山300m級高邊坡的穩定性。在方案一數值計算分析中，總位移較大的速度矢量分布于部分邊坡范圍，方向指向坡面臨空面，計算得出穩定性系數為1.11，具體計算結果如圖3、圖4所示;在圖4中，當折減系數值為1.11時，邊坡的剪應變增量形成類似于滑弧的形狀，且貫通坡頂到坡腳。由此可知，在1.11的折減系數下，邊坡穩定性急劇下降，邊坡將沿著剪應變增量最大的位置產生滑動破壞。開挖方案二計算結果如圖5和圖6所示。方案二計算結果與方案一類似，但是由于邊坡坡度的改變，邊坡的穩定系數從1.11提高至1.2。

由圖3至圖6可以看出，合理改變邊坡體的幾何形狀，可大大改善坡體的內應力分布，減輕坡體的自重壓力，從而增加坡體穩定性。

2.3 極限平衡法分析邊坡穩定性

基于上述邊坡穩定性計算分析模型和巖石力學參數，應用極限平衡法對上述300m級高邊坡在兩初步開挖設計方案下的穩定性進行計算分析[6]，計算時同樣不考慮地下水的作用。鑒于組成邊坡的材料其物質成分相對較均勻，Bishop法考慮穩定性失穩滑動面形狀為圓弧形以及條間合力作用點位置，且簡化計算分析較方便，適用于圓弧形滑面破壞并較符合高陡礦山邊坡實際情況[7]，因此本文采用Bishop法分析高陡礦山邊坡的穩定性。

圖7顯示了邊坡劃分條塊和方案中最危險的滑動面，計算得到開挖方案一情況下的邊坡穩定安全系數為1.143;圖8顯示了在開挖方案二中，邊坡劃分塊最危險的滑動面，計算得出邊坡穩定安全系數為1.254。從圖7與圖8可以看出，極限平衡法計算得出的最危險剖面滑動面與FLAC計算結果相似，且二者計算得到的穩定安全系數相差不大，兩方案在采用極限平衡法與FLAC時的計算誤差分別為2.9%和4.3%。由圖7和圖8的計算結果同時可知，在極限平衡條件下，方案一計算得出的穩定性安全系數不滿足《巖土工程勘察規范》中邊坡設計穩定系數應取1.15～1.30的要求。

3? 結論

①FLAC數值模擬計算分析法和極限平衡分析計算法在研究邊坡穩定性時，兩種計算最終結果差異不大，兩開挖方案在采用極限平衡法與FLAC時的計算誤差分別為2.9%和4.3%，最危險滑動面類似。

②與極限平衡法相比，由于FLAC數值模擬方法考慮了巖體內部的本構關系，模擬了實際邊坡的塑性流動性與塑性破壞過程，并得出了邊坡滑動面位置及滑移體形狀，故FLAC數值模擬計算結果更為精確。

參考文獻：

[1]王建良，姚激，蒲秀榮.軟巖邊坡穩定性的FLAC和剛體極限平衡法對比分析[J].科學技術與工程，2009，9（16）：4693-4697.

[2]周瑞龍，鐘豫.FLAC軟件在某露天采場邊坡穩定性分析中的應用[J].現代礦業，2016（8）：46-47.

[3]楊明瑞，楊寶強，馬立秋.基于極限平衡理論和有限元強度折減法的預應力錨索加固邊坡穩定性分析研究[J].土木工程，2017，6（5）：515-524.

[4]楊明成，康亞明.容重增加法在邊坡穩定性分析中的應用[J].哈爾濱工業大學學報，2009，41（6）：187-190.

[5]白潤才，王志鵬，王喜賢.基于FLAC3D軟件的露天礦邊坡穩定性分析與研究[J].露天采礦技術，2013（8）：1-2，5.

[6]王恩華，江俐敏，羅浩.巖土工程計算軟件FLAC3D基本原理與在工程上的應用[J].城市建設理論研究，2014（12）.

[7]龍浪波，王鷹.FLAC在宜萬鐵路某隧道洞口段邊坡穩定性分析中的應用[J].鐵道勘察，2009，35（5）：77-80.