基于非軸對稱吻切技術的三維激波逆向乘波設計

張濤 鄭曉剛 湯祎麒 李怡慶 尤延鋮

摘要：基于傳統吻切理論，本文提出了一種非軸對稱吻切技術，并在此基礎上，完善了傳統二維特征線技術，可對復雜三維曲面激波進行逆向求解。通過事先指定三維激波曲面形狀，根據氣流方向與激波曲面當地曲率方向，能夠求出各離散激波點對應的離散微吻切平面。以該微吻切平面與激波曲面的交線作為各微吻切平面內的激波形狀，利用已知激波求解流場的二維逆向特征線法對各微吻切平面的流場進行求解，隨后將各離散微吻切平面內獲得的壓縮型線進行組合，獲得能夠生成指定復雜三維曲面激波的壓縮型面。研究結果表明，基于非軸對稱吻切技術的三維激波逆向求解方法能夠很好地求解出生成指定三維激波曲面的乘波構型，激波形狀吻合度較高；運用該逆向設計方法求解獲得的截面流場信息與數值模擬結果相似度較高，其流場分布表現出相同的規律，但在增壓比的預測上存在一定的誤差，主要集中在遠離對稱面三維效應明顯處，最大誤差約為8.4%，可見該逆向乘波設計方法的精度基本滿足要求。另外，針對特定的二次錐面激波方程，設計截面內激波曲線越高，乘波體的升阻比越低。

關鍵詞：非軸對稱吻切技術；特征線；乘波體；升阻比；逆向設計

中圖分類號：V211.3文獻標識碼：ADOI：10.19452/j.issn1007-5453.2020.11.005

基金項目：國家自然科學基金（51276151，91441128）；基礎科研項目（B1420133058）；中央高校基本科研業務費（20720140540）；江西省教育廳科技項目（GJJ190523）

近空間飛行器的設計和開發是目前國際航空航天領域的研究熱點，同時也是各國競相爭奪空間技術的焦點之一[1-5]。盡管國內外大量學者就此類問題進行了詳細的研究，但是仍然存在一些亟待解決的問題。其中飛行器的升阻力特性因其直接決定了飛行器的氣動性能，并且通過傳統的設計方法很難構造出具有高升阻力特性的飛行器機體，因此該問題長期以來受到國內外學者的廣泛關注。區別于亞聲速流動，超聲速流動最顯著的特征在于流場中存在激波，流場中的激波一方面給飛行器帶來了額外的激波阻力，但另一方面，氣流經過激波后能夠實現減速增壓的特點，從而為飛行器部件中需要高壓的區域提供合適的氣流，如飛行器機體下表面或吸氣式推進系統的內流通道等。

利用超聲速流動具有激波的優勢，Nonweiler[6]首次提出運用二維斜激波波后流場設計飛行器機體，該機體前緣產生的斜激波能夠完全附著于機體下表面，從而抑制下表面氣流于機體邊緣處上洗至上表面導致升力缺失，較好地解決了飛行器升阻力的問題。該設計方法被命名為楔導乘波理論，生成體即為楔導乘波體。運用類似的理論，乘波理論的激波形狀由最初的斜激波[7]發展至圓錐激波、橢圓錐激波等三維回轉激波生成體，基于該方法生成的乘波體即為錐導乘波體[8]，錐導乘波理論在很大程度上拓寬了乘波理論的應用范圍，但由于激波形狀較固定，使得該理論仍然存在著較強的約束。為解決以上問題，Sobieczky[9]等提出了吻切錐導乘波理論，該理論將激波的平面形狀離散成激波微元段，每段微元均可根據當地曲率半徑獲得相應的圓錐激波，從而拓寬了乘波理論在激波形狀方面的限制，使得任意曲率中心連續過渡的激波曲線均能作為生成乘波體所需的激波曲面。

經過長期的發展，乘波理論已經逐漸趨于成熟，近年來國內外學者逐漸將重心轉移至乘波體氣動性能的優化[10-12]、乘波體與推進系統的一體化[13-17]等問題。作者認為，雖然各類乘波理論經過長期的發展已經基本趨于完善，但在實際工程運用中仍然存在著許多約束，其中最重要也是最難解決的問題仍然是傳統乘波設計理論，特別是吻切乘波理論在激波形狀設計中的局限性。傳統吻切乘波理論在設計過程中首先給定的是設計截面內的激波形狀，通過截面激波形狀可反向推導出該激波曲面的三維結構，因此，激波曲面的三維形狀是無法預先設計的，而是根據激波的截面形狀與激波生成體唯一確定。此外，在實際工程應用中，受到激波曲線的形狀約束，設計前緣型線時通常會遇到較強的約束，這主要是因為吻切乘波體設計理論中，前緣型線必須位于激波曲線的曲率中心與曲線之間，若前緣型線超越激波曲線曲率中心則無法構造乘波體下表面。因此，發展一套基于任意復雜三維激波曲面的氣動反設計方法從而進一步拓寬乘波理論的適用范圍，是亟待解決的關鍵問題。

氣動反設計的本質是預先給定激波反求激波生成體的過程，基于二維有旋特征線法，國內外學者開展了大量的二維氣動反設計研究，包括給定二維激波形狀反向求解壓縮型面[18]，給定壓力分布反求壓縮型面[19]以及給定馬赫數分布求解壓縮型面[20]等。以上研究較全面地解決了二維環境下的反設計問題，但是對于三維復雜激波的求解目前公開文獻較少，一些學者嘗試使用三維特征線法對其進行逆向求解[21-22]，但由于特征線法的復雜性以及三維求解過程中特征線易相交等問題，未能很好地解決三維激波曲面逆向求解的問題。

基于以上分析，在傳統吻切乘波體理論基礎上，本文進一步發展了基于非軸對稱吻切技術的乘波體設計方法。不同于常規吻切乘波理論，該方法將三維激波曲面在橫向上進行離散的同時，在流向上也離散為若干微小平面，本文將其命名為微吻切平面。利用改良后的二維逆向特征線法對各微吻切平面的流場進行求解，進而組合各微吻切面內的型線，獲得能夠生成指定復雜三維曲面激波的壓縮型面。本文針對不同的三維激波曲面，構建了三種乘波構型，對比其激波形狀與流場信息，用于驗證本文所述逆向求解技術的可行性和正確性。為了便于對比，在本研究中，乘波體前緣型線的二維形狀均指定為直線。針對激波方程為二次錐面的情況，本文探討了設計截面內激波曲線高度對乘波體升阻特性的影響。

1非軸對稱吻切技術

1.1吻切流基本原理

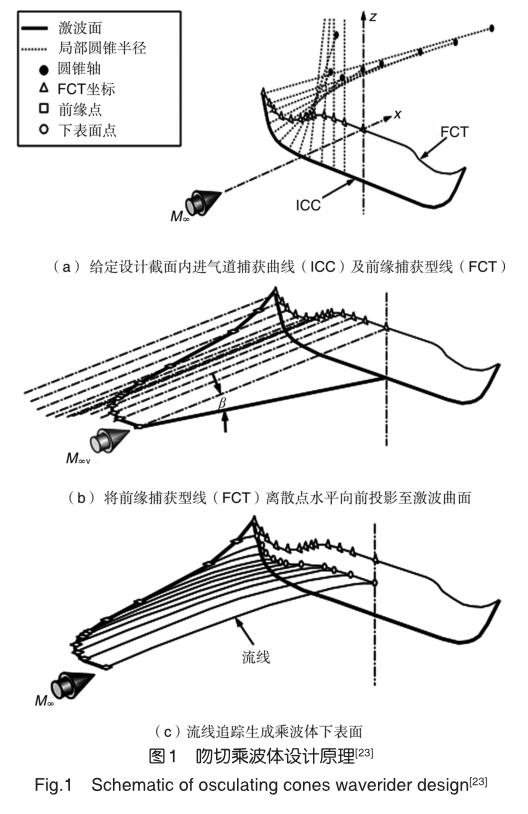
吻切乘波理論由Sobieczky[9]等于1990年率先提出。該理論認為：一般三維超聲速的運動方程都可以在二階精度范圍內用一個軸對稱流的運動方程來逼近。這個軸對稱的軸線位于通過該點流線的吻切平面（osculating plane， OP）內。于是，當地的三維流動就能夠由局部的二維流動（軸對稱流動也是二維的）來描述。在吻切面中，非軸對稱的激波后流動處理為錐形流。在出口平面內，沿激波曲線使用一系列吻切面來定義，每個吻切面內激波角為常數，以保證展向的連續性，而每個面中的錐形流頂點則由激波角和當地的曲率半徑確定。因此，此技術可將完整的激波形狀分解成一系列半徑不同的圓錐形激波“切片”，而激波后的流場則為一系列錐形流場的耦合流場。由此可見，錐導乘波理論只是吻切乘波理論的一個特例：錐形激波相當于吻切方法中半徑固定為一恒定值的情況。圖1給出了吻切乘波體的設計原理圖，圖中ICC為進氣道捕獲曲線，FCT代表前緣捕獲型線。

1.2非軸對稱吻切技術

直接對三維曲面激波進行逆向求解顯然是極為復雜的，因此需要進行降維處理，將三維的求解過程簡化為二維過程。參照吻切流理論，本文將三維曲面激波在橫向上進行離散，進一步地在流向上也離散為若干微吻切平面，在各微吻切平面內對激波曲線進行二維的逆向求解。本文將其命名為非軸對稱吻切技術，并認為一般的三維超聲速流動可由這些微吻切平面內二維流動的耦合來近似。該技術的核心問題是如何離散三維曲面激波得到一系列微吻切平面，本文將采用步進法根據前一點所得數據逐步對流場進行離散和逆向求解。基于非軸對稱吻切技術的三維激波逆向求解過程可分為4步（見圖2）。

（1）設計激波曲面的形狀，提取該激波曲面的方程

激波作為超聲速流場具有的最顯著的特征在很大程度上影響著飛行器及推進系統的氣動性能，對于外流部件，保證激波封閉飛行器下表面抑制上洗流能夠實現飛行器的高升阻力比特性。而以同樣的方式將推進系統的進氣道進口封閉能夠有效提高進氣道流量捕獲能力，從而進一步增加發動機提供的推力。因此激波的形式與分布方式的研究是實現超聲速飛行的關鍵。分析乘波理論的設計過程可以發現，無論是二元楔導乘波理論、錐導乘波理論，還是具有較高任意性的吻切錐導乘波理論，在設計之初均為預先指定激波的分布形式。然而三者在設計過程中均存在著局限性，即僅在某一截面（設計截面）內構造激波曲面的二維幾何形狀，隨后假設流動沿流向為平面流動（楔導乘波）或標準圓錐流動（錐導、吻切乘波）進行求解，對于三類乘波理論，其激波的二維幾何形狀分別為直線形、圓形和具有二次連續特征的曲線形。因此，乘波理論對激波三維形狀的考慮顯然是不充分的，從另一個角度分析，乘波理論實際上放棄了激波曲面三維特征這一自由度。

對于本文的研究，激波曲面的設計不再局限于某一平面，而是對全流場所具有的激波形狀進行設計。理論上任意滿足設計要求的三維曲面方程均能作為預輸入激波曲面。需要說明的是，激波曲面沿流向和橫向的曲率方向，也就是曲率的正負決定著氣流的壓縮方式（軸對稱外壓縮或軸對稱內壓縮），針對以上兩種壓縮方式求解過程顯然是不同的，由于求解過程的復雜性，本文暫不將曲率方向發生變化的激波曲面作為研究對象。因此，激波的設計過程需保證激波曲面各點的曲率方向相同。而曲面方程的確定對于求解特征點的曲率半徑顯然是必需的。

（2）設計物面前緣型線的三維構型

為保證所生成物面邊緣不產生溢流以提供較高升阻比，在前緣型線的設計中需要保證前緣型線與激波曲面相交。因此在已獲得激波曲面的前提下，前緣型線的三維構型將由其橫向投影形狀或流向投影形狀唯一確定。若在橫向截面內設計前緣型線則將其沿流向投影至三維激波曲面，若在流向截面內設計則將其沿橫向投影至三維激波曲面，從而獲得前緣型線的三維構型。隨后將三維前緣型線離散與三維激波曲面共同作為逆向求解的輸入條件。

（3）求解前緣離散點對應初始微吻切平面，運用逆向特征線法解得該微吻切平面的壓縮型線

初始微吻切平面可根據來流方向與對應激波點的法矢量唯一確定。如圖2（a）所示，本文將藍色箭頭所表示的氣流方向矢量與An點對應法矢量（normal vector）構成的平面定義為初始微吻切平面，該微吻切平面與給定激波曲面相交能夠獲得如圖2（a）中AnB所示的初始激波微元段。本文假設若An點與B點之間間距足夠小，則能夠將復雜的三維流動簡化為二維軸對稱流動。該假設在后續的數值模擬驗證中將得到證實。獲得以上條件后，運用基于激波曲線的逆向特征線法能夠較容易地求解出所需的壓縮型線，如圖2（a）中AnD所示。

（4）求解后續微吻切平面及對應壓縮型線，運用相同的方法獲得全流場參數

通過步驟（3）獲得了初始微吻切平面內的流場參數，為后續流場求解提供了可能。初始微吻切平面之后的微吻切平面不再將來流流動方向作為構造依據，而是由上一微吻切平面內最后一條左行馬赫線（圖2（b）中DB）與激波點B對應的法矢量唯一確定，考慮到后續微吻切平面的流動將主要受前部已擾動來流的影響，這是本文提出的非軸對稱吻切技術對吻切乘波理論在流動方向上的主要發展。前文分析中指出吻切平面將三維流動在周向內離散成軸對稱流動從而解決了三維流動的簡化求解問題，本文進一步拓展，將復雜三維流動在周向和流向內同時離散從而實現對更加復雜的三維流動的簡化求解。流向流場求解思路將在下一節沿流向曲率中心可變的逆向特征線法中進行詳細的分析。

將以上方法同時運用于其他離散前緣點（如圖2中An-1，An+1），并將離散流場進行三維組合后完成復雜三維流場的逆向設計。

2沿流向曲率中心可變的逆向特征線法

實現三維激波逆向求解的另一核心手段是逆向特征線方法（method of characteristic， MOC），運用該方法的逆置激波點過程能夠在二維環境內有效求解出指定激波所需的壓縮型面。傳統的二維特征線法多為正向求解，以來流條件為初始參數，以壓縮型線為邊界條件，根據已知兩點發出的異簇特征線，聯立特征線方程和相容性方程求解特征線交點的參數，最終獲得整個流場信息。而逆向特征線法的求解思路則與之相反，先給定來流參數和預想激波形狀，再采用特征線法逆向求解壓縮壁面型線的幾何位置參數，將后驗的參數變成可設計的參數。換言之，利用逆向二維特征線法可以根據所需的激波形狀反設計得到能夠產生該波系結構的壓縮型面幾何構型，但該逆向求解方法顯然無法實現任意三維曲面激波的求解，為此本文發展了一種沿流向曲率中心可變的逆向特征線法，該方法將在下文進行詳細研究。

特征線法是一種求解雙曲型偏微分方程的精確步進型方法。在定常超聲速流場中，由于其控制方程為雙曲型偏微分方程，流場中任一點的流動具有僅取決于上游流場中有限區域的性質，因此可以使用特征線法求解該流場。所謂特征線是指沿著該曲線積分將偏微分方程簡化為易于求解的全微分相容性方程。在超聲速流場中由于馬赫線就是特征線，因此可將控制方程簡化為以下兩個全微分方程組。特征線方程組：

通過聯立特征線方程組和相容性方程組求解特征線交點的參數，最終可獲得整個流場信息。

由于特征線理論具有較高的求解精度與較短的求解時間，長期以來被廣泛運用于超聲速領域的飛行器設計問題。此外，基于該理論，一系列逆向求解方法也得到了發展。其中包括給定壁面壓力分布求解超聲速流場、給定壁面馬赫數分布求解超聲速流場以及給定激波曲線求解超聲速流場等問題。針對本文的研究內容，給定激波曲線逆向求解超聲速流場將成為主要的實現手段。傳統的給定激波反向求解軸對稱超聲速流場的求解原理如圖3所示，可以發現，圖中具有兩條橙色曲線，其中平行于x軸的橙色虛線為軸對稱流場的回轉中心。其求解過程首先需要確定來流條件與預設計激波曲線形狀（圖3中紅色實線所示）并獲得激波起始點An，然后將該激波曲線離散為一系列微元段（如圖3中AnB、BB），進而運用特征線理論的逆置激波點過程求解激波點B處的左行馬赫線并與起始點An發射的流線相交得到壁面點D的初始值，隨后使用校正迭代法對D點進行修正直至精度滿足要求。同理可對下游點D進行求解進而求解整個超聲速流場，在此不再贅述。

傳統的給定激波求解流場的特征線程序能夠很好地實現二維流動或準二維流動（軸對稱流動）的精確求解，但該理論對于三維流動的求解顯然是不適用或者不精確的，其本質的原因在于各激波離散點的曲率中心受到三維效應的影響發生了變化。圖4為圓錐曲面與橢圓錐曲面沿程各激波點曲率中心分布對比，顯然圓錐流動的求解可以完全依賴于二維特征線法，但該方法無法滿足具有三維效應的橢圓錐流場的求解。無法求解的內在原因在于圓錐曲面與橢圓錐曲面沿流向曲率中心位置的不同。

對于圓錐曲面（包括母線為曲線的曲錐面），曲面上各點對應曲率中心均落于回轉軸線上，即曲面的物理中心與曲率中心重合，因此流場在周向位置內存在相似性能夠滿足二維流動對軸對稱流場的求解要求，然而對于橢圓錐曲面，曲面上各點的曲率中心不再落于某一軸線，而是由當地曲線曲率決定，因此不存在周向相似的特點，無法使用傳統的特征線法進行求解。經過以上分析可以發現，兩類流動的本質區別是曲率中心的問題，進一步而言是曲率半徑的問題，因此若在特征線法的求解中引入曲率半徑這一變量將有望解決特征線法解決三維流動的問題。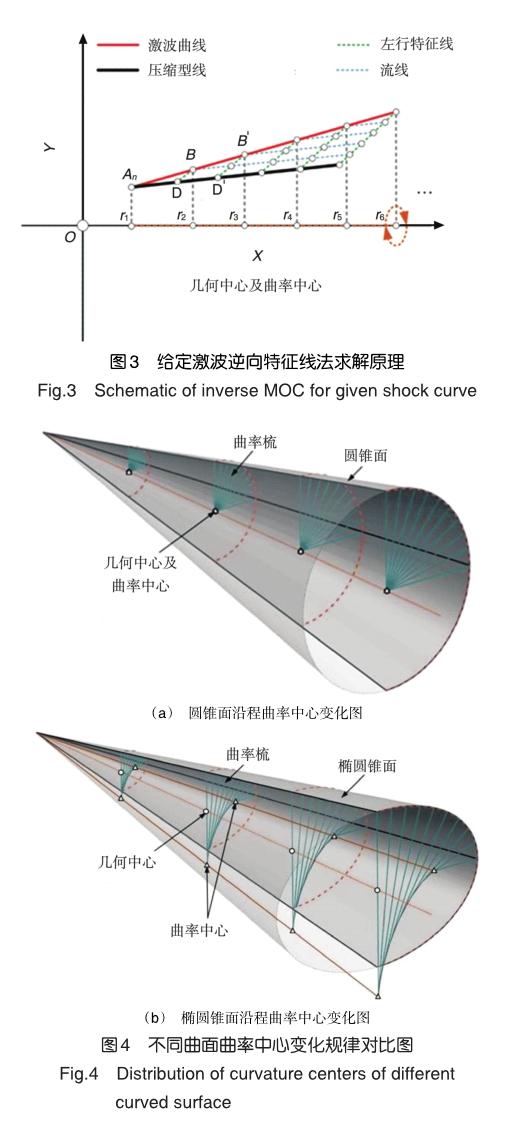

結合曲率半徑的變化，本文進一步發展了二維特征線理論，得到如圖5所示的曲率中心可變逆向特征線求解原理。求解過程首先需要獲得離散激波點當地曲率半徑，由于三維效應，該曲率中心將偏離回轉中心（圖5中X軸），且向下游偏離程度逐漸增大，故將呈現出圖5中橙色實線所示的偏離趨勢，該趨勢在圖4（b）中橢圓曲面的曲率中心分布中也有同樣的體現。曲率半徑的不同對應特征線求解公式中即為y值的不同，分析式（5）可以發現當y值趨于0時流動為標準的軸對稱流動，而當y值趨于無窮時流動將向二維流動轉變，因此當y值落于0與無窮之間時求解的流場為具有曲率半徑為y的圓臺的軸對稱流場（即前緣起始點不為原點），該流動將介于二維流動與軸對稱流動之間。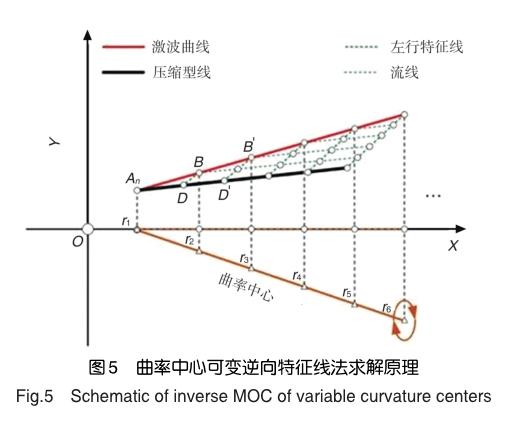

上述對y值分析仍然是針對曲率中心固定的流場求解，對于類似圖4（b）所示的變曲率中心流場的求解則需要在各個微元段內多次運用特征線法的以上特點，以圖5為例，求解激波微元段AnB流場時，以An點對應曲率半徑作為y值帶入特征線方程，而當求解BB時對應y值將采用B點的曲率半徑，隨后以相同的思路對下游流場進行求解獲得能夠滿足類似圖4（b）中所示的變曲率中心流場的逆向求解。上述曲率半徑選擇方式能夠成立是因為對于超聲速流動，氣流參數僅受上游參數影響，因此當微元段足夠小時以微元起始點的曲率半徑作為微元段的曲率半徑進行求解是可行的。此外，需要說明的是，圖5中所示的求解過程對應于圖4（b）中橢圓曲面短軸對應母線的求解，該母線沿流向曲率半徑逐漸增大，曲率中心偏離物理中心程度也同時增大，因此流場將出現沿流向趨于二元流動的趨勢。而對于長軸對應母線，觀察圖4（b）可以發現沿程各點曲率中心雖然偏離物理中心，但是其偏離方向與短軸對應母線相反，因此流場沿流向將更加趨于圓錐流動，即呈現出比“圓錐流動更圓錐”的流動特點。

因此，本文提出的基于非軸對稱吻切技術的三維激波逆向求解方法的實質是指在利用非軸對稱吻切技術對三維激波進行離散的每張微切面內，采用曲率中心可變的逆特征線法求解流場。

3復雜激波曲面逆向求解對比分析

本節將對上文所述的基于非軸對稱吻切技術的三維激波逆向求解方法進行實例分析，并與數值模擬結果進行對比分析以驗證該方法的正確性與可行性。需要特別指出的是，本文驗證逆向求解方法正確性的步驟為：首先設計三維激波生成體，隨后運用計算流體力學（CFD）對其進行求解，進而提取所具有的激波曲面進行對比驗證。因為運用CFD求解獲得的激波曲面存在一定厚度，故在提取激波曲面時將不可避免地存在誤差。

構造三維激波曲面時，本文采用圖6所示的一般錐面方程作為初始輸入。如圖6所示，過定點且與定曲線相交的所有直線構成的曲面稱為錐面，其中定點稱為頂點，定曲線為錐面的準線，構成錐面的每一條直線叫作母線，而準線所在的截面則稱作設計截面即為乘波體的結尾截面。因此，給定頂點坐標與準線方程即可獲得錐面方程。值得注意的是，橢圓錐實際上是頂點為坐標原點，準線方程為橢圓方程的特殊錐面。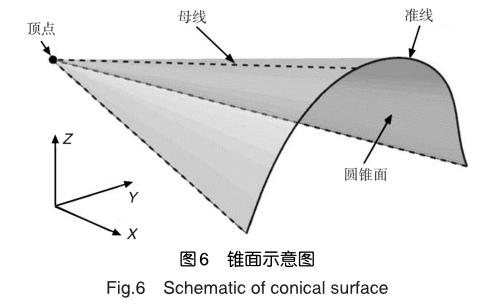

根據上述錐面定義，本文選取了三種錐面方程，并將乘波體前緣型線的二維形狀指定為直線，構建了三種不同的乘波構型，用以對比激波形狀及流場信息。三種不同錐面方程及乘波體設計的具體參數見表1。其中模型A與模型B的激波曲面實際上為橢圓錐面，而模型C的激波曲面在設計截面中的方程是二次曲線，因此，該錐面又稱為二次錐面。

在來流馬赫數Ma=6，H0=27km的條件下，根據前緣捕獲型線與預先給定的三維激波面方程，運用基于非軸對稱吻切技術的逆向求解方法便可獲得乘波體的下表面及其流場信息。

本文使用ANSYS Fluent求解基于有限體積法的歐拉方程來驗證基于非軸對稱吻切技術的三維激波逆向乘波設計方法的準確性。選擇基于密度的求解器來進行無黏計算。對流矢量選擇二階AUSM格式，CFL數設定為0.5以確保計算的穩定性。假設來流氣體為理想氣體，定比熱比γ為1.4。對于邊界條件而言，將乘波體壁面均設置為絕熱無滑移固體壁面。計算域入口選用壓力遠場邊界條件，出口設置為壓力出口邊界。網格方面，使用ICEM對乘波體流場劃分結構化網格，在乘波體壁面布置C型網格，在壁面和激波位置附近均進行網格加密處理，各算例網格數目均在350萬左右。

圖7為模型A乘波體結尾截面激波示意圖。其中左半為通過數值模擬獲得的乘波體結尾截面激波形狀與預設計截面激波形狀（圖中黑色虛線所示）的對比圖，右半為乘波體的俯視圖。此外，圖7左半上圖表示基于非軸對稱吻切技術，采用傳統的特征線法求解得到的結果，左半下圖表示特征線求解技術引入曲率中心變化獲得的結果。對比可以發現，在引入曲率中心變化之前，數值模擬得到的激波形狀與預設計激波形狀存在較大差異。而考慮曲率中心的變化之后，能夠很好地求解出生成指定橢圓錐激波曲面的乘波構型。該結論驗證了沿流向曲率中心可變的逆向特征線法的正確性，并實現了非軸對稱吻切技術在三維流場中的應用。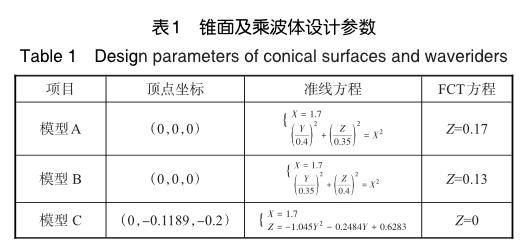

除橫向截面激波形狀，在流向截面內，本文所述逆向求解技術同樣表現出了較高的精度。圖8分別提取了模型A的4個流向截面（Y=0，Y=0.2，Y=0.4，Y=0.6）內的激波形狀與設計結果進行對比，其中紅色實線為預設計激波形狀，黑色實線為逆向求解獲得的壓縮型線，藍色實線為基于該壓縮型面運用數值模擬方法獲得的流向激波曲線。可以發現，藍色激波曲線基本被預設計的紅色激波曲線覆蓋，僅在某些局部位置出現微小偏差，該現象說明在流向截面內逆向求解方法能夠很好地復現預設計的激波形狀，求解精度基本能夠滿足要求。

圖9為模型B數值模擬結果與預設計激波形狀對比。可以發現，逆向求解結果與數值模擬結果同樣具有較高的相似度。模型A與模型B的激波曲面均為橢圓錐面，但不同于模型A，模型B的結尾截面激波形狀所具有的曲率中心顯然已經超越前緣捕獲型線，即激波曲線與曲率中心位于前緣型線的同一側。因此，運用已有的吻切乘波設計理論顯然無法獲得具有圖9所示激波形狀的乘波構型，這是因為乘波理論成立的客觀條件是前緣捕獲型線位于截面激波曲線與激波曲線的曲率中心之間。而非軸對稱吻切技術能夠實現的原因是其不僅在橫向上對三維流場進行離散，在流向截面內同樣對流場進行離散，此外，沿流向曲率半徑變化的引入也為此類流場的求解提供了可能。

模型C的激波曲面在設計截面中的方程是二次曲線，其數值模擬結果與預設計激波形狀對比結果如圖10所示，與模型B類似，其結尾截面激波形狀所具有的曲率中心同樣已經超越了前緣捕獲型線。可以看到，逆向求解結果與數值模擬結果仍然具有較高的相似度。以此為基礎，本文在下文中將會詳細探討不同的二次錐面對乘波體升阻特性的影響。

圖11進一步提取了模型A的Y=0，Y=0.2，Y=0.4三個流向截面內的壓力分布信息，并與數值模擬結果進行對比分析。由圖11可知，運用逆向求解方法獲得的截面流場信息與數值模擬結果具有較高的相似度，各截面內的流場分布規律均與CFD結果表現出相同的趨勢。但在增壓比的預測上存在一定的誤差，其中對稱面內增壓比基本相同，而在Y=0.4截面內的增壓比誤差最大為8.4%。這主要是因為基于非軸對稱吻切技術的逆向求解方法實際上是將三維復雜流動簡化為一系列微吻切平面內的二維流動進行求解的過程，假設所有流動均在這些微吻切平面構成的流面內進行。在Y=0.4截面附近，激波曲率變化劇烈，流場中的橫向流動效果顯著，導致部分氣流并未沿微吻切平面流動，這在一定程度上將帶入一定的誤差。

由此可見，基于非軸對稱吻切技術的三維激波逆向求解方法能夠運用于三維流場的求解，且在激波形狀求解上具有較高的精度，激波吻合度較高，而在流場信息預測上，逆向求解獲得流場分布與CFD結果具有相同的規律，但在增壓比預測上存在一定誤差，誤差主要集中在遠離對稱面的三維效應較為明顯的部分。總體而言，本文提出的三維激波逆向求解方法能夠以較小的誤差完成復雜三維激波曲面的逆向求解。

4激波曲面對乘波體升阻特性影響

在上文模型C的研究基礎上，本文著重探討了不同二次錐面的激波形狀對乘波體升阻特性的影響。本文選取了4種不同的二次錐面，其頂點坐標均為（0，0，0），設計截面為X=5.1；設計截面內的準線方程均為二次曲線：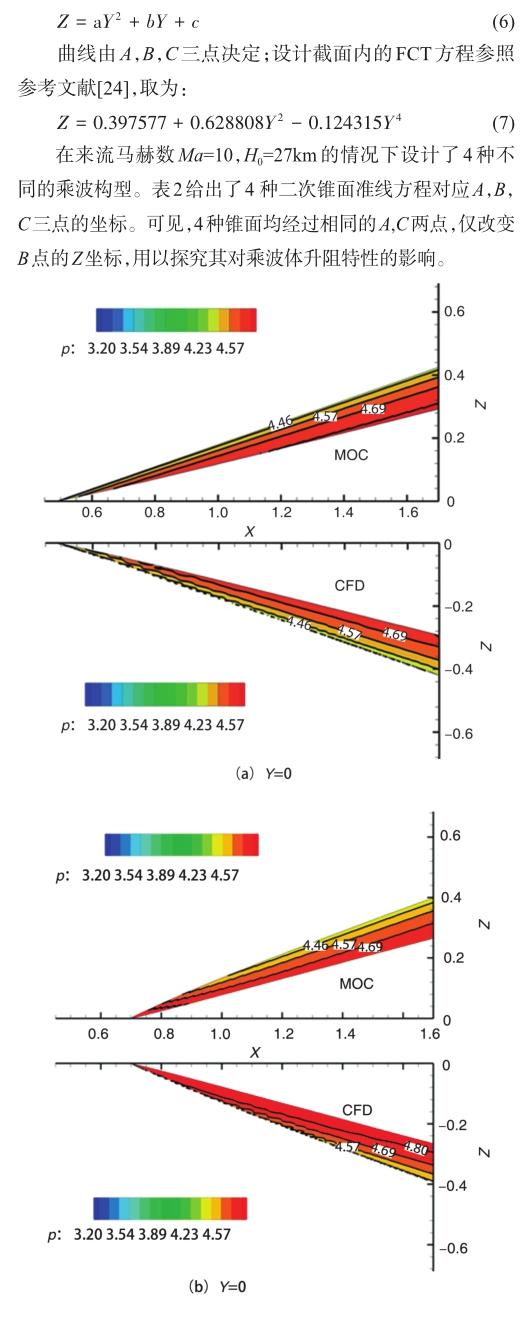

鑒于B的Z坐標的絕對值實際表示設計截面內激波曲線距離壓縮面的高度，故用H表示B的Z坐標的絕對值，根據H值由小到大分別將乘波構型命名為構型1～構型4。

圖12為4種乘波體在設計截面內的激波曲線及曲率中心分布圖。可以發現，隨著H的增大，激波曲線對應的曲率中心整體不斷下移。當H=2.0000時，已經有部分曲率中心位于FCT和ICC之間，即激波曲線與曲率中心位于前緣型線的同一側。此時現有的吻切乘波理論顯然并不適用，而這正是本文提出的基于非軸對稱吻切技術的三維激波逆向求解方法的優勢之一，其能夠求解更為復雜的激波曲面，拓寬了乘波理論的應用范圍。

4種乘波體的幾何模型如圖13所示。乘波體的下表面由本文所述求解方法逆向求解指定激波所得，上表面則直接將前緣型線延來流方向直接拉伸至設計截面所得。4種乘波體的寬度相同，均為W=3.0000，長度L基本相同，但隨著H的增大，L值也逐漸增加，其中構型4的值最大，為4.1344。乘波體高度方面，可以看到隨著H值的增大，乘波體的高度也越大，整體的迎風面積也逐漸增加。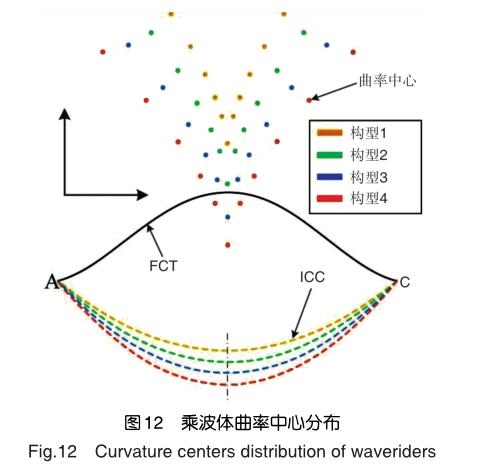

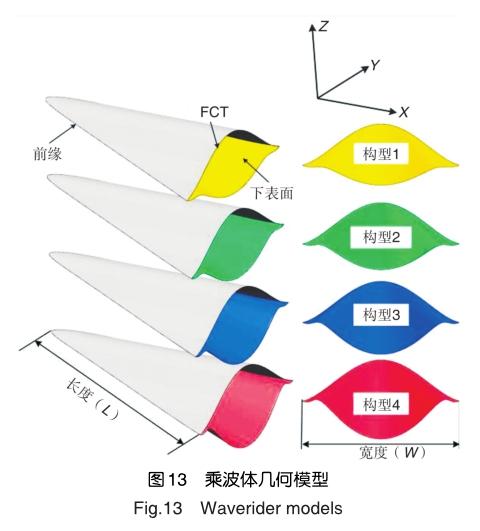
圖14給出了4種乘波體數值模擬結果與預定激波形狀對比圖。可以看到，在設計截面上4種乘波體所產生的激波與預設激波形狀具有較高的相似度。這說明本文提出的基于非軸對稱吻切技術的三維激波逆向求解方法在激波預測上具有較高的精確度，這與前文的分析是一致的。此逆向求解方法可用于探討不同高度的二次錐面激波對乘波體升阻特性的影響。

圖15為4種乘波體升力系數與阻力系數隨H值的變化曲線。其中，CL是升力系數，CD表示乘波體的阻力系數。左上坐標圖內σ表示升阻力系數用各自H=1.8時的值無量綱化后的結果，用于對比升阻力系數隨H值的變化速率。可以看到，升力系數與阻力系數均隨著H值的增大而增大，阻力系數與H值成線性增長關系，增長速率基本不變，表現為阻力系數成直線分布；而升力系數則成非線性增長關系，升力系數的增長速率隨著H值的增大而減緩，表現為升力系數成曲線分布。同時，從左上坐標圖中可以發現，阻力系數隨著H值的增長速率明顯大于升力系數。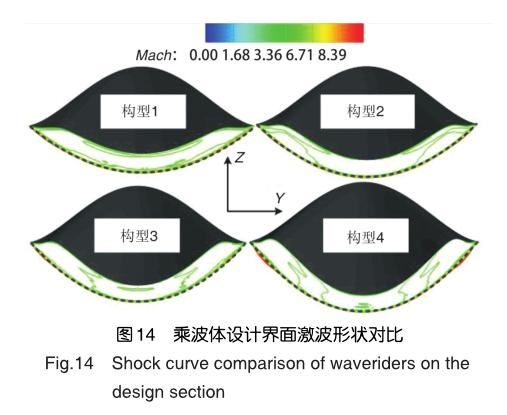

圖16給出了4種乘波體升阻比和迎風面積隨H值的變化曲線圖。圖中，L/D代表乘波體升阻比，Aw表示乘波體的迎風面積。參照圖16，乘波體的升阻比隨著H值的增加而減小，但并未成線性分布。這是因為4種乘波體的升力系數與阻力系數均隨著H值而增長，但阻力系數的增速更快，因此導致整體升阻比隨著H值而降低，且升阻比的降低速率逐漸減緩。同時可以發現，4種乘波體的迎風面積隨著H值成線性增長，這與前文的分析結果是一致的（見圖13）。

綜上所述，針對二次錐面激波，隨著H值的增加（即設計截面內激波曲線的高度增加），乘波體的迎風面積將成線性增加，導致其阻力特性同樣成線性增長。同時，隨著高度的增加，乘波體的升力系數也會增長，但升力系數的增長速率則逐漸減緩，且其增長速率低于阻力系數。最終導致其升阻比隨著高度的增加而降低，且降低速率逐漸減緩。可見，針對生成指定二次錐面激波的乘波構型，迎風面積的變化規律在其升阻特性中占主導地位，迎風面積越大，整體的升阻比越低。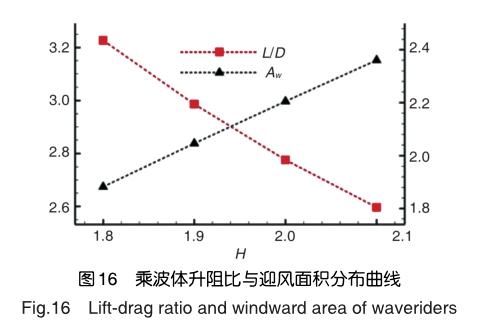

5結論

借鑒吻切乘波原理，本文提出了一種非軸對稱吻切技術，并在此基礎上，對傳統的二維逆向特征線法進行修正，發展了一種沿流向曲率中心可變的逆向特征線法，將其與非軸對稱吻切技術結合可用于逆向求解復雜的三維激波曲面。利用此逆向求解方法，本文設計了三種生成不同錐面激波的乘波體，并與CFD結果進行對比，用以驗證此逆向求解方法的正確性與可行性。同時，針對二次錐面激波，本文著重探討了設計截面內激波曲線高度對乘波體升阻特性的影響。研究結果表明：

（1）吻切乘波理論實際上是將三維流動在周向上離散成一系列等波強的二維軸對稱流動，在吻切面內，所有的激波角是恒定的。而非軸對稱吻切技術在此基礎上，進一步對流向同樣進行了離散，此時，每張微吻切面內的激波強度不再相同。因此，非軸對稱吻切技術本質上是將復雜的三維流動簡化為二維流動的過程，是對傳統吻切乘波理論的進一步拓展。

（2）本文提出的沿流向曲率中心可變的逆向特征線法在求解的過程中引入了曲率半徑這一變量，以此帶入激波曲面的三維效應，可用于求解具有三維效應的基準流場。因此，本文提出的基于非軸對稱吻切技術的三維激波逆向求解方法的實質是在微吻切平面內運用曲率中心可變的逆特征線法。

（3）對照模型A、模型B和模型C可以發現，本文提出的三維激波逆向求解方法在激波形狀求解上具有較高的精度，激波吻合度較高，而在流場信息預測上，逆向求解獲得流場分布與CFD結果具有相同的規律，但在增壓比預測上存在一定誤差，誤差主要集中在遠離對稱面的三維效應較為明顯的部分，其能夠以較小的誤差完成對復雜三維激波曲面的逆向求解。同時，由于本文提出的方法相比傳統的吻切乘波理論具有更高的自由度，其計算效率不可避免地有所降低。

（4）針對二次錐面激波，設計截面內激波曲線的高度越高，乘波體的升力系數與阻力系數均增大，且阻力系數的增長速度要快于升力系數，因而乘波體的升阻比呈下降趨勢。同時，可以看到，乘波體的迎風面積變化規律在升阻特性中占主導地位，迎風面積越大，整體的升阻比越低。

參考文獻

[1]Anderson B H. Design of supersonic inlets by a computer program incorporating the method of characteristics[R]. NASA TN D-4960，1969.

[2]Alexander K，Alexey K. Atmospheric cruise flight challenges for hypersonic vehicles under the ajax concept[J]. Journal of Propulsion and Power，2008，24（6）：128-131.

[3]劉濟民，沈伋，常斌，等.乘波體設計方法研究進展[J].航空科學技術， 2018， 29（4）：1-8. Liu Jimin， Shen Ji， Chang Bin， et al. Review on the design methodologyofwaverider[J].AeronauticalScience& Technology， 2018， 29（4）：1-8.（in Chinese）

[4]王驥飛，蔡晉生.形面漸變內收縮進氣道設計方法研究[J].航空科學技術， 2017， 28（1）： 30-35. Wang Jifei， Cai Jinsheng. Research on design of shape morphing inward turning inlet[J]. Aeronautical Science & Technology， 2017， 28（1）： 30-35.（in Chinese）

[5]尤延鋮，梁德旺，郭榮偉.高超聲速三維內收縮式進氣道/乘波前體一體化設計研究評述[J].力學進展，2009，39（5）：513-525. You Yancheng， Liang Dewang， Guo Rongwei. Overview of the integration of three-dimensional inward turning hypersonic inlet and waverider forebody [J]. Advances in Mechanics，2009，39（5）：513-525.（in Chinese）

[6]Nonweiler T R F. Aerodynamic problems of manned space vechile[J]. Journal of the Royal Aeronautical Society，1959，63（585）：34-40.

[7]Naruhisa T，Mark L. Wedge-cone waverider con-figuration for engine-airframe interaction[J]. Journal of Aircraft，1995，32：1142-1144.

[8]Naruhisa T，Mark L，Mary L. Waverider configu-ration development for the dual fuel vehicle[C]// Space Plane and Hypersonic Systems and Technology Conference，1996.

[9]Sobieczky H，Dougherty F C，Jones K D.Hypersonic waverider design from given shock waves[C]// Proceedings of the First International Hypersonic Waverider Symposium，1990.

[10]Rodi P E. Waverider vehicle optimization with volumetric constraints for sonic boom[C]// AIAA Aerospace Sciences Meeting，2018.

[11]耿永兵，劉宏，姚文秀，等.錐形流乘波體優化設計研究[J].航空學報， 2006， 27（1）：23-28. Geng Yongbing， Liu Hong， Yao Wenxiu， et al. Viscous optimized design of waverider derived from cone flow [J]. Acta Aeronautica etAstronautica Sinica， 2006， 27（1）：23-28.（in Chinese）

[12]湯波，高云峰，李俊峰，等.基于CFD計算和遺傳算法的乘波體優化[J].動力學與控制學報， 2008， 6（3）：270-274. Tang Bo， Gao Yunfeng， Li Junfeng， et al. Optimization of waverider configurations by CFD calculation and genetic algorithm[J]. Journal of Dynamics and Control， 2008， 6（3）：270-274.（in Chinese）

[13]You Y，Zhu C，Guo J. Dual waverider concept for the integration of hypersonic inward-turning inlet and airframe forebody[C]//16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference，2009.

[14]Li Y，You Y，Integration methodology for waverider-derived hypersonicinletandvehicleforebody[C]//19thAIAA International Space Planes and Hypersonic Systems and Technologies Conference，2014.

[15]賀旭照，秦思，周正，等.一種乘波前體進氣道的一體化設計及性能分析[J].航空動力學報， 2013，28（6）： 1270-1276. He Xuzhao， Qin Si， Zhou Zheng， et al. Integrated design and performance analysis of waverider forebody and inlet[J]. Journal ofAerospace Power， 2013，28（6）： 1270-1276.（in Chinese）

[16]范曉檣，李樺，易仕和，等.側壓式進氣道與飛行器機體氣動一體化設計及試驗[J].推進技術， 2004， 25（6）： 499-502. Fan Xiaoqiang， Li Hua， Yi Shihe， et al. Experiment of aerodynamic performance for hypersonicvehicle integrated with sidewall compression inlet[J]. Journal of Propulsion Technology， 2004， 25（6）： 499-502.（in Chinese）

[17]易軍，肖洪，商旭升.兩種高超聲速一體化構型的氣動性能對比分析[J].航空工程進展，2011，2（3）： 305-311. YiJun，XiaoHong，ShangXusheng.Aerodynamic performanceresearchoftwointegratedhypersonic configurations[J]. Advances in Aeronautical Science and Engineering，2011，2（3）： 305-311.（in Chinese）

[18]賀旭照，倪鴻禮.密切曲面錐乘波體——設計方法與性能分析[J].力學學報， 2011， 43（6）：1077-1082. He Xuzhao， Ni Hongli. Osculating curved cone （OCC） waverider： design methods and performance analysis[J]. Chinese Journal of Theoretical and Applied Mechanics， 2011， 43（6）：1077-1082.（in Chinese）

[19]李怡慶，韓偉強，尤延鋮，等.壓力分布可控的高超聲速進氣道/前體一體化乘波設計[J].航空學報， 2016， 37（9）：2711-2720. Li Yiqing， Han Weiqiang， You Yancheng， et al. Integration waverider design of hypersonic inlet and forebody with preassigned pressure distribution[J]. Acta Aeronautica et Astronautica Sinica， 2016， 37（9）：2711-2720.（in Chinese）

[20]鐘啟濤，張堃元，龐麗娜.出口馬赫數分布可控的二維高超進氣道雙重反設計[J].推進技術， 2015， 36（7）：982-988. Zhong Qitao， Zhang Kunyuan， Pang Lina. Double inverse design of 2D hypersonic inlet with controllable exit Mach number distribution[J]. Journal of Propulsion Technology， 2015， 36（7）：982-988.（in Chinese）

[21]藍慶生，趙玉新，趙一龍.降維的三維特征線方法與應用[C]//中國航天空天動力聯合會議，2017. Lan Qingsheng， Zhao Yuxin， Zhao Yilong. Method and application of 3D characteristic line of dimension reduction[C]// Joint Conference ofAerospace Propulsion， 2017.（in Chinese）

[22]藍慶生，趙玉新，趙一龍，等.三維超聲速流動的壓力反問題[J].空氣動力學學報， 2017， 35（3）：429-435. Lan Qingsheng， Zhao Yuxin， Zhao Yilong， et al. Pressure inverse problem of three-dimensional supersonic flow[J]. Acta Aerodynamica Sinica， 2017， 35（3）：429-435.（in Chinese）

[23]Center K B，Sobieczky H，Dougherty F C. Interactive design of hypersonic waverider geometries[C]// AIAA 22nd Fluid Dynamics，Plasma Dynamics and Lasers Conference，1991.

[24]Ding F，Shen C B，Liu J，et al. Influence of surface pressure distribution of basic flow field on shape and performance of waverider[J].ActaAstronautica，2015，108：62-78.

（責任編輯王昕）

作者簡介

張濤（1997-）男，碩士研究生。主要研究方向：高超聲速空氣動力學、計算流體力學。

Tel：15256555449E-mail：1457745879@qq.com

鄭曉剛（1994-）男，博士研究生。主要研究方向：高超聲速推進技術研究、內外流流體力學。

Tel：18959216039E-mail：xiaogangzheng@stu.xmu.edu.cn湯祎麒（1998-）男，碩士研究生。主要研究方向：高超聲速氣體動力學、彎曲激波理論、計算流體力學。

Tel：18850013602E-mail：tangyiqi2019@163.com

李怡慶（1989-）男，博士，助理教授。主要研究方向：高超聲速推進技術研究、內外流流體力學、計算流體力學。

Tel：13306019011E-mail：yiqingli@nchu.edu.cn

尤延鋮（1981-）男，博士，教授。主要研究方向：高超聲速空氣動力學、內流流體力學、高超聲速進氣道設計、復雜湍流數值模擬（LES/DES）和CFD計算數值方法研究等。

Tel：18060979961E-mail：yancheng.you@xmu.edu.cn

Inverse Waverider Design for 3D Shock Wave Based on Non-axisymmetric Osculating Cones Method

Zhang Tao1，Zheng Xiaogang1，Tang Yiqi1，Li Yiqing2，You Yancheng1，*

1. Xiamen University，Xiamen 361102，China

2. Nanchang Hangkong University，Nanchang 330063，China

Abstract： Based on the principal of traditional osculating cones method， a new non-axisymmetric osculating cones method was proposed. On this basis， the traditional 2D MOC was improved， which can be used to solve the 3D complicate shock wave. By specifying the appearance of three-dimensional shock wave in advance， the local micro osculating plane corresponding to the discrete shock points can be obtained according to the direction of the air flow and the local curvature direction of the shock surface. The improved two-dimensional inverse MOC is used to solve the flow field in each micro osculating plane， while the intersection line between the micro osculating plane and the shock surface is defined as the main input. Subsequently， the compression surface， designed to generate specified 3D shock wave， are formed with all the compression lines gained from each micro osculating plane. The results show that the inverse technology for solving 3D shock wave via non-axisymmetric osculating cones method shows high agreement in the shape of shock wave， and the flow field information obtained by this inverse technique is quite similar to the numerical simulation results. However， there is still a certain deviation in the prediction of the pressure ratio， while the maximum deviation is about 8.4%. In addition， for the specific quadric conical shock wave， the higher the shock curve is in the design section， the lower lift-drag of waveriders is.

Key Words： non-axisymmetric osculating cones method； method of characteristic （MOC）；waverider； lift-drag ratio； inverse design