基于Adaptive Lasso的股票指數跟蹤問題研究

侯紅衛，謝 儀

(1.太原理工大學 數學學院，太原 030024；2.中國人民銀行 烏魯木齊中心支行，烏魯木齊 830000)

投資者進行股票投資最直接的動機是獲得理想回報，故而投資決策的目標是收益的最大化。然而，收益和風險是正相關的，股市的波動一方面帶來了投資收益，另一方面也帶來了很高的投資風險，二者互相依存。我國的證券市場近年來一直處于高速發展過程中，但其系統性風險依然很大，投資者一直在尋求能夠獲得穩定收益的方法，尤其是當指數化基金、股指期貨、ETF等衍生產品的不斷推出，指數化投資被越來越多的人所關注。指數跟蹤作為指數化投資的具體管理形式，可以有效地指導股指期現套利、指數投資產品的設計等[1]。

股票指數跟蹤，是指用一定方法構建投資組合以復制和跟蹤某一市場指數為目標，來獲得與之相同的市場平均收益。由于其分散化、被動式管理等優點，不但可以充分消除系統風險，還可以大大降低交易成本。因此，如何構建一個合理的股票投資組合并使其擁有較小的跟蹤誤差便成了一個重要問題。股票指數跟蹤技術主要需要解決兩方面問題，一方面需要選取組合中的成分股，一方面需要確定成分股在組合中的權重。楊國梁等[2]將數學上處理高維變量選擇問題的Lasso方法運用于股票投資組合構建中，取得了現有文獻最好的跟蹤效果。然而，Lasso方法本身確實存在一些缺陷。首先，若股票收益率存在嚴重共線性時，Lasso的選擇效果會被削弱，其次是Lasso方法并不具有Oracle性質，而具備Oracle性質可以使得系數向量更接近真實值，且估計具有漸進相合性。ZOU[3]提出了Adaptive Lasso，該方法不但沿襲了Lasso方法的諸多優點，而且能有效減少模型參數估計的有偏性，具有Oracle性質。因此，將Adaptive Lasso方法運用于跟蹤指數的股票選擇中是一種很好的嘗試。

1 指數跟蹤方法

1.1 指數跟蹤基本方法

現有的指數跟蹤方法，按照原理不同，主要可以分完全復制法與不完全復制法兩類。完全復制法是指購買標的指數中所有證券，并且各成分證券的權重完全復制標的指數的權重。其優點是能獲得與標的指數相同的收益，擁有最小的跟蹤誤差，缺點是當指數構成變化時必須及時調整，從而產生非常高的交易成本。不完全復制法是指購買標的指數中的部分證券，使得收益率偏差在可控范圍內，行業抽樣配置法、市值占比法等都屬于不完全復制法。由于不完全復制法可達到用較少證券獲得較好跟蹤效果的優勢，因此國內外學者做了很多關于不完全復制法的研究。ROLL[4]基于Markowitz均值-方差模型，通過最小化指數跟蹤誤差與投資組合來確定成分證券的權重；ZORIN et al[5]將神經網絡技術運用于指數跟蹤方法也得到不錯的結果，Corielli與Marcellino基于動態因子模型研究也解決了構建投資組合的問題。

1.2 Adaptive Lasso方法

1.2.1Adaptive Lasso簡介

Adaptive Lasso的形式為：

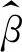
1.2.2Adaptive Lasso的算法實現

EFRON et al[6]提出的最小角回歸算法(least angle regression，LARS)有效解決了此模型的求解問題；FAN et al[7]提出的循環坐標下降算法(cyclic coordinate descent，CCD)利用模型稀疏性的假定，算法簡單運行快速；他還提出LQA方法對目標函數采用局部二次近似，然后采用Newton-Raphson迭代算法也可以十分便捷的得到計算結果。本文實證研究部分主要利用R軟件的lqa package，其采用的就是LQA算法。LQA算法的數學思想描述如下：

記Adaptive Lasso的懲罰函數為pλ(|βj|)，pλ(|βj|)=λwj|βj|.

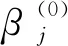
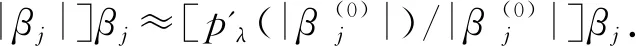
那么Adaptive Lasso懲罰函數的二階Taylor近似展開函數為：

利用Newton-Raphson迭代算法，給可以出一個不含懲罰項的似然估計初始值β(0)，Adaptive Lasso就轉換成了下面的形式的迭代求解問題：

當‖β(k)-β(k-1)‖<η時，算法終止，其中η可以取一個很小的正值。

2 Adaptive Lasso方法選擇股票及實證分析

Y=Xβ+ε.

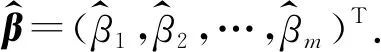
2.1 樣本數據的選取

本文選擇的指數跟蹤對象為滬深300指數，選取了2015年8月3日—2017年10月28日，538個交易日的滬深300指數及各成分股的日收益率數據，其中2015年8月3日—2017年4月28日，共422個交易日為樣本內區間，2017年5月5日—2017年10月28日，共116個交易日為樣本外區間，用以檢測跟蹤效果。數據來源為網易財經。

2.2 Adaptive Lasso變量選擇結果分析

基于Adaptive Lasso的基本思想，在R軟件中運用LQA方法編程，便可同時實現股票的選擇與權重的估計。圖1-圖3為100只股票，50只股票，30只股票的篩選過程。

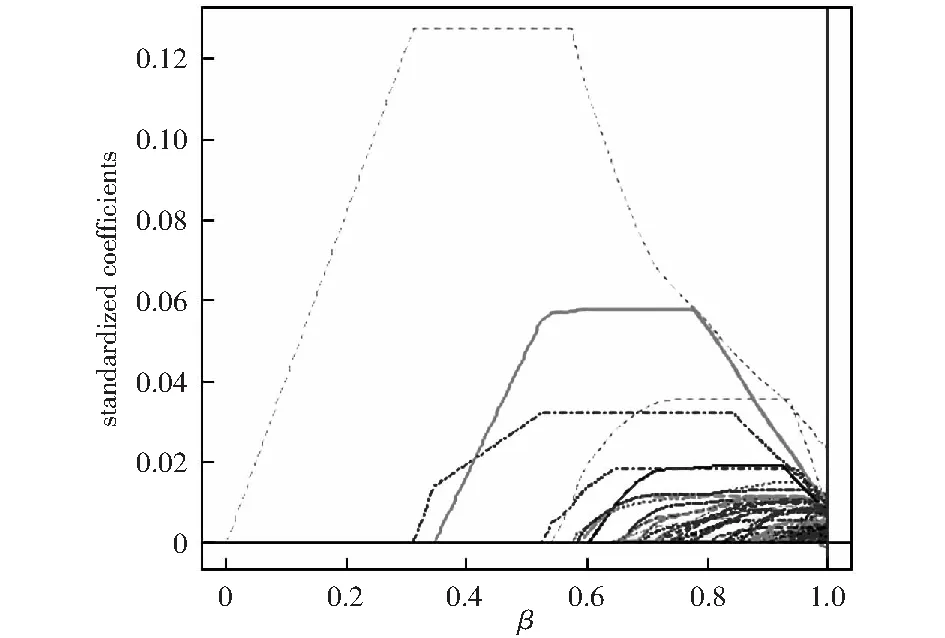
圖1 100只股票的篩選過程

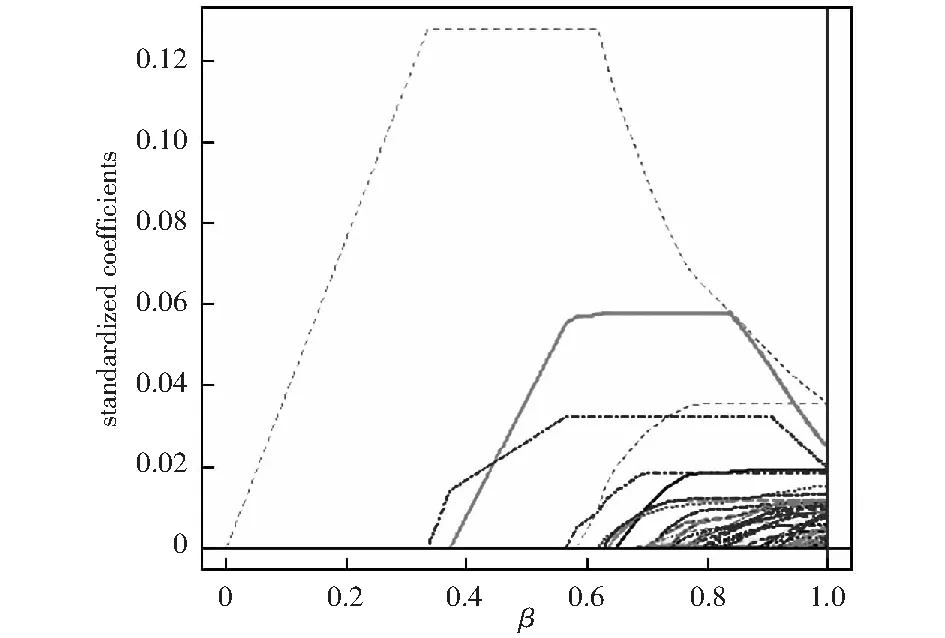
圖2 50只股票的篩選過程

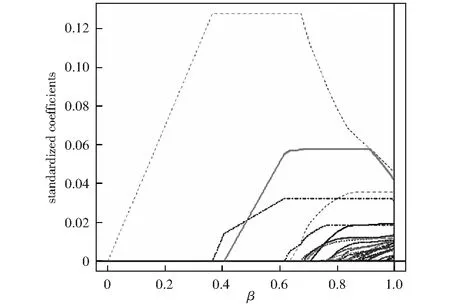
圖3 30只股票的篩選過程

由圖1-圖3可以看出，Adaptive Lasso可以得到稀疏模型，隨著參數的增大，一部分系數被壓縮為0，即沒有入選的股票所對應的系數β=0，入選的股票所對應的系數β>0，表1-表3為篩選出的股票名稱及其權重系數。

2.3跟蹤結果分析

為了對股票組合的跟蹤效果進行評估，本文從相關系數、跟蹤誤差、最大正向誤差和最大負向誤差這4個方面驗證分析，并比較了樣本內區間與樣本外區間的跟蹤效果，如表4、表5所示。

表1 Adaptive Lasso選出的30只股票及權重系數

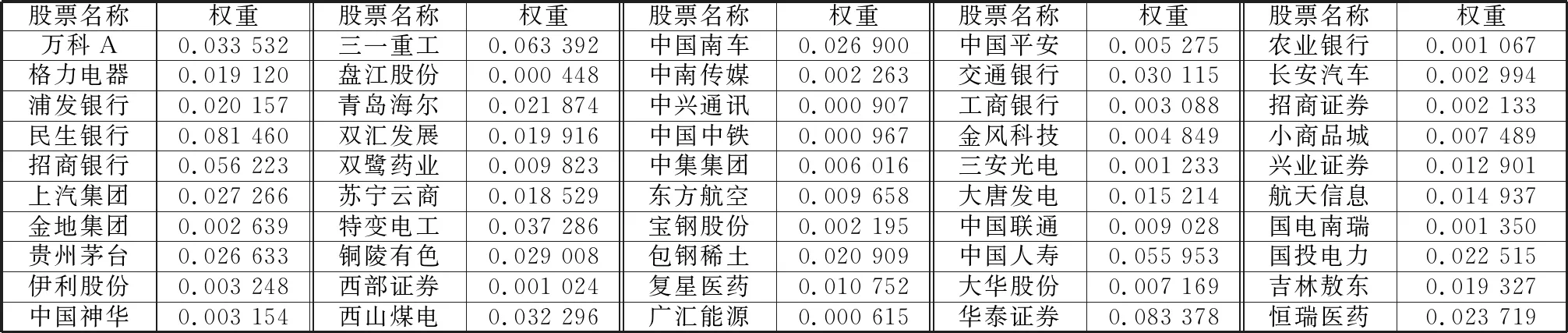
表2 Adaptive Lasso選出的50只股票及權重系數

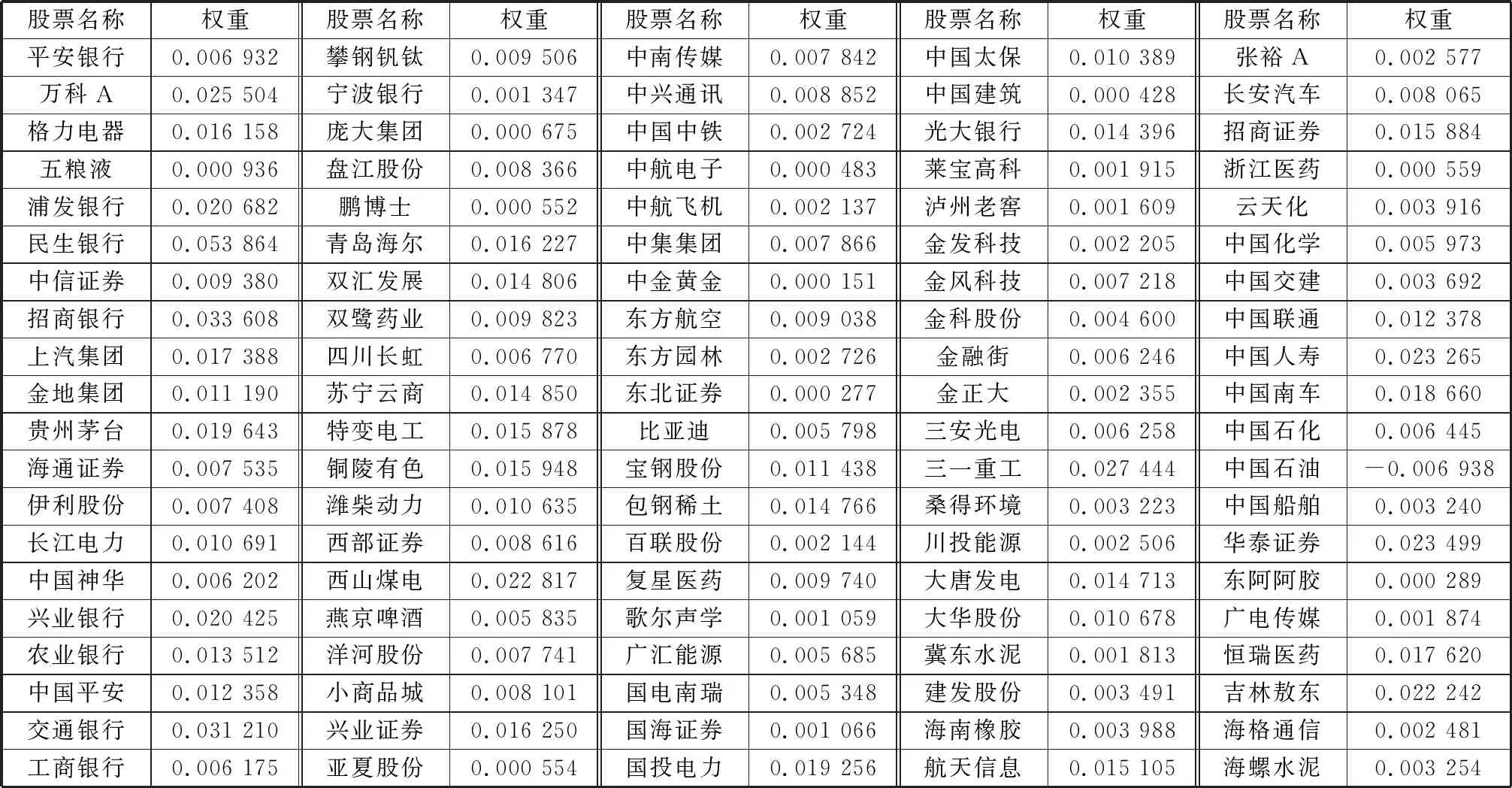
表3 Adptive Lasso選出的100只股票及權重系數

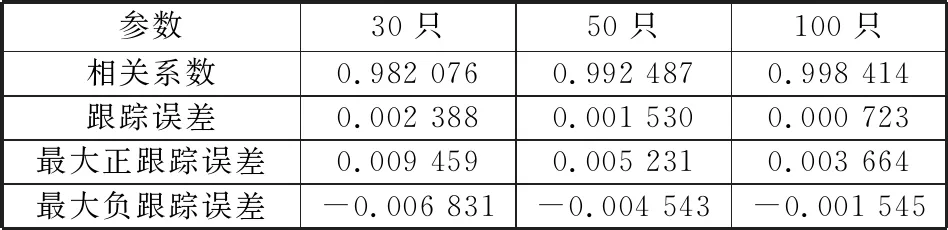
表4 樣本內指數跟蹤效果

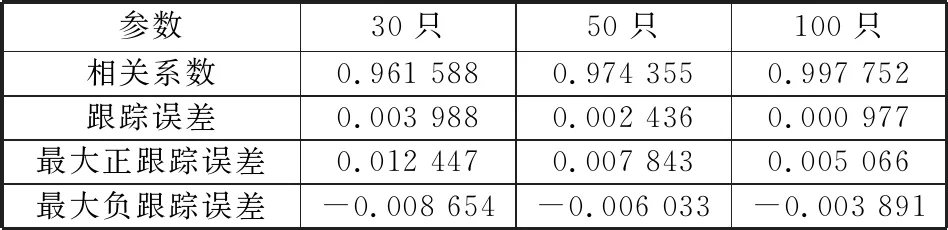
表5 樣本外指數跟蹤效果

結果顯示，采用Adaptive Lasso方法構建股票組合，無論是30只、50只還是100只，都取得了非常好的跟蹤效果。由樣本內與樣本外跟蹤結果可看出：1) 相關系數均保持在0.96以上，說明成分股與滬深300指數相關程度很高，即指數跟蹤的風險很小。2) 跟蹤誤差均可以控制在0.4%之內，指數擬合復制效果很好。3) 隨著成分股的數量增多，相關系數增大，跟蹤誤差及最大正向誤差和最大負向誤差減小，說明成分股越多跟蹤效果越好，這是顯然的。4) 從整體看來，樣本內指數跟蹤效果要優于樣本外指數跟蹤效果，雖然樣本外各指標數據都有一定的下降，但是幅度并不大，預測能力也是較強的。

3 結論

在瞬息萬變的股票市場中，尋求一種性能良好的跟蹤方法對目標指數進行有效跟蹤，以此構建最佳股票組合，對于所有投資者而言具有十分重要的意義。本文將處理高維數據變量選擇的Adaptive Lasso方法，運用于指數跟蹤，同時完成了股票投資組合中成分股的選取與權重系數的估計問題。在實證分析部分中，利用Adaptive Lasso方法選擇股票對滬深300指數進行跟蹤，并從跟蹤誤差、相關系數等方面來衡量。通過比較可以看出，Adaptive Lasso方法可以達到比較理想的跟蹤效果，具有一定的實用性，這也為金融市場的股票組合投資選擇提供了一種新的方法。投資者進行股票投資最直接的動機是獲得理想回報，故而投資決策的目標是收益的最大化。然而，收益和風險是正相關的，股市的波動一方面帶來了投資收益，另一方面也帶來了很高的投資風險，二者互相依存。我國的證券市場近年來一直處于高速發展過程中，但其系統性風險依然很大，投資者一直在尋求能夠獲得穩定收益的方法，尤其是當指數化基金、股指期貨、ETF等衍生產品的不斷推出，指數化投資被越來越多的人所關注。指數跟蹤作為指數化投資的具體管理形式，可以有效的指導股指期現套利、指數投資產品的設計等。