考慮剪力滯效應和附加軸力的箱梁自振分析

李夢瑤

(昆明理工大學 建筑工程學院，云南 昆明 650500)

箱梁因自重輕、施工方便等優點被廣泛應用于橋梁建設中。因為箱梁截面非實心，所以箱梁截面的應力分布較復雜，剪力滯效應尤為突出。當箱梁承受豎向荷載產生豎向撓曲變形時，上、下翼緣板產生剪切變形，而腹板在上、下翼緣板之間傳遞剪力流過程中，由于應力集中，導致翼緣板縱向位移，沿橋寬方向產生不均勻的變化，這種現象叫剪力滯效應。所有箱梁結構的動力分析都要求對其剪力滯效應進行分析，因此，許多學者對此進行了大量的研究。吳有俊等[1?2]人基于實際變形下中性軸和形心軸的重合，根據能量變分原理進行推導，得到了考慮剪力滯效應的簡支梁強迫振動微分方程及其邊界條件。藺鵬臻等[3?5]人根據簡支梁的縱向靜力平衡條件進行推導，得出了附加軸力的表達式，并研究了其對剪力滯效應的影響。潘旦光[6]等人采用模態攝動法求解出簡支薄壁箱梁自由振動解析解，根據簡支梁振動模態提出了模態剪力滯系數的概念，并建立了剪力滯效應與自振頻率之間的關系。蔡恒[7]等人根據能量變分原理推導出曲線梁橋的自由振動微分方程，并假設位移場函數為正弦函數，對微分方程近似求解。劉建新[8]等人利用能量變分法推導出簡支梁強迫振動方程，建立了微分方程解的差分格式，討論了差分格式的準確性。甘亞南[9?11]等人根據能量變分法推導出簡支曲線梁和連續梁的彎曲振動方程和邊界條件，利用Matlab 軟件編程求解得到了固有頻率。目前，針對橋梁靜荷載作用下的剪力滯效應已經獲得許多研究成果[12?14]，而且多數橋梁的動力響應中多數考慮了地震作用[15]，但是同時考慮動剪力滯效應和縱向靜力平衡的研究鮮見。因此，作者基于能量變分原理，擬在縱向位移函數中增加全截面均勻縱向位移，推導出同時考慮剪力滯效應和縱向靜力平衡的簡支箱梁自由振動微分方程，并根據假設模態法對微分方程分離參數，利用Matlab 編程求解自振頻率，并與初等梁理論、ANSYS 有限元建模和考慮剪力滯效應的計算結果進行對比分析。

1 模型建立

1.1 基本假定

為了便于分析，忽略部分影響較小的因素，并做出假設：①考慮剪力滯效應時，截面中性軸仍然通過截面形心；②不計阻尼的影響，所有材料均處于線彈性狀態；③翼板縱向位移沿寬度方向按3 次拋物線分布[16]；④箱梁截面處于對稱彎曲狀態。

分析的箱梁截面尺寸如圖1 所示。在圖1 中，b1,b2,b3,b4分別為頂板寬度、懸臂板寬度、底板寬度、腹板高度；h1,h2,h3,h4分別為頂板厚度、懸臂板厚度、底板厚度、腹板厚度；坐標軸采用直角坐標軸，x軸為縱向，y 軸為橫向，z 軸為豎向。

1.2 振動微分方程及邊界條件

當i=1 時，表示頂板；當i=2 時，表示懸臂板；當i=3 時，表示底板；當i=4 時，表示腹板。箱梁的縱向位移函數為：

式中： Ui( x , y , z , t )為箱梁的縱向位移函數；Zi為各個板到形心的距離；w 為豎向撓度；為剪力滯效應引起的附加縱向位移； fi( y , z )為u(x)的分布函數。

圖1 截面尺寸Fig.1 Section size chart

考慮到簡支梁截面縱向靜力平衡，由于中性軸與形心軸偏離產生軸力，因此，用附加軸力來進行平衡，將附加軸力引起的縱向位移均勻分布在全截面上。附加軸力的作用下，箱梁的縱向位移函數為：

其中，

式中：ξ 為由軸力引起的縱向位移；y 為箱梁截面待求點的y 坐標。

正應變：

切應變：

根據材料力學中軸力的定義，可得：

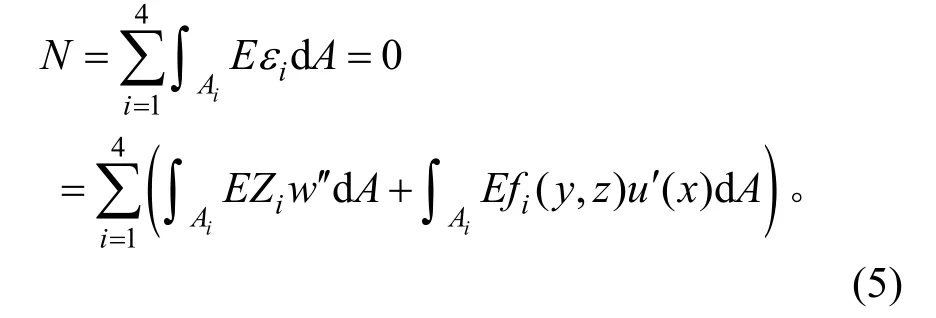
式中：E 為彈性模量；A 為箱梁截面的面積。

由于截面中性軸通過截面形心，則截面對形心軸 的 靜 矩 為 0，可 得明 顯因此，附加軸力為：

則：

其中，式(7)對y 積分，可得：

式中：A1為頂板的橫截面積；A2為懸臂板的橫截面積；A3為底板的橫截面積。

頂板應變為：

同理可得，懸臂板應變能為：

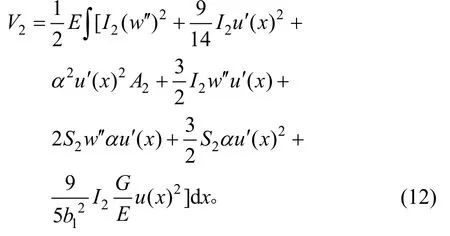
底板應變能為：

腹板應變能：

箱梁的動能(僅考慮豎向振動)：

式中：m(x,t)為單位長度的質量。

外荷載所做的功為：

式中：P 為外荷載。

箱梁應變能：

根據哈密頓原理，可知：

式中：δ 為變分符號。

邊界條件為：

1.3 振動方程求解

由方程(19)可得：

將(22)，(23)代入(20)，

因研究箱梁的自振分析，則P=0。

令：

式中：ω0為振幅；N 為振型階數；l 為跨長；ωN為固有角頻率；t 為時間；θ 為初相角。

要使式(25)恒等于0，只需令

2 算例及結果

某混凝土簡支箱形截面梁如圖1 所示，其尺寸參數及材料參數為：泊松比為 0.3，彈性模量E=3.5×1010Pa，b1=3 m，b2=3 m，b3=3 m，b4=3 m，h1=0.3 m，h2=0.3 m，h3=0.3 m，h4=0.3 m，密度為2 500 kg/m3。采用ANSYS 有限元軟件和Matlab 程序，對不同跨寬比的簡支箱梁自振頻率進行計算，并與初等梁理論和考慮剪力滯效應變分法的計算結果進行比較，見表1。

由表1 可知，考慮剪滯和軸力的計算結果，與初等梁理論和考慮剪力滯效應的相比，更接近有限元的。跨寬比為3.33 時，振型階數從一階到四階，采用推算方法，計算出自振頻率分別為20.170,72.106,145.115,236.248 Hz，均小于初等梁理論和考慮剪力滯效應的結果。表明：考慮剪力滯效應和附加軸力修正的解析解，能夠與ANSYS 有限元解吻合。ANSYS 有限元建模過程中，采用BEAM188單元和自底向上的建模方式，約束條件為簡支約束，進行模態分析。

根據不同跨寬比的箱梁結果見表2。由表2 可知，附加軸力對自振頻率計算精度的影響，跨寬比的增大，附加軸力對自振頻率的影響略微變大，但穩定在10%左右。當假設簡支梁變形時，中性軸與形心軸位置一致，而實際變形過程中，軸力會對結構的振動產生影響[17]，中性軸與形心軸的位置會產生一定偏移，從而產生了附加軸力。附加軸力會使簡支箱梁的相對剛度減小，從而導致結構的自振頻率降低，進而使得簡支箱梁的自振頻率降低。附加軸力對自振頻率計算精度的影響已經超過了工程精度的容許值，故求解箱梁自振頻率過程中，對附加軸力的考慮是必要的。

表1 各計算方法的自振頻率(單位：Hz)Table 1 Frequency comparison of natural vibration (unit: Hz)

通過對不同振型階數考慮剪力滯效應、初等梁理論、推算方法與有限元建模所得的自振頻率進行比值分析。令有限元結果為1，各計算結果如圖2所示。從圖2 可以看出，當振型階數一定時，這3種方法隨著跨寬比的增加，與有限元模擬結果逐漸接近。當跨寬比為1.67 時，本計算方法與其他兩種方法相比，最為接近有限元的結果。當跨寬比為5時，3 種方法與有限元結果均相近。當振型階數從一階到四階時，3 種方法與有限元的計算結果的比值均大，但推算計算方法所得結果相比于其他2 種方法與有限元結果最為接近。由于簡支箱梁的剪力滯效應程度受到跨寬比的影響，當跨寬比越小，剪力滯效應越嚴重，減小了結構的相對剛度，因此，對簡支箱梁的自振頻率降低程度越大。

表2 附加軸力的影響Table 2 Effect of the additional axial force

圖2 自振頻率的比值Fig.2 Ratio of natural frequency

3 結論

通過對簡支箱梁縱向靜力平衡狀態下的剪力滯效應分析，得出的結論為：

1) 推算的結果與ANSYS 有限元的較為接近，精度能夠滿足工程需求，具有一定實用性。

2) 考慮剪力滯效應的自振頻率，相比于初等梁理論偏小，是因為剪力滯效應減小了箱梁的相對剛度，使得簡支箱梁的自振頻率降低，且結構隨著跨寬比的減小，剪力滯效應越明顯。

3) 附加軸力會造成箱梁相對剛度的減小和自振頻率的降低。