滑翔飛行器多目標彈道優化的進化-配點混合求解策略*

豐志偉，江增榮，張青斌，葛健全，黃 浩

(1. 國防科技大學 空天科學學院， 湖南 長沙 410073； 2.中國人民解放軍96901部隊， 北京 100094)

高超聲速滑翔飛行器(Hypersonic Glider Vehicle，HGV)具有高速度、高機動、長航程等諸多優勢，成為未來飛行器發展的一個重要方向，具有廣闊的軍事應用前景[1]。

彈道優化技術是高超聲速滑翔飛行器的關鍵技術之一。隨著研究的不斷深入，在進行高超聲速滑翔飛行器彈道設計之中，不僅要考慮飛行器在飛行過程中受到的氣動熱、動壓、過載、控制量、終端約束等復雜約束條件的限制，還需要考慮面向具體作戰任務的要求，如航路點、禁飛區等。面對諸多性能指標，設計者往往不能追求單個指標最優，而是需要同時考慮多個相關的性能指標，利用多目標優化方法進行求解，獲得Pareto最優解，從而對各個指標進行權衡和折中[2]。

對于高超聲速滑翔飛行器的多目標彈道優化問題而言，工程上常用的方法是利用偏好(權重)信息，將多個目標聚合為單個目標，并采用成熟的單目標優化算法進行求解。主要優化方法包括加權法、理想點法、物理規劃法、主要目標法等[3]。雍恩米等[4]應用物理規劃法設計再入飛行最優攻角；謝愈等[2]將物理規劃法應用于高超聲速飛行器多目標復雜約束滑翔彈道優化設計，結合高斯偽譜法獲得了滿足設計者偏好的滿意解。上述基于偏好的方法每次只能優化得到一個解，無法得到整個Pareto前沿(Pareto Front, PF)。為了獲得多個Pareto最優解(Pareto Set, PS)，通常需要采用多目標優化方法來進行設計。主要優化方法包括各種多目標進化算法、多目標粒子群算法等[5]。例如，陳剛、王明光等[6-7]將多目標遺傳算法NSGA-II成功應用于可重復使用運載火箭最優再入彈道優化設計；豐志偉等[8]應用分解多目標進化算法(Multiobjective Optimization Evolutionary Algorithm based on Decomposition, MOEA/D)求解火星再入飛行器一體化多目標優化設計問題。

滑翔飛行器彈道優化問題是一個帶有復雜約束的最優控制問題，本文綜合考慮計算效率和精度，提出一種結合進化算法和配點法的混合、分層多目標優化策略。為了獲得具有較高精度的全局最優解，將多目標彈道優化問題的求解分為兩步：①使用較少節點對彈道優化問題進行離散化處理，采用MOEA/D進行多目標優化計算，獲得Pareto前沿和全局最優解集；②以多目標最優解作為基于二代小波節點自適應配點法[9]的初始解進行精細優化，獲得較高精度的彈道。特別是，在MOEA/D和自適應配點法中采用了橢球聚合法[10]將多個目標函數聚合為單個目標函數。

1 滑翔飛行器多目標彈道優化模型

1.1 再入動力學方程

以地心距r、經度λ和緯度φ描述飛行器位置，以速度大小V、速度傾角θ和速度偏角σ描述飛行器速度，建立的滑翔飛行器三自由度運動方程[11]可表示為

(1)

其中：X為阻力，Y為升力，L為側向力，m為飛行器質量，g為引力加速度；速度傾角θ為速度矢量與當地水平面的夾角，速度偏角σ為速度矢量在當地水平面投影與正北方向的夾角；ωe為地球自轉角速度，ν為側傾角。由于滑翔飛行器為面對稱升力體，通常采用傾斜轉彎(Bank To Turn, BTT)技術，在上述運動方程中假設側滑角為零。

1.2 約束條件分析

滑翔飛行器多目標彈道設計約束條件[12]包括：熱流、動壓、過載、平衡滑翔、禁飛區、航路點等過程約束；彈道末端需滿足的終端狀態約束；對攻角、側傾角的控制量約束。

1)氣動熱、過載和動壓約束：為了保證飛行器結構安全，對沿彈道飛行的熱流密度、動壓、過載等進行限制。

駐點熱流密度約束為

(2)

過載約束為

(3)

式中，α為攻角。

動壓約束為

(4)

2)擬平衡滑翔約束：為保證彈道平穩，沿彈道飛行器可獲得的最大升力須能夠平衡其他力，即

(5)

3)禁飛區約束：禁飛區指飛行需要規避的區域，包括躲避雷達探測等。為便于計算，假設禁飛區為無限高圓柱，彈道點與禁飛區中心在地面投影的最短距離滿足如下約束

|R0·arccos[sinφsinφnfz+

cosφcosφnfzcos(λ-λnfz)]|>Rnfz

(6)

其中，λnfz和φnfz分別表示禁飛區中心經緯度，Rnfz表示禁飛區半徑。

4)控制量約束：由于受執行機構能力限制，攻角、側傾角等物理量的幅值存在約束邊界

(7)

5)終端約束：本文主要開展最大射程優化，不約束滑翔段終點的位置和速度。

1.3 性能指標

按照飛行任務的不同，可選擇不同的性能指標。常用的優化目標有終端射程最大、飛行時間最短、總加熱量最小等。如取終端射程最大為優化指標，則

J=min[-L(tf)]

(8)

當選擇總加熱量最小作為性能指標時，則

(9)

2 多目標優化問題的混合求解策略

多目標彈道優化問題的核心是獲得一組較為精確的Pareto全局最優解集。為此，本文提出結合分解多目標進化算法和配點法的混合求解策略。為了保證兩種多目標優化方法求解問題的一致性，均采用橢球聚合法[10]將多目標優化問題轉化為單目標優化問題。

2.1 混合求解策略

混合求解策略優化流程如圖1所示。具體計算過程如下：

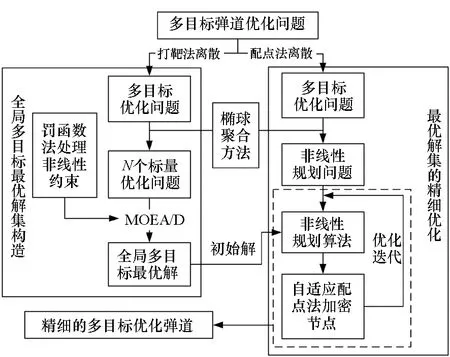
圖1 混合求解策略流程圖Fig.1 Flow chart of hybrid optimization strategy

1)定義多目標彈道優化問題：定義狀態方程，確定控制量、優化目標和約束條件。

2)彈道優化問題的離散：分別采用打靶法(僅離散控制量)和配點法(同時離散控制量和狀態量)將彈道優化問題轉化為多目標優化問題。

3)全局多目標最優解集的構造：采用MOEA/D對控制量離散方法得到的多目標優化問題進行優化計算。設置合理的優化參數，如種群規模和迭代步數，獲得全局多目標最優解。

4)最優解集的精細優化：采用非線性規劃算法對配點法得到的優化問題進行求解，以MOEA/D得到的控制量和狀態量作為初始解進行優化迭代，采用自適應配點法進行網格自適應加密以提高求解精度。

需要說明的是：①為了求得全局最優解，首先采用進化算法求解，考慮計算效率問題，采用打靶法僅離散控制量，以降低設計變量的個數；②為了獲得較精細的彈道，利用配點法和橢球聚合法將多目標彈道優化問題轉化為單目標的非線性規劃問題，利用非線性規劃算法進行求解，并進行節點自適應加密。

2.2 橢球聚合法

在上述混合求解策略中，利用非線性規劃求解多目標問題時，需要用聚合公式將多目標優化問題轉化為一組單目標優化問題。為了保持目標函數的連續性，本文采用橢球聚合公式[10]。該方法使用具有特定方向和較大偏心率的橢球(橢圓)與可達目標區域Ω的最優邊界相切，并尋找邊界上的切點，從而在一定條件下給出PF的近似。

對于極小化問題而言，在大多數情況下，PF是可達目標區域左下邊界?Ω的一部分。橢球聚合公式使用N個橢球(橢圓)與上述邊界?Ω相切。通過位于邊界?Ω上的切點給出PF的近似。該方法要求橢球具有一個較大的長軸和若干個較小的短軸。橢球的中心一般位于可達目標區域的左下側，通過控制橢球長軸的方向來獲得不同的邊界點，如圖2所示。在一般情況下，當長軸方向均勻分布時，橢球聚合法可以產生近似均勻分布的PF。具體的做法是：將長軸方向與一組均勻分布的權重矢量相關聯。

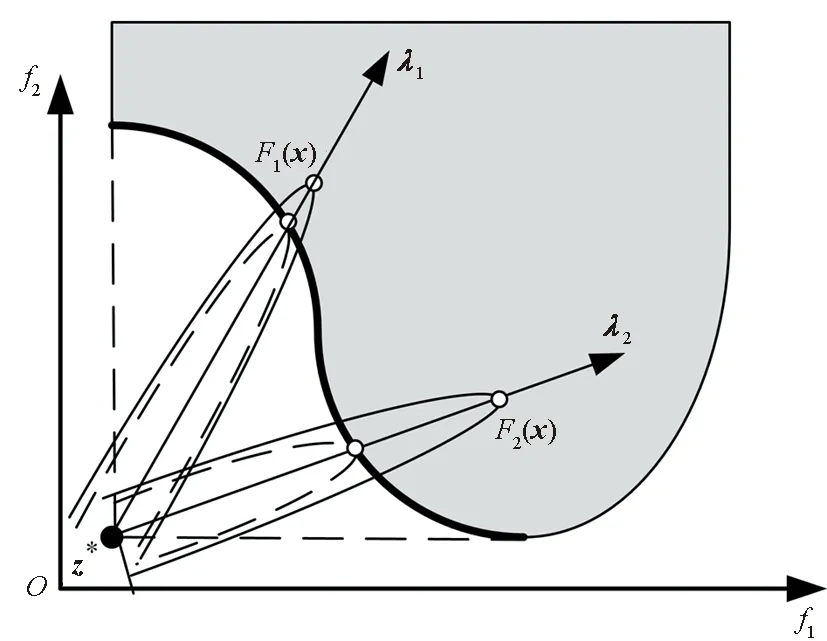
圖2 旋轉橢球方法Fig.2 Rotated ellipsoid method

根據上述思想，將多目標優化問題處理為N個單目標優化問題。令λ表示權重矢量，R(λ)表示將第一個目標函數F1的坐標軸旋轉到權重矢量λ方向的坐標變換矩陣。橢球與邊界?Ω的切點是式(10)所示單目標優化問題的全局最優解。

s.t.x∈Ω

(10)

其中，

(11)

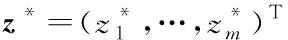
2.3 分解多目標進化算法

分解多目標進化算法MOEA/D由Zhang和Li于2007年提出[13]，該算法將多目標優化問題轉化為多個單目標優化子問題，對子問題采用進化算法以合作的方式同時進行優化。因此，其具有進化機制簡單、收斂速度快、PF近似均勻等優點。

以橢球聚合公式為例，將原始多目標優化問題分解成N個標量優化問題。令λ1, …,λN為均勻分布的一組權重矢量，z*為參考點，則第j個子問題的目標函數為

(12)

因為gRE關于λ連續，所以當權重矢量λi和λj相互接近時，子問題gRE(x|a,R(λi),z*)的優化解應該接近gRE(x|a,R(λj),z*)的優化解。因此與權重矢量λi相鄰的關于gRE的信息能夠對子問題gRE(x|a,R(λi),z*)的優化起到輔助作用。MOEA/D包括初始化、更新和停止三個過程，具體步驟見文獻[13]。

在MOEA/D中，通常采用歐式距離測量兩個權重矢量之間的鄰近性，并用于確定矢量λi的鄰居。獲得較為精確的參考點z*通常需要求解多個單目標優化問題，比較耗時，因此該算法首先進行初始化，然后在迭代過程中進行更新。這樣可以使得理想點的更新隨著迭代優化而進行，節省了計算時間。

2.4 自適應配點法

針對軌跡優化問題中精度和效率之間的矛盾，豐志偉等曾提出基于二代小波的節點自適應加密方法[9]。該方法采用Runge-Kutta方法將原軌跡優化問題轉化為非線性規劃問題，并采用非線性規劃算法求解；根據控制或狀態函數的小波系數幅值確定自適應加密的節點，并進行序列優化。

基于二代小波的節點自適應算法輸入參數包括：初始分辨率水平J0(控制初始節點個數)；最大分辨率水平Jmax(控制背景節點個數，即最小節點間隔)；小波系數幅值的閾值ε。終止條件：前后兩次節點位置相同或達到預定的迭代次數。計算流程如下：

1)根據初始分辨率J0生成均勻節點GJ0(或{τi})以及該均勻節點上的狀態函數x和控制函數u的初始猜測；

2)利用非線性規劃算法優化由原軌跡優化問題轉化得到的非線性規劃問題，得到狀態函數x和最優控制函數u；

3)根據節點自適應算法確定下一步優化的自適應節點，若存在多個控制函數，則將這些控制函數分別得到的自適應節點進行合并；

4)利用前一次優化計算的解x和u，利用小波插值計算新的自適應節點上的初始猜測，并進行循環迭代，直到滿足終止條件。

需要說明的是，小波系數幅值的閾值通常可取為ε=γ(umax-umin)。對于間斷函數，γ可取0.005～0.01；對于連續函數，γ可取0.001～0.005。

3 仿真分析

3.1 仿真條件和參數

以通用航空飛行器[14](Common Aero Vehicle，CAV)氣動性能為例進行多目標彈道優化，通過擬合可得到CAV-H模型的氣動系數

(13)

優化指標包括射程最大和總加熱量最小。考慮的約束條件包括駐點熱流密度、動壓、過載以及禁飛區約束，仿真參數設置如表1所示。

利用本文提出的混合優化算法，將攻角和側傾角離散為15個點，加上終端時間共31個設計變量。

在MOEA/D優化過程中采用旋轉橢球聚合公式，種群規模(子問題個數)為300，迭代步數為1000，鄰居規模為20。采用300個均勻分布的權重矢量，每個權重矢量的分量為正值，和為1。節點自適應算法中，為了節省時間，將優化子問題數目取為21，小波系數幅值的閾值取εi=0.001·(uimax-uimin)。針對每個子問題，取MOEA/D優化結果中相應權重系數對應的子問題的解(控制量和飛行時間)進行積分得到狀態變量，并作為配點法中的初始解。采用序列二次規劃算法SNOPT[15]求解非線性規劃問題。

表1 彈道優化約束條件

3.2 彈道約束條件處理

由于MOEA/D無法直接處理多目標彈道優化問題中存在的復雜非線性約束，需要對約束進行處理。對于不等式約束，在聚合目標gte(x|λ)中引入懲罰項，MOEA/D算法更新新解時不僅考慮了解的聚合目標，而且還融合了約束違約程度。采用罰函數的MOEA/D在求解控制-結構一體化設計中得到了成功應用[16]。

假設第i個約束gi(x)≤0,i=1,…,nc的違約度[17]定義為

Wi(x)=max[0,gi(x)],i=1,…,nc

(14)

如果Wi(x)=0，則x可行，否則不可行。將目標函數修改為

F′(x)=[f1(x)+aW,…，fm(x)+aW]T

=[f′1(x),…，f′m(x)]T

(15)

其中

W=max[W1,…,Wnc]

(16)

nc是約束的個數，參數a>0。

3.3 優化結果分析

利用進化算法得到的近似PF如圖3所示，從圖中可以看出，最大射程解在圖中以“▽”標示，此時射程為13 799 km，總加熱量為18 173 MJ/m2；最小總加熱量解以“△”標示，此時總加熱量為10 745 MJ/m2，射程為10 930 km。兩個目標具有明顯的沖突性，即射程最大時，總加熱量也最大，反之亦然。為了進一步對比分析，圖4給出了三條多目標優化典型彈道(兩條單目標最優彈道；一條典型折中解，圖3中以“□”標示)對應的控制量以及主要彈道參數。從圖4曲線可以看出，最大射程彈道的攻角為最大升阻比攻角；最小總加熱量彈道攻角較大，且高度在縱平面大幅跳躍。

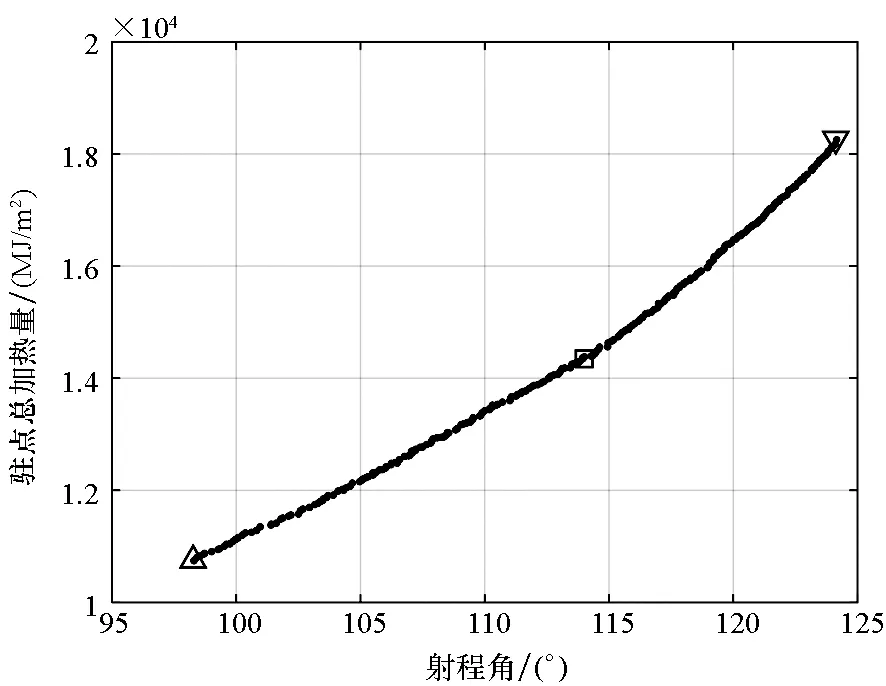
圖3 最大射程-最小總加熱量兩目標PFFig.3 PF for maximizing down range and minimizing total heating

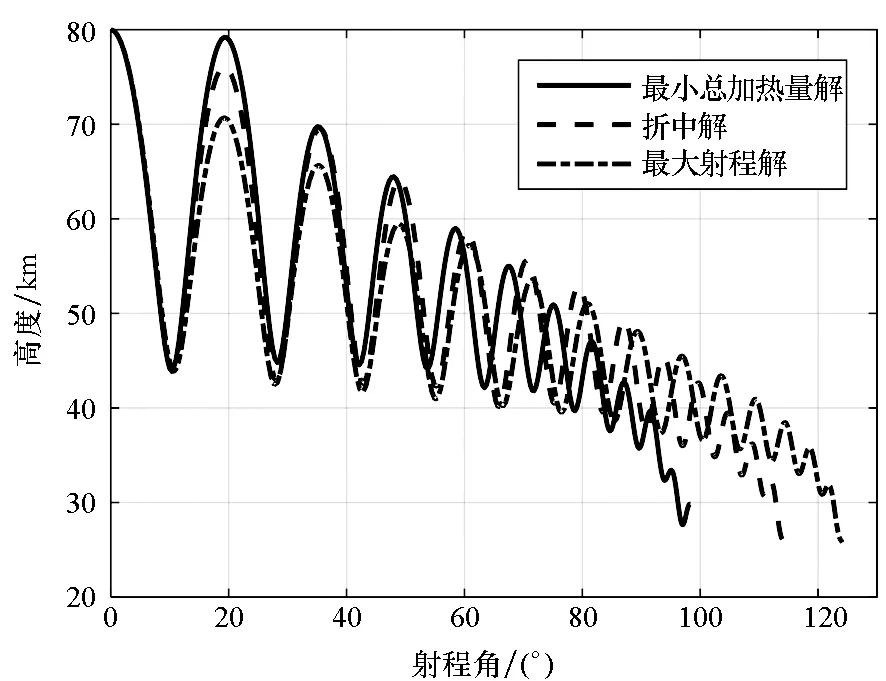
(a) 高度(a) Height

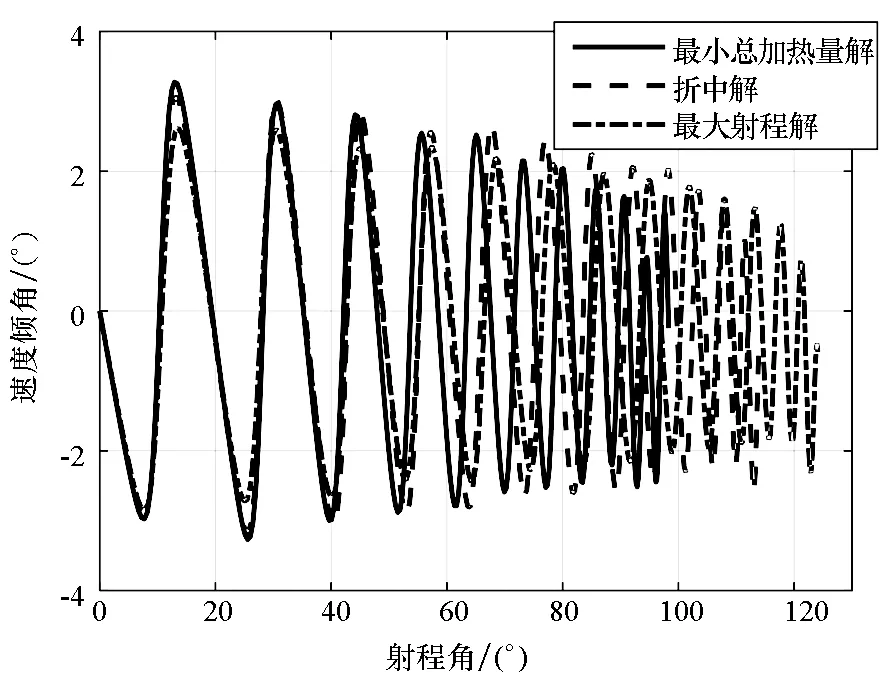
(b) 速度傾角(b) Velocity dip angle

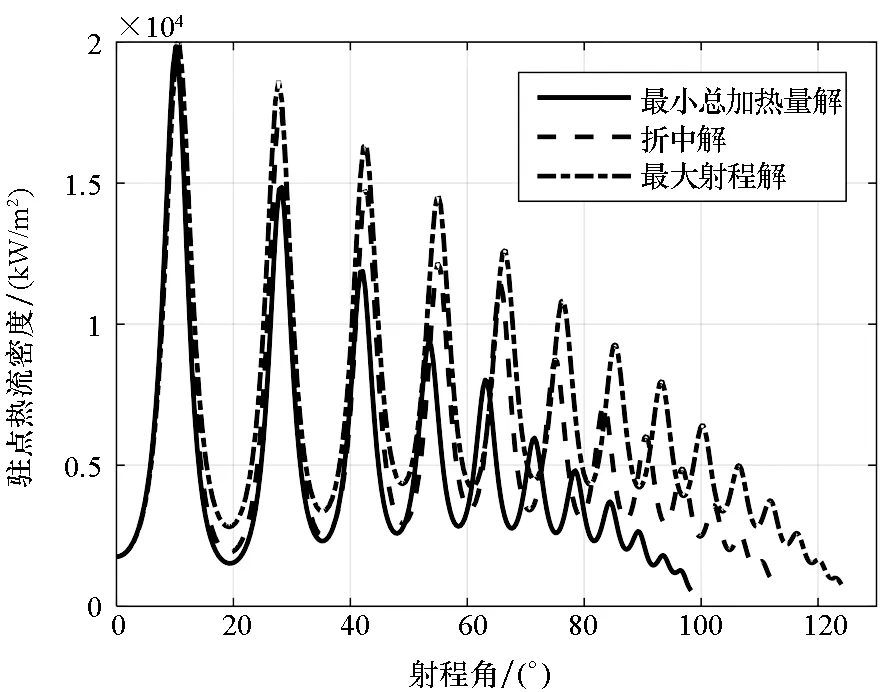
(c) 駐點熱流密度(c) Heating rate of stagnation point

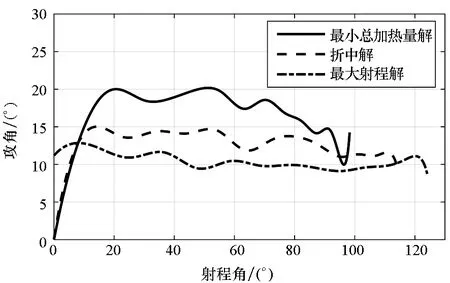
(d) 攻角(d) Attack angle

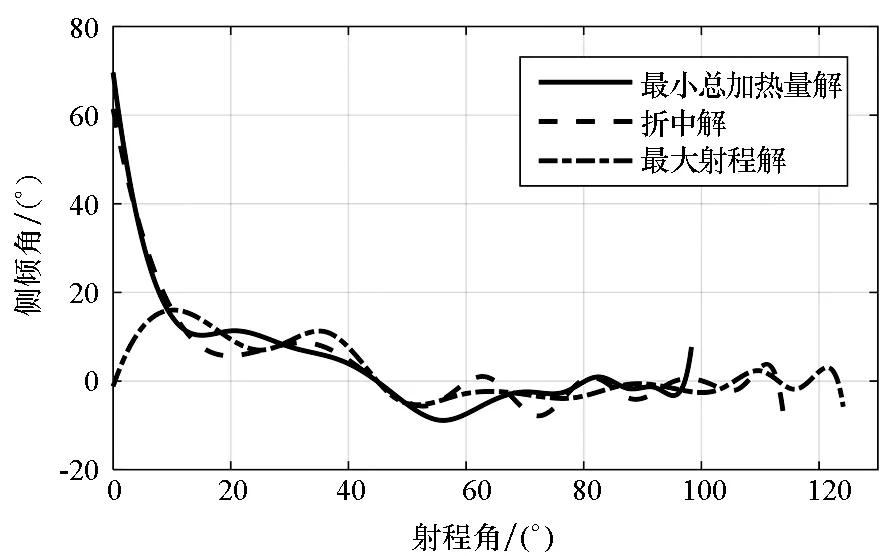
(e) 側傾角(e) Bank angle圖4 多目標優化彈道典型解(MOEA/D)Fig.4 Typical solutions of multiobjective trajectory optimization (MOEA/D)

采用自適應配點法優化得到的近似PF如圖5所示，與進化算法MOEA/D優化得到的近似PF相比，近似PF得到較好的改善。在最大射程解附近，MOEA/D較接近配點法獲得的解，而在最小總加熱量解附近其偏差較大。由此說明采用15個點近似攻角和側傾角來優化最大射程是足夠的，但是為了優化最小總加熱量彈道，需要增加設計變量的個數。

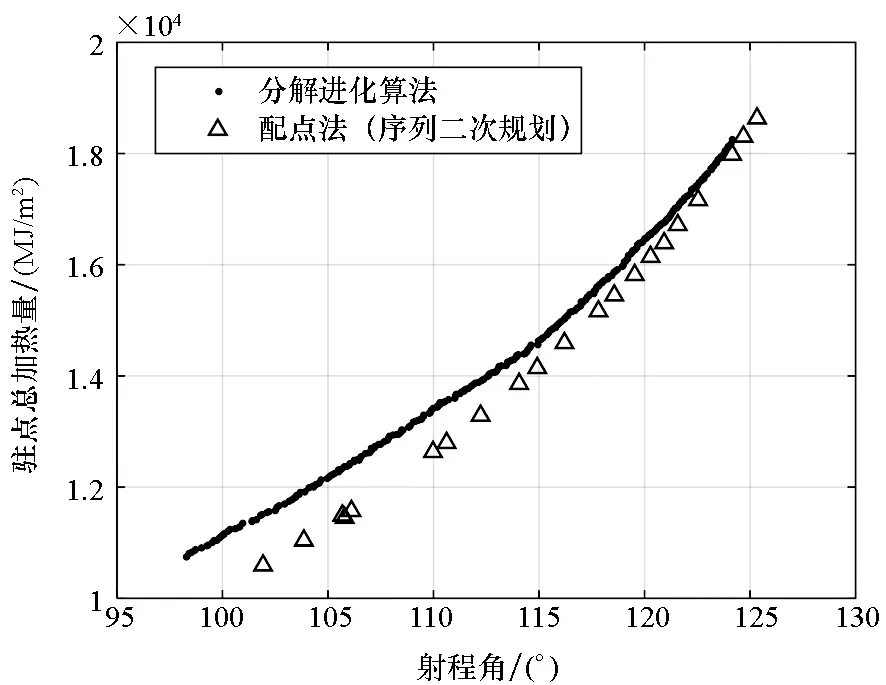
圖5 兩種方法的PF對比Fig.5 PF comparison of two methods

自適應配點法優化得到的攻角和側傾角曲線如圖6所示。整體規律與進化算法得到的解一致，但是最小總加熱量解攻角曲線更復雜。

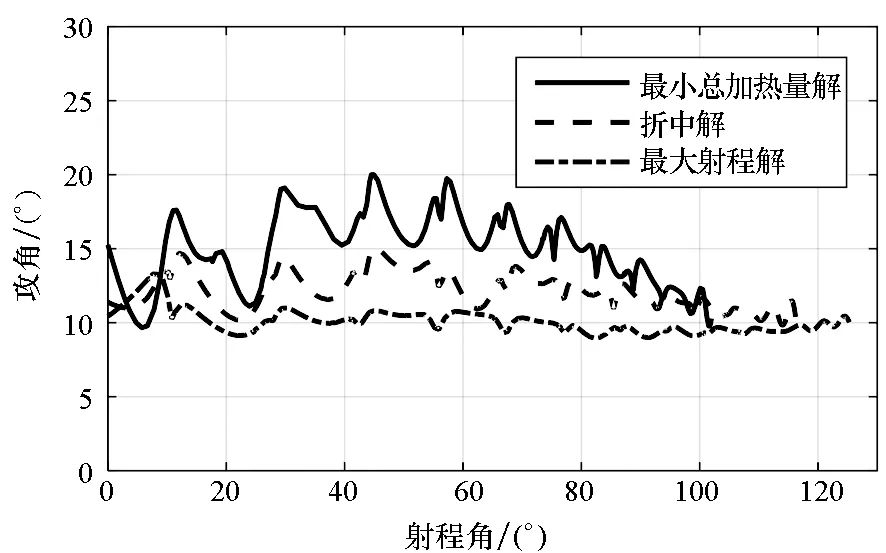
(a) 攻角(a) Attack angle

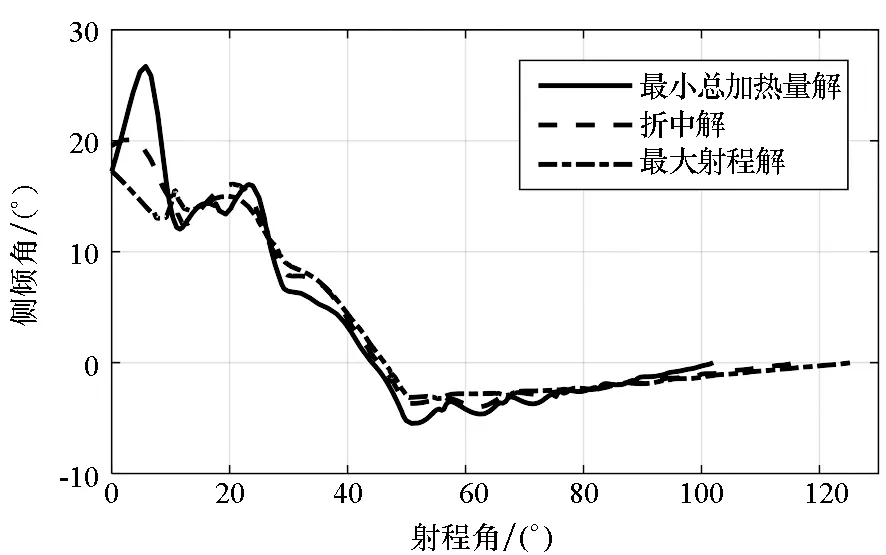
(b) 側傾角(b) Bank angle圖6 多目標優化彈道典型解(自適應配點法)Fig.6 Typical solutions of multiobjective trajectory optimization (adaptive collocation method)

4 結論

針對滑翔飛行器多目標彈道優化設計問題，綜合考慮計算效率和精度，結合分解多目標進化算法和自適應配點法提出一種分層、混合優化方法。以美國CAV-H為例進行仿真分析，計算結果驗證了所提混合優化方法的有效性，不論是MOEA/D還是配點法，均能夠得到較均勻分布的Pareto前沿。