海洋環境監測平行系統優化融合*
蘇振東,楊瑞平,王飛躍
(1. 中國科學院大學, 北京 100190; 2. 海軍研究院, 北京 100161)
兩個或兩個以上的海洋環境監測系統,以任務為牽引,以通信網絡為介質,有機組合成海洋環境監測體系。為認識和掌握海洋環境特點和變化規律,各級政府和各個部門都投入大量經費建立了形式多樣的海洋環境監測系統,由此形成了一個又一個的“煙囪”。一方面,造成了資源的極大浪費,另一方面,對海洋自然環境帶來了極大破壞。解決該問題的根本出路是:在國家層面,針對各海洋環境監測重點區域,統籌該區域的海洋環境監測系統建設,實現不同系統之間的資源信息共享,形成海洋環境監測體系。
海洋環境監測體系中的各個系統往往屬于不同的部門,難以同步開展建設,更難以一次性投資建成。因此,在各海洋環境監測系統建設之前,或者存在其他海洋環境監測系統的情況下建設新的海洋環境監測系統之前,海洋領域投資建設管理決策部門應站在全局角度,從體系優化的角度對各個系統的能力進行統籌,在統籌的基礎上提出新系統的建設方案,既滿足各個部門對本單位投資建設海洋環境監測系統的能力期望,同時盡可能避免出現監測區域過度重疊、監測能力過度重復的現象。要實現對各個系統的統籌,應搭建各個海洋環境監測系統建設方案的平行系統,形成海洋環境平行監測體系,具體的方案策略在文獻[1]中有詳細描述,這里不再贅述。本文在海洋環境平行監測體系運行基礎上,構建優化融合模型對各個海洋環境監測系統進行優化融合和體系評價,使海洋環境監測體系的各個系統在滿足預定能力要求的基礎上,盡量減少節點數量和觀測設備的數量,以節約整體資源和運行成本。
1 基本思路
首先,分析不同海洋環境監測系統建設方案,對這些方案的覆蓋區域、設施設備和網絡連接等進行簡單的疊加,形成初始海洋環境監測體系。然后,構建初始海洋環境監測體系的平行系統,形成海洋環境平行監測體系。接著,將海洋環境平行監測體系劃分為明確功能區別的各個子系統,每個子系統包含對應的設備。進一步,以體系和其中的這些子系統為基礎開展系統優化融合。優化融合為最優體系并對優化融合結果進行評價,在體系層面優化海洋監測資源分配方案,同時確保優化融合后的各個系統監測效能不降低,并減少運行成本。
在系統優化融合過程中引入熵方法以追求系統的有序性,用熵值法得出各個系統的權重。最后,運用線性規劃得到不同設備在優化融合后的海洋環境平行監測體系中所占的比重,也就得到了優化融合后的海洋環境平行監測體系中各種監測設備類型和數量分配的方案。
熵是系統無序程度的度量,熵方法在決策融合與信息融合有關的問題中有著較為廣泛的應用。文獻[2]使用熵方法實現傳感器系統的決策融合以及導航系統的信息融合,使用系統融合率來表征融合系統的信息利用率,通過求聯合熵的最小值點來確定系統融合率的最大值點,最終推導出信息利用率最高的融合算法。文獻[3]使用熵方法進行非線性融合體系的評測,使用熵理論系統構建媒體融合的指標體系,并采用熵值法確定融合體系中不同維度的權重,最終獲得各地區的融媒體發展指數。而隨著機器視覺的興起,文獻[4]將熵方法應用到圖像合成領域。考慮海洋監測體系的特點,可采用線性系統方法對其進行融合并利用熵方法進行評價。
2 體系融合模型
2.1 體系融合熵的概念
體系融合熵是基于普通物理學中的概念以及管理熵的相關定義,結合體系融合的特點而提出,是指在多個系統融合為體系的過程中,由于系統優化融合導致體系的有序性或無序性增大或減小的一種度量方式。熵的增加代表體系無序性的增加,反之則代表體系無序性的減小。確認系統融合為最優結構體系的依據是找到體系融合熵為最小值時的體系結構。
對于非線性體系,體系內各系統之間存在著非線性關系,很難依據熵的特征進行精確計算。海洋環境監測體系中各系統的線性關系強于非線性關系,故可以根據各系統的觀測數據,采用熵方法構建系統優化融合模型。
系統的發展存在著階段性和區域性差異,系統優化融合并不是要替代體系中的各系統。系統越成熟,其構成越復雜,系統內部熵值越大。另外,體系內不同系統的熵也不相同,受到其他系統影響越大、越傳統的系統熵值越大;反之,受其他系統影響不大、善于獨立完成任務的系統熵值較小[4]。
體系在熵值增加過程中之所以能夠得以穩定持續發展,主要得益于體系在不斷地完善與豐富,帶來的負熵輸入不斷增大,系統調適能力也逐步增強。目前的體系評價方法有層次分析法、“三域”影響力評測法和熵值法等。熵值法在某種程度上可以盡量避免出現評價時指標權重主觀偏向的問題,可以很好地反映負熵的輸入情況[3]。
利用熵值法可以較好地確定評價指標體系的權重,從而計算出各維度和各項指標的評價得分。計算過程大體包括如下幾步: 一是指標無量綱化處理,二是通過信息熵公式計算出信息熵值,三是根據信息熵值計算效用值,四是根據效用值計算各維度和各指標權重,五是根據指標權重計算各維度和各項指標的最終得分。
2.2 海洋環境監測體系優化模型
圖1給出了系統優化融合模型的流程框圖。
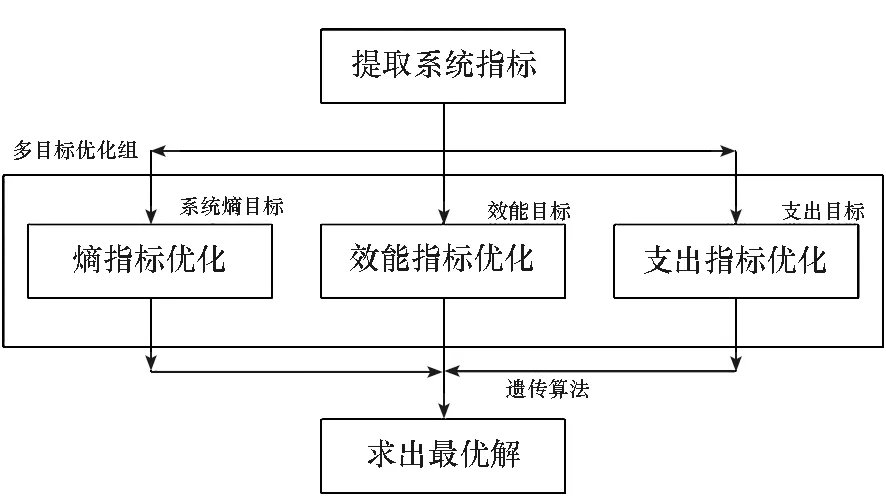
圖1 系統優化融合模型流程框圖Fig.1 Flow chart of system optimization fusion model
系統優化融合可以從體系熵、體系效能與體系支出三個不同的角度進行分析。
2.2.1 基于體系熵的分析
在海洋環境監測系統優化融合過程中,并不是每一種環境監測設備都會一直啟用,也并不是每一種啟用的設備都會一直采取簡并模式(即各系統共用一套監測設備,各自提取出自己需要的數據)。設第n種監測設備啟用的概率為pn(0≤pn≤1),在第n種監測設備啟用的情況下采用簡并模式的概率為qn(0≤qn≤1)。
體系熵值的數學模型為:
(1)
式中:S0表示體系的熵值;1≤h≤r,r為該體系中啟用的監測設備的數量;Kh為每種設備的權重;Sh為該種設備產生的熵值。
根據熵值的定義,一個對象的熵值S可表示為:
(2)
式中,n為該對象所擁有狀態的總數,Pi表示第i個狀態出現的概率。
對監測設備的狀態進行分析,每個監測設備都存在三種狀態:不啟用;啟用且采用簡并模式;啟用但不采用簡并模式。由此可將熵值Sh表示為:
Sh=-{phqhln(phqh)+ph(1-qh)ln[ph(1-qh)]+(1-ph)ln(1-ph)}
(3)
以K0表示體系運行時的熵系數,綜合式(1)~(3),體系的熵值即可表示為:
(4)
2.2.2 基于體系效能與體系支出的分析
假設該監測體系中有k個系統需要進行優化融合,體系中能實現某一功能的監測設備有l種。
對于第n型監測設備,采用該型設備的各個系統,其觀測的區域多多少少會有所重疊,所以在計算總效能時,需要去掉各個系統效能中重疊的部分,即冗余效能。分析體系效能如下:冗余效能為Cn,即各個監測系統使用此型設備時,共同需要的數據與結果及其帶來的收益;在采用簡并方案時,第m個系統使用此型設備所產生的效能為An,m;在不采用簡并方案,所有系統使用各自的設備觀測時,第m個系統使用此型設備所產生的效能為Bn,m;在不啟用時,該型設備產生的效能為0。該型設備在不同情況下產生的效能乘以該情況的啟用概率之后相加,得到該型監測設備產生的效能的數學期望Wn;所有的監測設備產生效能的數學期望之和,即為體系融合后的總效能E。
對于第n型設備,在使用簡并方案時,可認為整個體系共用一套該型設備;而不采用簡并方案時,體系中每一個需要使用該型設備的系統均使用各自的一套該型設備。分析體系中支出如下:在采用簡并方案時,使用此型設備的支出為Dn;在不采用簡并方案,所有系統使用各自的設備進行觀測時,第m個系統的支出為En,m;在不啟用時,該型設備產生的支出為0。該型設備在各種情況下運轉支出乘以該情況的發生概率之后相加,即得到該型設備運轉支出的數學期望Fn;所有設備支出的數學期望之和為融合后體系的總支出F。
根據以上假設參數,圖2~4給出了體系總效能與總支出的計算流程及計算框圖。
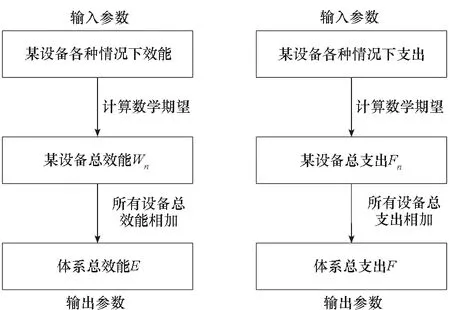
(a) 體系效能(a) Systems efficiency (b) 體系支出(b) Systems expenditure圖2 體系效能與支出計算流程圖Fig.2 Flow chart of system efficiency and expenditure calculation
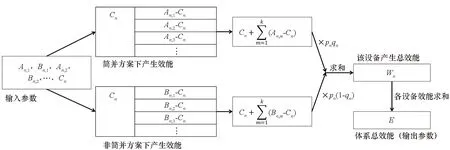
圖3 體系總效能計算框圖Fig.3 Block diagram for calculating the total effectiveness of the systems
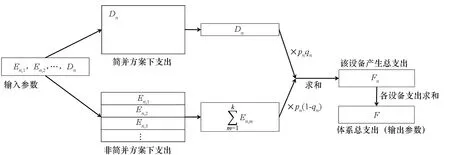
圖4 體系總支出計算框圖Fig.4 Block diagram for the total expenditure calculation of the systems
根據以上框圖,可以得到如下數學模型:
1)體系總效能的數學模型:
(5)
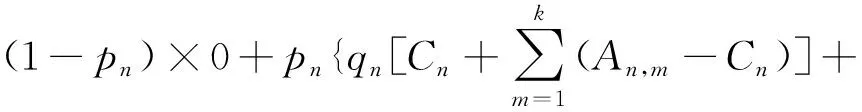
(6)
2)體系總支出的數學模型:
(7)
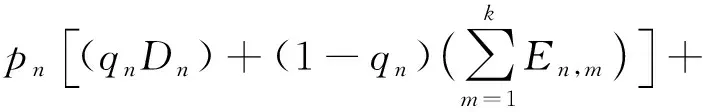
(1-pn)×0
(8)
3 多目標融合分析
海洋環境監測系統優化融合為最優時,體系熵與體系總支出最小,且達到體系總效能最大。 因此建立式(9)所示基本模型:
(9)
輸入各類參數,則可以計算出在熵最小的基礎上實現系統優化融合的最優解。
在多個系統的優化融合中,考慮同一目標或功能會用不同的設備實現,故把每個系統均拆分成若干能實現不同功能的功能單元。而系統優化融合實質上也是各個系統功能相近或相同的功能單元的融合,所以以下的分析均以各個系統的某一功能單元為對象進行分析。考慮系統的支出主要體現在運行設備時消耗的資源以及維護設備時所需的人力物力等運行及維護成本,所以下文中用成本來代表系統的支出。
融合后的功能單元中,假設所有的設備照常運行,觀測結果則來自多個設備觀測結果的決策融合。
設qi為該功能單元采用簡并模式的概率,則該功能單元的成本可表示為:
(10)
其中,Di表示進行簡并模式時該單元的成本,Ei表示不進行簡并模式時該單元的成本。 顯而易見,Di 熵是系統無序程度的度量,信息熵值法可以用來判斷某指標的離散程度[2],對以該指標為中心的系統做出資源等的分配指導。 設某一待評價體系有m個指標,有n個樣本值,則指標數據矩陣為B=(bij)m×n。 對于每一個指標,樣本值的波動越大,最終得到的熵值也越大,即表明樣本值的影響因素越多,則對其進行資源分配也有更大的意義;反之,如果某一指標的所有樣本值都相等,則對其進行資源分配也就失去了意義。 熵值法評價的一般過程如下: 1)對各指標同度量化以方便計算第j項指標下的第i個指標值的比重pij: (11) 2)計算熵值ej: (12) 3)計算第j項效用值。 對一項指標,指標的波動越小,熵值就越小,對應的效應值就越小,所以有: gj=1-ej (13) 4)確定權重: (14) 5)綜合評價值: (15) 在效能與熵方面,考慮系統優化融合前各個系統建設方案有所不同,選用的設備的靈敏度與精確度等也各自不同。從文獻[4]中可知:對同一目標的組合觀測系統,用盡可能多的子系統來進行融合,能獲得更多的觀測信息;而且,當各子系統提供的信息相關性越小、信息的利用率越高時,系統輸出的不確定度就越小,觀測信息的隨機性也越小。也就是說:在體系融合過程中,既要通過多系統進行體系融合獲得更多的信息,又要通過合理分配,提高獲得的信息質量。所以,對于海洋環境監測體系來說,可以通過設定不同的參考權重來調整體系監測能力,提高監測信息質量。 可以證明,海洋環境監測體系通過Shannon信息熵函數處理后得出的決策方案的正確率與觀測概率以及影響權的分布有直接關系[5],而信息熵函數的求解和處理過程是一個引入負熵的過程[6]。不妨將信息熵函數的求解過程以下面的形式進行簡化。 設一個功能單元分為m個維度,代表這個功能單元所實現功能的不同方面,如可用相似設備觀測風速和風向兩方面。引入效能指標,以一個常數代表某種設備實現這一功能的能力,其中越高的效能指標即代表此設備在這方面觀測可取得的精確度及靈敏度等越高。而這種效能指標需要在科學詳細的評判標準下,在設備的靈敏度和精確度的基礎上進行人工評定[7]。不妨設體系中有三個功能單元,能力維度分為兩種,融合前體系效能指標的矩陣設定如下: (16) 通過式(11)~(14)的過程可得到該單元的維度權重為: a=(a1,a2) (17) 其中,熵值表示該維度的無序程度。引入性能更佳的設備進入該體系,可以為體系引入負熵,以增加體系的穩定性。 設三個系統的決策影響權為: W=(w1,w2,w3) (18) 則融合后的體系功能指標為: w1(a1b11+a2b12)+w2(a1b21+a2b22)+ w3(a1b31+a2b32) (19) 兩個維度的功能指標分別為: (b11w1+b21w2+b31w3,b12w1+b22w2+b32w3) (20) 將體系的總功能指標最大化作為目標、將體系兩個維度的功能指標分別到達某一值作為約束條件即可進行線性規劃,從而得出在僅考慮效能的情況下最佳的決策影響權值。在實際設計過程中,決策影響權高的系統可作為融合中心;決策影響權低的系統可以減少運行的頻率,甚至待機,其觀測數據一般用作印證。 若將兩個功能維度的最小功能指標設置為: Mmin=(m1,m2) (21) 則整體要求可設置為以下條件: (22) 基于以上條件可求得最佳的決策影響權為: Wbest=(w1best,w2best,w3best) (23) 以此作為系統融合的權重,可以求出融合后系統處于簡并模式下的成本。 在此處,權重的分配對應在現實中可以是監測系統資源的獲得量。權重高的系統分配到較多的資源,而權重小的系統僅分配維持運行的資源以及緊急使用的資源。設系統i在該功能單元簡并模式下的成本為系統i的權重wi與系統i單獨運行的成本Ei的函數Di(wi,Ei),則成本計算有以下結果: (24) 而節省的比例則為: (25) 也可以從成本最小化的角度進行規劃: (26) 由此最終亦可求得合適的決策影響權重。 從成本、效益、熵值等方面對系統優化融合進行建模與分析,并提出了一套基于熵值法和線性規劃的系統優化融合方案。基于此方案的分析,系統設計時的目標導向對系統建設方案會產生很大影響,所以在系統優化融合前應盡量做好各個系統建設方案的評估與分析,明確各個系統的功能和側重點,盡可能提高體系的效能指標,降低系統的能力冗余度。4 熵值法體系優化
4.1 熵值法評價
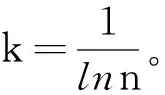
4.2 體系優化
5 結論

