基于組合近似模型的城市客車車架輕量化研究*
趙東偉, 尹懷仙, 張洪信, 趙清海, 付磊
(青島大學 機電工程學院, 山東 青島 266071)
車架作為城市客車的核心零部件之一,是基本的承載、連接件,有著較大的質量占比。試驗表明,汽車整備質量減少10%,能量消耗減少6%~8%,續航能力、轉向靈活性等也得到提高。因此,在滿足客車車架強度、剛度要求的前提下對車架進行輕量化十分必要。
由于傳統的有限元優化分析方法計算量大、效率低,通常建立近似模型代替原始模型來處理復雜工程的結構優化問題。目前大多數研究是從多種近似模型中選擇擬合精度最好的模型進行結構優化,對于復雜機械優化問題,各種近似模型對各種狀態變量的預測能力表現各異,在優化設計中選取單一近似模型易造成局部最優。如Pan F.等利用單一的支持向量回歸近似模型對目標函數進行優化迭代,其不能保證約束函數的全局精度;Chen S. K.等基于Kriging近似模型和水平集表征法對響應的不確定區域進行量化,其對試驗設計采集的樣本數依賴性較大,可能導致結果局部最優。因此,該文以某混合動力城市客車底盤車架為研究對象,通過對響應面、徑向基神經網絡、克里格及正交多項式4種近似模型的預測能力的對比分析,按照一定的權系數線性疊加建立組合近似模型,對城市客車車架進行結構輕量化優化設計,驗證組合近似模型在城市客車車架輕量化設計中的可靠性。
1 建立近似模型
近似模型是通過建立相應數學模型來近似模擬一組激勵參數與響應參數之間的關系,以精確擬合實際模型。其建立流程見圖1。

圖1 近似模型建立流程
1.1 徑向基神經網絡模型
徑向基神經網絡(RBF)以待測點與樣本點之間的歐幾里得距離為自變量,即假設x1,…,xN∈Ω?RN代表一組基函數的輸入變量:
gi≡g(‖x-xi‖c)∈R(i=1,…,N)
(1)

徑向基函數的基本形式為:
(2)

1.2 響應面模型
響應面模型(RSM)基于數理統計技術,利用多項式函數擬合設計空間,具有計算效率高、適用范圍廣和魯棒性好等優點。其基本形式為:
(3)
式中:xi為第i個設計分量;α0,αi,αij,αii,αijk,…,αii…i為多項式待定系數;d為響應面的最高階數。
1.3 正交多項式模型
當試驗因素較多時,采用最小二乘法求響應面模型參數的計算過程相當復雜,可采用正交多項式擬合響應面模型(Chebyshev)使計算過程簡化,同時彌補使用最小二乘法求系數過程中的不足。
1.4 克里格模型
克里格方法(Kriging)是基于變異函數理論和結構分析,在規定區域內對區域化變量取值,并進行無偏、最優估計的一種空間局部內插方法。其基本表達式為:
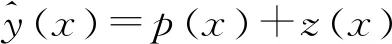
(4)
式中:p(x)為最基本的多項式;z(x)為均值為零的隨機項,通常取高斯函數作為相關函數。
1.5 組合近似模型
組合近似模型(EM)由多個近似模型(如多項式、徑向基函數、克里格和正交多項式等)加權線性疊加構成。其一般表達式為:
(5)
式中:yEN為組合近似模型的響應預測值;M為單一近似模型的個數;ωi、yi分別為第i個模型的權系數和響應預測值;設計變量x為矢量。
式(5)中權系數之和等于1。組合近似模型的關鍵是計算權重系數。采用啟發式方法計算權重系數的公式如下:
(6)
(7)
(8)

2 單一近似模型精度分析
2.1 車架有限元模型
根據城市客車的二維圖紙,利用CATIA軟件構建車架幾何模型并以IGES文件儲存,導入有限元分析軟件ANSYS中。網格單元尺寸為10 mm。劃分網格后的車架網格單元為255 727個,節點為257 049個(見圖2)。

圖2 客車車架有限元模型
2.2 設計變量與響應的確定
車架輕量化設計中必須保證車架強度滿足要求。以車架所受最大應力和總質量為響應量,選取車架中9個板料的厚度為設計變量(見圖3),按照工程常用鋼板厚度將X1~X9的取值范圍設定為2~20 mm。

圖3 設計變量的選取
2.3 最優拉丁超立方試驗設計
對9個設計變量采用最優拉丁超立方試驗設計產生樣本點。最優拉丁超立方設計改進了隨機拉丁超立方設計的均勻性,使所有試驗點盡量均勻分布在設計空間,使因子和響應的擬合更精確真實。抽取200組試驗樣本組成試驗設計矩陣(見表1)。
2.4 近似模型擬合效果分析
從響應擬合效果圖可直觀地看出近似模型的精度高低,響應擬合效果圖中縱坐標為有限元分析得到的仿真計算值,橫坐標為同一樣本點通過近似模型預測的響應值,對角線代表真實的適應度,殘差為零。采集的樣本點落在對角線或其附近越多,則響應的預測精度越好。確定性系數R2和均方根誤差RMSE反映近似模型的整體精度,其計算公式分別見式(9)、式(10)。要求R2≥0.9、RMSE≤0.2。

表1 試驗設計數據 mm
(9)
(10)

以車架各主要承載梁X1~X9的厚度為優化輸入變量、車架使用性能相關參數(總質量和最大應力)為優化輸出變量,根據表1中樣本點對4種近似模型的擬合效果進行分析。徑向基神經網絡近似模型的擬合效果和精度分別見圖4、表2,響應面近似模型的擬合效果和精度分別見圖5、表3,正交多項式近似模型的擬合效果和精度分別見圖6、表4,克里格近似模型的擬合效果和精度分別見圖7、表5。
由圖4~7、表2~5可知:正交多項式近似模型中最大應力響應的確定性系數小于0.9,不能代替有限元模型進行計算;其他3種模型的精度符合要求,均可代替有限元模型進行后續優化設計。就響應的整體精度而言,克里格和響應面近似模型的整體精度最高;就車架最大應力響應的擬合精度而言,克里格近似模型的精度最好;就車架總質量響應的擬合精度而言,響應面和正交多項式近似模型的預測精度最高,克里格近似模型與之相比略有下降。綜上,選取克里格和響應面模型構建車架最大應力和總質量的組合近似模型。

圖4 徑向基神經網絡近似模型各響應的擬合效果

項目RMSER2最大應力總質量0.068 790.002 980.935 520.989 84

圖5 響應面近似模型各響應的擬合效果

項目RMSER2最大應力總質量0.012 130.003 280.971 260.999 81

圖6 正交多項式近似模型各響應的擬合效果

項目RMSER2最大應力總質量0.097 880.002 510.897 590.999 86
3 基于組合近似模型的車架輕量化設計
3.1 權系數的確定
采用啟發式計算法,針對不同響應,根據式(6)~(8)計算組合近似模型中各單一近似模型的權系數,結果見表6。
利用單一近似模型的權系數構建組合近似模型,并對其擬合效果進行分析,結果見圖8。
由圖8可知:有限元仿真值和組合近似模型的預測值誤差較小,預測精度略高于單一近似模型,且適合各種狀態變量的預估。因此,可采用該組合近似模型代替有限元模型進行優化計算。
3.2 優化數學模型
以車架的最大應力和變形為約束、質量最小為目標的優化數學模型可定義為:

項目RMSER2最大應力總質量0.005 720.017 600.999 300.989 57

表6 近似模型的權系數

圖8 組合近似模型各響應的擬合效果
(11)
式中:M(X)為車架的總質量;X為設計變量的可行域,X=[X1,X2,X3,X4,X5,X6,X7,X8,X9];Δrmax(X)為車架的剛度變形,其最大值為0.06 m;λ為強度安全系數,λ=1.5;σmax為車架受到的最大應力;σs為材料的屈服強度,σs=345 MPa。
3.3 模型求解
采用霍克-吉維斯直接搜索法在優化空間中尋找全局最優解。組合近似模型優化前后各設計變量的比較見表7。

表7 優化前后各設計變量對比
對優化后車架重新建立有限元模型進行分析,結果顯示:優化后車架質量為865 kg,比優化前的989 kg減輕12.54%;優化后車架的最大應力由187 MPa增至214 MPa(見圖9),安全系數達到1.6,滿足設計要求。

圖9 優化前后車架等效應力(單位:Pa)
4 結論
(1) 比較響應面、徑向基神經網絡、克里格及正交多項式4種近似模型對車架狀態變量的估算精度,克里格近似模型對最大應力的估算精度最高,響應面近似模型對總質量的估算精度最高。
(2) 基于克里格和響應面近似模型構建的車架狀態變量估算組合近似模型對各類狀態變量都有較高的估算精度,將其用于車架輕量化設計,與優化前車架相比,優化后車架減輕12.54%,優化目標得以實現;雖然應力有所增大,安全系數有所減小,但都在合理范圍內。

