基于遺傳算法優化神經網絡的智能配電網線損計算研究

胡偉楠 王劍飛 何志滿 何國超 劉偉 付紹鑫 蔣新川 張琳

摘 要：為實現結構復雜、低壓臺區智能配電網的線損計算，首先構建誤差反向傳播（BP）神經網絡模型以計算配電網理論線損，然后利用遺傳算法（GA）深度優化神經網絡并建立GA-BP模型。基于上述模型計算配電網的理論線損率并對模型計算性能進行比對分析。結果表明，使用GA-BP模型進行線損計算比單一BP模型計算的平均絕對誤差減少約0.273%。應用遺傳算法優化后的神經網絡線損率計算模型較單一BP神經網絡模型具有更好的非線性擬合能力和更高的計算精度。

關鍵詞：神經網絡;遺傳算法;智能配電網;優化;理論線損;擬合

中圖分類號：TP39文獻標識碼：A文章編號：2095-1302（2020）01-00-04

0 引 言

配電網線損指配電線上的電能損失，通常包括理論線損和統計線損[1]。前者指電力系統中各元件造成的損耗，可以通過理論計算得出;后者為電網供電量和售電量的差值。造成配電網統計線損的原因包括[2]電阻作用造成的銅損、磁場作用造成的鐵損和管理方面導致的管理損耗等。通過分析比較理論線損和統計線損，可以在一定程度上反應配電網的內在運行和管理機制。線損率是線損分析中的一個重要指標，是網絡損失電量在供電總量中的占比，通常用百分比表示。國網重慶市電力公司2018年全年供電量約8.224 5×1010 kW·h，若線損率下降0.1%，全年損失電量可減少8.2×107 kW·h，按0.5元/度的電價，相當于減少經濟損失約4 100萬元。

常用的配電網理論線損率計算方法有[3-5]等值模型算法如均方根電流法、電壓損失法、最大電流法等，潮流改進算法如PQ分解法、改進迭代法、前推回代法等，隨著機器學習（Machine Learning，ML）技術的發展，出現了模糊識別算法和神經網絡算法，這些算法各有優缺點，可適應于不同的場景。但目前常用的線損率計算法多適用于35 kV及以上的配電網，低壓配電網線損率的計算不準確。

隨著電力系統的發展，配電網的數據采集量、網絡信息量越來越大，對于傳統計算方法而言，信息量的擴大會使計算難度增大[6];而機器學習方法本身需要大量數據來進行學習，數據量越大越有利于模型的建立，且計算精度更高。因此，采用機器學習來建立配電網線損率計算模型可以很好地解決配電網結構復雜、數據量偏大等難題。人工神經網絡（Artificial Neural Network，ANN）是機器學習眾多算法中的一類，ANN通過模擬人的大腦神經元的工作方式處理復雜、并行、非線性問題，由于人工神經網絡魯棒性強、容錯性好、擬合性能高，其在各領域得到了廣泛的應用[7]。目前人工神經網絡在線損率計算方面的研究不多，文獻[8]對神經網絡算法在配電網線損計算中的應用進行了討論，闡述了其在配電網線損計算中的優勢;文獻[9-10]利用神經網絡構建了簡單的配電網線損計算模型，以實例數據做了分析計算;文獻[11]針對5個電氣特征指標建立了10 kV配電網理論線損BP神經網絡預測模型，并采用粒子群算法對神經網絡進行了優化，為開展智能配電網線損率計算領域的深入研究奠定了框架基礎。

本文基于配電網實際運行數據，利用神經網絡對配電網線損率進行計算，并研究神經網絡在線損率計算中的效果;采用遺傳算法對神經網絡進行優化，從而實現提高配電網線損率計算模型精度的目的。

1 仿真模型

1.1 神經網絡模型（BP模型）

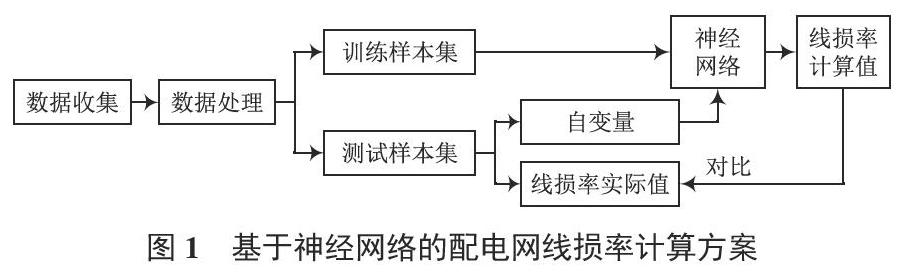
神經網絡計算線損率的方案如圖1所示。通過采集大量電網數據，在對數據進行歸一化處理后將數據集分為訓練樣本和測試樣本，然后對訓練樣本集進行訓練，得到神經網絡，再將測試樣本集中的自變量放入訓練好的神經網絡中，得到線損率，將計算的線損率和實際線損率進行對比，從而測試網絡的擬合性能。

本文采用使用最廣泛的BP（Back Propagation）神經網絡，即基于誤差反向傳播算法的多層前饋網絡，BP神經網絡的學習算法由前向傳播（計算誤差）和反向傳播（調整權值、閾值）組成。BP算法具有強大的非線性函數關系擬合能力，能夠有效處理特征參數和配電網線損率之間的非線性關系[12-13]。仿真模型利用Matlab（Matlab 2017b，MathWorks公司）神經網絡工具箱（Neuralnetwork Toolbox）設計神經網絡結構，構建基于BP神經網絡的線損率計算模型，即BP模型。

1.1.1 特征參數

神經網絡計算配電網線損率，首先需要確定決定配電網線損的特征參數。配電網臺區的損耗為：

式中：n為該臺區的分支數;i表示第i個分支;Ui為第i個分支在T時間內的平均電壓;WPi是第i分支末端消耗的有功功率;WQi為第i分支末端消耗的無功功率;Ri為第i分支的電阻。

在正常運行情況下，一個臺區負荷側的平均電壓和電阻都可以認為是不變的，臺區損耗的表達式可以簡化為損耗與有功功率WPi、無功功率WQi的關系。由此將配電網各臺區的有功功率和無功功率作為BP模型的特征參數，而線損率作為模型的輸出。

1.1.2 數據的獲取與處理

本文采用文獻[10]中甘南供電公司110 kV合作變10 kV饋線115城卡線同期月電量數據，包括該條線路上8個臺區的月有功功率、月無功功率以及該條線路的月線損率，其中，臺區的有功功率和無功功率數值較大，為去除量綱影響、加快網絡收斂速度，需要對原始數據進行歸一化處理，調用Matlab歸一化函數將特征參數轉換為方差為1、均值為0的標準數據，從而構成一個17×72的訓練樣本集。測試集包括該條線路上連續6天的日有功功率、無功功率以及線損率，同樣對自變量樣本數據進行歸一化處理，得到一個17×6的測試樣本集。

1.1.3 網絡結構

由于輸入數據包括8個臺區的有功功率和無功功率，因此BP神經網絡的輸入層神經元個數確定為16;中間層神經元個數通過經驗公式（2）確定，故取隱含層神經元個數l=log216=4;輸出為該條配電線路的線損率，神經元個數為1，由此可以確定神經網絡結構為16-4-1型，如圖2所示，圖中ω為各層之間的權值，b為各層閾值。

式中：l為隱含層神經元個數;n為輸入層神經元的個數。

1.2 遺傳算法優化神經網絡模型（GA-BP模型）

由于BP神經網絡的初始權值和閾值在[0，1]之間隨機產生，因此每次重新訓練得到的結果都不一樣，往往需要多次訓練之后選擇一個擬合較好的網絡;BP神經網絡自身還存在一定的局限性，容易陷入局部最優[14-15]。遺傳算法（Genetic Algorithm，GA）是一種全局尋優算法，通過模擬自然界“適者生存”原則，將原始種群經過選擇、交叉和變異操作后產生新一代適應度更高的種群[16]。本文采用遺傳算法對BP模型的初始權值和閾值初值進行優化，從而構建起GA優化BP神經網絡的線損率計算模型，即GA-BP模型，該模型的算法流程如圖3所示。

1.2.1 適應度函數

適應度（Fitness）表示遺傳算法中種群個體的優劣程度，本文采用線損率計算值與實際值誤差平方和的倒數作為個體適應度函數，表達式如下：

式中：y（k）為GA-BP模型的線損率計算值;s（k）為線損率實際值;m為樣本數。遺傳算法向著適應度增大的方向進行。

1.2.2 遺傳算法的實現

在Matlab 2017b的環境下，利用遺傳算法工具箱（Genetic Algorithm Toolbox，GAOT）構建GA-BP模型。

采用浮點數編碼方式：輸入層為16維，隱含層為4維，輸出層為1維，共有16×4+4×1=68個權值，4+1=5個閾值，即染色體長度為68+5=73。遺傳算法中遺傳代數取100，種群規模取50，采取算術交叉（arithXover）、輪盤賭方法。本文調用GAOT工具箱的Matlab語言：[x，endPop，bPop，trace]=gaot_ga（aa，'gabpEval'，[]，initPpp，[1e-6?1 1]，'maxGenTerm'，gen，'normGeomSelect'，0.09，'arithXover'，2，'nonUnifMutation'，[2 gen 3]），其中，目標函數定義為gabpEval。

2 仿真結果

2.1 BP模型仿真結果

在Matlab神經網絡工具箱（Neural Net Fitting）中導入訓練用的樣本集，設定好隱含層神經元個數，對數據集進行訓練。Matlab神經網絡工具箱將數據集分為訓練（Training）、驗證（Validation）、測試（Test）三部分，三者占比分別為70%，15%，15%。訓練后得到如圖4所示的網絡，該網絡經過15次迭代，達到了最小梯度的要求，為防止過擬合狀態，在驗證樣本數據的均方差連續6次未下降的情況下，達到神經網絡工具箱默認檢查值，停止訓練，在第9次迭代時取得了最佳效果。

將測試數據集（17×6）導入訓練好的神經網絡模型，經神經網絡計算得到線損率，通過Matlab繪制出計算值與實際值的對比圖以及擬合圖，如圖5、圖6所示。測試樣本的擬合值為0.947 62，BP模型計算的擬合性有待進一步提升。

2.2 GA-BP模型仿真結果

采用遺傳算法對BP模型優化后，最優個體適應度值變化如圖7所示。在進化到92代時，得到最優個體適應度值為0.000 300 138 645 377 362，滿足條件終止遺傳，得到最優權值和閾值的初始值后神經網絡開始訓練。如圖8所示，該網絡經過10次迭代，在第10次迭代時達到了最小梯度的要求，取得了最佳效果。此時訓練樣本的迭代梯度值和均方誤差均較小，分別為4.35×10-20和1.35×10-9。

將測試數據（17×6）導入訓練好的GA-BP神經網絡，通過Matlab繪制出計算值與實際值的對比圖以及擬合圖，如圖9、圖10所示，計算值和真實值之間的重合度很高，測試樣本的擬合值達到0.999 28，與單一BP模型相比（圖5、圖6），擬合度增加了5.166%。

3 仿真結果對比

將BP模型和GA-BP模型的計算值導出后與真實線損率對比，其結果見表1所列，BP模型絕對誤差最大值為0.751%，相對誤差最大值為0.127 5%。而GA-BP模型所有計算數據的絕對誤差最大值為0.14%，相對誤差最大值為0.020 4%，與單一BP模型相比，GA-BP模型的平均絕對誤差減少了0.273%，平均相對誤差減少了0.048%。

將BP模型與GA-BP模型的結果進行對比，可以發現，遺傳算法優化后的神經網絡計算精度大大提高，可完全滿足電力企業實際運行過程中計算精度的要求。

4 討 論

利用神經網絡進行線損計算目前多停留于研究階段，實際應用較少，其原因在于神經網絡需要從大量歷史數據中學習，而對于龐大的配電網而言，數據的采集和整理工作愈加困難[6]。但隨著電網技術和計算機技術的發展，智能電網和大數據是未來的發展趨勢，數據量越大越有利于模型的建立，使建立的模型更加精確。與傳統線損率計算方式相比，基于遺傳算法優化神經網絡的線損率計算模型有其獨特的優勢[7]：

（1）神經網絡模型具有強大的容錯性和魯棒性，可以避免數據采集過程中人為因素導致的數據誤差對計算精度的影響，在負荷波動較大等特殊情況下也能做到精確計算;

（2）神經網絡強大的泛化能力可以讓一個模型適應于多種應用場景，比如由于每年的用電負荷有著類似的年負荷曲線，對于同一配電線而言，通過同期月線損率數據得到的模型可以用來計算同期日線損率或者同期年線損率的值，本文用月線損率數據做訓練，用日線損率數據做測試;

（3）遺傳算法的全局尋優避免了BP神經網絡陷入局部最優的問題，最優的權值和閾值初始值可以使得BP算法更快地收斂到目標精確度，同時提高神經網絡模型的擬合效果和計算精度。

5 結 語

精確地計算線損率是電力企業綠色發展需要解決的關鍵問題，本文基于神經網絡構建了智能配電網理論線損率計算的BP模型，然后利用遺傳算法對神經網絡的初始權值閾值進行了優化，構建了GA-BP模型。對比結果表明，相較于單一BP網絡模型，GA-BP模型的計算值和實際值更加逼近，能夠更加精確地計算智能配電網的線損率。

參 考 文 獻

[1]鄭芳.河北南部電網網損分析系統的設計與實現[D].北京：北京郵電大學，2008.

[2]劉曉芳.豐鎮地區配網理論線損計算及降損策略研究[D].天津：天津大學，2017.

[3]程亮.考慮諧波電流的配電網網損計算[C]// 第九屆電能質量研討會論文集.北京：全國電壓電流等級和頻率標準化技術委員會秘書處，2018：11.

[4]馮天瑞.考慮聚類特性的中壓配網線損核心指標體系及線損模型研究[D].廣州：華南理工大學，2016.

[5]喬朋利.基于潮流計算的電力網損計算法[C]// 山東電機工程學會第五屆供電專業學術交流會論文集.濟南：山東電機工程學會，2008：7.

[6]劉社民，李建功，裴付中，等.基于改進神經網絡算法的電力系統經濟調度[J].吉林大學學報（信息科學版），2019（1）：80-87.

[7]唐曉勇.配電網線損計算方法研究[D].長沙：湖南大學，2014.

[8]劉申玉.BP神經網絡算法在配網線損計算中的應用探討[J].硅谷，2013，6（11）：114.

[9]倪洋.基于BP神經網絡的配網線損計算分析[D].大連：大連理工大學，2018.

[10]張貴暢.配電網線損分析和降損策略的研究[D].蘭州：蘭州理工大學，2018.

[11]劉麗平，張東霞，孫云超，等.基于智能算法的10 kV配電網線損評估[J].供用電，2018，35（7）：43-48.

[12]魏良良，丁祥，蔡甜，等.基于BP神經網絡與改進遺傳算法的泵站優化調度[J].水電能源科學，2019，37（5）：168-171.

[13]吳海洋，繆巍巍，郭波，等.基于遺傳算法的BP神經網絡蓄電池壽命預測研究[J].計算機與數字工程，2019，47（5）：1275-1278.

[14]楊客.遺傳算法優化的BP神經網絡在連云港港口吞吐量預測中的應用研究[D].深圳：深圳大學，2017.

[15]劉亞麗，李英娜，李川.基于遺傳算法優化BP神經網絡的線損計算研究[J].計算機應用與軟件，2019，36（3）：72-75.

[16]孫海峰，沈穎，王亞楠.基于遺傳算法優化BP神經網絡的接觸電阻預測[J].電測與儀表，2019，56（5）：77-83.