基于全局不相關的多流形學習

彭永康，李 波

(1.武漢科技大學 計算機科學與技術學院，湖北 武漢 430065；2.武漢科技大學智能信息處理與實時工業系統湖北省重點實驗室，湖北 武漢 430065)

0 引 言

在人臉識別[1]任務中，特征提取是其中非常關鍵的一環，主要的目的是為了降維，提取出關鍵的特征信息。在過去幾十年中，很多針對高維數據降維的算法被相繼提出，維數約減算法可分為線性方法和非線性方法兩類[2]。典型的線性方法有無監督的主成分分析(principal component analysis，PCA)和有監督的線性判別分析(linear discriminant analytics，LDA)[3]。代表性的非線性算法如流形學習，有拉普拉斯特征映射[4](laplacian eigenmaps，LE)算法，但是LE算法在泛化能力上表現不是很好，換句話說，測試數據使用訓練數據得到的投影矩陣計算其低維空間映射時是不容易得到的，這個問題也叫作out-of-sample問題。針對這個問題，張量化[5]、核化[6]、線性化[7]等技術相繼出現來處理這個問題。相對于LE算法，局部保持投影[8](locally preserving projections，LPP)算法計算成本低并且在聚類能力上表現良好。但是以上的LPP算法和LE算法都是基于樣本的局部結構而沒有考慮樣本的非局部結構信息，之后Yang等提出了一個非監督判別投影算法[9](unsupervised discriminant projection，UDP)，不僅注意了樣本的局部結構信息，還將樣本的非局部結構信息考慮進去。

以上的流形學習算法是基于點到點之間的距離，有以下缺陷，其一，使用點到點之間的距離學習樣本點的幾何結構信息有限，其二，抗干擾能力不強，容易受到噪聲的干擾。針對以上問題，近鄰線性組合的方法包括近鄰特征線[10](nearest feature line，NFL)和近鄰特征場[11](nearest feature plane，NFP)相繼被提出。點到特征線的距離和點到特征空間的距離相較于點到點之間的距離，可以挖掘出更多的判別信息，加強算法的判別能力。但是基于點到特征空間的距離依然容易受到噪聲的干擾，無法充分學習樣本點的局部判別信息。為了解決以上算法的缺陷，提出特征空間到特征空間距離，可以更好學習樣本之間的結構信息，同時提升算法的魯棒性，減少噪聲對算法判別能力的干擾。

通過特征抽取得到的判別信息很大程度上會存在一定的信息冗余，即判別特征向量是統計相關的。為了減少其冗余度，使判別特征是全局不相關的，將不相干約束應用于特征空間到特征空間距離度量學習，可以減少判別信息的相關性，提高算法的判別能力。

本文提出一個基于全局不相關的多流形學習算法(UFDML)。①使用特征空間到特征空間的距離，并使異類特征空間距離最大。②提出一個不相關約束應用于該算法之上，使得抽取的特征是全局不相關的。通過對LDA，LPP，UDP等算法的比較，本文提出的方法在ORL，Yale，AR人臉庫中的識別率是優于其它算法的。

1 點到特征空間距離

根據參考文獻[12,13]，點到特征空間的距離則可以由如下定義為

(1)

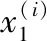
(2)

(3)

2 基于不相關的多流形學習算法

2.1 特征空間距離

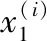
(4)

同樣的方式，樣本點xj在它的近鄰特征空間的投影點可以表示為

(5)

所以，空間到空間的距離(S2S distance)可以定義為如下所示

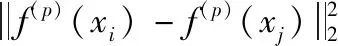
(6)

用矩陣的形式表達，則S2S距離矩陣可以表示為

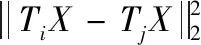
(7)

這里T是一個索引矩陣，并且矩陣的元素滿足以下的公式

(8)

2.2 特征空間多流形度量

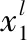
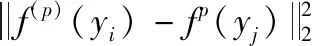
(9)

這里

(10)

這里Pij的取值為：當xi，xj屬于異類最近鄰樣本點，則記作1，否則記作0。

本算法的目的是為了找到一個最優的線性轉化，Y=WTX，通過該線性轉化可以使得異類之間的距離最大，所以尋求的投影點應是樣本點在異類特征空間的投影點，即上式可以變化成如下所示

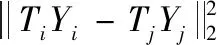
(11)

M=TTT

(12)

結合式(11)、式(12)，上式可以改寫成以下的形式

(13)

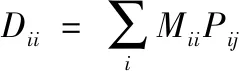
WXT(Dii-MI)XWT=WXTLXWT

(14)

這里L是一個拉普拉斯矩陣L=D-M。

2.3 不相關分析

特征抽取算法在人臉識別中扮演著非常重要的角色，但是，通過特征抽取所得到的特征往往含有重疊的判別信息，而在特征抽取算法中加入統計不相關的這個特性可以很好消除判別信息的冗余。但是很多算法往往忽視了這個性質，本文提出的算法在基于特征空間距離進行特征抽取的同時，加入了不相關約束，使得抽取的判別特征信息是統計不相關的。

由前文可得到，對于訓練樣本，判別分析可以由如下的變化得到

(15)

但是由該式得到的特征分量是統計相關的，即

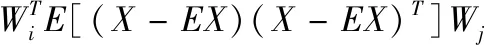
(16)

只有該等式等于0時，特征分量yi和yj是統計不相關的，但是式(15)并不能保證得到的特征分量是統計不相關，當提取出的特征分量是統計相關的，存在著冗余信息，不利于信息的提取和最終的分類。

2.4 基于全局不相關的多流形學習框架

基于以上的問題，本文提出了一個基于全局不相關的多流形學習的框架，使得異類樣本之間距離盡可能的大，樣本點經過線性轉化后得到的投影向量是全局不相關的。在式(15)的基礎上，添加一個不相關約束，使得到的判別特征是全局不相關的，并且異類樣本之間的距離盡可能的大。

提出的不相關約束要滿足抽取的特征Y=WTX，其中任意兩個特征向量yi，yj(i≠j)，是全局不相關的，這樣可以得到

(17)

這里Wi,Wj是代表矩陣W中不同的倆列，St則是代表訓練樣本的全局散度矩陣，可以表示為

(18)

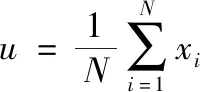
(19)

等式(17)和等式(19)整理得以下式子

WTStW=I

(20)

這里的N指訓練樣本點個數。

將該不相關約束添加到等式中，則我們最終得到的優化函數如下所示

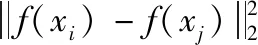
(21)

對這個優化函數進行求解，通過拉格朗日乘子法，即

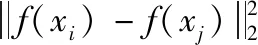
(22)

對其求偏導數，則得到以下的形式

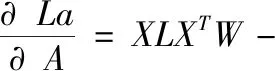
(23)

令其等于0，則得到

XLXTW=λStW

(24)

這樣，等式(24)求解可以等價于求解其廣義特征分解問題，則得到的特征向量組成的矩陣是所要求的最優化的特征轉換矩陣W。

2.5 算法流程

在上述的理論基礎上，本文提出的UFDML算法步驟見表1。

表1 基于全局不相關的多流形學習算法步驟

3 實驗和分析

為了對本文提出的方法進行驗證，將本文提出的UFDML算法與相關的經典算法進行實驗結果比較，比較的方法包括UDP，LPP，LDA算法。實驗的數據庫則選用AR，ORL，Yale這3個廣泛使用的標準人臉數據庫，以此對本文所提出算法的有效性和實用性進行評估。

3.1 數據集描述

Yale數據集中共計165張人臉圖片，分別為15個人在相似背景下的不同光照條件和表情的人臉圖片。實驗中，圖像樣本被處理成64×64的大小。

ORL數據集共計400幅灰度圖像，分別為40個人在不同時間下拍攝完成的，每個人的人臉圖像的表情變化豐富。實驗中，圖像樣本被處理成64×64的大小[14]。

AR數據集共計4000多幅圖像，分別為70名男性人臉圖像樣本和56名女性人臉圖像樣本。其中圖像的拍攝都是在不同的光照環境下拍攝完成的，表情也各不相同。

表2列出AR，ORL，Yale數據集的詳細信息。

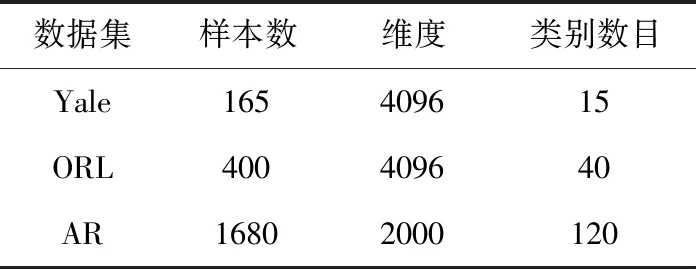
表2 AR，ORL，Yale數據集信息

3.2 AR，ORL，Yale數據集上不同方法的效果比對

在AR，ORL，Yale數據集對比實驗中，我們用本文提出的UFDML算法跟其它算法進行比較，實驗結果驗證了算法的有效性。實驗過程中，先通過各算法對原始高維數據進行降維，最后使用KNN分類器得到識別結果。

對于每個數據集，選取每個算法10次中的最高識別準確率作為最終識別結果。識別結果如下。

如表3所示，在這個實驗中，訓練樣本n隨機的選中為每類6,7,8個，并且每種算法重復訓練10次，得到每個算法最大識別率和與之對應的最佳維度。從實驗結果可以看出，本文提出的算法在訓練樣本選中6,7,8個時，得到的識別率都是優于其它3種算法的。

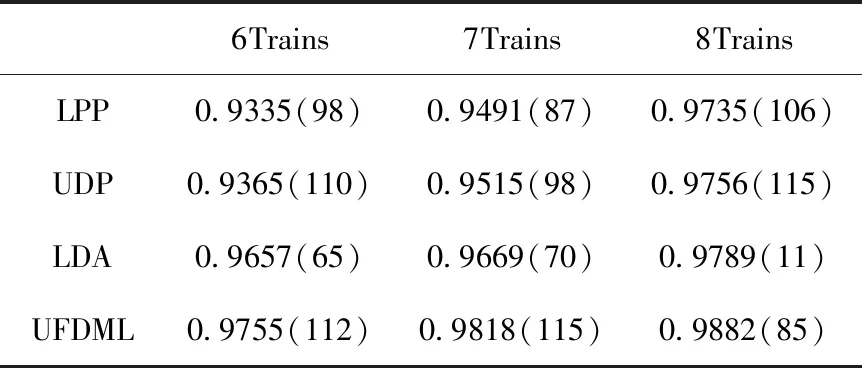
表3 UDP,LPP,UFDML,LDA在AR數據集上的識別結果

如表4所示，每一類圖像中隨機選中4,5,6個作為訓練樣本，其余的作為測試樣本，重復10次得到每個算法最大識別率和最佳維度。從實驗結果可以看出，本文提出的算法在訓練樣本選中4,5,6個時，本文提出的算法的識別能力優于其它算法。

表4 UDP,LPP,UFDML,LDA在ORL數據集上的識別結果

如表5所示，訓練樣本n隨機的選中為每類6,7,8個并重復訓練10次，得到每個算法最大識別率和對應維度。從實驗結果可以看出，本文提出的算法在訓練樣本選中6,7,8個時，得到的識別率都是優于其它3種算法的，并且實驗得到的識別率在分別劃分為6,7,8個訓練樣本時，算法的識別率是相對穩定的。

4 結束語

為了解決傳統流形學習算法中判別特征信息不夠充足，易受到噪聲影響和判別特征冗余的問題，本文提出了一種基于全局不相關的多流形學習算法(UFDML)。該算法首先通過特征空間到特征空間距離來代替傳統的點到點之間的距離，學習一個基于特征空間距離的判別矩陣，使得異類樣本點之間的距離盡可能的大，同時，加入了一個不相關的約束條件使判別特征統計不相關，最終得到最優的投影矩陣。UFDML算法有以下優點，其一，能夠更好地學習樣本點局部結構信息和抗噪聲干擾能力強，二是經過該算法抽取的特征向量是統計不相關的，這樣可以降低其冗余度，樣本點在低維空間的分類能力得到提高。在ORL，AR，Yale人臉數據庫上的實驗結果驗證了UFSDML算法的有效性和魯棒性。不足的是，與其它流形學習算法相比，本文提出的算法在計算時間上不如其它算法，因為計算投影點所造成的迭代花費時間過多，下一步的研究方向將考慮如何有效降低算法的時間復雜度。

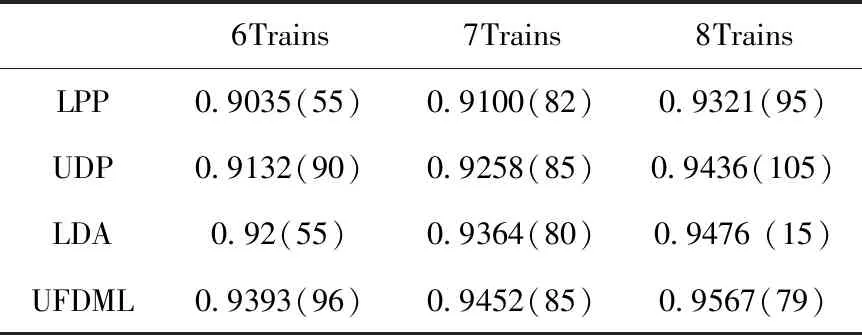
表5 UDP,LPP,UFDML,LDA在Yale數據集上的識別結果