關卡前的選擇

陳凱

源起

迷思，是一個很有意思的詞語，它的意義，遠不止于字面上的“迷惑的思考”，據說它來源于希臘語單詞Μ?θο?（mythos），是英語單詞Myth的音譯，大致是指與現實事物有所對應，能帶給人思索，但卻未必有答案的神話、傳說和虛構的故事。列維-斯特勞斯認為，人們遇到沒有辦法完全解決的矛盾時，就會編造出一些故事來作為“迷思”。似乎有這樣一種感覺，創造這些迷思，其意圖不是為那些矛盾找出解決方案，而是為了找出讓矛盾繼續存在的恰當的理由。

筆者也創造了一個虛構的故事，故事中的主角是一位探索謎之路徑的學徒，他在自己的行程中，遇見一處難以通行的關卡，為了打開關卡大門，需要解答一個謎題。但請注意，到現在為止，無論是謎題還是故事本身，它們暫時還不是“迷思”。

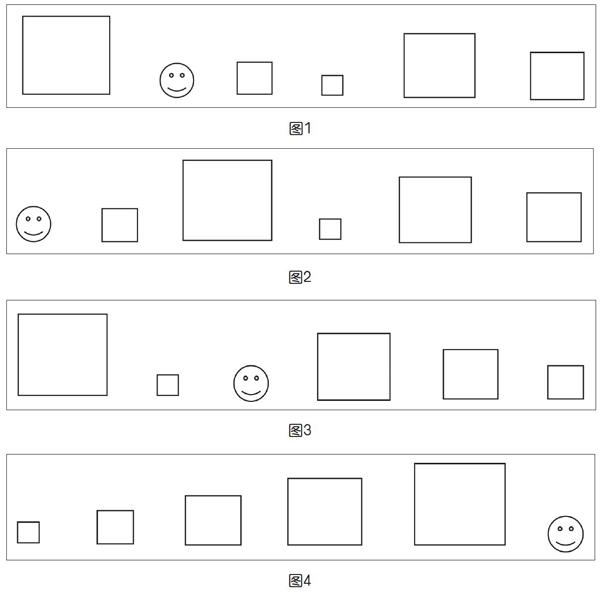
謎題是這樣的：在關卡的門前擺放著五個大小不一的箱子，必須將它們從小到大擺放整齊，門才會被打開。然而，這不是一個簡單的排序問題，因為學徒可做的動作是被嚴格限定的，他要么可以執行L動作，即交換身邊的兩個箱子，然后，再和左面的箱子換位，要么執行R動作，將自己右側的箱子扔到箱子隊列的最右面，然后再和自己右側的箱子（可能已經不是剛才在身邊的箱子了）換位。兩種動作由圖形展示出來，能更容易清楚其中的要求：初始時的狀態，如圖1所示;執行動作L后，如圖2所示;執行動作R后，如圖3所示;需要到達的最后目標可能是如圖4所示的樣子。

最后的結果，只要箱子是從小到大排列就可以了，箱子按要求排列好后，至于學徒可能會在哪個位置，可以沒有關系。當然，也可以特別規定學徒所在的位置，這會使得挑戰更具難度。大概是因為智商不夠，筆者自己在玩這個游戲的時候，沒過多久就被攪得七葷八素，對這個明明就是自己想出來的題目嘆氣。顯然，這就是人工智能應該登場的時候了。

解答

在早期的人工智能研究中，比較容易的突破點，就是各種與邏輯推理有關的智力游戲。針對上述任務，可以將各個箱子分別編碼為數字1、2、3、4、5，將人編碼為數字-1，然后存入列表。無論是L動作還是R動作，都可以很容易地用列表操作來完成。由于每次動作非L即R，所以只要在執行L或R動作之后，記錄下箱子和人位置的狀態，然后再以此狀態為基礎，繼續執行L或R狀態，可以看出，每個狀態通往新的狀態時，都面臨著一個有著兩條路徑的分叉。當某個狀態的箱子的擺放符合要求時，則可宣告解鎖完成。比起純粹隨機亂走，借助二叉樹來對左右兩個動作逐項展開比對，就不會遺漏最快的解答方法。

但要讓計算機完成任務，需要涉及不同的技能，以Python解答這個搬箱解鎖的謎題的過程為例，在數據匹配環節中需要用到二叉樹，而為了使用二叉樹，就不得不涉及更多不同的知識技能，它們之間的關系大致如圖5所示。

這張圖大致展現出：如果要借助二叉樹來解決搬箱解鎖的謎題，那么還需要很多其他知識技能的支撐，將這些支撐關系用概念圖繪制出來，可能呈現出樹狀結構，甚至更復雜一些，呈現出網狀結構，任何一個節點的缺失，都會使得任務無法達成。下面，分別對搬箱解鎖謎題解答過程中的幾段重要的Python代碼進行說明。

1.二叉樹的建立和使用

建立二叉樹的用途，是為了不遺漏所有的動作路徑，如圖6所示。

建立二叉樹的代碼如下頁圖7所示。

代碼中使用到了“anytree”庫，利用這個已封裝好的樹結構對象，可以輕松地建立起二叉樹（也可以從底層開始自行建立二叉樹對象），由于事先不可能知道二叉樹究竟可能有多深，所以無法預先給樹的每個節點命名，這里就用到了動態命名的方法：

names['x%s' % int（（i-1）/2）].name.copy（）

這句語句不僅實現了動態的樹節點命名，同時還通過取整函數，將左右兩個子節點指定給上一層的某一個父節點。

2.執行L動作和R動作

代碼中的doleft函數，作用就是執行L動作，其中涉及的都是列表操作，另外doright函數執行的是R動作，同樣是列表操作，如下頁圖8所示。

3.執行檢驗動作

檢驗函數的代碼很簡單，就是將“人”從列表中去除，然后看剩下的箱子排列是不是“12345”即可，如下頁圖9所示。

程序運行后很快就可以獲得解謎的答案，如下頁圖10所示。

同時，程序還將二叉樹列出，限于篇幅，這里只列出樹的一部分，如下頁圖11所示。

程序代碼有四十多行，并且還完全沒有考慮解題時效率上可做的優化，與許多迷題解答類的程序相比，已經算是足夠簡單了。本文中要討論的問題，不限于程序代碼及謎題解答本身。

迷思

假設學徒A和B受困于關卡之前，他們發現自己的解謎能力有限，這時，解謎大師X和Y出現了。

學徒A遇見了大師X，大師X告訴A，有許多解謎大師曾經針對不同的謎語，制造過不同的解謎法寶，自己身邊恰巧就帶著一個這樣的法寶，他稱之為搬箱解鎖函數，只要學習了函數的使用方法，便能成功解鎖，雖然稍微有些麻煩，但學徒A還是很快掌握了法寶的使用方法，他解鎖成功后，通過了關卡。

學徒B遇見了大師Y，大師Y的口袋里當然有著各種法寶，包括那個叫做搬箱解鎖函數的法寶，但它卻要求學徒自己動手，親手把那個法寶給鍛造出來。當然，這很花費時間，因為鍛造法寶的工具并不齊備，學徒需要探索通向當前大道的多條小路，去尋找到所有制造法寶的工具。問題是，工具的擁有者可能宣稱，某個工具的制作過程本身也是一個謎題——可憐的學徒于是又要去試著解開新的謎語。

學徒A和學徒B，哪一個是幸運的？正如前文所說，迷思本身沒有標準答案，或許即將出場的學生C才是最幸運的，因為他先后遇見了大師X和大師Y，也許他還遇見了大師Z，這位大師甚至沒有急著讓學徒自己打造神奇法寶，卻先是篤定地聊起那些謎題創造大師們的奇怪想法的來龍去脈，他又花了不少時間，講述那些工具鍛造師傅的手藝是怎樣練成的。

但若是存在以下兩個條件，學徒C的幸運就變成了困惑：第一，假設解開謎題通過關卡這件事本身，并不是學徒的最終任務，這一次通關僅僅是一種訓練，他的真正目標，是將來能夠自主通過各種有著奇怪謎題的關卡;第二，他和導師相處的時間是受到限制的。那么，這三位導師應該怎樣安排好和學徒C的每一次見面呢？

筆者創作這個迷思，其實就是為了映射當前基礎教育階段中人工智能教學的困難：面對某個具體的人工智能問題，如果是直接給予學習者一個封裝好的函數，那么學習者是無法體會到人工智能的具體實現過程的;但若是要講述清楚達成某個人工智能任務的各種細節，卻又受到學習者當前知識技能水平和教學時間的限制。

既然給出了迷思，筆者自己也努力嘗試著給出一種回答：大師X展現出了神奇法寶，他謎一般地通過關卡后消失了，比起關卡自身的謎題，大師X神奇法寶的由來和制造方法，則已經成了更加需要解答的謎題。大師X的行為無疑引來大師Z的一番引經據典的評述，對于大師Z云里霧里一樣的高深言論，學徒并不能一下子聽明白，這時候大師Y出場了，他找來了用以制造法寶的零件和工具，然后，他帶領著學徒，一起經歷了用這些零件和工具鍛造出神奇法寶過程中重要的一步或者幾步，有了實際的經驗，大師Z的言語或許就不那么難懂了。

雖然大師們的時間很有限，但他們不會忘記還存在著許多缺失的工具和零件，他們畫出了一幅用以進一步探索的解謎地圖。最后，他們還會囑咐道：其實，還有許多道路沒有被開拓出來，畢竟，路是人走出來的。