毫米波調頻引信的優化二維FFT信號處理算法

郭晨曦，郝新紅，栗蘋，李國林，賈瑞麗

（北京理工大學 機電工程與國家控制重點實驗室，北京100081）

毫米波調頻引信相較于傳統微波調頻引信而言，具有體積小、功耗低、質量輕、頻帶寬且分辨率高、抗干擾能力強等優點，且與激光、紅外引信相比具有全天候作戰的能力，在各國都備受重視［1］。

毫米波調頻引信的差頻信號包含了目標的距離和速度信息，目前主要有連續測距［2-3］、諧波定距［4-5］以及多普勒包絡提取［6］3類方法。連續測距類的方法主要集中在瞬時頻率估計算法研究，但是算法實時性往往無法滿足實際工程需求，工程實現有一定的難度；諧波定距與多普勒包絡提取方法需要對差頻信號進行二次混頻與濾波處理，二次混頻的參考信號頻率與調制頻率必須是嚴格的倍數關系，對數字芯片中的直接數字頻率合成器（Direct Digital Synthesizer，DDS）要求較高，而且濾波器的設計往往占用較多的系統資源，其性能的優劣將影響目標信息的提取效果。

通過分析調頻引信的差頻信號可以得到，差頻信號含有高次諧波分量且其各次諧波頻率、幅度均受到多普勒信號的調制，且還有噪聲等干擾［7］。當引信工作在毫米波段時，目標尺寸大于引信工作波長，此時調頻引信產生的差頻信號可近似看作目標多個散射點回波差頻信號的疊加，頻譜分量增多，距離信息的提取更加復雜［8-11］；實際作戰環境中，干擾機與引信為非合作目標，無法準確測量彈目相對運動速度信息，因而速度信息的提取有助于提高引信抗干擾性能。

針對毫米波調頻引信差頻信號中的距離速度信息聯合估計的問題，本文提出一種基于相對距離評價函數優化的二維快速傅里葉變換（Fast Fourier Transform，FFT）信號處理算法。首先通過分析二維FFT算法實際測距測速精度與FFT點數的關系，將選取合適點數提高精度問題等效優化問題，采用相對距離評價函數優化方法進行求解，得到FFT點數的最優解；然后對差頻信號進行采樣，將采樣得到的數據整理為二維數據矩陣形式，利用優化后的二維FFT算法對數據矩陣進行分析計算，最終提取相應的距離和速度信息；最后驗證了本文提出的算法能夠同時提高實際測距測速精度，而且優化后算法的實時性滿足毫米波調頻引信的工程需求。

1 毫米波調頻引信差頻信號模型

毫米波調頻引信的原理框圖如圖1所示。

假設引信采用三角波調制信號，此時發射信號、回波信號以及差頻信號的時頻特性如圖2所示。圖中為目標回波產生的時延，R為彈目距離，v為徑向相對速度，f為頻率，t為時間，fc為載頻，Fm為單邊頻偏，Tm為調制周期，fb，down為下掃頻段對應的差頻頻率，fb，up為上掃頻段對應的差頻頻率，c為光速。

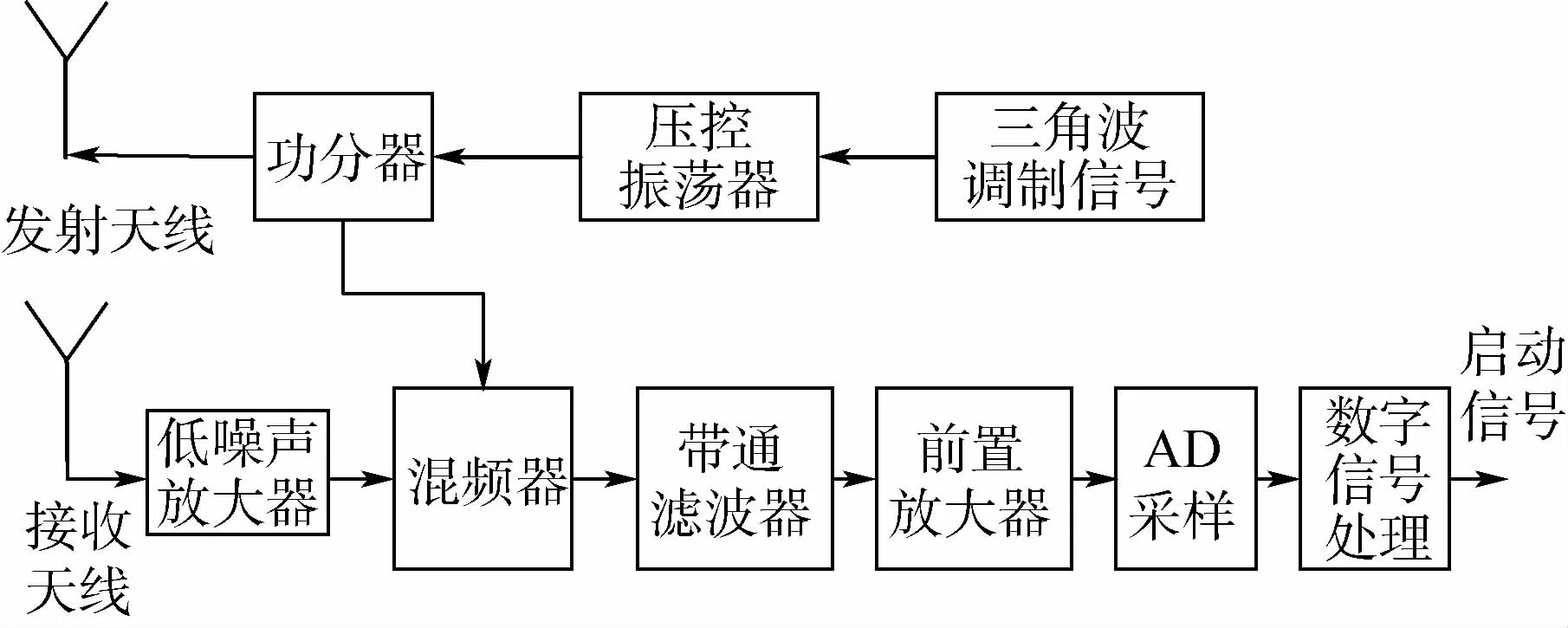
圖1 毫米波調頻引信原理框圖Fig.1 Block diagram of principle of millimeter-wave frequency modulated fuze

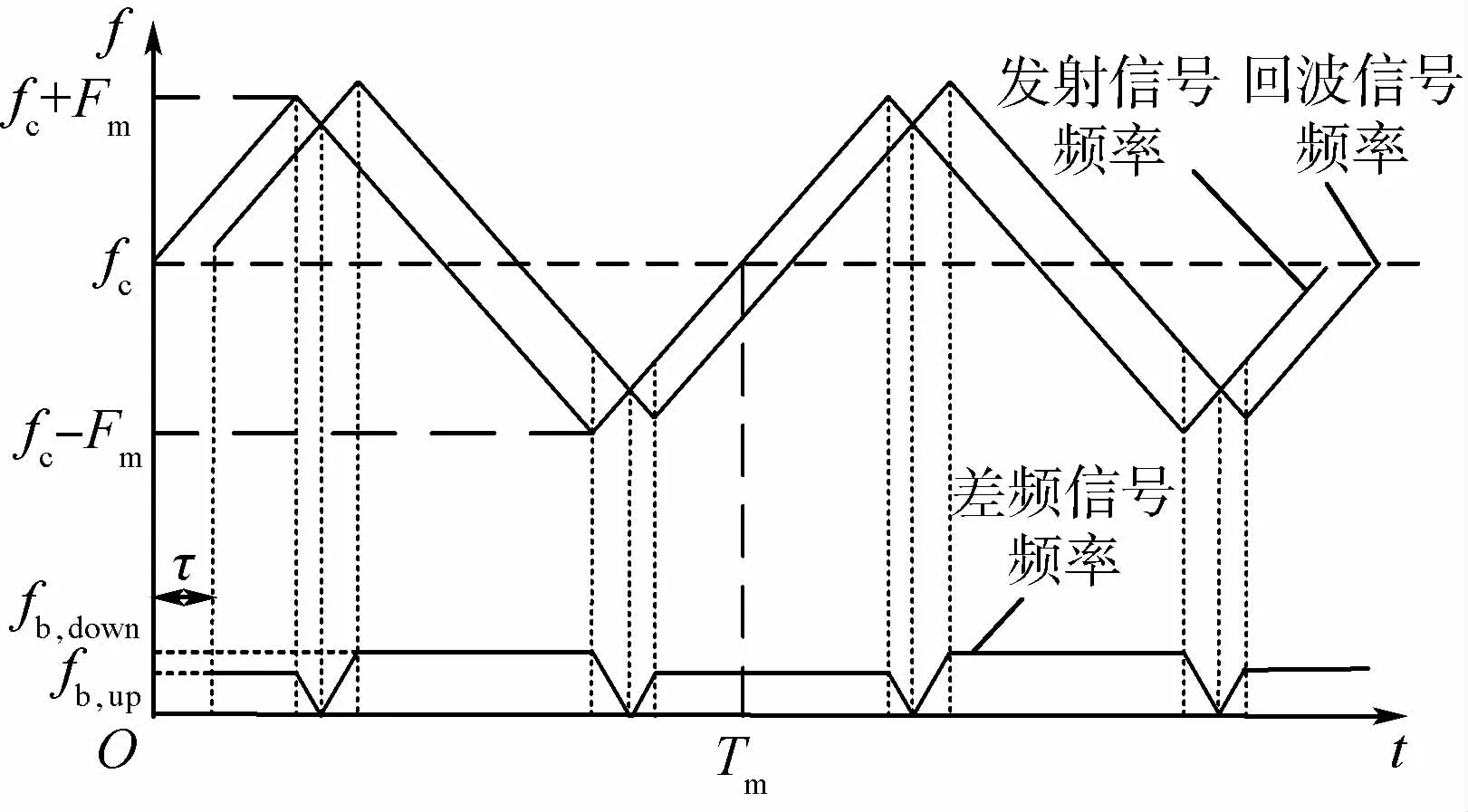
圖2 發射信號、回波信號及差頻信號時頻特性Fig.2 Time-frequency characteristics of emission signal，echo signal and beat signal

差頻信號表達式為

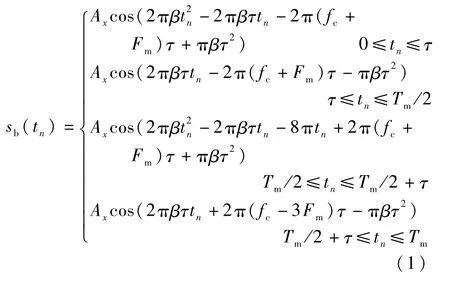
式中：Ax為差頻信號幅度為調制斜率；tn為觀測時刻。

由式（1）可知，一個周期內差頻信號由2個單頻信號和2個調頻信號組成，針對式（1）做傅里葉變換，可得一個調制周期內差頻信號頻譜為［12］

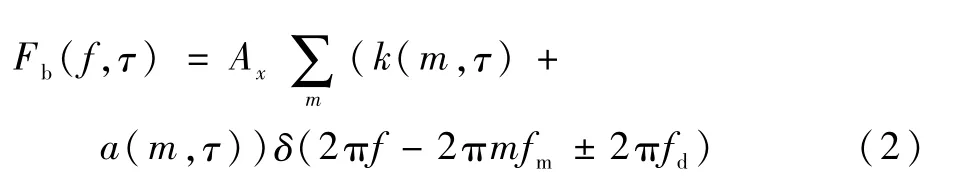
式中：k（m，τ）表示2個單頻信號的傅里葉系數；a（m，τ）表示2個調頻信號的傅里葉系數；m為諧波次數；fm為調制頻率；fd為多普勒頻率。在引信應用中，由于每個周期內2個調頻信號的持續時間很短（τ?T），它們產生的頻譜成分對后續信號處理的貢獻可忽略不計，因此，毫米波調頻引信的差頻頻譜主要考慮2個單頻信號的頻譜成分。k（m，τ）的表達式為k（m，τ）＝

式中：fc為電磁波載頻。

由式（3）可知，m次諧波出現峰值時滿足

2 基于相對距離評價函數優化的二維FFT算法

2.1 二維FFT算法原理

二維FFT是一維FFT在二維的推廣形式，現廣泛用于圖像領域的處理，處理的數據為像素矩陣［13］，其表達式為

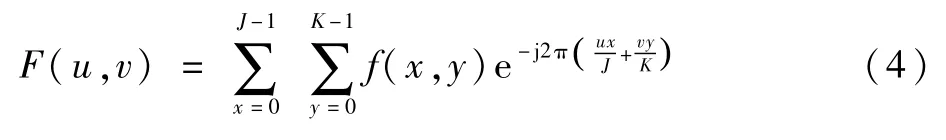
式中：f（x，y）表示要處理的二維數據矩陣，矩陣維度為J×K，x＝0，1，…，J－1，y＝0，1…，K－1；F（u，v）表示二維FFT的結果。

從式（4）中可以看出，它可以分解為2個一維FFT，即

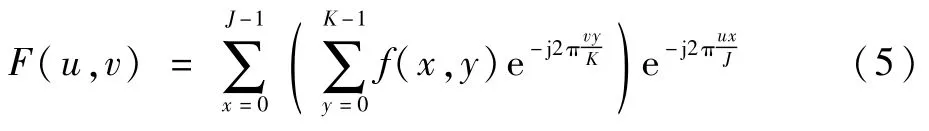
設

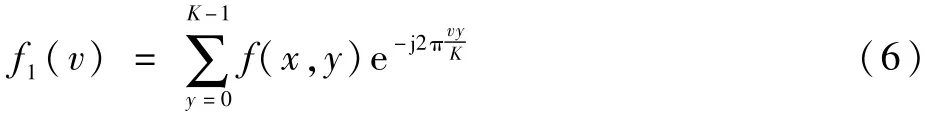
則

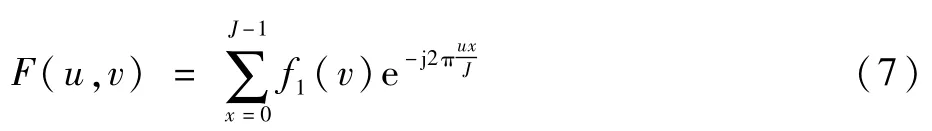
基于二維FFT算法的距離速度信息提取方法原理示意圖如圖3所示。圖3中：Amp為幅度，N為距離維FFT點數。

差頻信號首先經ADC采樣，采樣頻率為fs，將采樣后的離散信號做一次N點FFT，得到N×1的頻譜向量；積累M次N點FFT后，得到M×N的二維頻譜矩陣，再對二維矩陣按列做M點FFT，此時的采樣頻率為經過二維FFT處理后，通過峰值點檢測找到相應的頻率測量值和多普勒頻率測量值，則目標的距離與速度為

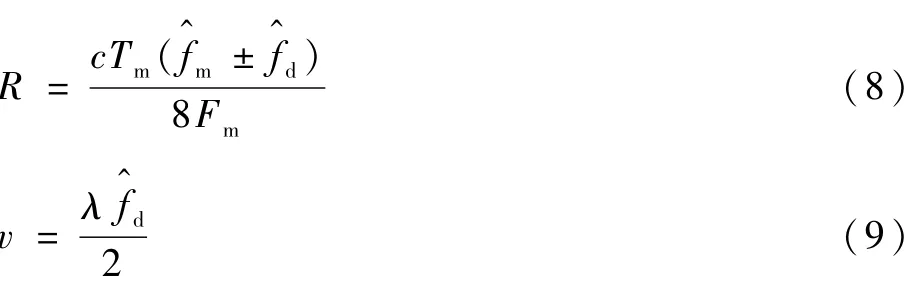
式中：λ為電磁波波長。由于所采用的三角波調制信號分上下掃頻周期，因此當找到時，應當讀取相應的采樣點數Nm，計算此時的采樣時刻，則式（8）取“＋”號；如果則式（8）取“－”號。

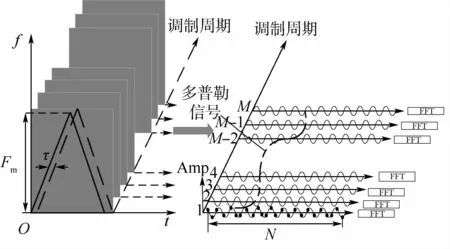
圖3 二維FFT算法提取信息方法原理示意圖Fig.3 Schematic diagram of two-dimensional FFT algorithm principle for extracting information

2.2 測距精度

由差頻信號的頻譜可知，出現峰值處的m次諧波對應的主瓣寬度為理論測距精度為與調制頻偏成反比，如圖4所示。

由圖4可知，理論測距精度隨著調制頻偏的增大而提高。然而對于調頻引信而言，由于體積和成本的限制，通過增大調制頻偏來提高理論測距精度的方法在工程上難以實現，因此當調制頻偏一定時，引信的理論測距精度為固定值，與其他因素無關。

實際測量中，測距精度與距離維FFT算法中的頻率分辨率有關，即頻率分辨率當時，多普勒頻率對測距精度影響可以忽略，此時實際測距精度Tm＝10μs，則實際測距精度與距離維FFT點數N關系如圖5所示。

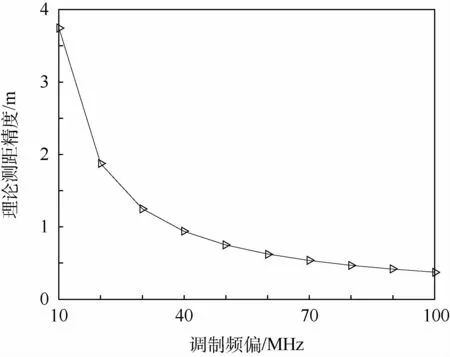
圖4 理論測距精度與調制頻偏的關系Fig.4 Relationship between theoretical ranging accuracy and modulation frequency offset

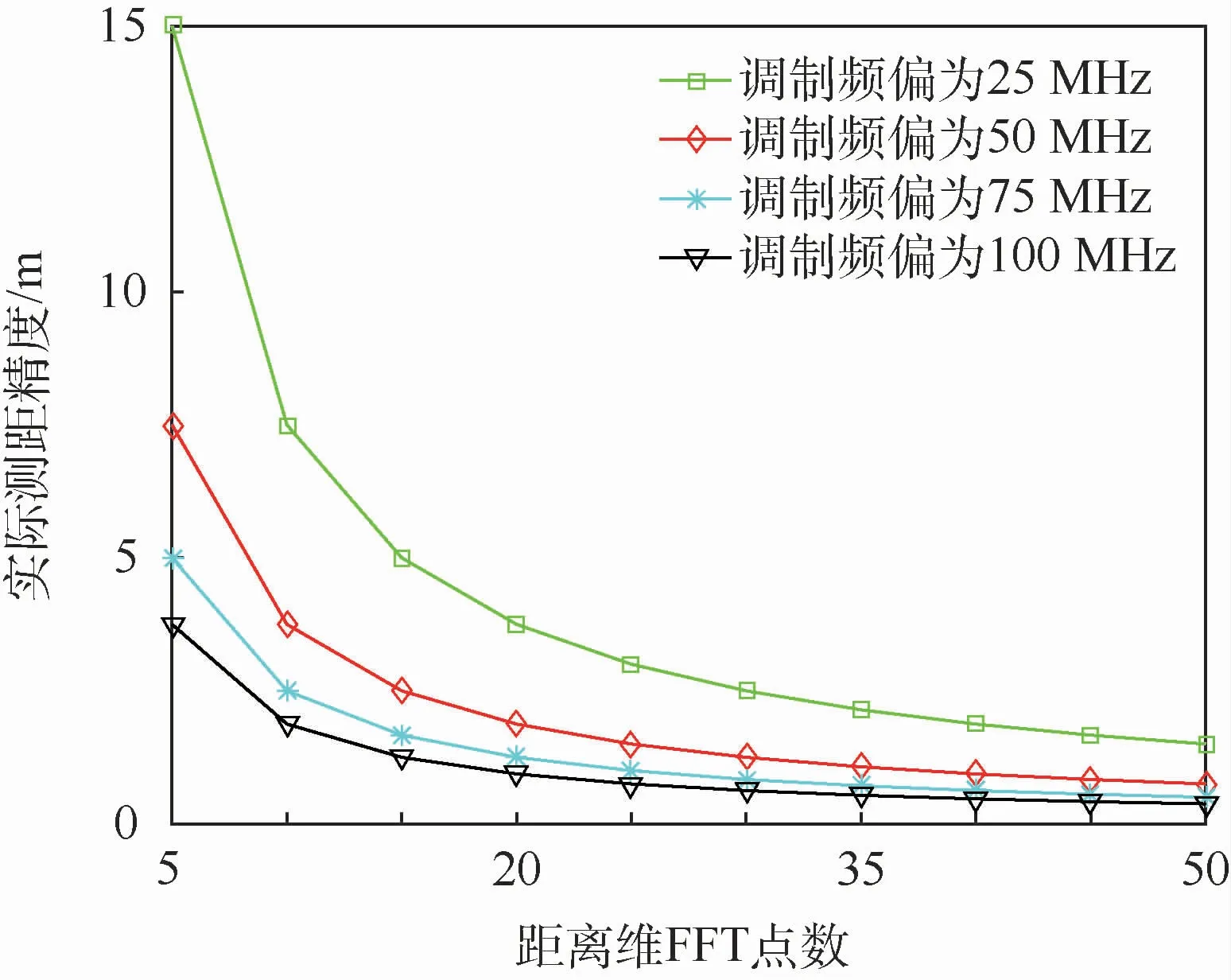
圖5 實際測距精度與距離維FFT點數的關系Fig.5 Relationship between practical ranging accuracy and distance-dimensional FFT point number

從圖5中可看出，當調制頻偏一定時，實際測距精度與距離維FFT點數成反比，當FFT點數較少時，實際測距精度較低；隨著FFT點數增加，實際測距精度提高，但是當FFT點數繼續增加時，實際測距精度變化不大，這是因為當FFT點數無限增加時，實際測距精度ΔR逐漸逼近理論測距精度ΔRT，而ΔRT與FFT點數無關，只與調制頻偏有關，因此選取合適的距離維FFT點數N對提高實際測距精度十分重要。

2.3 測速精度

由三角波線性調頻信號的模糊函數可知，信號的多普勒分辨力為則理論測速精度ΔvT＝其中L為采樣時長內調制周期的個數，如圖6所示，可以看出，隨著調制周期數L越大，理論測速精度越高。

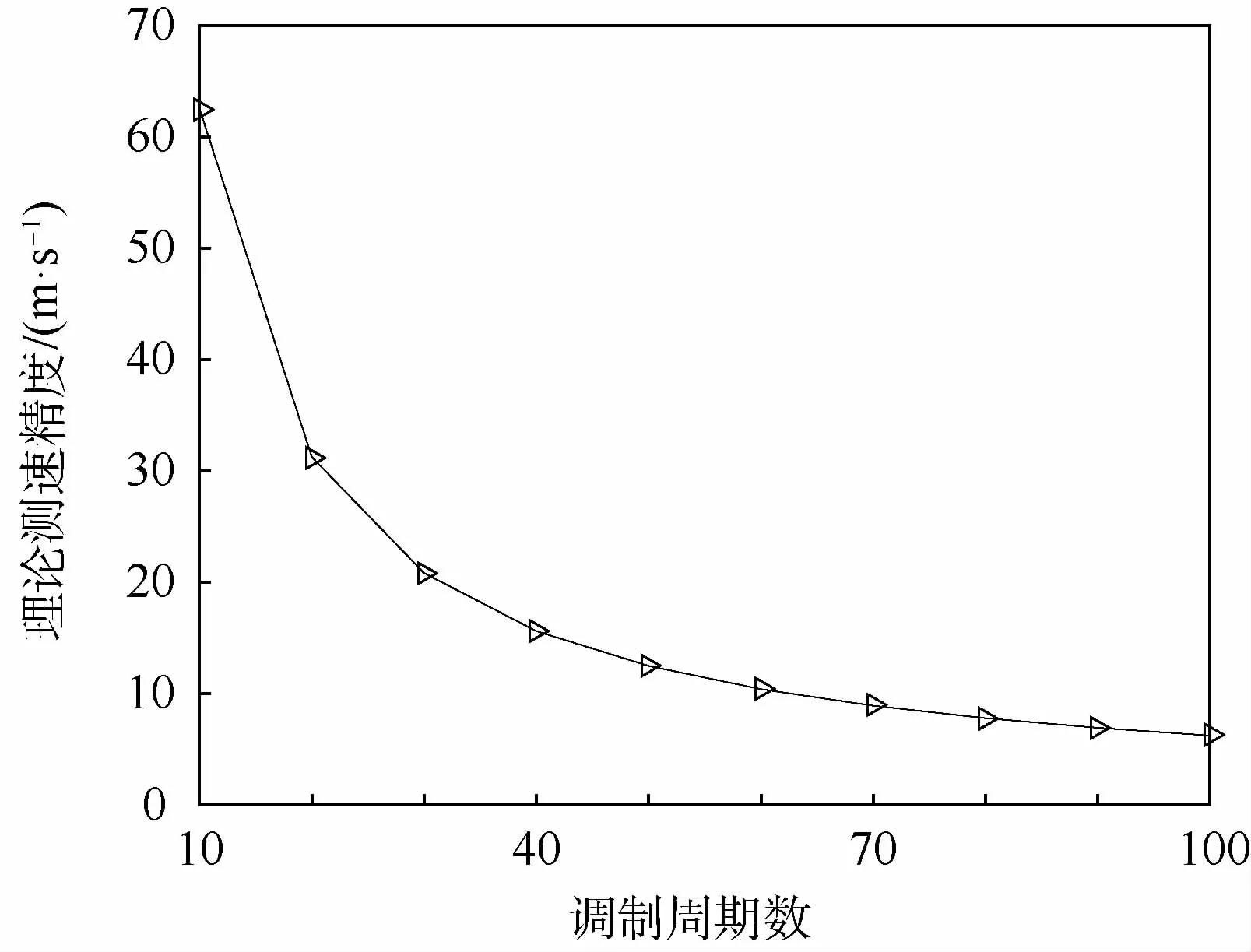
圖6 理論測速精度與調制周期數的關系Fig.6 Relationship between theoretical velocity measurement accuracy and number of modulation periods

實際測量中，由二維FFT算法對速度的提取主要是二維矩陣中的列向量FFT變換，這一過程可看作以為采樣頻率，對距離維FFT的結果進行采樣，然后做M點FFT，根據奈奎斯特采樣定理，為保證準確提取速度信息，此時的頻率分辨率實際測速精度為假設λ＝0.012 5m，fs＝5MHz，目標徑向相對運動速度v＝300m／s，則實際測速精度與距離維FFT點數N、速度維FFT點數M的關系分別如圖7、圖8所示。

由圖7和圖8可以看出，實際測速精度與距離維FFT點數N、速度維FFT點數M均成反比關系，當某一維點數一定時，隨著另一維點數的增加，實際測速精度逐漸提高，但是當點數繼續增加時，實際測速精度變化不大，且過多的點數會增加二維矩陣的維度，直接影響數據的存儲空間和計算量。實際測速精度與N、M的聯合關系如圖9所示。

圖7 實際測速精度與距離維FFT點數的關系Fig.7 Relationship between practical velocity measurement accuracy and distance-dimensional FFT point number

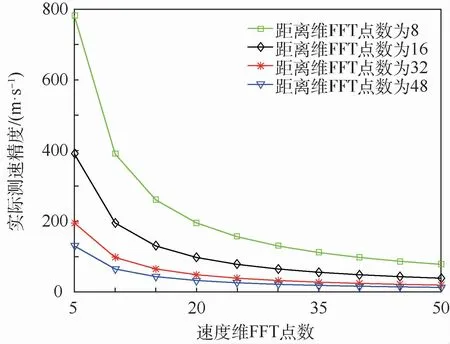
圖8 實際測速精度與速度維FFT點數的關系Fig.8 Relationship between practical velocity measurement accuracy and velocity-dimensional FFT point number

由上述分析可知，對差頻信號進行二維FFT處理時，距離維FFT點數N與速度維FFT點數M的選擇直接影響實際測距精度ΔR與實際測速精度Δv，如何選取N、M使得ΔR、Δv同時達到最優成為算法實現的關鍵問題。由ΔR、Δv表達式可知，定義則，由于k1、k2與x1、x2無關，因此優化問題中的目標函數可定義為f1（x1，x2）＝考慮如下的優化問題：

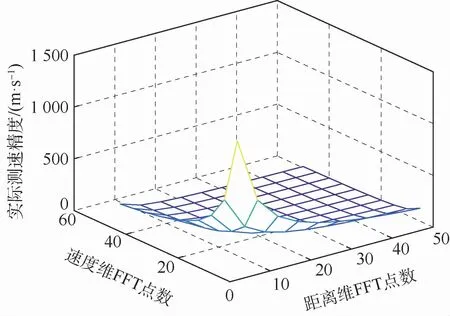
圖9 實際測速精度與距離維和速度維FFT點數的聯合關系Fig.9 Joint relationship between practical velocity measurement accuracy and distance-dimensional and velocity-dimensional FFT point number

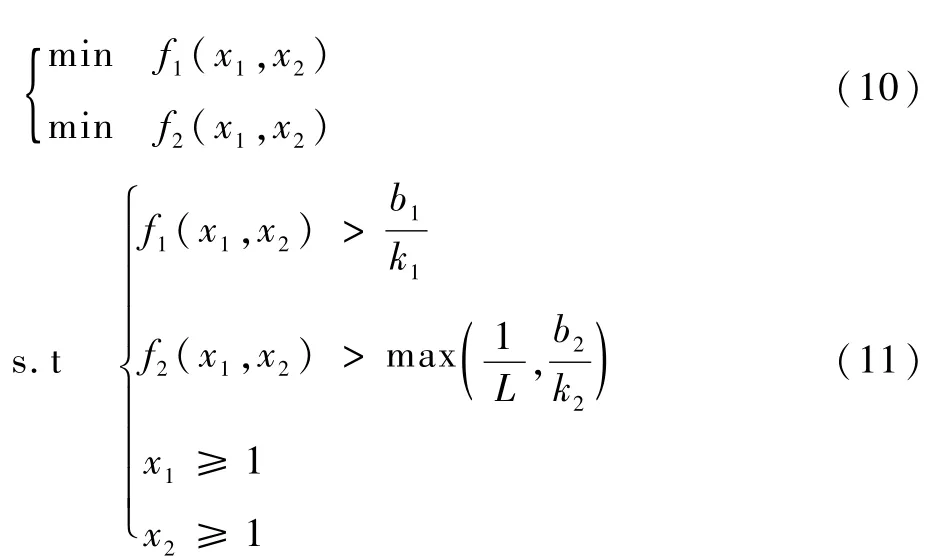
2.4 基于相對距離評價函數的優化算法

針對2.3節的優化問題，本文提出一種基于相對距離評價函數的優化算法。首先判斷約束條件（11）中的大小，然后選擇兩者中的最大值作為第2個目標函數的約束條件；其次在約束條件下求解2個單目標優化問題，即minfi（x1，x2），i＝1，2，得到2個值域最優解則為整個優化問題值域中的一個理想點，一般很難達到，于是可以構造一個基于相對距離的評價函數來尋找距離f*最近的f作為近似值，評價函數為φ（f（x1，x2））＝

然后在約束條件下求φ（f（x1，x2））的極小值，即

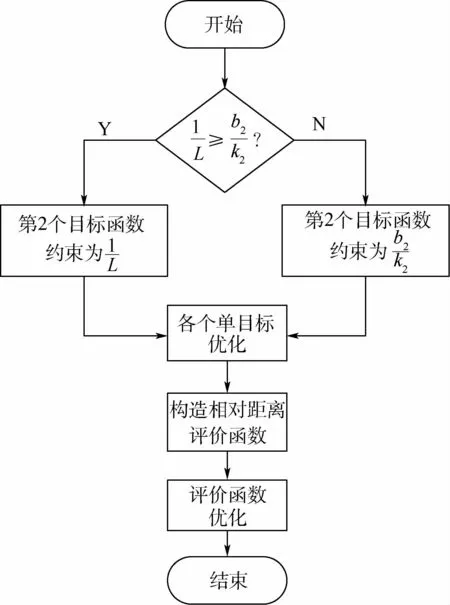
圖10 基于相對距離評價函數的優化算法流程圖Fig.10 Flowchart of optimization algorithm based on relative distance evaluation function

3 仿真與討論

3.1 優化算法的仿真討論

為驗證基于相對距離評價函數的優化算法在優化求解二維FFT點數、提高二維FFT測距測速精度方面的可行性，本文進行了蒙特卡羅實驗，實驗次數K′＝100，以實驗結果的均方根誤差（RMSE）作為評價算法的性能，表達式為

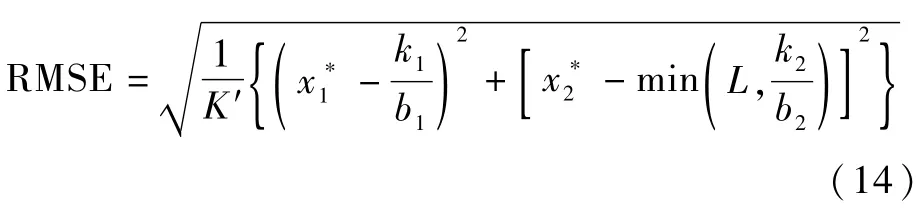
具體參數為：工作載頻fc＝24 GHz，相應的波長λ＝0.012 5m，三角波調制周期Tm＝10μs，調制頻偏Fm＝±100MHz，徑向相對運動速度為v＝300m／s，理論測距精度調制周期數，理論測速精度為b2＝ADC采樣頻率fs＝5MHz，系數從圖11中可以看出，本文算法在給定參數條件下得到一個最優解，考慮到實際二維FFT點數均為正整數，最優解為N＝49，M＝123，其對應的實際測距精度為實際測速精度為

圖12比較了傳統理想點法［14］與本文算法之間的優化性能，可以看出，隨著采樣時長內調制周期數L的增加，本文算法優化性能更好，RMSE值更接近于0，即通過最優解求出的實際測距測速精度更接近理論值。

差頻信號經過每一次N點FFT處理，信噪比的增益為10 lgN（單位：dB），因此二維FFT處理對差頻信號產生的信噪比增益為10 lg（MN）（單位：dB），關系如圖13所示。由圖中可看出，隨著點數N、M的增加，信噪比增益逐漸增大，二維FFT能有效提高差頻信號的信噪比增益。

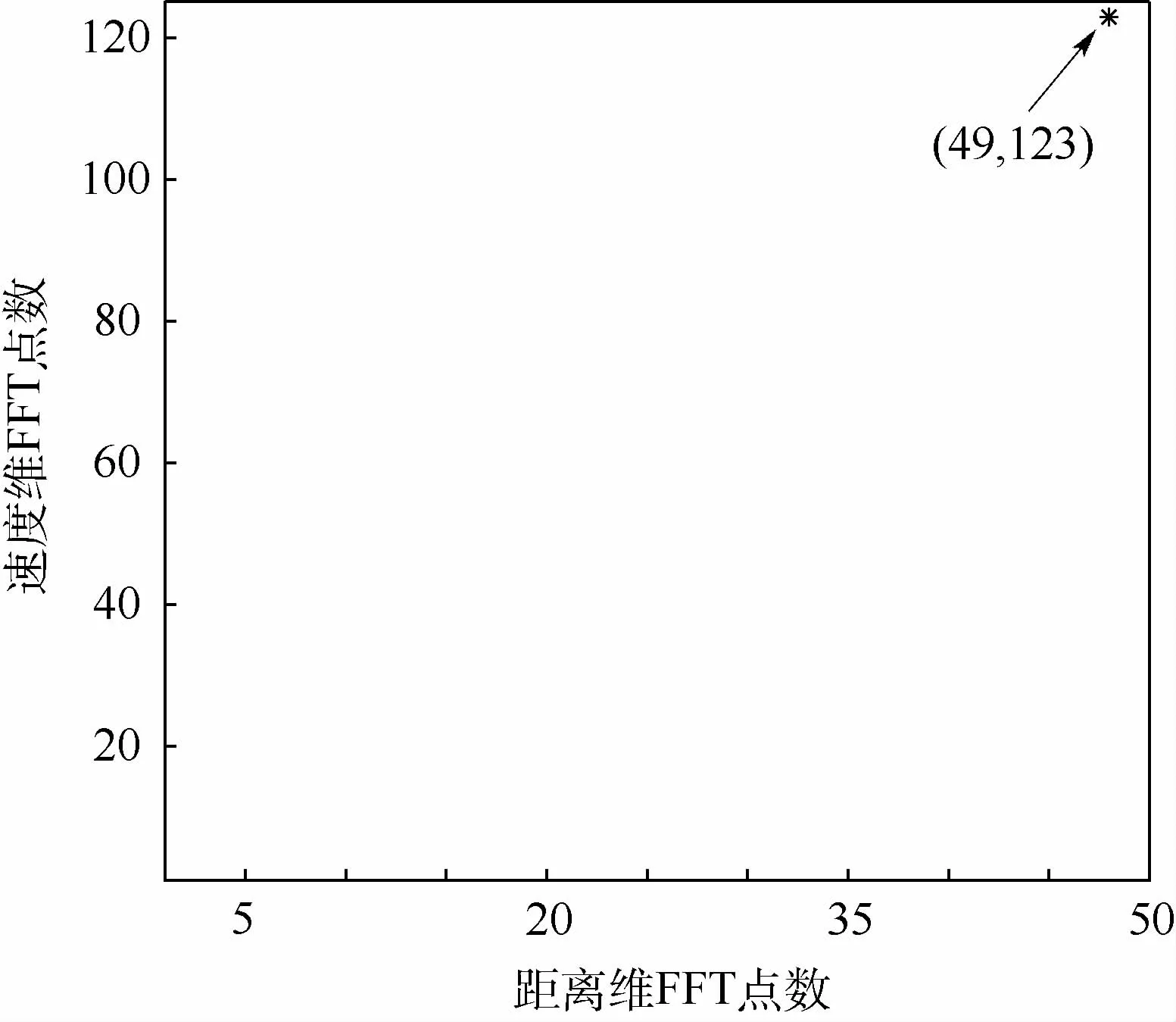
圖11 基于相對距離評價函數的最優解Fig.11 Optimal solution based on relative distance evaluation function

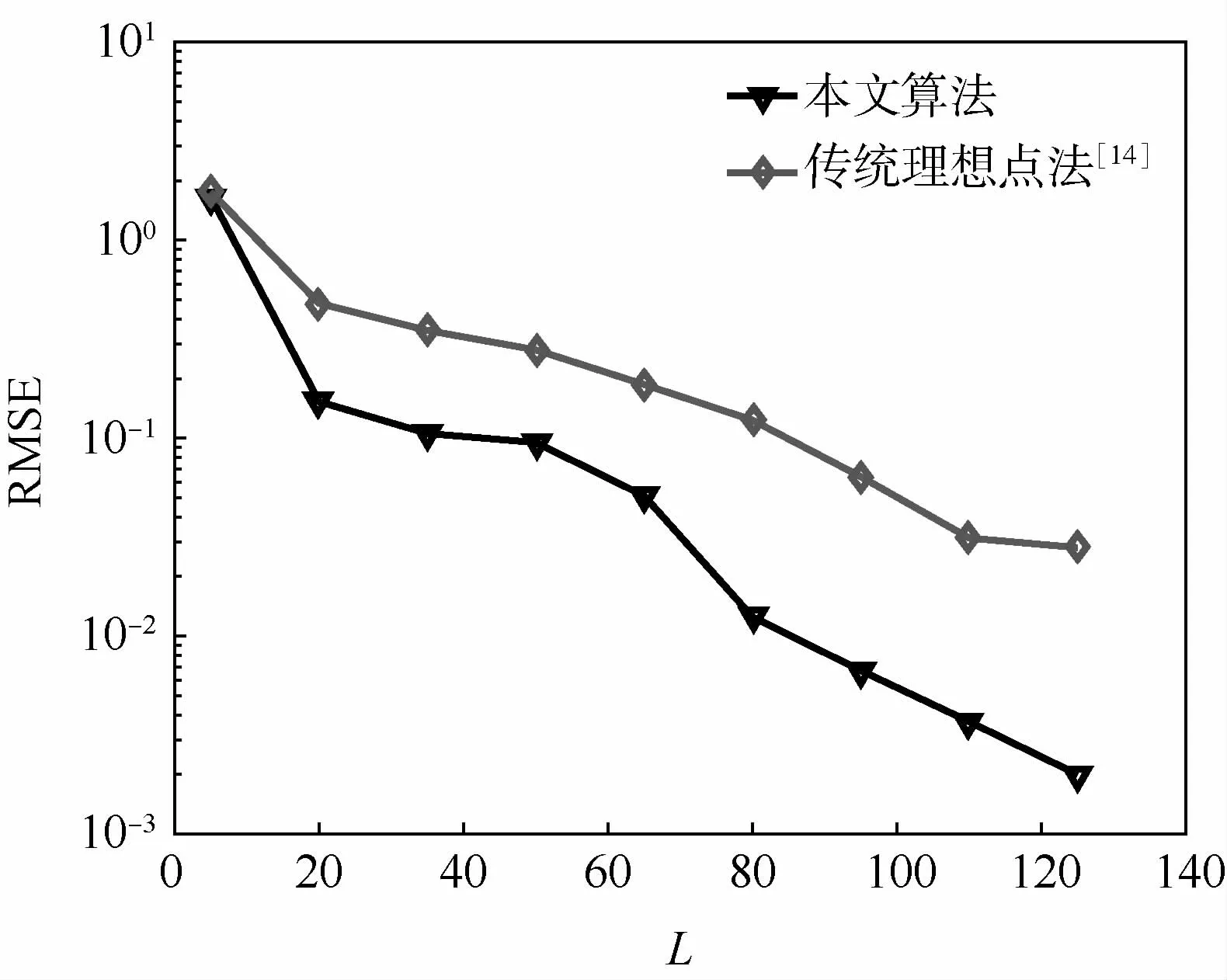
圖12 傳統理想點法與本文算法的優化性能比較Fig.12 Comparison of optimal performance between traditional ideal point method and proposed algorithm

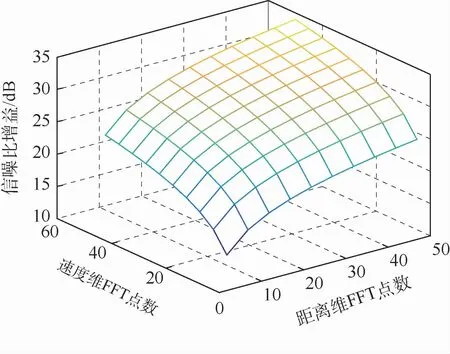
圖13 信噪比增益與距離維和速度維FFT點數的聯合關系Fig.13 Joint relationship between signal-to-noise ratio gain and distance-dimensional and velocity-dimensional FFT point number

3.2 優化后二維FFT算法仿真討論

為驗證經過優化處理后二維FFT算法估計毫米波調頻引信距離速度信息的正確性與可行性，本文將聯合采用MATLAB軟件與FPGA硬件平臺對調頻引信的差頻信號進行建模仿真。首先，使用MATLAB中的Simulink建立點目標下毫米波調頻引信差頻信號模型，如圖14所示。

具體參數與3.1節仿真參數一致，經過優化后的距離維FFT點數N＝49，速度維FFT點數M＝123，實際測距精度實際測速精度為在信噪比為10 dB的輸入下，差頻信號的時域波形如圖15所示。

將Simulink仿真產生的差頻信號送入MATLAB工作空間，對其進行二維FFT算法處理，分別得到距離維FFT頻譜圖、速度維FFT頻譜圖，如圖16、圖17所示。

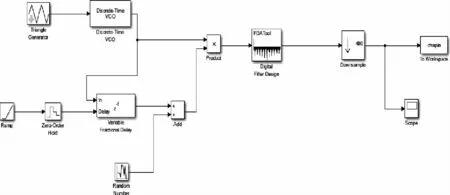
圖14 點目標下毫米波調頻引信差頻信號Simulink模型Fig.14 Simulink model of beat signal of millimeter-wave frequency modulated fuze under condition of point target

圖16中的峰值出現在8次諧波位置處（800 kHz），對應的距離為3 m，符合參數設定值；譜線間隔為102 kHz，與最優解N＝49對應的距離差頻頻率分辨率結果一致。

圖15 差頻信號的時域仿真波形Fig.15 Time domain simulation waveform of beat signal

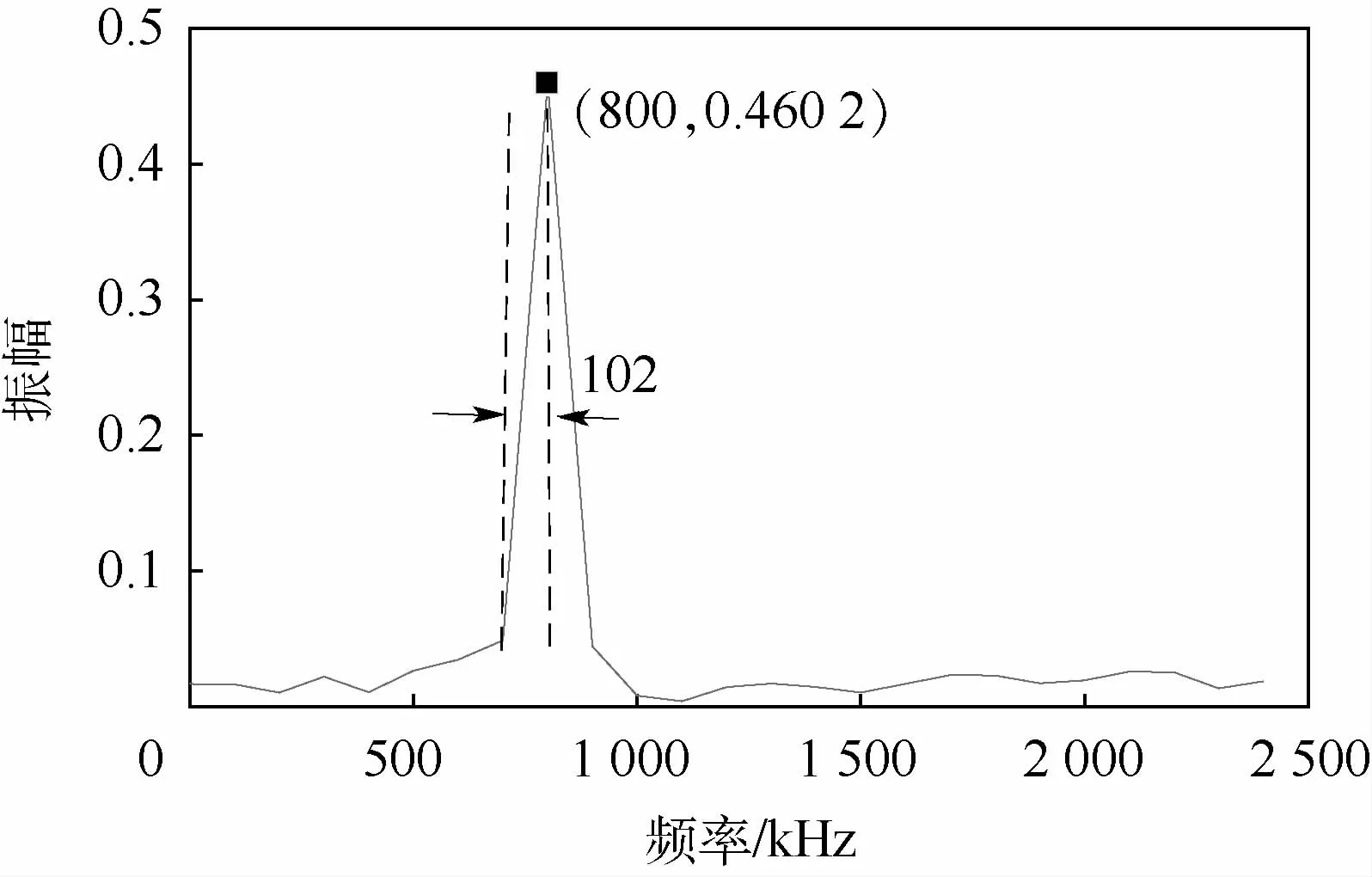
圖16 距離維FFT頻譜圖Fig.16 Range-dimensional FFT spectrogram

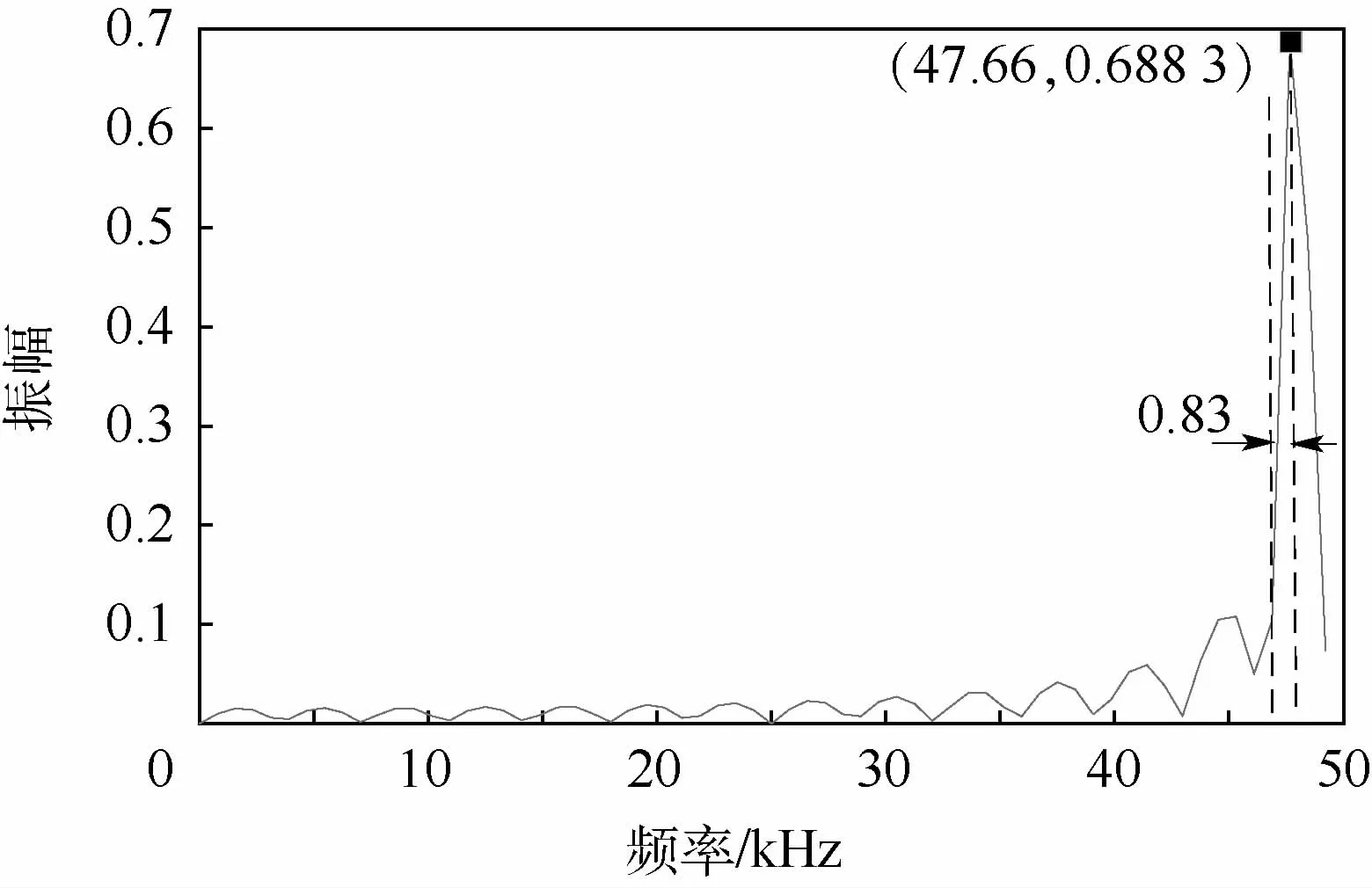
圖17 速度維FFT頻譜圖Fig.17 Velocity-dimensional FFT spectrogram

圖17中的峰值出現在位置47.66 kHz處，對應的速度為v＝297.8m／s，考慮到實際測速精度為5.18m／s，在誤差范圍內符合參數設定值；譜線間隔為0.83 kHz，與最優解N＝49，M＝123對應的多普勒頻率分辨率結果一致。

由以上仿真分析可看出，毫米波調頻引信的目標距離速度信息可以利用優化后的二維FFT算法直接提取，不用經過二次混頻和多普勒濾波即可獲得相應信息。

3.3 算法復雜度分析

優化處理算法由于在引信參數設定后可離線處理，因此不占用實時硬件處理資源；優化后的二維FFT算法復雜度主要來自于二維數據的存儲與2次FFT的計算［15］。假設二維數據存儲位數為16位，計算過程中需要存儲M組距離維N點FFT的結果和N組速度維M點FFT的結果，則存儲空間的大小為2×16×M×N；距離維FFT的復雜度為O（MNlog2N），速度維FFT的復雜度為O（NMlog2M），總 復 雜 度 為O（MNlog2N＋NMlog2M）。

表1從采樣點數、算法復雜度、測距精度和測速精度4個方面對比了優化前后二維FFT信號處理算法仿真測試結果。

從表1中可以看出，在距離分辨率和速度分辨率一定的情況下，本文提出的優化二維FFT算法能夠減少采樣點數，降低算法復雜度，適合硬件實時計算；換言之，相同采樣點數的前提下本文算法可以同時提高測距測速精度。

為了進一步驗證本文算法的實時性，采用FPGA硬件平臺進行檢驗。本文采用的FPGA芯片為Spartan 6系列中的XC6SLX16，其時鐘頻率為50MHz［16］。本文采用Verilog HDL硬件描述語言編寫二維FFT算法，整個過程中占用的資源量如圖18所示，功能仿真后的時序圖如圖19所示。

表1 優化前后仿真測試結果對比Table 1 Comparison of simulation test results before and after optimization

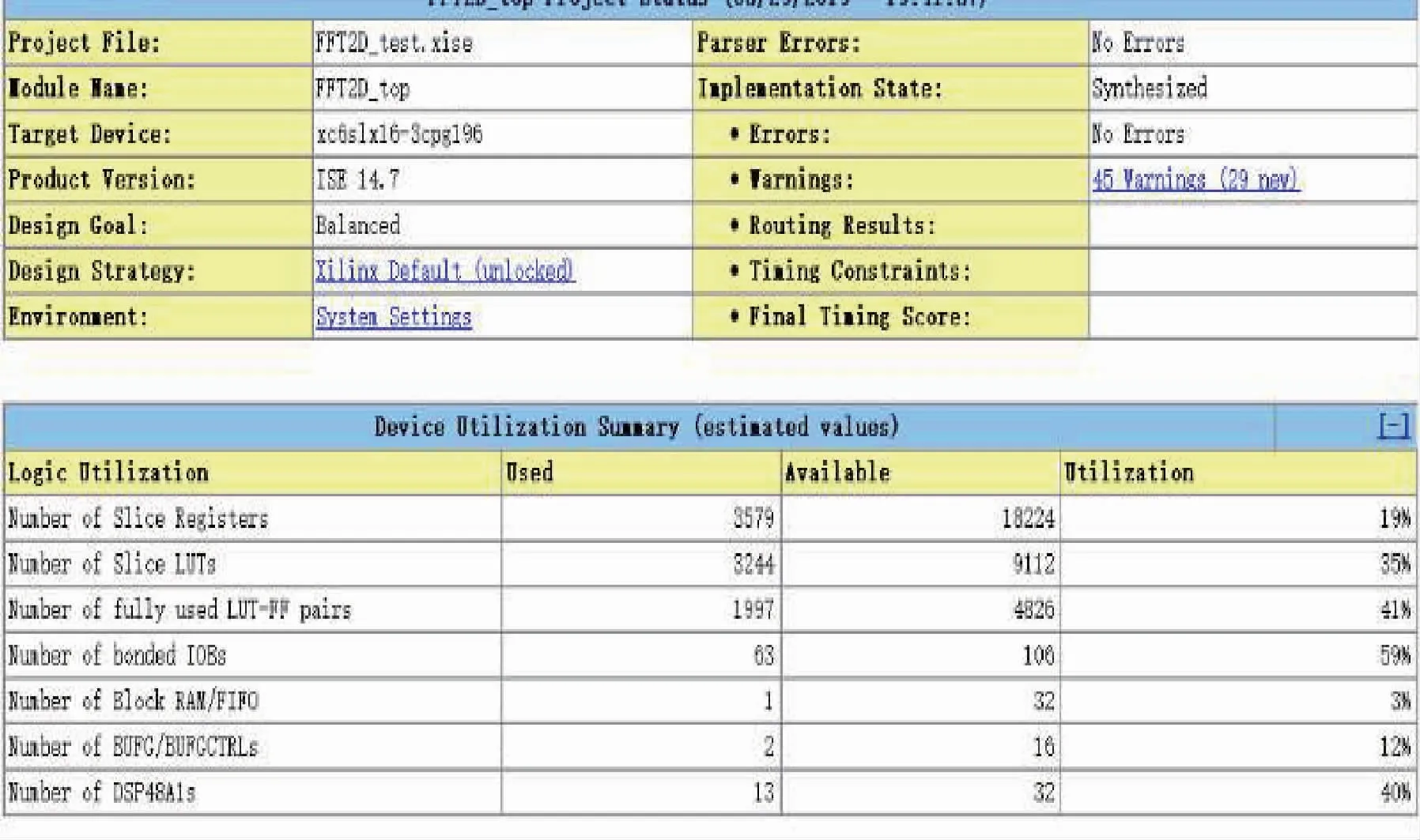
圖18 算法實現所用FPGA資源Fig.18 FPGA resource used for algorithm implementation

由圖18可以看出，本次計算使用了13個DSP48A1s單元，其中每個單元包含一個乘法器，一個加法器和一個累加器，占總量的40%；使用了一個Block RAM存儲單元，占總存儲空間的3%，滿足實際需求。

由圖19中可以看出，二維FFT算法可以在FPGA芯片上實現，其中距離維FFT頻譜峰值處對應的頻率值分別為805、903 kHz，速度維FFT頻譜峰值處對應的頻率值為49 kHz，與MATLAB仿真結果有所差異，這主要是由于數據處理過程中需要對定點數進行截位操作，從而引入一定的誤差。且每次計算時長為tatency＋MNTclk，其中Tclk為時鐘周期，tatency為距離維FFT IP核的延時，其延時與距離維FFT點數關系如表2所示。

由于采用基-2 FFT，因此距離維FFT處理時進行了補零，將49點采樣數據補零至64點數據后再做距離維FFT處理，延時latency1＝269Tclk。因此二維 FFT 算法執行一次的總時長為162.82μs，對應引信的移動距離約為0.049m，再加上采樣引起的距離延遲為則一次二維FFT處理引起的距離延遲為0.049 06 m，與實際測距精度0.383m相比很小，可忽略其對信息提取精度的影響，滿足引信實時性需求。

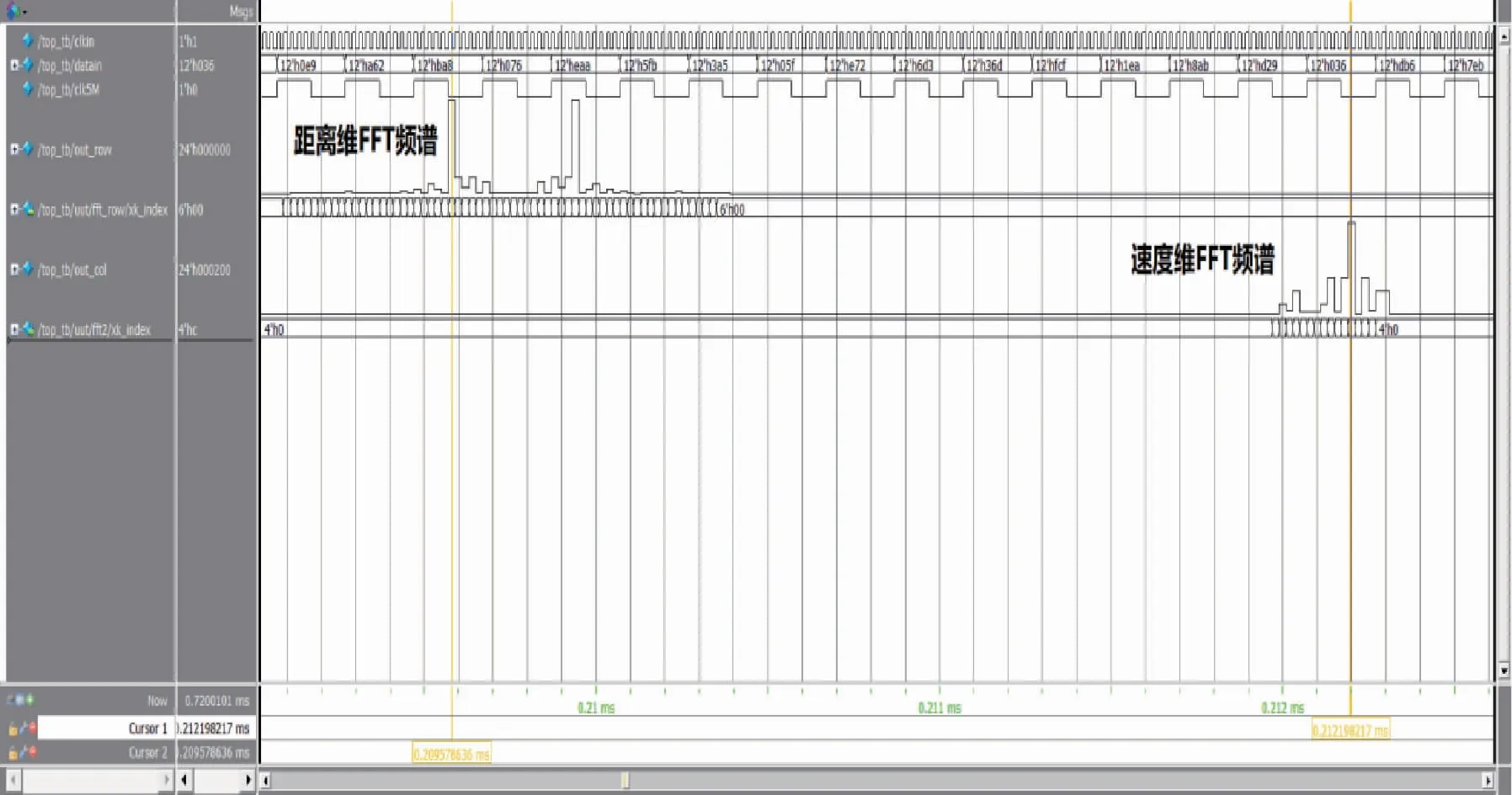
圖19 算法功能仿真時序圖Fig.19 Sequence chart of algorithm function simulation

表2 距離維FFT IP核延時與FFT點數的關系Table 2 Relationship between distance-dimensional FFT IP core delay and number of FFT points

4 結 論

1）本文通過理論分析與仿真實驗，驗證了基于相對距離評價函數優化的二維FFT算法可以用于同時提取毫米波調頻引信的距離速度信息，在實際提取過程中，需要考慮測量精度與實時性這2個因素，根據本文算法進行優化，然后再對差頻信號進行二維FFT處理，可以在測距精度與測速精度同時達到最優的條件下提取信息。

2）本文算法同時提高了實際測距測速精度，由于采用離線處理，不占用硬件資源，降低了信號處理單元中數字系統處理的復雜度。

3）本文算法的實時性滿足實際引信的工程需求，因此選用合適的FPGA芯片和外圍配置電路可以實現毫米波調頻引信的信號處理要求，能夠在復雜的環境下提取目標信息。