機場建設總進度計劃延期分布及貝葉斯估計

賈廣社，宋明禮，吳陸鋒，張普偉

（同濟大學經濟與管理學院，上海200092）

建設工程總進度計劃編制和跟蹤管理是指，在大型建設項目前期，編制一個指導整個工程設計準備、設計、采購、施工、動用前準備等方面進度的綱要型進度計劃，并定期跟蹤計劃的完成情況，提出管理建議［1］。施工進度計劃往往由施工單位編制；而總進度規劃不僅需要考慮施工進度，還需要從項目整體角度考慮其他工作進程及進度風險因素，是由建設單位或建設單位委托專門的總進度計劃管理單位進行編制和跟蹤管理，總進度計劃跟蹤管理屬于項目總控的工作范疇［1-2］。在我國近20年的機場建設工程實踐中，總進度計劃的編制與跟蹤管理顯示出重要作用，對國內14個大型機場新建、改擴建工程的進度總控咨詢成果（2000—2018年）顯示，總進度計劃管理能夠幫助建設方有效把控項目進度，滿足項目整體交付的剛性進度要求。因此，實踐中更多的機場建設項目正在引入總進度計劃管理。

總進度計劃需要符合“戰略性、總體性、宏觀性”的要求，其制訂有別于傳統的完全自下而上的進度計劃制訂方式［1，3-4］。王廣斌［1］闡述了大型建設項目總進度綱要的概念、內容、編制方法和步驟；針對大型機場航站樓建設，賈廣社等［3］通過總進度計劃實踐成果資料及訪談，確定航站樓總控工序，進而利用模擬方法估算航站樓建設總工期；羅晟等［4］通過上海世博會臨時場館項目群案例，闡釋了臨時場館項目群總進度計劃編制與控制工作的基本框架、實施要點和標準流程；祁神軍等［5］在項目總控理論基礎之上，介紹從總進度綱要直至執行性計劃的大型建設項目總進度計劃體系，并嘗試通過引入學習曲線，實現計劃的動態調整。

機場建設項目總進度計劃管理實踐中，將復雜的機場建設工程劃分為多個子系統，梳理出每個子系統工程各月度需要完成的各項具體工作；在總進度計劃跟蹤管理過程中，管理者發現當月未能按計劃完成的具體工作及其原因，制訂應對策略，預測下月進度風險情況，調整資源配置。可見，有效預測各子系統工程工作延期（即進度違約）發生數量，有利于有針對性地提前進行風險預警和資源配置，從而保障總進度計劃按期完成；也能為后續項目總進度計劃的制訂提供參考依據。隨著總進度計劃管理在機場建設工程實踐當中的應用，進度違約歷史數據得到積累，如何利用這些數據，嘗試建立統計模型反映進度風險發生規律，正是本研究所關注的問題，此類統計模型的建立能夠幫助管理者從整體角度、系統角度刻畫和理解機場建設總進度計劃實施過程中的進度違約風險。

離散分布是常見的用來刻畫風險或違約發生可能的概率模型，除了在工業制造、交通規劃、消費市場、金融信貸、保險等研究領域的廣泛應用之外，以泊松分布模型、負二項分布模型為代表的離散選擇模型也已經在工程管理領域得到了應用。Anastasopoulos等［6］運用泊松回歸和負二項回歸模型研究了高速公路建設項目索賠發生次數及其影響因素；Erskine等［7］利用負二項分布描述城市下水基礎設施的故障發生頻數，并結合貝葉斯理論建立可更新的預測模型；Love等［8］利用負二項分布擬合建設工程中工人傷亡頻數和質量缺陷發生頻數，并將二者作為建設工程項目安全和質量方面風險的被動預測指標（passive lead-indicator）。動態持續監管進度風險對提升項目績效有重要作用［9］。現階段尚缺乏對進度違約（default）頻數的研究，而工程的進度違約同安全、質量、成本等各類違約相似，都受到復雜不確定因素的影響，因而也適合用離散分布刻畫其發生頻數。所以，本文嘗試結合總進度計劃管理實踐，構建離散分布，刻畫每一個子系統一定時期內工作延期發生頻數，從項目總體和宏觀層面反映機場建設工程項目各子系統的延期風險，為總進度計劃風險預測和管理后續研究奠定基礎。

1 模型構造前提與假設

（1）重大建設工程項目有其唯一性和獨特性，但機場建設工程作為一類具有嚴格專業標準的建設工程，其進度特征如關鍵線路、延期風險等方面有一定相似性［10］。

（2）目前國內大型機場建設工程的組織管理模式，均是以指揮部為最高管理機構，下設飛行部、航站樓及衛星廳部、設備部、計財部等專項部門和職能部門來進行具體施工管理；且其工作分解結構（WBS）較為相似。相應地，建設工程子系統的劃分方法均類似于本案例，往往按照航站區、飛行區、綜合配套區等大的功能版塊，繼續細分成相應的子系統，各子系統又包括若干能夠獨立執行、監測的工作活動。以簡化的某機場建設工程為例，其子系統劃分示例如圖1所示

（3）本文假設在該組織管理模式下，當給予一定的總工期計劃目標之后，在現有管理和技術水平之下，由于受到復雜不確定因素的影響，每個跟蹤期內（本文為每月）每個子系統內發生延期工作活動數量服從一定形式的概率分布。

2 貝葉斯統計推斷與馬爾科夫蒙特卡洛（MCMC）方法

在對模型進行分布參數估計時，由于大型工程進度違約數據存在案例數量少，違約數量相對工作數量較小的特點，采用傳統參數估計方法效果并不理想，因此允許結合先驗知識并能夠實時更新的貝葉斯方法是一種較理想的估計方法；而借助MCMC方法，可以解決貝葉斯方法中的計算問題，實現分布參數的貝葉斯統計推斷。

2.1 貝葉斯統計推斷與蒙特卡洛模擬

貝葉斯分析中，一個統計模型包含：先驗分布π(θ)和似然函數L(x|θ)，其中x=(x1，x2，… ，xn)為容量為n的樣本，θ=(θ1，θ2，…，θn)為參數，樣本和參數都是隨機的。貝葉斯統計分析即是綜合先驗信息、似然（由總體和樣本信息給出），得出后驗信息。以連續分布情況為例，根據貝葉斯定理，θ的后驗分布的密度函數為

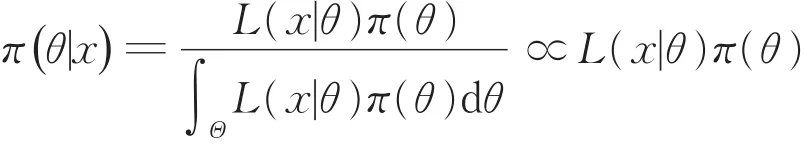
式中：π(θ)為θ的先驗密度函數；L(x|θ)為似然函數，θ∈Θ。

在平方損失函數下，參數θ的貝葉斯估計為

貝葉斯統計推斷就是要計算參數θ的后驗分布的各階矩g(θ)（如后驗均值、后驗方差等）的貝葉斯估計量，即

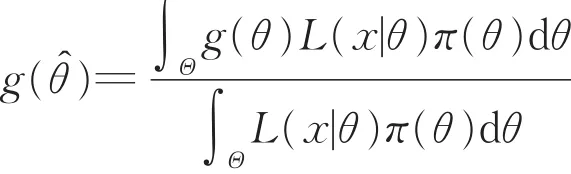
可見，要得到參數θ及其各階矩g(θ)的后驗分布，需要求以上公式中的積分，但在復雜情形或參數維數較大時，直接積分或數值積分難以實現。基于統計計算理論的抽樣方法為貝葉斯統計分析中這類復雜積分的計算提供了解決方法。可以證明，如果抽樣自后驗分布π(θ|x)的后驗樣本為獨立的，根據大數定律，樣本均值-g依概率收斂于后驗均值E[g(θ)|x]（即g(θ^)），只要樣本容量足夠大，估計精度可以達到任意所需要的精度，這就是蒙特卡洛（Monte Carlo，MC）估計。

2.2 MCMC方法簡介

蒙特卡洛隨機模擬方法能夠實現貝葉斯分析中復雜積分的運算。但當后驗分布為高維、復雜且不常見的分布時，后驗獨立樣本的抽取難度較大。馬爾科夫蒙特卡洛（Markov chain Monte Carlo，MCMC）方法便是利用馬爾科夫鏈從目標分布π(θ|x)中抽取隨機樣本，進而利用蒙特卡羅方法估算積分的方法。作為一種抽樣算法，相對于MC方法，MCMC提高了抽樣能力和效率。利用馬爾科夫鏈可將無法直接抽樣的復雜抽樣問題轉化為簡單抽樣問題。具體而言，構造一個平穩分布恰好為后驗分布π(θ|x)的馬爾科夫鏈，當馬爾科夫鏈收斂后，即該鏈上的樣本點具有了一些良好性質，如馬氏性、不可約性、遍歷性、非周期性之后，便可取該鏈上的樣本點序列作為后驗“樣本”。可以證明，這些“樣本”雖然并非相互獨立，但是卻與從π(θ|x)中直接抽取的獨立樣本具有同樣作用，可以用來以抽樣計算方法估算參數θ及其各階矩g(θ)。

3 數據來源及模型構建

本研究數據來自浦東機場三期擴建工程總進度計劃管理實踐。總進度計劃編制方法是：從子系統層面入手，結合專家經驗和宏觀規劃相關要求，通過政府相關單位訪談、建設單位及其職能部門訪談、各子系統主要承包商訪談，綜合制訂合理的、細分至子系統內各項工作活動的總進度計劃體系；在跟蹤控制過程中，研究人員全過程參與業主主持召開的各類工作會議并形成會議紀要，實時進行現場查勘獲取工程進度資料和數據，每月根據會議內容、現場資料制訂總進度月報，并進行風險預警。所截取的進度計劃跟蹤數據來自2016年7月至2018年7月，總計25個月。所選取的13個子系統（如表1所示）在該時間段內均已正式展開系統內建設工作。

各個子系統工程的進度計劃跟蹤管理表的示例如表2所示（省略部分未使用信息），該月份計劃工作活動57項，實際完成53項，發生延期4項。本文使用的數據包括月度各系統內開展工作活動的總數量，以及其中發生延期的工作數量。

表1 案例機場項目所選取的子系統Tab.1 Subsystems of the case airport construction project

對于每個子系統，構建一個離散概率分布，來刻畫一定時期內可能發生的延期活動數量（延期活動頻數）。令延期活動頻數分布表示為f(nt|θ)，其中nt表示一個子系統在第t個月發生的延期活動數量，由于所跟蹤的時間共m個月，所以t=1，2，…，m。θ表示該分布的參數，則某一子系統在m個月內發生延期活動數量的似然函數為

對于一定時間內超期活動發生若干次數的概率，適宜采用描述離散隨機事件的概率分布來進行刻畫，因此本文中選用泊松分布（Poisson distribution）和 負 二 項 分 布（negative binomial distribution）進行研究。

4 參數估計過程

4.1 極大似然方法

對于泊松分布和負二項分布假設，根據案例數據，采用極大似然估計來計算分布參數，具體采用牛頓法迭代求解似然函數。表3展示了延期發生數量概率分布參數的極大似然估計值。表中λ為泊松分布參數，θ、r為負二項分布參數。

4.2 貝葉斯方法

4.2.1 泊松分布假設

對于每一個子系統，假設其在25個月中，每個月發生的延期工作數量nt服從泊松分布，即

式中：t=1，2，…，25。

則似然函數形式為

在貝葉斯后驗分析當中，先驗分布通常選取共軛先驗分布形式，這是因為貝葉斯后驗分布既反映過往的經驗（參數的先驗分布），又反映樣本的信息（觀測數據），而共軛型分布要求先驗分布與后驗分布為同一種分布類型，所以選取共軛先驗分布就意味著使經驗知識與現有樣本信息具有某種同一性，它們能夠轉化為同一類的經驗知識；并且，所得到后驗分布作為新的經驗知識進行下一步貝葉斯信念更新后，所得到的新的后驗分布仍然是同一類型的。對于泊松分布的參數λ，取其共軛先驗分布Gamma分布作為先驗分布，即

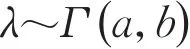
式中：a，b為超參數。

超參數可根據先驗信息確定，本研究假設總進度計劃實施受到難以預知的復雜隨機因素影響，采用提供十分有限信息的非信息（uninformative）先驗。其一，根據課題組以往參加的機場建設工程實踐記錄，在類似項目分類以及工作實施過程中，每月發生的延期工作數量不會超過10個，除此之外，缺乏其他先驗信息，由此可采用先驗分布λ～Γ(5，1)；其二，采用模糊先驗（后文將進行論述）。需要指出的是，本研究假設所選取的先驗分布，是提供了有限的、較為“模糊”的客觀信息。這兩類先驗都可稱為非信息先驗（uninformative prior），這是相對于信息先驗（informative prior）而言，非信息先驗表示對于研究對象的先驗知識十分有限。而信息先驗則是指通過實踐經驗、專家知識等形成了對于研究對象較為豐富的經驗知識。本文采用非信息先驗，旨在介紹貝葉斯統計推斷方法在延期頻數分布研究中的應用，并給出具體實現過程示例；而至于先驗信息的進一步收集、豐富和引入，則可按相應的理論和方法進行進一步研究。

表2 某月“航站樓/衛星廳工程”子系統內計劃活動及完成情況Tab.2 Planned activities and completion of subsystem“terminal/satellite hall project”in a certain month

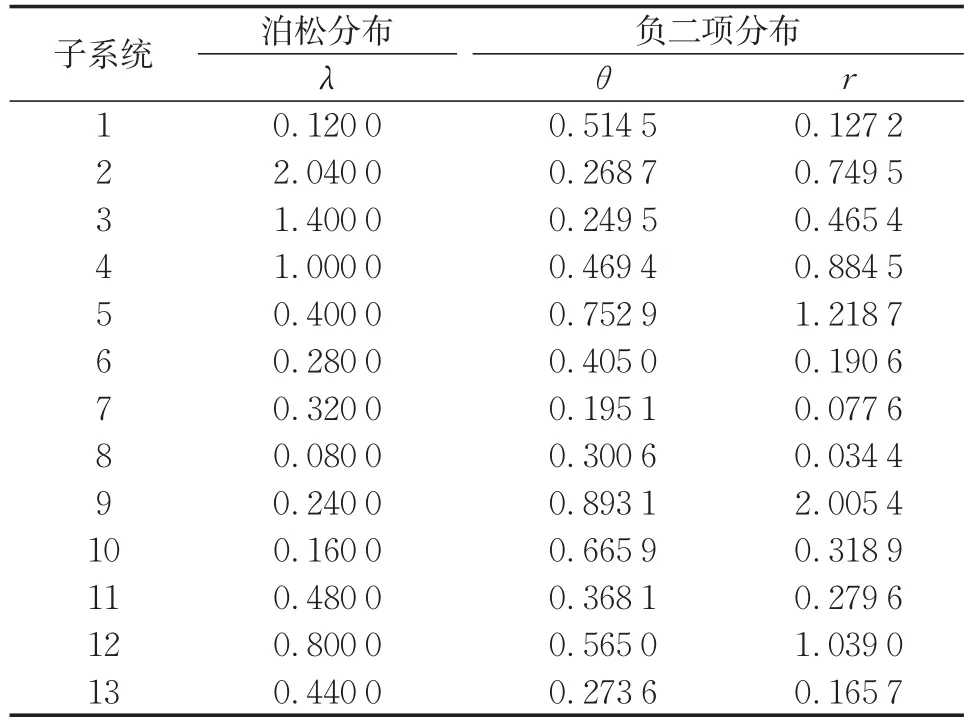
表3 頻數分布參數的極大似然估計值Tab.3 Maximum likelihood estimates of frequency distributions

先驗分布λ～Γ(5,1)的圖像如圖2所示。

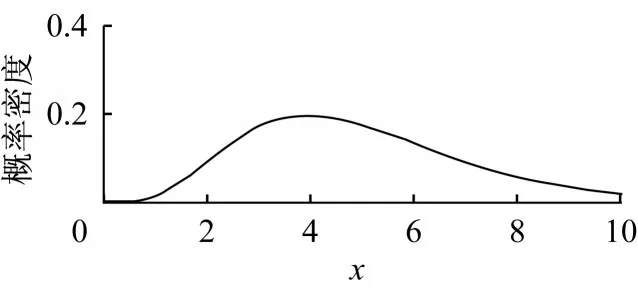
圖2 參數λ的共軛先驗分布Γ（5，1）Fig.2 Prior Γ（5，1）for parameter λ

由于所選取的是共軛先驗分布，參數λ的后驗分布也將服從Gamma分布形式，因此可以直接采用MCMC算法中的Gibbs抽樣方法進行抽樣計算，得到后驗樣本，進行后驗分析。以3號子系統“捷運系統工程”為例圖3為3號子系統泊松分布參數λ的后驗抽樣樣本路徑。可以看出，圖3中無持續扁平區域，且波動并不過分集中。

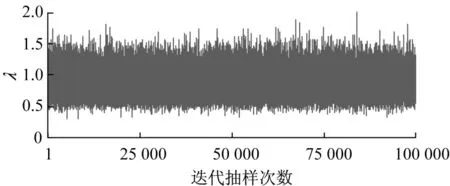
圖3 泊松分布參數的后驗抽樣樣本路徑（3號子系統）Fig.3 Parameter sample paths for Poisson distribution(Subsystem 3)

類似地，從圖4所示的后驗抽樣跡圖可見，MCMC算法模擬產生的參數值無明顯趨勢特征（tendency）或周期特征（periodicity），所產生樣本參數值絕大部分都在同一值域之內。說明抽樣確實符合馬爾科夫鏈特征，即每一狀態都與其歷史狀態相關；同時每個值隨機持續波動，符合蒙特卡洛方法獨立抽樣的需求。

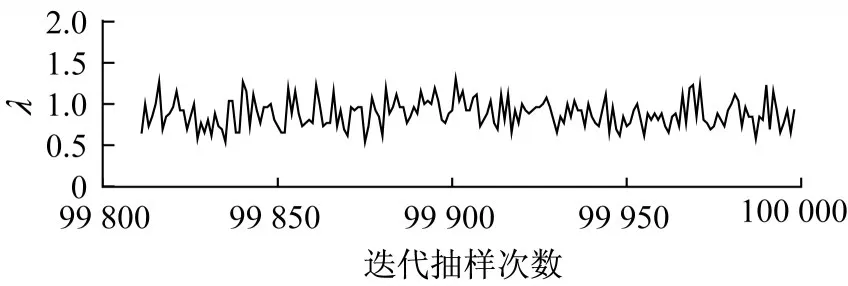
圖4 泊松分布參數的后驗抽樣跡圖（3號子系統）Fig.4 Parameter sample trace plot for Poisson distribution(Subsystem 3)

以上兩步為從不同角度進行的算法收斂性檢驗，除此之外，還可以用遍歷均值圖（ergodic mean）方法對收斂性進行檢驗。從非周期性、馬氏性、遍歷性等不同角度來判斷，此處所使用的MCMC算法皆收斂良好。針對本文選取的參數先驗分布及其超參數，該抽樣算法能夠成功地在參數取值空間隨機抽取樣本［11］，且并沒有長時間停滯在參數空間的某一個小區域進行抽樣），因此所產生的馬爾科夫鏈上的抽樣點雖然并非相互獨立，但是卻與從后驗分布中直接抽取的獨立樣本具有同樣作用，可以用來以抽樣計算方法估算參數θ。注意，這里舍棄了前20 000個樣本點，作為抽樣預熱階段（burn-in period），保留下來的樣本點是更加接近馬爾科夫鏈平穩分布的樣本點，本文據此進行后驗分布統計量的計算。泊松分布參數λ的后驗密度估計如圖5所示。

對于3號子系統“捷運系統工程”，泊松分布假設下MCMC過程產生參數樣本的自相關圖如圖6所示，其中Lag值為滯后階數，如Lag值為3時，表示該抽樣樣本與其后第3個抽樣樣本之間的自相關程度。表4則展示了在Lag值取1至49時，參數λ抽樣結果具體的自相關系數值。從圖6與表4可以看出，后驗抽樣樣本的自相關程度非常低，從判斷抽樣算法收斂的角度來看，這是一個理想結果。

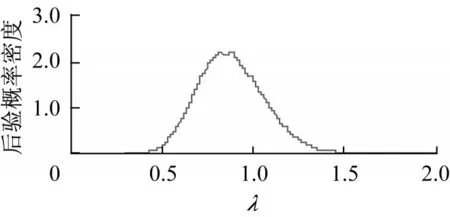
圖5 泊松分布參數的后驗密度估計圖（3號子系統，后驗抽樣樣本數為80 000）Fig.5 Parameter density plot for Poisson distribution(Subsystem 3,sample:80 000)

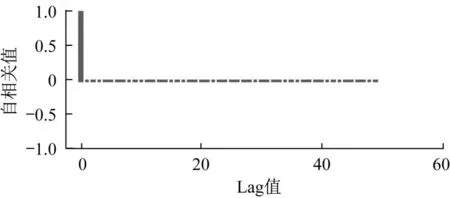
圖6 泊松分布MCMC過程的自相關圖（3號子系統）Fig.6 Autocorrelation plot for Poisson distribution(Subsystem 3)

蒙特卡洛誤差（MC error）Me是基于MCMC方法輸出結果所計算的重要指標，用于衡量模擬計算而得的參數值的變動程度。本文采用分塊均值（batch mean）計算Me值，簡而言之，就是將MCMC方法產生的所有樣本T均分為K個分塊，每個分塊含有v=T/K個樣本，先計算每個分塊的均值，對所得的所有分塊均值求標準差，即為分塊均值法計算的Me值。可見，較小的Me值意味著根據模擬樣本所計算的參數估計值變動較小，即對參數的估計具有較高的精確度［11］。并且，Me值也是監測MCMC算法收斂性地重要指標，較小的Me值是算法收斂的必要條件。

各子系統后驗抽樣過程所計算的Me值如表5所示。從表5可見，相對于后驗樣本標準差，Me值均很小，可以說明對參數的估計比較準確。

本案例中，對其他各個子系統參數進行抽樣后，以上各后驗分析過程也都能得出類似結果，證明MCMC算法收斂，且估計結果符合精度要求。

另外，如前所述，還可采用“模糊先驗”［12］（vague prior）作為先驗分布，具體來說，令Gamma分布Γ(a，b)的均值和方差分別等于先驗均值-λ和先驗方差S2λ，由于Gamma分布Γ(a，b)的均值和方差為

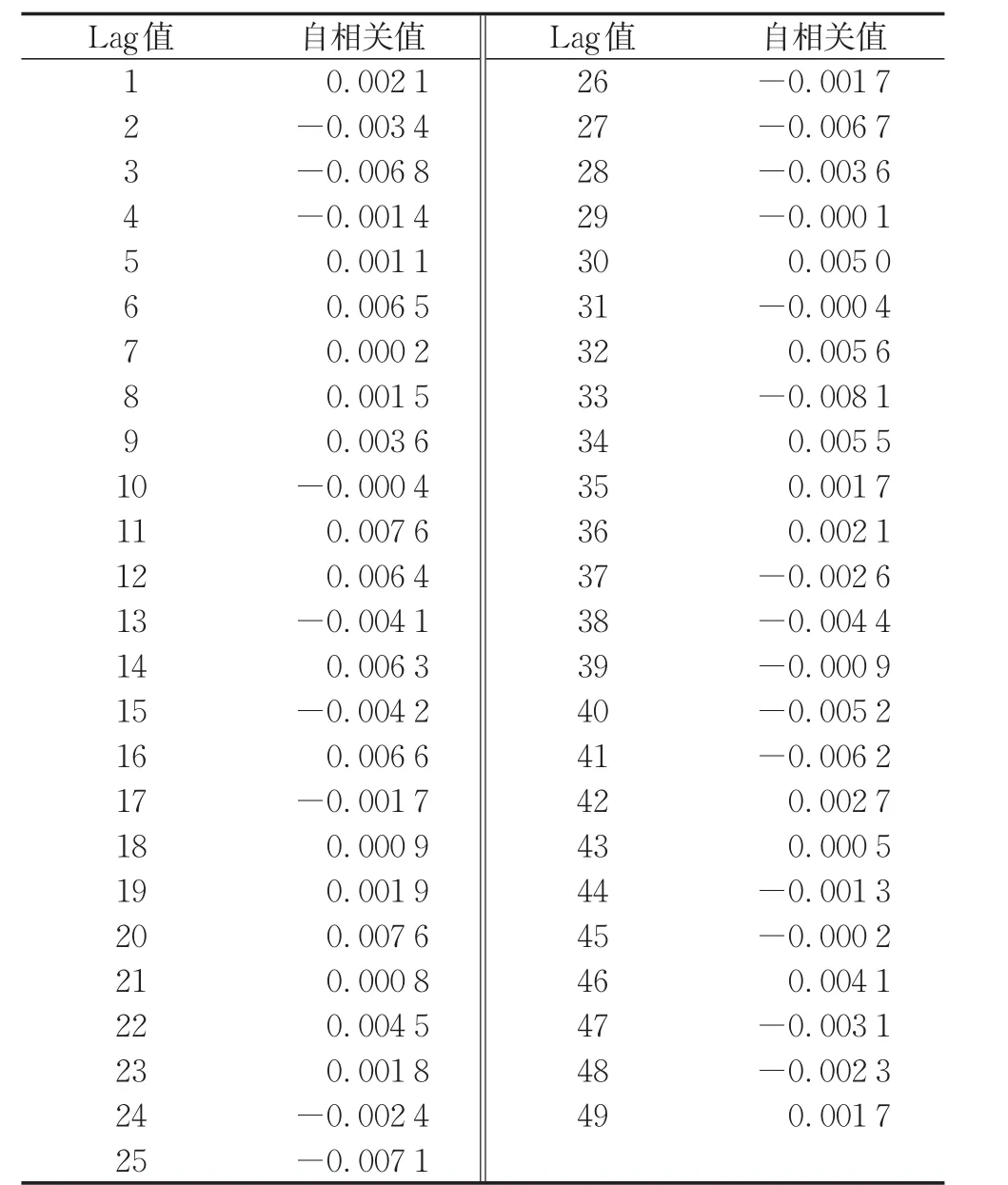
表4 泊松分布MCMC過程的自相關值（3號子系統）Tab.4 Autocorrelations for Poisson distribution(Subsystem 3)

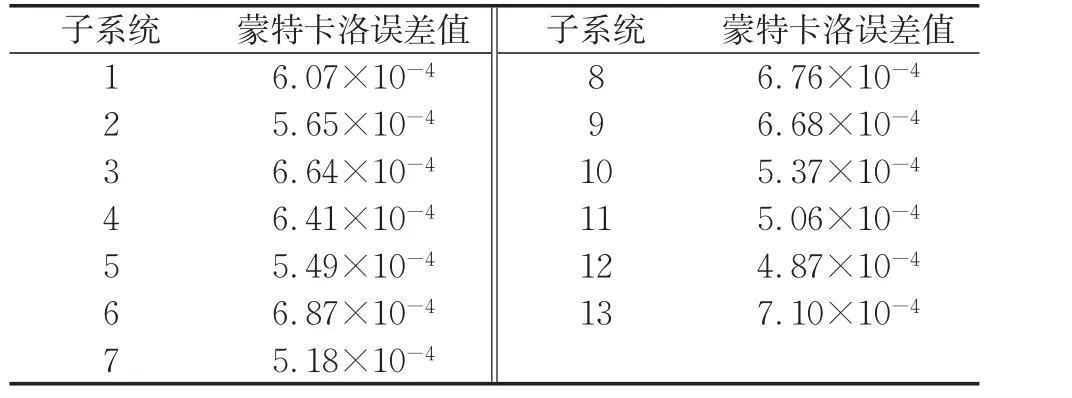
表5 各子系統泊松分布MCMC過程的MC error值Tab.5 MC errors for Poisson distribution for subsystems

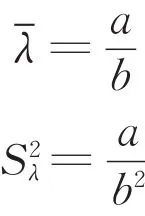
則其參數a，b可由下式給出：

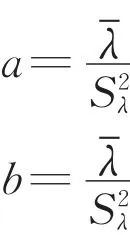
4.2.2 負二項分布假設

對于每一個子系統，假設其在25個月中，每個月發生的延期工作數量nt服從負二項分布，即

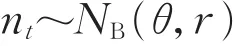
式中：t=1，2，…，25。

則似然函數形式為

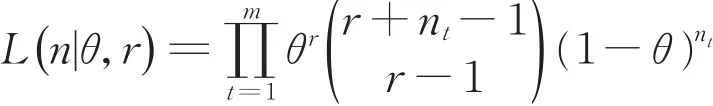
根據負二項分布的定義，參數θ為伯努利試驗“成功”的概率，而r則是表示在該負二項分布中“成功”的試驗數量；對于負二項分布參數θ，選取的共軛先驗分布為Beta分布β(a，b)。關于其超參數a，b的確定，亦采用以下兩種方式。

首先，使用類似于前述模糊先驗，即以往研究中多采用的先驗矩計算超參數a，b。具體來說，令Beta分布β(a，b)的均值和方差分別等于先驗均值和先驗方差，即

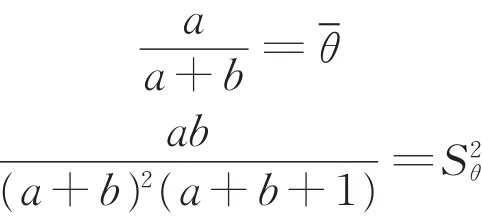
則可解得其超參數a，b的估計分別為

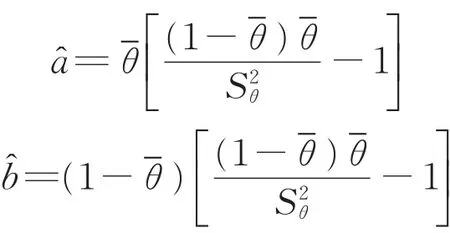
另外，還可采用無信息先驗分布確定超參數a，b。無信息先驗分布是指除了參數的取值范圍和參數在總體分布中的地位之外，再也不包含參數的任何信息的先驗分布。可以證明，Jefferys準則下，分布參數θ的無信息先驗分布為Beta分布β(0.5，0.5)；而Lindley準則下，參數θ的無信息先驗分布為Beta分布β(0，0)。事實上，從貝葉斯估計風險角度看，β(1，1)，β(0.5，0.5)及β(0，0)三種無信息先驗分布都具有較小估計風險［13］，都是合理可用的。目前無論是統計理論研究還是應用研究，無信息先驗分布的采用越來越多，被認為是“客觀”和可接受的，這也是貝葉斯統計學派近幾十年研究中最成功的部分之一［14］。在這里，由于Beta分布刻畫的是一個取值在（0，1）的參數，則其方差不宜過大，同時，固定超參數a，b的取值，構成U型Beta先驗分布，以此表示先驗信息的有限［12］，因此本文選用Beta(0.5，0.5)作為負二項分布參數θ的無信息先驗，即

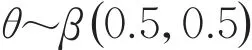
對于負二項分布的參數r，所選取的先驗分布為泊松分布，并且根據負二項分布定義，參數r應當為正整數，因此，可令

其中t(v)表示對于v取整。采用前述模糊先驗，本研究中利用案例數據的先驗矩計算超參數h。具體來說，令泊松分布P(h)的均值等于先驗均值-r，即可求得超參數h。最終確定的超參數h取值如表6所示。

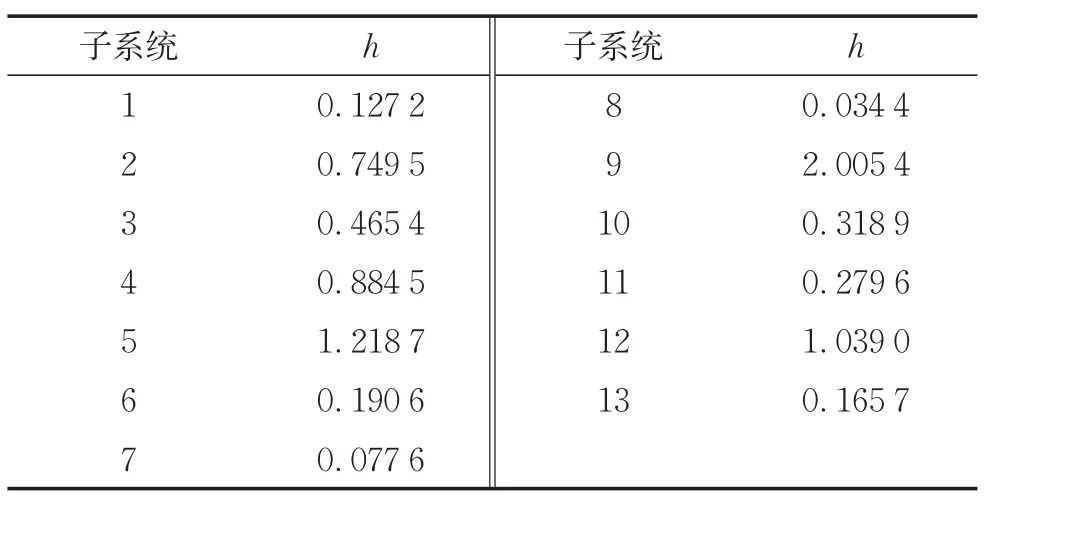
表6 各子系統負二項分布先驗下的超參數h取值Tab.6 Hyperparameterhfor negative binomial prior

以4號子系統“衛星廳港灣機坪飛行區工程”為例，經MCMC抽樣算法（具體為Metropolis Hastings算法）抽樣之后，參數θ與r樣本路徑如圖7所示。

參數θ與r的后驗抽樣樣本路徑較為特殊的原因在于，參數r必須取整數值，而在抽樣算法中參數θ與r是聯動變化，同時進行更新迭代的，因此其路徑形成如圖7所示形態。

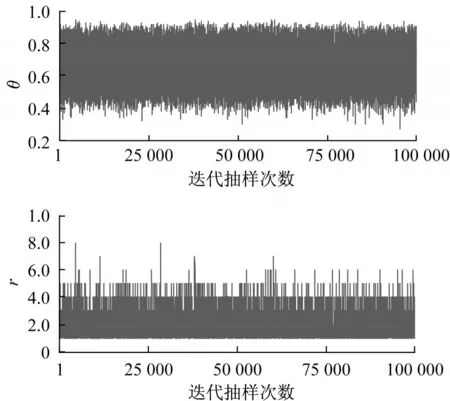
圖7 負二項分布參數的后驗抽樣樣本路徑（4號子系統）Fig.7 Parameter sample paths for negative binomial distribution(Subsystem 4)

圖8 和圖9分別為去掉前20 000個burn-in過程樣本后，參數θ的邊際后驗密度圖與參數r的邊際后驗直方圖。一般情況下，多峰的密度圖可能是由于馬爾科夫鏈未收斂，或者與數據相沖突的過強先驗假設所導致［11］，然而在本例中，多峰現象則是由于負二項分布參數θ與r的內在聯系，因此算法當中θ與r聯動構造，同時進行更新迭代。可以看到，參數θ的后驗密度圖的兩個波峰（modal value），分別與參數r的后驗頻率分布直方圖中頻率最高的兩個r值相對應。圖10為參數θ與r的自相關圖（ACF圖），兩者皆呈現出一個隨著Lag值增大，相對緩慢下降，最終趨近于0的過程。相似的下降過程也反映出Metropolis Hastings抽樣算法構造當中參數θ與r的關聯，趨近于0的自相關函數值是算法收斂的必要條件。

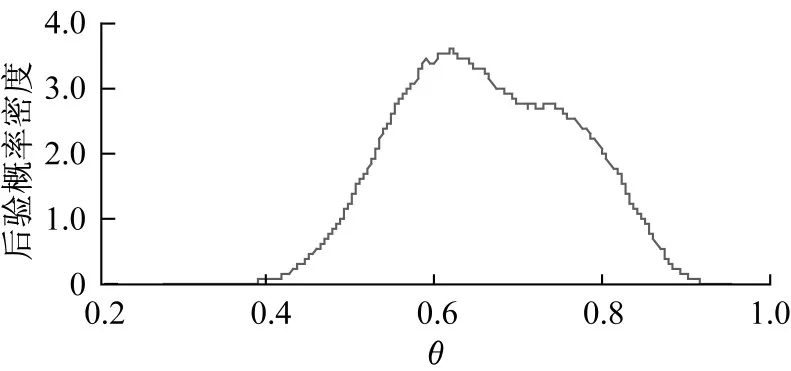
圖8 負二項分布參數θ的后驗密度估計圖（4號子系統）Fig.8Density plot for parameter θ (Subsystem 4)

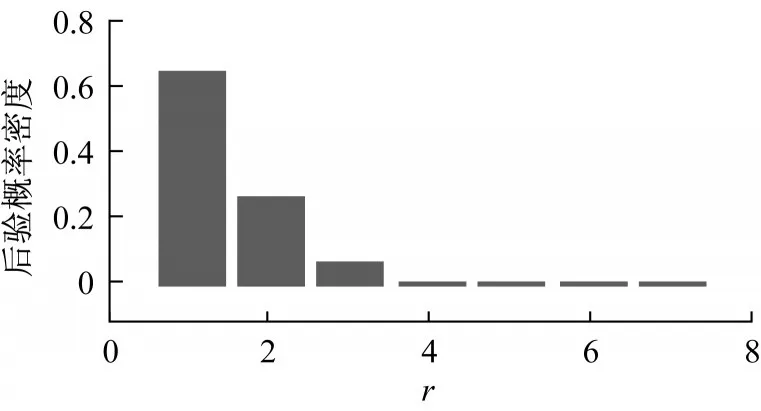
圖9 負二項分布參數r的后驗頻率分布直方圖（4號子系統）Fig.9 Frequency distribution histogram for parameter r(Subsystem 4)

基于本案例數據，對于各個子系統，參數θ與r后驗抽樣過程中計算得出的MC errors以及遍歷均值（ergodic mean）結果，能夠共同證明算法的收斂性，分析過程類似上文所述，這里不再展示。最終，去掉前20 000個burn-in過程樣本后，以80 000個模擬抽樣樣本計算，分別得到了在泊松分布假設與負二項分布假設之下，參數的貝葉斯后驗估計值（后驗均值）如表7所示。

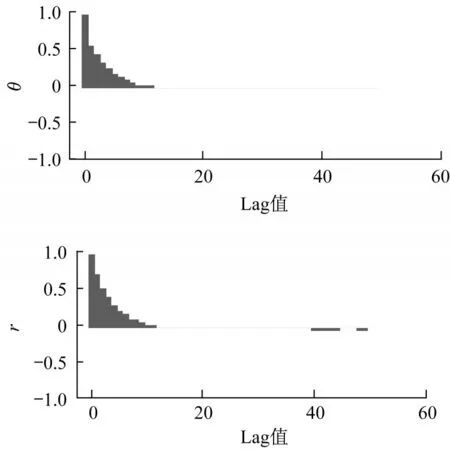
圖10 負二項分布MCMC過程自相關圖（4號子系統）Fig.10 Autocorrelation plot for negative binomial distribution(Subsystem 4)

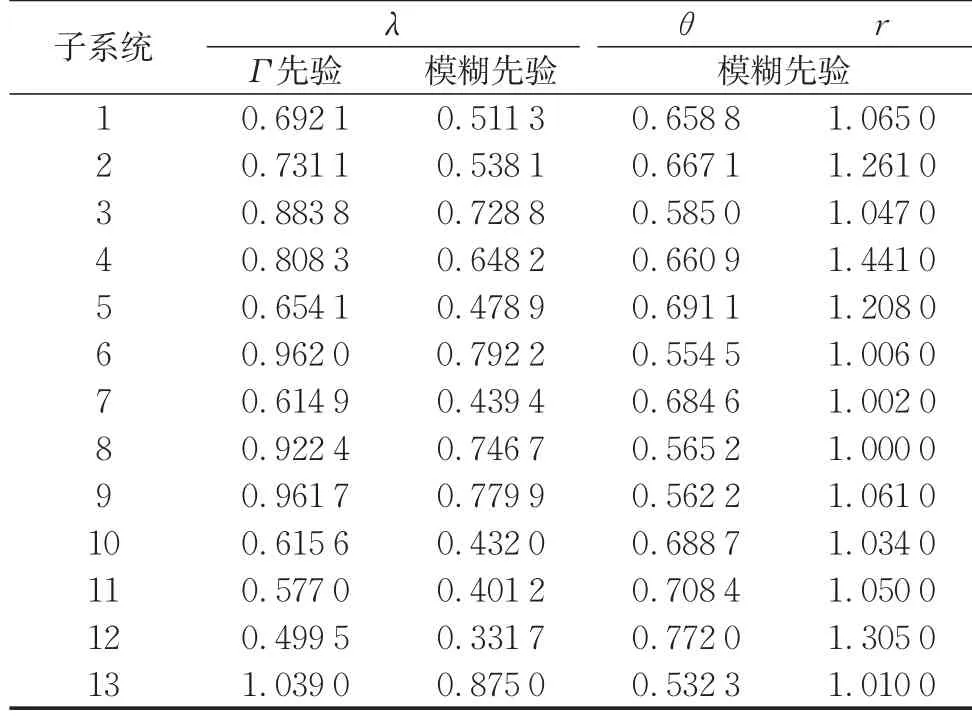
表7 各子系統延期頻數分布參數的貝葉斯估計值Tab.7 Parameters of frequency distributions estimated with Bayesian approach

5 結果分析

以上分布參數貝葉斯估計詳細過程，給出了先驗類型選擇、超參數設定、算法收斂判斷等貝葉斯估計步驟及結果，證明了其可行性。由圖11可知，從貝葉斯參數估計結果和極大似然（MLE）參數估計結果對比來看，在當前數據下，各子系統間的MLE估計結果差別較大，而貝葉斯方法減少了估計結果的波動性，這與金融領域類似應用研究［15］的結論相一致，即相對于極大似然估計，結合歷史數據和先驗信息的貝葉斯估計結果在低違約率事件違約頻數建模和預測方面具有穩健性優勢。機場建設工程總進度數據也具有獲取難度大，案例數量有限的特征，因此在使用離散分布刻畫進度違約可能時，分布參數的貝葉斯估計方法應當作為傳統估計方法的必要補充。這有助于管理者更好地理解機場建設總進度計劃進度違約發生規律。

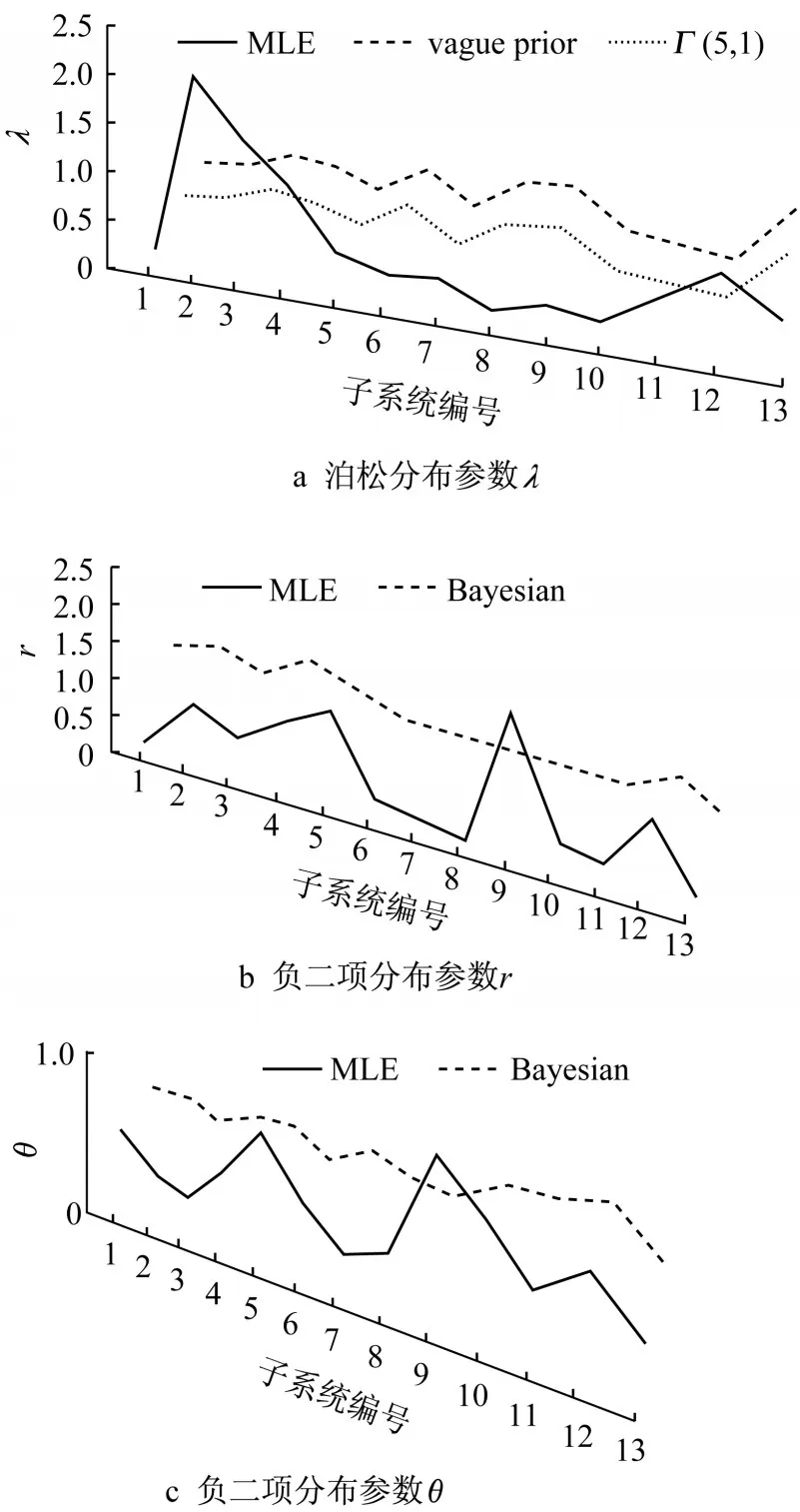
圖11 延期發生頻數分布參數MLE估計值與貝葉斯估計值Fig.11 MLE and MCMC estimates for frequency distributions

采用泊松分布假設估計分布參數時，貝葉斯估計過程采用了兩種先驗，得到的結果十分相似（圖11a），但是其后驗估計結果都與MLE結果不相類似。而相比之下，負二項分布參數的貝葉斯估計結果與MLE結果比較接近，這表現在各個子系統參數的絕對值和相對值上（圖11b、11c）。這說明在應用泊松分布假設時還需要更多準確先驗知識的使用，完善泊松分布形式、參數及其先驗的設定，例如采用其他形式的超先驗分布，或新加入超參數去納入更多的先驗信息［11］。相比較而言，利用負二項分布先驗，貝葉斯估計結果與MLE結果較為接近。若假設該工程樣本數據具有代表性，則說明負二項分布能夠較好地刻畫超期工作發生頻數，觀察進度違約月度數據，其方差相對均值較大，存在過離散（overdispersion）趨勢，這也是負二項分布能夠較好適用的原因之一［7，15］。另外，本案例中觀察到的樣本數據可能只部分地反應機場建設工程總進度計劃延期工作發生的客觀規律，那么需要更多后續案例的數據來進行建模和驗證（validation）［16］，而可更新性也正是貝葉斯模型的優勢之一。

6 結語

基于工程實踐提出一種刻畫機場建設工程總進度計劃延期發生風險的模型；并利用實踐歷史數據，通過MCMC方法的實施說明貝葉斯分布參數估計的可行性和操作過程，估計結果證明了貝葉斯方法的穩健性優勢和必要性。該分布模型可以幫助管理者理解在現有機場建設項目總進度計劃工作分解框架及工期目標之下，不同子系統中的工作活動發生延期的可能性，并可根據實際發生數據不斷更新模型。模型有助于管理者對按期完成難度較大的工作適度增加關注和投入，保證總進度計劃順利實施；在新制訂總進度計劃時，關于延期發生可能的信息也有助于給各子系統分配合理的工期。例如，在目標允許的情況下，給延期發生可能較高的子系統適當增加工期，提高計劃按時完成的概率，避免延期引起的超額投入和其他問題。需要指出的是，本研究所構建的基于風險隨機假設、根據工程實踐定量數據、宏觀刻畫進度風險可能性的概率模型，應當作為機場建設項目總進度計劃制訂、管理和風險預測的輔助手段。但與概率風險模型在其他任何行業的應用相同，其在機場建設項目中的應用也必須結合定性研究結論和其他手段，以保證有效性。例如進度違約的具體原因、子系統間的相互制約、延期工作的改進方向等微觀具體問題需要進一步案例研究和實踐總結來揭示。后續研究中，通過關于先驗知識獲取及先驗分布確定的進一步研究，可以將更多定性數據、專家知識引入模型［12］；通過建立泊松回歸、負二項回歸等回歸模型，可實現大型建設工程各總進度計劃超期風險影響因素的判別；另外，在掌握超期頻數的基礎上，結合超期所造成損失的嚴重程度，可以實現對進度風險更進一步的刻畫和分析［17-19］。