基于樣本依賴代價矩陣的小微企業信用評估方法

2020-02-12 11:02:54汪御寒張玥杰

同濟大學學報(自然科學版) 2020年1期

關鍵詞：模型

張濤，汪御寒，李凱，張玥杰

（1.上海財經大學信息管理與工程學院，上海200433；2.上海財經大學上海市金融信息技術研究重點實驗室，上海200433；3.復旦大學計算機科學技術學院，上海200433；4.復旦大學上海市智能信息處理重點實驗室，上海200433）

隨著金融業的發展，其服務范圍和方式日益豐富。聯合國于2005年提出普惠金融的概念，小微企業是普惠金融重點關注對象之一。我國近年來加大了對小微企業的扶持力度，鼓勵商業銀行對小微企業的借貸服務。小微企業本身暗含較高的風險，建立科學的信用評估系統對風險進行精準判別，對金融機構來說至關重要。一般金融機構對小微企業風控嚴苛，導致可用的違約客戶數據集規模較小，類別不平衡程度較高。基于這類信息不充分的數據集，構建泛化性能較好的模型具有較高的理論和應用價值，有助于金融機構識別劣質客戶，更好地服務優質客戶，從而促進市場經濟的發展。

國內外對于信用評估已有較豐富的研究，主要根據一些財務指標計算結合專家意見形成模型，而今，結合機器學習技術建模已成趨勢。West［1］建立了基于神經網絡的信用評估模型，指出多專家模型和徑向基函數神經網絡模型有更好的表現。肖文兵等［2］使用SVM（support vector machine）進行個人信用評估，取得了較高的分類準確率。Bhattacharyya等［3］使用SVM算法、隨機森林算法和邏輯回歸算法對信用卡欺詐數據分類預測。鄧超等［4］利用貝葉斯界定折疊法有效解決因樣本有偏引起的小企業信用評分模型分類能力喪失問題，增強了對樣本填補率和模型分類能力。Lessmann等［5］系統闡釋了信用評估領域的研究近況，指出異質集成學習的優越性。肖斌卿等［6］提出基于模糊神經網絡開展小微企業信用評級研究，以某農村商業銀行小微企業信貸微觀數據為樣本，實證驗證了模型在小微企業信用評級中可獲得更高的精度。為提高模型預測精度，在特征篩選方面，學者們做了不同方面的研究。熊志斌［7］提出在傳統 CFS（correlation-based feature selection）算法中引入Gebelein最大相關系數，結合支持向量機，構建了GCFS-SVM（Gebelein CFSSVM）模型，該模型可對非線性數據進行有效的特征提取，分類預測效果較好。Vlasselaer等［8］提出同時關注數據內在特征和交易關系網絡特征的特征提取方法，結合邏輯回歸、神經網絡和隨機森林建模，獲取了對異常交易較好的識別效果。Dahiya等［9］將特征選擇和混合Bagging（bootstrap aggregating）模型結合，使用卡方檢驗對非數值型數據進行特征篩選，而對于數值型數據，使用主成分分析。Chen等［10］分別將 LDA（latent dirichlet allocation）、決策樹、粗糙集以及F-score方法和SVM結合構建模型，提升了單個SVM模型的性能。特征篩選通常能在數據維數大、信息冗余的情況下提升模型性能，而建模面對的數據集信息有時是不完全的，Guo等［11］詳細介紹了信用風險模型中不完整信息和延遲過濾的概念。肖進等［12］根據信息完整度劃分訓練集，依據數據缺失程度確定特征的權重，根據權重對特征進行隨機選擇，充分利用了數據信息。關于算法的研究，國內外研究者們主要采用集成學習方法來提升模型性能。Kültür等［13］基于SVM、KStar、決策樹、隨機森林、樸素貝葉斯和貝葉斯網絡等傳統模型，分別使用樂觀的投票策略、悲觀的投票策略和權重投票策略進行集成學習，檢測信用卡欺詐。Xiao等［14］提出ECSC（ensemble classification approach based on supervised clustering）策略，先將數據集進行有監督聚類，在不同數據集上訓練模型，再分配權重構建集成學習模型。Ala′raj等［15］則在進行集成學習中考慮到基分類器之間的關系，相較于傳統集成策略，對錯誤預測有一定的修正效果。

對金融機構而言，一個有效的模型需要充分考慮利潤因素而不僅僅是分類準確率。Verbraken等［16］提出基于利潤的分類方法，以授信預期收益作為度量模型性能的一個因素。信用問題中對于違約客戶的誤判代價遠高于正常客戶的誤判代價，而通常情況下，違約客戶數目又遠少于正常客戶。因此，信用評估問題是代價敏感的，也是類別不平衡的。對于這類問題，可從數據角度采用重采樣技術改變樣本分布，使其趨于類別平衡，提高模型對正樣本的關注度。重采樣技術包括欠采樣和過采樣。欠采樣減少樣本集中負樣本的數量，而傳統基于隨機抽樣的欠采樣方式會丟失大量信息，Ng等［17］提出DSUS（diversified sensitivity undersampling）方法，使用該方法欠采樣可有效保留富含信息的樣本，有利于建模。將原始數據集分布的數據處理方法與集成學習結合往往可以獲取不錯的效果，鄒權等［18］將負樣本均勻分割，依次與正樣本合成訓練集，使用不同算法構建基分類器，最終用投票策略建立集成學習模型。與欠采樣方法相反，過采樣方法增加訓練集中正樣本的數量，其中，SMOTE（synthetic minority oversampling technique）算法被廣泛應用［19］。林舒楊等［20］對負樣本進行K均值聚類，提取與正樣本數目相當的聚類中心，結合SMOTE算法對樣本進行適度過采樣，有效避免樣本過度稀疏。Sun等［21］提出 DTE-SBD（decision tree ensemble based on SMOTE，bagging and differentiated sampling rates）模型，利用SMOTE算法按照不同比例對數據集進行過采樣，提高了集成學習基礎分類器之間的多樣性。另外，不少學者直接在算法層面改進傳統機器學習方法，使其可有效應對代價敏感問題。Chung等［22］結合貝葉斯決策理論，修改SVM函數方程，使其獲取的決策超平面與樣本分布有關，通過超平面的偏移可使模型更多地識別正類樣本。Bahnsen等［23-24］提出基于最小風險貝葉斯概率計算準則的分類器，可有效降低模型誤分類帶來的代價。閆明松等［25］以C4.5決策樹為基算法，對代價敏感決策樹和多個代價敏感Boosting算法進行了系統的對比。Hulse等［26］基于Adaboost算法，提出AsymBoost算法。關于代價敏感學習中的代價，之前的研究往往單純定義兩類樣本的誤分代價，近些年，學者們開始關注到具體針對個體的誤分代價。Bahnsen等［27］在信用評估領域提出計算與特征有關的樣本依賴的代價矩陣，使用該方法可更科學地表征代價，改善代價敏感模型性能。除了誤分類帶來的經濟意義上的代價，一些學者還考慮到模型訓練的代價，在大規模數據集建模時，權衡學習時間代價、模型維護代價和誤分類代價有重要意義［28］。Yang等［29］對于具有缺失值的屬性，考量獲取該缺失值對于整體精度的提升度和耗費代價的關系，以建立整體代價最小的模型。

當信用數據規模較小時，對于類別不平衡問題，采用欠采樣會導致模型訓練所用信息不足，而僅對正樣本的過采樣易導致過擬合。本文在之前學者研究的基礎上，提出樣本依賴的SXG-BMR模型，同時對正負樣本進行低倍率過采樣，使樣本分布明晰的同時有效避免了過擬合，以集成學習為基本模型，基于樣本依賴代價矩陣，利用最小貝葉斯風險決策框架在模型中引入更符合實際的代價，大大提高了模型對于正樣本的識別能力，可有效提高信用評估模型的性能。

1 樣本依賴代價敏感模型的數據策略

類別不平衡問題是信用評估領域普遍需要面對的問題，而由于小微企業自身的特殊性，其信用評估過程中該問題更為突出。銀行往往會主觀上拒絕對小微企業的信貸以防控風險，導致歷史數據集的整體數據量較少；同時，銀行對小微企業的借貸要求往往更為嚴格，導致歷史數據集中的正樣本數目極少，類別不平衡的程度較高。為了應對這一問題，本文采用樣本依賴的代價敏感模型框架。在數據層面上，代價敏感模型訓練的輸入包括數據集和代價敏感矩陣集。本文對整體樣本進行過采樣以明晰樣本分布，并依據數據特征，針對每一個樣本計算其代價矩陣，以更為精確地衡量代價。

1.1 整體樣本過采樣

SMOTE算法是過采樣方法中的經典算法，其基本思想是在樣本和其鄰近同類樣本連線上隨機插入新的同類樣本［19］。在應對類別不平衡問題上，SMOTE方法多被用于生成少數類樣本，以平衡數據集。但在樣本集規模較小的情況下，缺少的不只是正樣本的信息，負樣本的分布也很難由少數數據反映，正負樣本分界超平面較為模糊。若采用SMOTE算法僅僅對每個小類樣本進行過采樣，將會產生一定的盲目性現象，導致有些人工合成的小類樣本對大類樣本的泛化空間產生影響，降低分類效果［30］。另外，SMOTE方法僅對所有少數類樣本進行過采樣處理，未充分考慮不同樣本對分類平面的重要度的差異，易導致模型對正樣本的過適應，將可能使分類器出現過擬合現象［31-32］。

為此，本文提出基于SMOTE算法對整體樣本進行過采樣的方法，平衡了過采樣引入噪聲以及降采樣丟失樣本的矛盾。其基本思路如下：采用SMOTE算法對整個樣本集進行處理，同時生成正、負樣本，樣本生成比例可視實際問題數據規模而定。該方法可有效應對數據集過小或數據缺失的情況，使正負樣本分界面更為明顯，降低模型分類的難度，避免過擬合，提高模型的準確性。對于樣本集中每一個樣本，以樣本xi為例，找到其K個同類近鄰樣本zi1，zi2，…，ziK，按公式（1）隨機生成新的樣本：

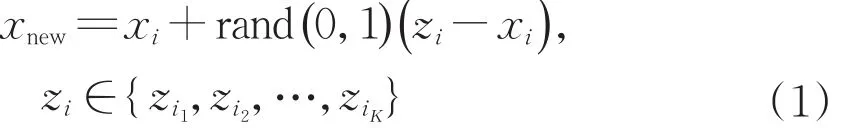
同時，根據UCI（University of California Irvine）信用數據集和上海市小微企業信用數據集的實驗結果，可以發現，通過利用SMOTE算法對樣本整體過采樣處理得到的結果優于僅僅利用SMOTE算法對正樣本進行過采樣的結果，并且能夠很好地實現精確率（Precision）和召回率（Recall）的平衡。

1.2 樣本依賴代價矩陣

代價矩陣是標識將樣本劃分為不同類別所導致代價的矩陣，諸如信用評估這類二分類問題，樣本xi的代價矩陣如表1所示。

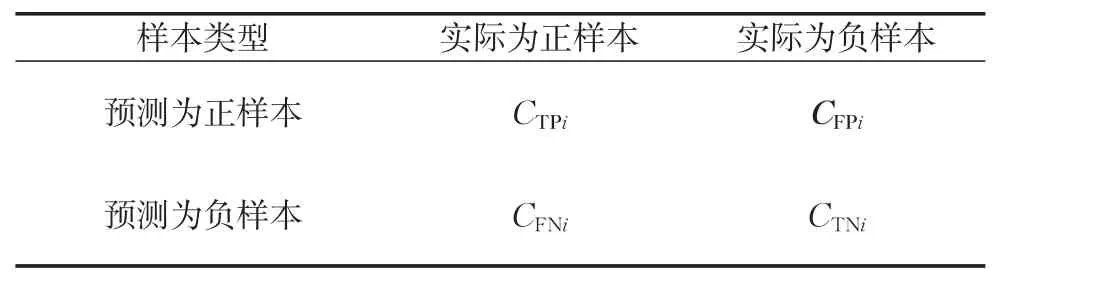
表1 樣本xi的代價矩陣Tab.1 Cost matrix of sample xi

表1中，CTPi、CFPi、CFPi、CFPi分別表示樣本xi不同預測結果導致的成本（代價）。關于代價敏感學習，在一些問題中，誤分的代價與樣本自身屬性有關，而不僅僅與類別有關，比如不同貸款額度會帶來不同的誤分代價。Bahnsen等［27］將正確分類的代價定為0，對錯誤分類的代價進行計算，提出了信用評估中的樣本依賴代價矩陣，如表2所示。其中，對于樣本xi，Ri表示損失優質客戶帶來的損失，可根據借款利率和客戶信用額度計算而得；CFPα基于資金不會閑置的假設，表示拒絕好的客戶選擇其他客戶可能帶來的潛在損失，可根據市場上的平均信用額度和平均利潤率計算；cli表示其信用額度，可根據客戶償債能力的指標計算得到；Lgd表示壞賬帶來的損失占信用額度的比率，Bahnsen等在研究中擬定了Lgd為75%。通過這種規則可得出所有樣本的代價矩陣，每個矩陣都是根據個體的情況計算，更精確地描述了誤分類帶來的代價。

表2 樣本xi的樣本依賴代價矩陣Tab.2 Sample-dependent cost matrix of sample xi

為了更貼近實際代價，本文根據所研究數據集所包含的特征以及市場情況，提出了相應的代價矩陣計算方法，該方法與貸款額度和樣本類別比例有關，這樣可以跟隨樣本集中兩類樣本的比例，調整模型對正樣本的關注度，有利于提升模型的性能。對于樣本xi代價矩陣中的CFPi的計算，基于資金不會閑置的假設，拒絕該客戶后，將會貸給其他客戶，以樣本集的平均貸款額度表示將該資金貸給其他客戶的額度，以樣本集的平均貸款時間作為貸給其他客戶的時間，以樣本集的平均貸款利率作為貸給其他客戶的利率，以樣本中正負樣本的頻率分別作為貸給劣質客戶和優質客戶的概率。因此，本文設計樣本依賴代價如下：

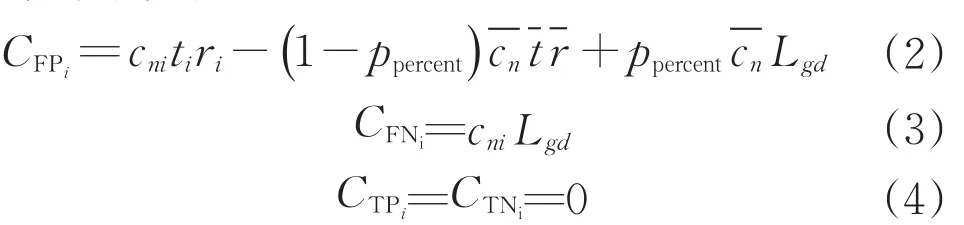
式中：cni為樣本xi的貸款額度；ti為樣本xi的貸款時間；ri為其貸款利率為樣本集平均貸款額度為平均貸款時間為平均貸款利率；ppercent為樣本集中的正樣本所占比例。

2 基于樣本依賴的SXG-BMR模型

鑒于 XGBoost（Extreme Gradient Boosting）算法可充分利用信息又能防止過擬合，本文構造基于最小風險貝葉斯決策的代價敏感學習框架，采用XGBoost算法，并結合前文的數據策略，提出樣本依賴的SXG-BMR模型。

2.1 最小風險貝葉斯決策

進一步，引入風險代價因素，以整體風險最小化為目的優化模型，即為最小風險貝葉斯決策，應用于代價敏感學習問題，可提升模型決策性能［23］。記將屬于ωj類的樣本歸于ωk類帶來的風險為λkj。對于某個樣本xi，求解式（6）得到λk*，進而得到相對應的k*，而相應的類ωk*即為樣本xi的最終類別。

式中：p(ω)=(p(ω1|xi)，p(ω2|xi)，…，p(ωu|xi))；λk=(λk1，λk2，…，λku)。

2.2 XGBoost算法

XGBoost算法是梯度提升算法的一種優化實現形式，由Chen等提出并實現［33］。其目標函數包括損失函數和正則項，在進行學習迭代更新時考慮二階導數信息，可更快地優化目標函數。同時，在目標函數中加入正則項，可控制模型復雜度，有效防止過擬合。本文應對的數據集，一方面數據規模較小，需要被充分地學習；另一方面，為提升模型對樣本的識別能力，對數據集進行了一定程度的過采樣，建模有過擬合的風險。在這種情況下，XGBoost是一種較為理想的算法。對XGBoost的設計如下：

對于數據集{(x1，y1)，(x2，y2)，…，(xn，yn)}，xi為樣本，yi為樣本xi的真實值，y^i為樣本xi的預測結果，i∈{1，2，…，n}。設初始狀態設為，則

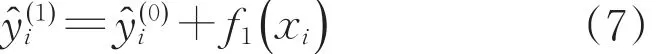
第m次迭代后，

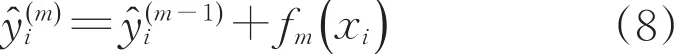
式中：y^(m)i為第m輪后對樣本xi的預測結果；fm為第m輪迭代的分類器，fm∈F，F為分類器集合。

第m次迭代，XGBoost的目標函數如式（9）所示。

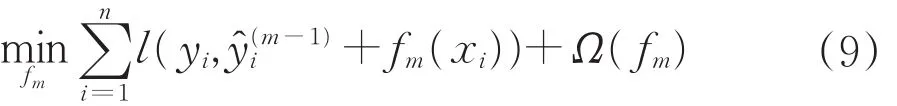
式中：l為損失函數，Ω為正則項。考慮二階信息，對目標函數進行泰勒展開，舍去常數項，得到新的目標函數，如公式（10）所示。

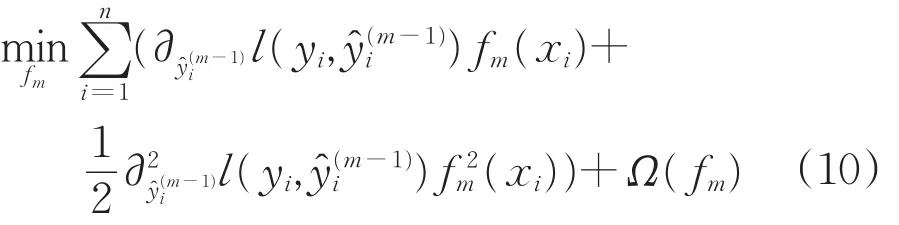
每次迭代求解得到fm，迭代M次之后，獲取最終分類器y^(M)，如公式（11）所示。

2.3 樣本依賴的SXG-BMR算法流程

本文基于XGBoost算法，結合數據過采樣的預處理方式，利用樣本依賴代價矩陣和最小風險貝葉斯決策，將代價敏感元素引入模型，從而構建了樣本依賴的SXG-BMR模型。以0表征負樣本（正常客戶）類別，1表示正樣本（違約客戶）類別，具體決策流程如下：

（1）利用SMOTE算法對訓練集進行整體過采樣，得到新的樣本集合，過采樣比例根據樣本規模而定。

（2）對于樣本集合中每一個樣本xi，計算其樣本依賴代價矩陣(CFPi，CFNi，0，0)。

（3）利用XGBoost算法訓練模型，得出將樣本xi的預測為負類的概率

（4）獲取樣本xi的樣本依賴代價矩陣(CFPi，CFNi，0，0)。

（5）計算對樣本xi的分類預測平均代價：

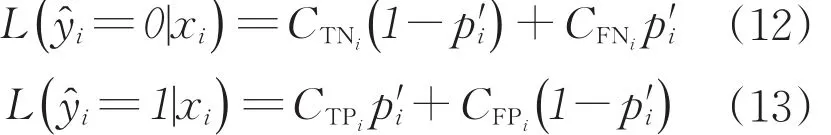
依據最小風險貝葉斯準則進行決策，將樣本xi判定為預測代價小的類別。

值得說明的是，本文較為簡單直接地根據客戶信用額度、借貸時間兩個屬性進行樣本依賴代價矩陣的計算，該方法具有較好的普適性。當然，代價矩陣也可由數據集給出，也可根據樣本比例自行定義，兩類樣本比例差別越大，對正樣本賦予的關注度越高，代價矩陣中CFN的值應越大。在實際操作中，如果無法獲取代價矩陣，可通過不斷調整參數，選出在數據集上表現最好的代價矩陣建立模型。如果不考慮代價矩陣，則模型相當于加入了SMOTE對整個樣本處理的貝葉斯最小錯誤率決策，對于增強小樣本集的模型分類性能也有一定的參考價值。

3 實驗分析

本文使用了兩個數據集對提出的算法框架進行驗證。首先在UCI標準數據集上進行縱向、橫向對比，以驗證樣本依賴的SXG-BMR模型的性能。在對分類算法進行對比分析時，本文選用了較為經典的Adaboost、Gradient Boosting、神經網絡、決策樹、隨機森林、邏輯回歸方法，再分別對其進行最小風險貝葉斯決策的改進，以引入代價敏感學習算法，另外還選用了代價敏感決策樹和代價敏感隨機森林算法作為對比對象。數據處理層面，本文進行了僅用SMOTE算法對正樣本進行過采樣平衡數據和對整體數據進行過采樣的對比。對整體樣本的過采樣，不改變原始正負樣本比例，為防止過擬合，對整體樣本采用了較低的過采樣倍數。代價矩陣層面，進行了類別依賴矩陣和樣本依賴代價矩陣的對比。之后，本文將基于樣本依賴的SXG-BMR模型應用于上海市小微企業信用數據集中，通過對比實驗，進一步驗證了該模型的有效性。本文模型性能皆使用五折交叉驗證結果度量。

3.1 數據集

UCI信用數據集由Hofmann教授提供，共包含1 000個樣本，有20個屬性，樣本分布比例如表3所示。數據集描述了客戶的信用額度、貸款期限、借貸歷史、借款目的、年齡、房產、工作、婚姻狀況、國籍等信息，并提供了類別依賴的代價矩陣，如表4所示。

表3 UCI信用數據樣本分布情況Tab.3 Sample distribution of UCI credit data

表4 信用數據代價矩陣Tab.4 Cost matrix of credit data

上海市小微企業信用數據記錄了上海地區部分小微企業的歷史借款違約情況，原始數據有財務型屬性也有非財務型屬性，考慮到小微企業財務數據的真實性問題，數據中更側重于非財務型屬性，從企業的員工情況、組成結構、歷史行為等方面描述企業特征。屬性主要包括企業借貸金額、企業固定資產、大股東學歷、房產、車產、婚姻情況、高管學歷以及信用逾期情況、法人代表學歷信用逾期情況、員工學歷分布、企業繳納社保情況。共4 193條樣本，樣本分布情況如表5所示，樣本類別不平衡程度較嚴重。

表5 上海市小微企業信用數據樣本分布情況Tab.5 Sample distribution of credit data of smalland micro enterprises in Shanghai

3.2 模型性能度量指標

在信用評估領域，一個優質的模型應在盡可能識別有風險客戶的同時避免流失優質客戶，提高整體節約的代價。本文采用召回率（Recall）、精確率（Precision）、AUC（Area Under Curve，ROC曲線下的面積）和代價節省率Saving rate來度量模型性能。Recall和Precision定義如下：

式中：TP為實際正類，預測正類；FN為實際負類，預測正類。

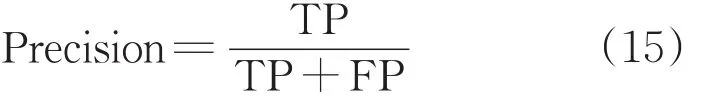
式中：FP為實際負類，預測正類。

代價節省率標識模型可度量節約代價的程度，本文將模型預測所產生的代價與將全部樣本預測為正或者負產生代價中較小值相比，來表征代價節省率。對于樣本集yi∈ {0，1}，i∈ {0，1，…，n}，使用分類器f(x)對T中樣本進行預測，得到預測類別集合{y^1，y^2，…，y^n}，其代價節省率計算如式（16）所示。

式中：Cost(f(T))表示按照分類器的預測結果所產生的代價。

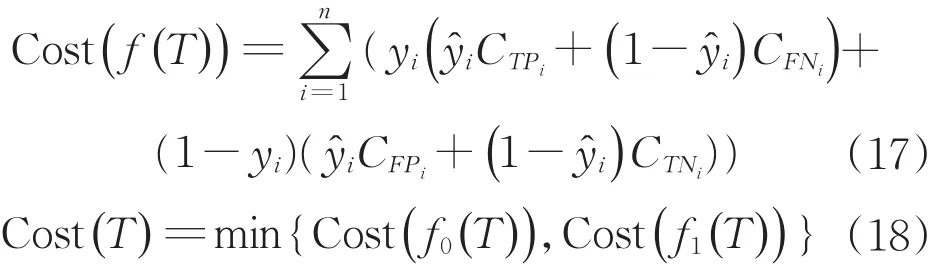
這里，Cost(f0(T))表示將所有樣本全部判定為負類所帶來的代價，Cost(f1(T))表示將所有樣本全部判定為正類所帶來的代價。

3.3 整體性能評估與比較

3.3.1 UCI信用數據集的實驗結果

本文進行了不對數據集采樣處理、對正樣本進行過采樣和對整個樣本集進行不同倍率過采樣的對比，以驗證用SMOTE算法對樣本整體過采樣的有效性。所使用訓練集的分布如表6所示。

表6 實驗所用訓練集分布情況（UCI）Tab.6 Distribution of training sets used in experiments（UCI）

根據原始數據集中提供的代價矩陣，各分類器對于初始數據集的分類結果如表7所示。選用算法包括：AB（adaboost）、GB（gradient boosting）、XG（XGBoost）、LR（logistic regression）、NN（neural network），RF（random forest）、DT（decision tree）、BMR（對模型引入Bayes minimum risk）、CS-DT（cost sensitive decision tree）和CS-RF（cost sensitive random forest）。

由表7可以看出，在未引入代價敏感元素的分類器中，各分類器效果表現均不佳，且代價節省率多為負值。在引入最小風險貝葉斯決策之后，各分類器的代價節省率有所提升，但其整體表現依然并不夠理想，其Saving rate值均小于0.2。雖然各分類器的Recall值明顯增大，均接近1，但是，引入最小風險貝葉斯決策之后的各分類器的Precision值比未引入代價敏感元素均偏小。這是因為該數據集的正負誤分類代價比統一為1：5，而總體樣本數目較少，模型無法準確得到正負樣本的分布規律，導致各模型對負樣本過于敏感。所以，在引入最小風險貝葉斯決策之后，各分類器的Recall值明顯增大，但Precision值顯著減小，AUC值也有所下降。

本文以市場一年期貸款利率為4.75%，默認壞賬損失金額率為75%，計算樣本依賴代價矩陣。引入樣本依賴代價矩陣后，各代價敏感模型性能如表8所示，結果顯示其性能優于未引入代價敏感元素的原始模型，也優于基于類別依賴矩陣的代價敏感模型，取得了Precision和Recall的平衡，提升了AUC以及代價節省率。其中XG-BMR模型表現相對較好，各性能度量指標數值較為均衡，且都優于其他模型，代價節省率高達0.434。

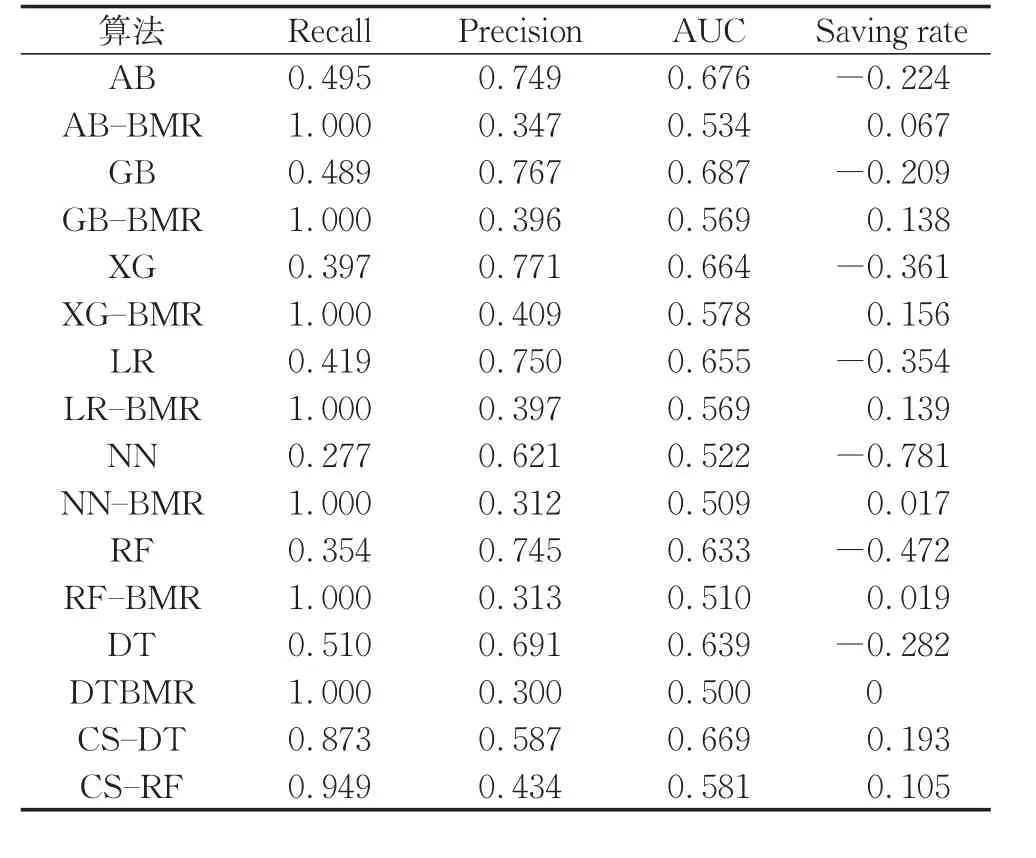
表7 原始數據集上各模型性能表現（UCI）Tab.7 Performance of models on original data sets（UCI）

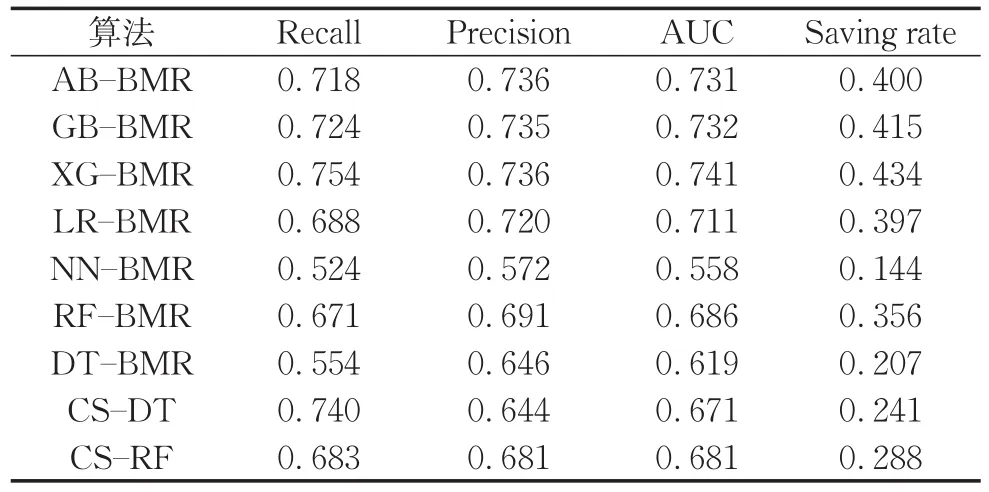
表8 樣本依賴的代價敏感模型性能表現（UCI）Tab.8 Performance of sample-dependent cost sensitive models（UCI）

選取性能表現相對較好的模型AB-BMR、GBBMR、XG-BMR、LR-BMR、RF-BMR、CS-DT和CS-RF，采用本文SMOTE方法處理數據集后，各模型在各數據集上的性能表現如表9所示。

從表9可以看出，利用SMOTE算法對樣本整體過采樣得到的結果優于利用SMOTE算法僅僅對正樣本進行過采樣得到的結果，使用SMOTE對整體數據集進行處理可以使各模型分類性能得到顯著提升。對整體數據集僅擴充一倍時，使用XG-BMR模型的 Recall達到 0.771，Precision為 0.751，AUC為0.757，優于傳統平衡數據集上訓練模型的效果，由于樣本個體代價差異，代價節省率稍弱于僅對正樣本過采樣的結果，但也已十分接近，這表明了對整體數據集過采樣的有效性。不過，高倍過采樣比例對模型性能代價提升效果有限，并未呈現明顯與過采樣比例正相關的關系，為了避免過擬合，對整體樣本過采樣程度以不超過4倍為宜。在這種情況下，基于三種Boosting算法的模型性能表現相對穩健，很好實現了Precision和Recall的平衡。其中，ABBMR模型在對整體樣本過采樣至四倍的數據集中獲得較優效果，GB-BMR對整體過采樣至三倍的數據集中獲得較優效果，而XG-BMR在對整體過采樣至兩倍的數據集中即獲取優于其余模型的表現。

因此，本實驗驗證了本文所提出的SXG-BMR模型的有效性，以及樣本依賴代價敏感數據策略對模型性能的提升作用。

3.3.2 上海市小微企業信用數據集的實驗結果

對于上海市小微企業數據集（SH），本部分實驗所用的數據集分別為原始數據集、使用SMOTE平衡數據集以及對整體數據樣本過采樣2～4倍的數據集，具體訓練集分布如表10所示。

代入市場貸款利率，計算出樣本依賴代價矩陣。對于缺失借貸時間的樣本，均默認為1年。各樣本依賴代價敏感模型在原始數據集中的結果如表11所示。

由表11可以發現，各模型沒有達到Recall和Precision很好的平衡。其中，AB-BMR、GB-BMR、XG-BMR和LR-BMR取得了較高的Recall，但Precision皆較低。而CS-RF取得了很高的Precision，為0.883，Recall卻僅有0.486。

選取在原始數據集中表現相對較好的ABBMR、GB-BMR、XG-BMR、LR-BMR、RF-BMR，采用SMOTE方法處理數據集后，各模型在各數據集上的性能表現如表12所示。

由表12可知，使用SMOTE方法僅對正樣本過采樣平衡數據集后，模型獲得了很高的Precision，但并沒有很好地識別正樣本，Recall相較于原始數據集大幅降低，有過擬合的傾向。而對整體樣本低倍率過采樣取得了較為均衡的效果，當數據集擴充至4倍時，XG-BMR模型Recall達0.937，Precision達0.713，AUC高達0.820，代價節省率為0.704，效果優于其他模型。同UCI信用數據集的實驗結果類似，利用SMOTE算法對樣本整體過采樣得到的結果優于利用SMOTE算法僅僅對正樣本進行過采樣得到的結果，并且能夠很好地實現各模型Precision和Recall的平衡。

本實驗進一步驗證了樣本依賴SXG-BMR模型可有效應對類別不平衡的信用數據，高效而精確地識別違約客戶，具有較好的實際應用價值。為防止過擬合，實驗中對整體數據集過采樣倍數控制在4倍以內，在實際應用中，也可根據實際情況適度調整過采樣倍數，以獲取更優的效果。

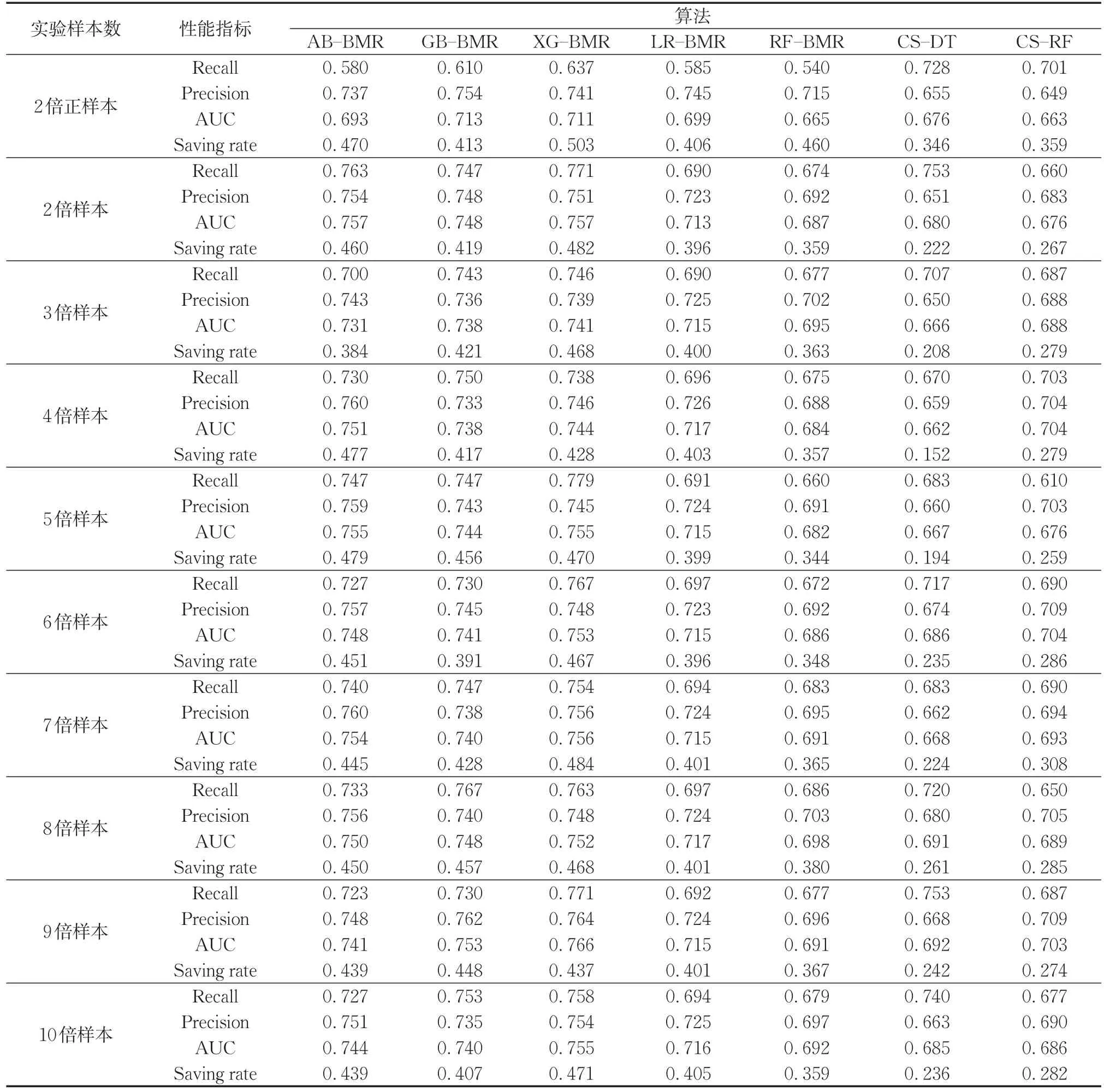
表9 樣本依賴的代價敏感模型在過采樣數據集的性能表現（UCI）Tab.9 Performance of sample-dependent cost sensitive model on oversampled data sets（UCI）

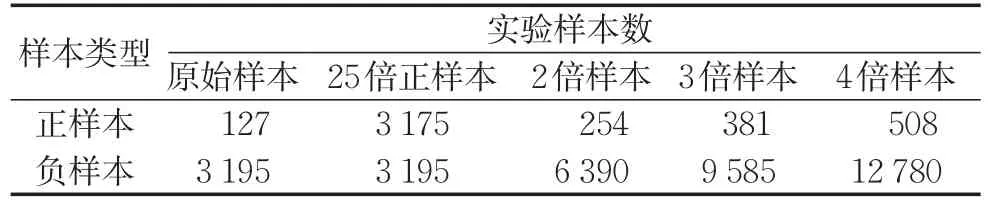
表10 實驗所用訓練集分布情況（SH）Tab.10 Distribution of training sets used in experiments（SH）

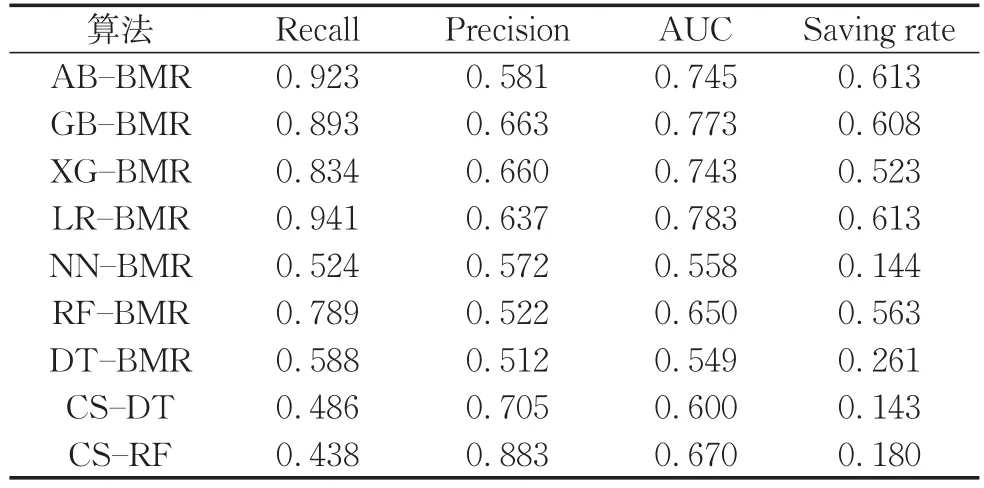
表11 樣本依賴的代價敏感模型性能表現（SH）Tab.11 Performance of sample-dependent cost sensitive models（SH）

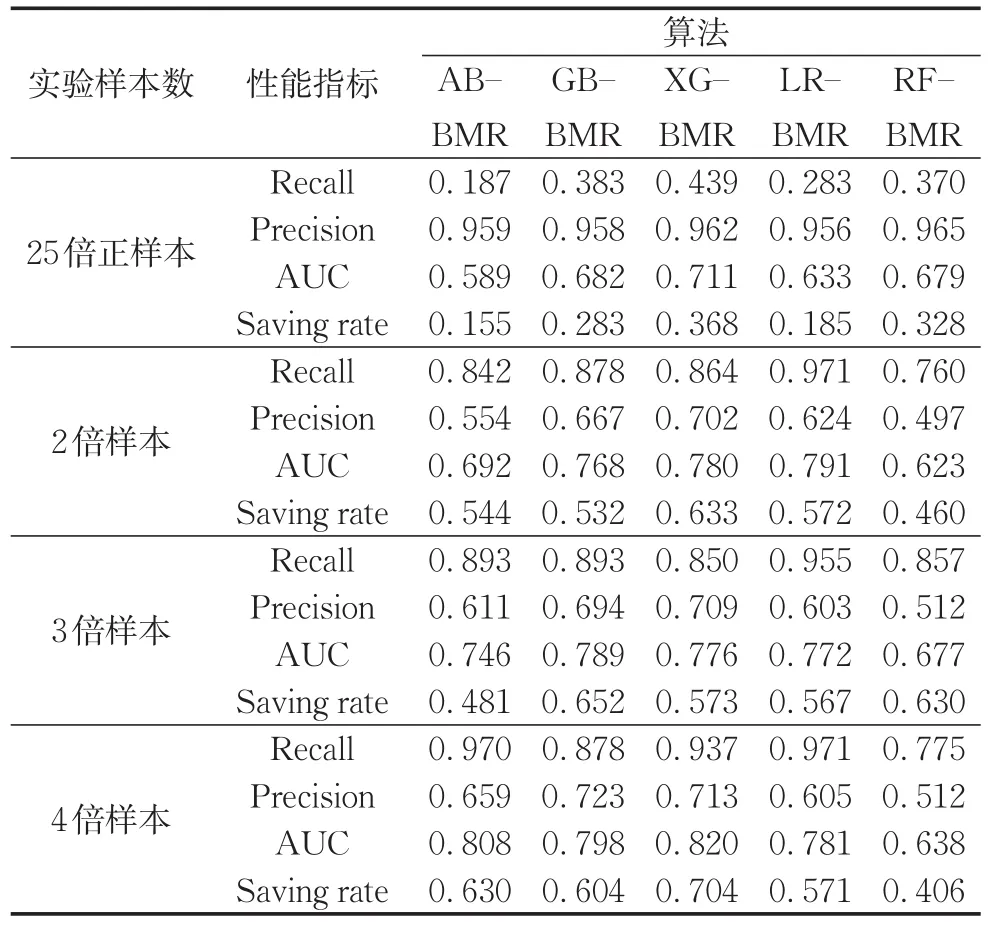
表12 樣本依賴的代價敏感模型在過采樣數據集的性能表現（SH）Tab.12 Performance of sample-dependent cost sensitive model on the oversampled data sets（SH）

4 結語

本文著眼于諸如小微企業這類數據集規模較小且類別不平衡的信用評估問題，改進傳統的機器學習算法框架進行代價敏感學習。數據處理上，為了緩解樣本中的噪聲信息以及過擬合問題，本文應用SMOTE算法對整體數據集進行適度過采樣，可在不產生過擬合的前提下令數據集的分布更明顯。為了使模型對代價敏感，本文使用了最小風險貝葉斯決策與基本分類器結合的框架，該框架下的模型訓練高效且性能較為穩健。在算法層面，構建了以集成學習算法為基礎的模型，采用XGBoost集成學習算法，通過實驗對比驗證了其優越性。另外，本文提出了一種適用小微企業的樣本依賴代價矩陣的構建方法，可應用于記錄了借貸額度屬性的信用數據集中。在實驗中對比了類別依賴代價矩陣和樣本依賴代價矩陣，驗證了后者對代價敏感學習模型的性能具有顯著提升作用。最后，本文提出樣本依賴的SXG-BMR模型，可為金融機構針對小微企業的信用評估提供參考。

未來研究可考慮結合特征篩選，使用相較于SMOTE算法更先進的算法合成數據。另外，可引入諸如收入、資產、關系網、借貸用途等更多特征，研究更為精準科學的信用評估領域的樣本依賴代價矩陣計算方法。總之，在互聯網技術飛速發展的今天，金融機構的風險防控、業務經營決策將越來越依賴于大數據和人工智能，科學的信用評估體系可以幫助金融機構高效準確地識別客戶類別，從而使優質企業獲取資金支持，促進經濟的良性發展。