立體幾何中動(dòng)態(tài)問(wèn)題的解題策略

>>>楊春輝

近幾年的高考試題中，立體幾何中的動(dòng)態(tài)問(wèn)題多次作為壓軸的客觀題出現(xiàn)。動(dòng)態(tài)問(wèn)題的起因大致分為兩類：平移與旋轉(zhuǎn)；而要解決的問(wèn)題主要有三類：一是面積、體積問(wèn)題，二是角度問(wèn)題，三是距離問(wèn)題。解決這類問(wèn)題需要非常強(qiáng)的空間想象能力和轉(zhuǎn)化能力，解題要在動(dòng)態(tài)中找到“靜”的一面，在變中找到“定”的一面，動(dòng)中求“靜”，變中求“定”。

一、幾何體表面上的動(dòng)點(diǎn)間的最短距離問(wèn)題

例1.已知各棱長(zhǎng)均為1的四面體ABCD中，E是AD的中點(diǎn)，P∈CE，則BP+DP的最小值為

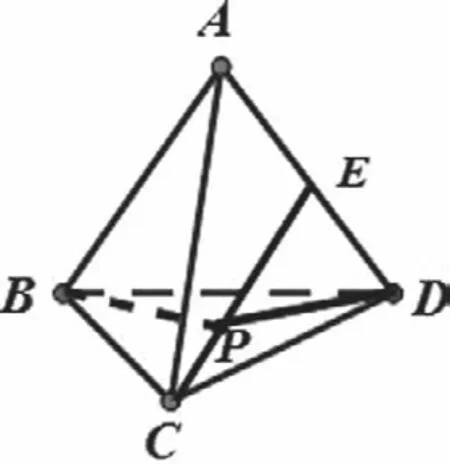
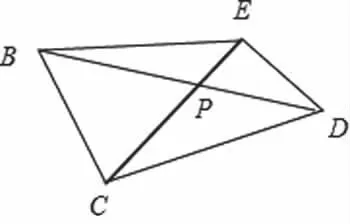
解析：把平面BEC及平面CED以CE為折線展平，三角形CED是正三角形的一半，故在平面DEBC中，連接BD，與EC相交于點(diǎn)P，則DP+BP為最短距離，再利用余弦定理即可得出.

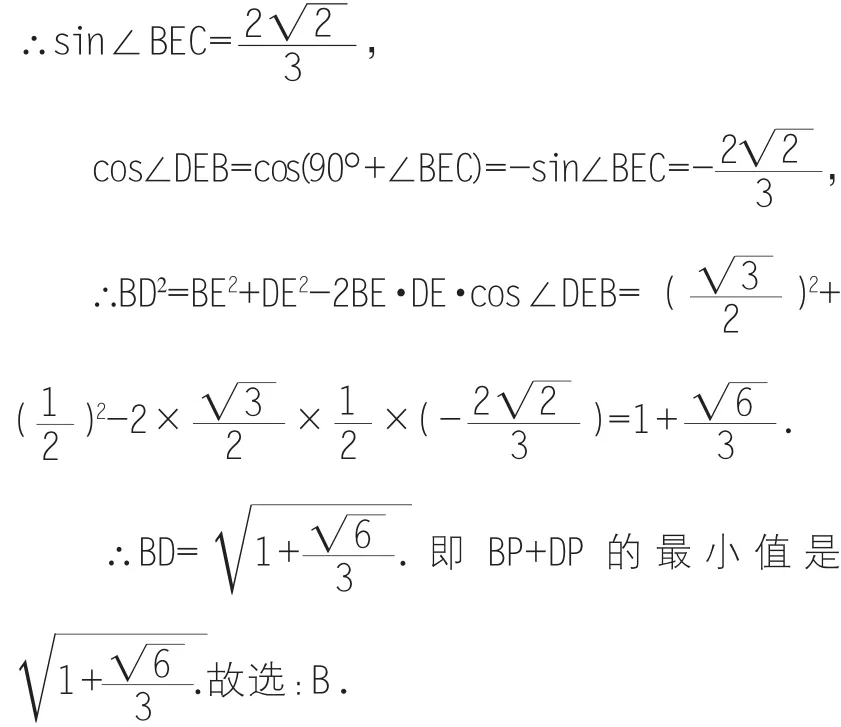
二、動(dòng)態(tài)中與形成的截面的面積有關(guān)的問(wèn)題

例2.長(zhǎng)方體 ABCD-A1B1C1D1中，已知 AA1=3，AB=AD=2，棱AD在平面α內(nèi)，則長(zhǎng)方體在平面α內(nèi)的射影所構(gòu)成的圖形面積的取值范圍是_______.

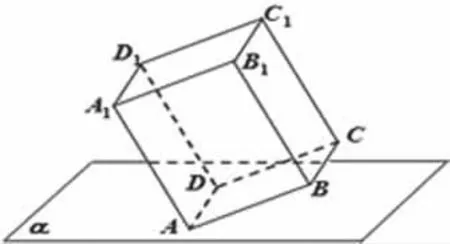
解析：由題意，四邊形ABCD和ADD1A1的面積分別為4和6.

若記平面ABCD與α平面所成角為θ，則平面ADD1A1與平面α所成角為-θ.它們?cè)谄矫姒羶?nèi)的射影的面積分別為 4cosθ 和 6cos（-θ）=6sinθ，所以，S=4cosθ+6sinθ=2sin（θ+φ）（其中，tanφ=）.

三、動(dòng)態(tài)中與形成的幾何體的體積有關(guān)的問(wèn)題

例3.一個(gè)棱長(zhǎng)為12的正方體形狀的鐵盒內(nèi)放置一個(gè)正四面體，且能使該正四面體在鐵盒內(nèi)任意轉(zhuǎn)動(dòng)，則該正四面體的體積的最大值是______.

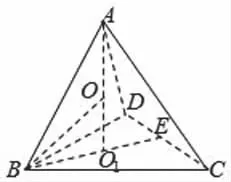
解析：如圖，設(shè)正四面體A-BCD的棱長(zhǎng)為x，過(guò)A作AO1⊥底面BCD于O1，連接BO1并延

設(shè)正四面體A-BCD的外接球的半徑為r，

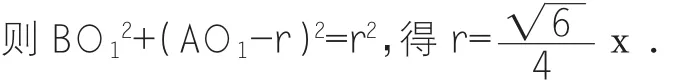
要使正四面體可以在棱長(zhǎng)為12的正方體內(nèi)任意轉(zhuǎn)動(dòng)，

四、動(dòng)態(tài)中與形成的角有關(guān)的問(wèn)題

例 4.在四面體PABC中，PA=PB=PC=AB，如果PA與平面ABC所成的角等于60°，則PC與平面PAB所成的角的最大值是 .

解析：如圖所示，過(guò)點(diǎn)P作PO⊥平面ABC于點(diǎn)O，連接OA，OB，OC.取 AB的中點(diǎn) D，連接OD.則∠PAO是PA與平面ABC所成的角，其大小等于 60°.不妨設(shè) PA=2=AB=PB=PC，則 P O=.因?yàn)镻D=.所以點(diǎn)O與D必然重合. 可知點(diǎn)C在以O(shè)為圓心，AB為直徑的圓周上運(yùn)動(dòng)（去掉A，B兩點(diǎn)）.當(dāng)且僅當(dāng)CD⊥AB時(shí)，PC與平面PAB所成的角取得最大值 30°.

五、動(dòng)態(tài)中形成與球的體積有關(guān)的問(wèn)題

例5.已知A，B是球O的球面上兩點(diǎn)，∠AOB=90°，C為該球面上的動(dòng)點(diǎn)，若三棱錐O-ABC體積的最大值為36，則球O的表面積為

A.36π B.64π

C.144π D.256π

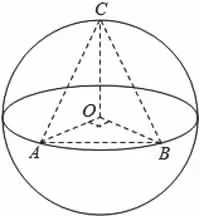
解析：如圖所示，當(dāng)C點(diǎn)位于垂直于面AOB的直徑端點(diǎn)時(shí)，三棱錐O-ABC的體積最大，設(shè)故R=6，則球O的表面積為4πR2，故選：C.

通過(guò)以上例題的分析可知，在立體幾何中由動(dòng)態(tài)引出的有關(guān)距離、面積、體積、角的最值或范圍問(wèn)題，思維難度比較高，對(duì)直觀想象、數(shù)學(xué)推理等核心素養(yǎng)的要求很高，解決問(wèn)題的基本方法有：利用極限位置法，即通過(guò)分析圖形特征，找出取得最值的位置，再進(jìn)行計(jì)算；在動(dòng)中找定，引入變量，構(gòu)建函數(shù)模型，通過(guò)研究函數(shù)的最值解決問(wèn)題。