深“挖”概念 促進理解
——以函數一章為例淺談數學概念教與學

>>>盧艷威

一、問題的產生與解決

1.背景

高一第一學期第一次月考數學試卷中的兩道題：

15.若函數y=f（x+1）的定義域為[-2，4]，則函數y=f（2x-1）的定義域為.

18.已知f（x）是定義域在R上的奇函數，當x＞0時，f（x）=x3+x+1，求f（x）的解析式.

經統(tǒng)計，這兩道題全年級的正答率分別為21.7%和 35%。

2.錯因分析

為了分析錯因，筆者設計以下兩個問題與學生交流：

問題1.f（x+1）和f（2x-1）的定義域分別指的是什么?

問題2.你認為f（x）可以表示哪些意義?

結果，第1個問題只有32%的學生回答正確；第2個問題有63%的學生回答“它指的是以x為自變量的函數”，只有37%的學生回答“它可以指自變量取值為x時的函數值”。

由此不難發(fā)現(xiàn)，在概念的教與學中，對概念的呈現(xiàn)、形成和運用等環(huán)節(jié)缺乏精心設計與必要思考。

3.針對性補償教學

找出了問題，筆者進行了相應的補償性教學。

案例1.針對15題，筆者設計了以下課堂提問：

問題1：函數的定義域指的是什么?你如何理解?

學生回答：函數的定義域指的是函數自變量的取值集合。

教師進一步追問：這啟發(fā)我們求定義域先看什么？

學生：先看自變量是什么。

問題2：函數f（x+1）的自變量是什么?函數f（2x-1）的自變量又是什么?

學生答案不一，少數學生說自變量仍是x，大部 分學生說 f（x+1）的 自 變量是 x+1，f（2x-1）的自變量是 2x-1.

教師啟發(fā)學生舉例說明.

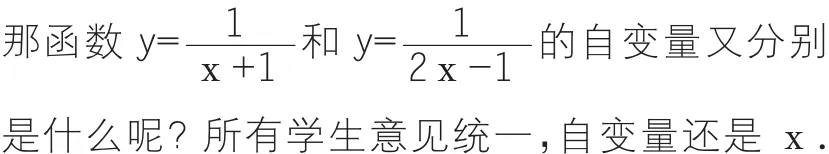
問題3：結合上述例子說明函數y=f（x+1）的定義域與函數y=f（2x-1）的定義域的聯(lián)系是什么?

學生：函數y=f（x+1）中x+1的范圍與y=f（2x-1）中2x-1的范圍一致.

案例2. 針對18題，筆者設計了以下課堂提問：

問題 1：請你依據課本，回答：f（x）的含義有哪些?

學生：f（x）指的是關于x的函數，也表示與x對應的函數值.

問題 2：已知 f（x）是定義在 R 上的奇函數，當 x＞0 時，f（x）=x3+x+1.你能否求解 f（-2）和f（a）（a＜0）?

學生：f（2）=11，f（-2）=-f（2）=-11，

當 a＜0 時，-a＞0，則 f（-a）=-a3+a+1，得f（a）=-f（-a）=a3+a-1.

問題3：當x＜0時，能否求出相應的函數值 f（x）?

學生很容易得出x＜0時，f（x）=x3+x-1，從而順利解答18題.

二、深“挖”概念促理解的策略

1.回歸教材，培養(yǎng)學生提取信息的能力

講授數學概念之前，應適當預設一些問題讓學生獨立思考，并通過閱讀教材促進學生對概念的挖掘，培養(yǎng)其自學能力。在遇到困惑時，引導學生回歸教材，從數學概念本身尋找思維的突破口。如在函數奇偶性的學習中，很多學生在判斷函數奇偶性時容易忽略“定義域對稱”這一必要條件。其原因主要是學生對于定義中“任意一個x”的“任意”二字的理解。若在此處教師能精心設計問題，如“你是如何理解‘任意’的？在判斷函數奇偶性時需要注意什么？”，效果是不言而喻的。

2.創(chuàng)設恰當情境，促進概念理解完整化

一個概念的形成是呈螺旋式上升的，要經過具體到抽象、感性到理性的過程。恰當的情境創(chuàng)設能使概念的形成自然、合理。情境創(chuàng)設是否合理決定于所舉例子能否促進概念理解的完整化。如在函數概念一節(jié)的情境創(chuàng)設中，既要有用解析式表達的函數例子，也要有用圖象和列表表達的函數例子，否則學生容易形成“函數就一個解析式”的錯誤印象。問題情境的創(chuàng)設既要能激發(fā)學生的求知欲，又要能使學生在問題的解決中體會到概念的合理性。如對函數單調性定義中“任意”的理解，若在其中依次設置問題：“存在 x1，x2， 當 a＜x1＜x2＜b時，有 f（a）＜f（x1）＜f（x2）＜f（x3）＜f（b），能保證函數 y=f（x）在區(qū)間[a，b]上遞增嗎？”“存在 x1，x2，x3，當 a＜x1＜x2＜x3＜b 時，有 f（a）＜f（x1）＜f（x2）＜f（x3）＜f（b），能保證函數 y=f（x）在區(qū)間[a，b]上遞增嗎？ ”“你認為n需要如何取值時，當a＜x1＜x2＜x3＜…＜xn＜b，則 f（a）＜f（x1）＜f（x2）＜…＜f（xn）＜f（b） ，才能保證函數 y=f（x）在區(qū)間[a，b]上遞增？ ”

3.恰當類比，使概念理解形象化、直觀化

某些情況下，對于數學中的抽象概念，簡單的推理與闡釋難以奏效。這時，恰當使用類比可以變陌生為熟悉，化抽象為形象，能增加學生對數學的學習興趣，提高學生的觀察能力和概括能力。如關于函數的三要素，學生理解模棱兩可，課堂教學中筆者就將“定義域、對應關系和值域”分別類比于“布料、加工程序和服裝”，學生表現(xiàn)出極大的興趣并容易突破這一難點。

4.正反舉例，突破理解瓶頸

通過舉例理解與鞏固數學概念是教師在教學中常用的手段，教師一方面可以通過自己舉例讓學生突破理解障礙，另一方面也可以讓學生舉例從而獲得相應的反饋。舉例過程中，對正例反例應適當兼顧，而不能一味地只舉正例；在正反例的認知沖突中，適時地引導學生討論，分別表達自己對現(xiàn)象背后原因的思考，在相互啟發(fā)中加深對概念的理解。