可表示一致模的加法生成子

侯曉東，李 鋼

（齊魯工業大學（山東省科學院）數學與統計學院，濟南 250353）

三角模（t-norm）和三角余模（t-conorm）作為重要的合取型和析取型聚合算子[1]，被廣泛應用于模糊控制、模糊聚類、信息聚合和人工智能等領域.Fodor 等[2]提出了一致模（uninorm）的概念，使得三角模和三角余模得以推廣和統一，為相關模糊理論的研究奠定了基礎[3-4].一致模廣泛應用于神經網絡、專家系統、圖像處理和信息融合等領域.文獻[5]綜述了各類一致模的相關結論，并指出其應用領域.本文研究可表示一致模的加法生成子，得到當滿足一定條件時，加法生成子可由給定的一致模構造出來，同時得到了基礎三角模和基礎三角余模的加法生成子，最后給出了所得結論在可表示一致模的序關系以及對應剩余蘊涵方面的應用.本文結論可應用于信息決策、優化控制和模糊邏輯等領域.

1 預備知識

首先給出相關概念.

定義 1[2]對于二元算子 U：[0，1]× [0，1]，若Ax、y、z∈[0，1]，有

（1）U（x，y）=U（y，x）；

（2）U（x，U（y，z））=U（U（x，y），z）；

（3）U（x，y）≤U（x，z），y≤z；

（4）Ee∈[0，1]，使得 U（e，x）=x，Ax∈[0，1].

則稱U 為一致模，其中e 稱為U 的單位元.當e = 1時，U 退化為三角模T；當e =0 時，U 退化為三角余模S.

由一致模U，定義三角模TU和三角余模SU為

TU和SU分別稱為U 的基礎三角模和基礎三角余模[2].

定義2[5]給定一致模U，單位元e∈]0，1[，若存在函數 h（x）：[0，1]→，h（x）是連續的且嚴格遞增的，h（0）=-∞，h（e）=0，h（1）=+∞，使得

U（x，y）=h-1（h（x）+h（y））

其中：（x，y）∈[0，1]2{（0，1），（1，0）}，則稱U 為可表示一致模，稱h（x）為U 的加法生成子.

可表示一致模U 的加法生成子不唯一，若h（x）是 U 的加法生成子，則 kh（x）（k >0）也是 U 的加法生成子.記AU為U 的所有加法生成子構成的集合.

定理1[6]設一致模U 的單位元e∈]0，1[，則U 是幾乎連續的（即U 在（x，y）∈[0，1]2{（0，1），（1，0）}連續）當且僅當U 是可表示一致模.

可表示一致模通常由給定的加法生成子構造.本文討論逆問題，即，給定可表示一致模U，研究如何構造U 的加法生成子.

2 主要結論

下面的定理2 給出了如何利用可表示一致模U構造其加法生成子h（x）.

定理2設U 為可表示一致模，單位元e∈]0，1[.若加法生成子h（x）在]0，1]存在連續導數，且滿足

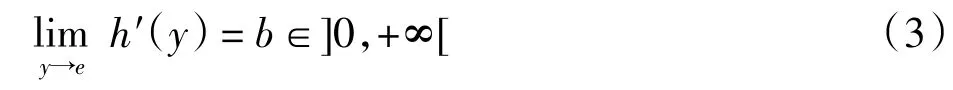
則 h（x）可表示為：

證明（1）由于 h（x）在]0，1]存在連續導數，則h（x）的連續性顯然.

（4）由反函數的導數公式[7]可得

所以有

綜上定理得證.

下面給出可表示一致模U 的基礎三角模和基礎三角余模的加法生成子.

推論1設U 為可表示一致模，單位元e∈]0，1[，則有

（1）U 的基礎三角模TU的加法生成子為

（2）U 的基礎三角余模SU的加法生成子為

證明（1）當 x≤e 時則有

命題設U 為可表示一致模，單位元e∈]0，1[.若存在一致模U 的一個加法生成子h（x）∈AU滿足則AU中任意加法生成子k（x）均滿足

證明設加法生成子h（x）∈AU，則對于任意加法生成子 k（x）∈AU，存在 q >0，使得 k（x）=h（x）·q[2]，因為則有

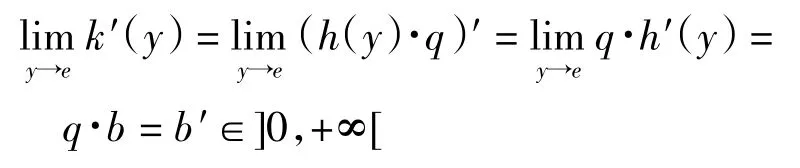
由定理2 和命題可得到如下推論2.

推論2設U 為可表示一致模，單位元e∈]0，1[，其加法生成子在]0，1]存在連續導數.若存在加法生成子也是一致模U 的加法生成子，其表達式為

例1設一致模U 的表達式為

當k > 0 時，kh*（x）仍是U 的加法生成子，4h*（x）=即為文獻[2]中的算例.

注：若定理2 中的式（3）不成立，則無法用式（4）或式（5）構造加法生成子.

例 2若一致模 U 可由加法生成子h（x）構造，h（x）具有表達式

3 應用

下面給出定理2 在討論可表示一致模的序關系以及對應剩余蘊涵方面的應用.

定理3[8]設U1和U2為單位元相同的可表示一致模，則 U1≤U2→h1h2-1是超可加的，其中 h1、h2分別為 U1、U2的加法生成子.

例3給定一致模

由定理1 可知U1和U2均為可表示一致模.由推論2可計算得到U1和U2的加法生成子分別為

由文獻[9]的定理7 知可表示一致模誘導的剩余蘊涵可通過加法生成子表示為

利用推論2 可以直接寫出例3 中的U1誘導的剩余蘊涵，當（x，y）∈[0，1]2{（0，0），（1，1）}時，

當（x，y）∈{（0，0），（1，1）}時，φμ（x，y）=1.