基于分簇的雙簇首水下傳感器網絡時間同步算法

孔維全,劉廣鐘

(上海海事大學 信息工程學院,上海 201306)

0 概述

近年來,水下傳感器網絡受到學術界和工業界研究人員的極大關注[1],該網絡可應用于沿海監視、環境監測、海底勘探、防災偵查等大量應用場景。然而,由于陸地傳感器常用的無線電波在水下會產生高衰減,因此聲學通信成為水下傳感器主要的傳輸方法。

為了通過節點間的協調與合作完成各項分布式任務,需要時間同步技術作為支撐,時間同步技術是時分復用調度、傳感數據融合、介質訪問控制協議等多項關鍵技術的基礎[2]。然而,水下傳感器的節點部署要求較高,一旦部署完成很難進行維護和更換,所以傳感器的計算資源與能量存儲都非常有限。此外,水聲信道的傳播速度大約為1 500 m/s,比電磁波信號低 5個數量級,由于陸地傳感器在進行時間同步時通常會忽略傳播延遲,而在水下環境中,巨大的傳播延遲在節點通信時是不可忽略的重要因素,其受海水的溫度、鹽度、密度等多種因素的影響,因此水下聲波的速度會發生隨機性較大的變化。同時,傳感器節點具有隨洋流影響而移動的特點,在某節點發送消息和收到回復消息的時間間隔內,節點會發生相對移動,導致傳播延遲在每次信息交互中都會發生變化[3],更重要的是,水下傳感器的計算能力有限,因此,不宜設計過于復雜的算法使其消耗大量能量。

本文綜合考慮水下通信的特點,提出一種基于低能耗分簇輔助的雙簇首時間同步算法DCH-Sync。采用分簇模型求解在能耗最低情況下的最佳分簇數量,從簇中選取2個最優節點作為主簇首和副簇首,通過移動信標節點完成簇首同步,并引入節點移動模型提高定位精度。在此基礎上,利用雙簇首完成對普通節點的時間同步。

1 相關工作

目前,針對陸地傳感器網絡的時間同步算法的研究已取得較多成果,例如,RBS(Reference Broadcast Synchronization)算法[4]使用第三方發送廣播報文實現全局同步,TPSN(Timing-sync Protocol for Sensor Network)算法[5]對所有節點進行分層和逐層同步,FTSP(Flooding Time Synchronization Protocol)算法[6]則考慮了根節點選舉與節點失效等的影響。然而,上述研究均未考慮海洋環境的特殊性,并且忽略了傳播延遲的影響,因此這類協議不適用于水下傳感器。

近年來,針對水下傳感器時間同步的研究已取得了一些進展。高延遲水下時間同步協議(Time Synchronization for High Latency,TSHL)[7]將時間同步分為2個階段,在第1階段,待同步節點通過接收信標節點發送的25個消息包,利用線性擬合估計自身的時鐘頻偏,在第2階段,待同步節點與信標節點進行雙向交互,從而計算出時鐘相偏。然而,該算法未考慮節點移動的問題,且假設傳播延遲不變,并不適用于實際情況。MU-Sync是針對水下節點移動性提出的一種具有代表性的同步算法[8],該算法運用分簇思想進行兩輪線性擬合。第1輪采用發送-接收的方式進行10次信息包交互,每次交互可稱為一次REF包交換,該輪線性擬合忽略傳播延遲的變化,采用固定值計算各節點的時鐘頻偏,而第2輪線性擬合去除相應的傳播延遲,得到更加精確的時鐘偏移估計。Mobi-Sync[9]引入節點移動模型,并使用3個信標節點對一個節點進行同步,通過一組速度矢量描述節點的運動情況,但此算法過于繁瑣且能耗較大,難以實現。D-Sync[10]算法利用多普勒效應輔助時間同步,通過比較發送、接收數據包的時間估計多普勒因子的值,獲得節點的移動方向與速度,其缺點在于需要配備額外的多普勒測量器,增加了部署成本。文獻[11]提出一種多普勒輔助水下傳感器網絡時間同步機制,由于節點在數據傳輸時發生運動,數據幀在多普勒頻移的影響下會被壓縮或擴展,因此接收信號的長度會發生變化,利用這一特性可計算多普勒因子,從而完成時間同步。但是,該方法實現難度過高且需要額外的硬件才能完成,不適用于實際情況。上述水下傳感器時間同步算法雖然考慮了水下高延遲和節點移動等因素,但均未解決節點能耗過大的問題,具有一定的局限性。本文綜合考慮水下通信的特點,通過分簇模型解決各節點的能耗問題[12]。

2 低能耗分簇技術

對于水下傳感器網絡,其節點分簇模型已有較多研究,當前多數分簇算法采用“一對多”的數據傳輸模式,容易增加網絡節點的通信負載,且能量消耗不均衡。由于在水下環境部署節點較困難,一旦簇首節點的能量消耗完畢,就必須重建網絡,這對系統的穩定性和安全性造成極大的影響,因此需要考慮冗余機制。

本文在分簇過程中選取雙簇首,一方面是為了在主簇首無法工作時,副簇首能接替其位置,另一方面,在后續過程中,使用雙簇首輔助普通節點進行同步,可有效提高同步精度。圖1給出分簇后節點的工作過程,其中傳感器網絡的結構主要由信標節點、主簇首、副簇首和成員節點組成。該分簇模型主要用于時間同步而非數據傳輸工作,信標節點首先對主、副簇首進行時間同步,再利用簇首同步成員節點。無論是簇首與信標的通信還是簇內通信一律采用單跳通信方式而非通過路由多跳存儲轉發,避免靠近信標的節點因能量消耗過度而迅速消亡。

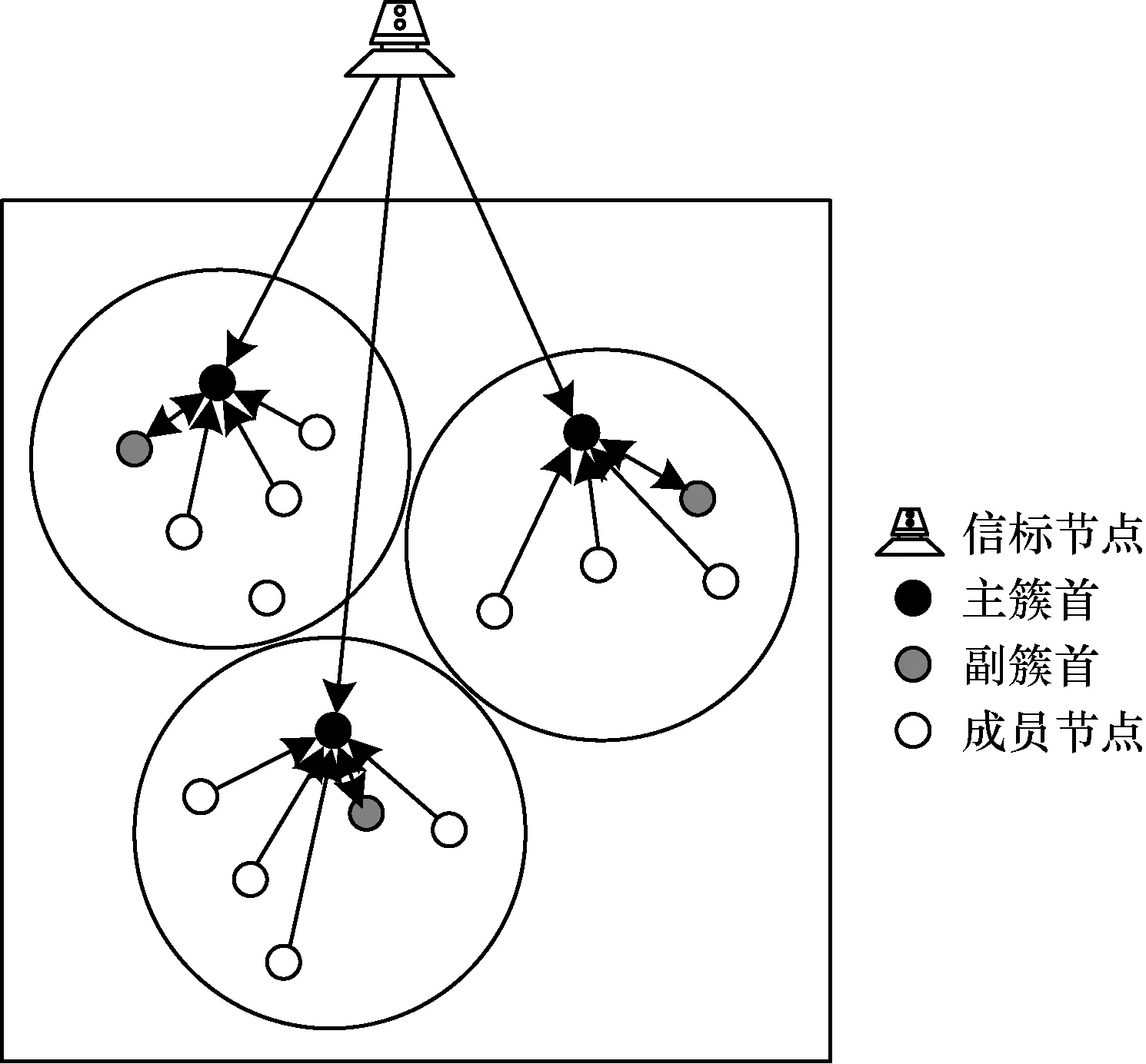
圖1 分簇后節點的工作過程

與傳統的傳感器不同,水下傳感器的能量消耗與距離、頻率和深度等因素相關。本文采用文獻[13]的水聲能耗模型,當發射機傳輸大小為lbit的數據包時,其消耗的能量如式(1)所示。

ETX(l,d)=lEelec+lTbCHdea(f)d

(1)

其中,Eelec是節點處理1 bit信息所消耗的能量,Tb是發送1 bit信息所需的時間,C=2π×0.67×10-9.5,H為節點的深度,d為傳輸距離,a(f)是吸收系數,其計算公式如下:

(2)

其中,f表示頻率,單位為kHz,a(f)單位為dB/km。式(2)體現了信號頻率與能量衰減之間的關系。

接收機接收lbit的數據包與數據融合所消耗的能量相同,如式(3)所示。

ERX(l,d)=lEelec

(3)

文獻[14]提出最佳分簇數量的計算方法,但其未考慮簇首與成員節點工作方式不同而導致的能量消耗差異。本文對該方法進行改進,假設在求最佳分簇數量期望值時不考慮簇內節點的轉發任務,單純從簇首和成員節點發送、接收和數據融合消耗能量的角度進行分析。

從成員節點的角度來看,第k個簇的第i個成員節點發送1 bit信息需要的能量如下:

EM-TX(ki)=Eelec+TbCHrea(f)r

(4)

其中,r表示節點至簇首的距離。

接收1 bit信息需要的能量是:

EM-RX(ki)=Eelec

(5)

成員節點所消耗的總能量如式(6)所示。

EM-total(ki)=2Eelec+TbCHrea(f)r

(6)

從簇首節點的角度來看,其消耗的能量由發送數據、接收成員節點數據和數據融合3個步驟所需的能量組成,如式(7)所示。

EC-total(k)=2NkEelec+Nk(Eelec+TbCHrea(f)r)

(7)

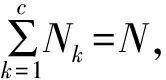
(8)

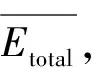
(9)

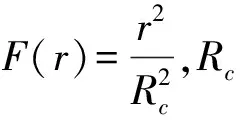
(10)

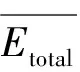
在完成分簇以后,需在每個簇中選出主簇首與副簇首。首先引入網絡平均能量Ea(i),在進行簇首選舉前,只有剩余能量高于網絡平均能量的節點(Er(i)≥Ea(i))才有資格參與選舉,其目的是防止能量過低的節點被選舉為簇首,從而平衡整個網絡的能量消耗。然后通過式(11)計算每個節點的綜合屬性值W(i),選取出屬性值最高和次高的節點作為主簇首與副簇首。

(11)

其中,Ei(i)和Er(i)分別是節點i的初始能量和剩余能量,Ea(i)是節點i所在簇的平均能量,D是節點距離水面的深度,ω1、ω2是在競選過程中能量因素與節點深度的比例,且ω1+ω2=1。通過式(11)可以選舉出剩余能量高且深度較淺的節點作為簇首節點。

3 簇首同步

簇首是簇中唯一與外界通信的節點,其不僅需要獲得高精度的時間信息,而且負責簇內全部節點的時間同步工作,具有非常重要的作用。本節主要解決簇首節點的時間同步問題。在文獻[15]中,簇首節點直接向水面浮標發出同步請求,但未考慮某些簇首所處位置過深的情況,導致傳播距離過遠,影響同步精度。文獻[16]通過多跳傳輸方法進行同步,但每個中間節點在處理數據包時都會產生一定的時延,經過多跳累積后會造成更大的延遲。文獻[17]使用移動信標節點對所有節點進行時間同步,本文在其基礎上進行改進,采用單跳傳輸模式以減少因數據包多跳傳輸而產生的延遲與同步誤差。將自主式水下交通工具(Autonomous Underwater Vehicle,AUV)作為信標節點,對所有簇中的主簇首與副簇首直接進行時間同步。由于AUV能量充足且具有高效移動性,因此不會出現能量不足的情況。考慮到節點的移動對傳播延遲產生的影響,本文選取權威的洋流模型模擬節點的移動方式,并計算移動速率。具體的報文交互采用基于發送-接收的單向與雙向混合報文同步方式,其中,單向交互用于計算時鐘頻偏,雙向交互用于計算時鐘相偏。

AUV在進行時間同步時應盡可能接近每一個待同步簇首,以減少聲速變化帶來的影響,同時應將運動軌跡設計得盡可能簡單、高效。AUV的運動軌跡如圖2所示,圖中實線為AUV進行同步工作時的主運動軌跡,負責當前層次中各簇首節點的同步工作,保證各節點在AUV通信半徑之內,虛線是輔助運動軌跡,幫助AUV潛入更深水域,實現深層次的簇首節點同步工作。以此循環,直至完成所有節點的同步。

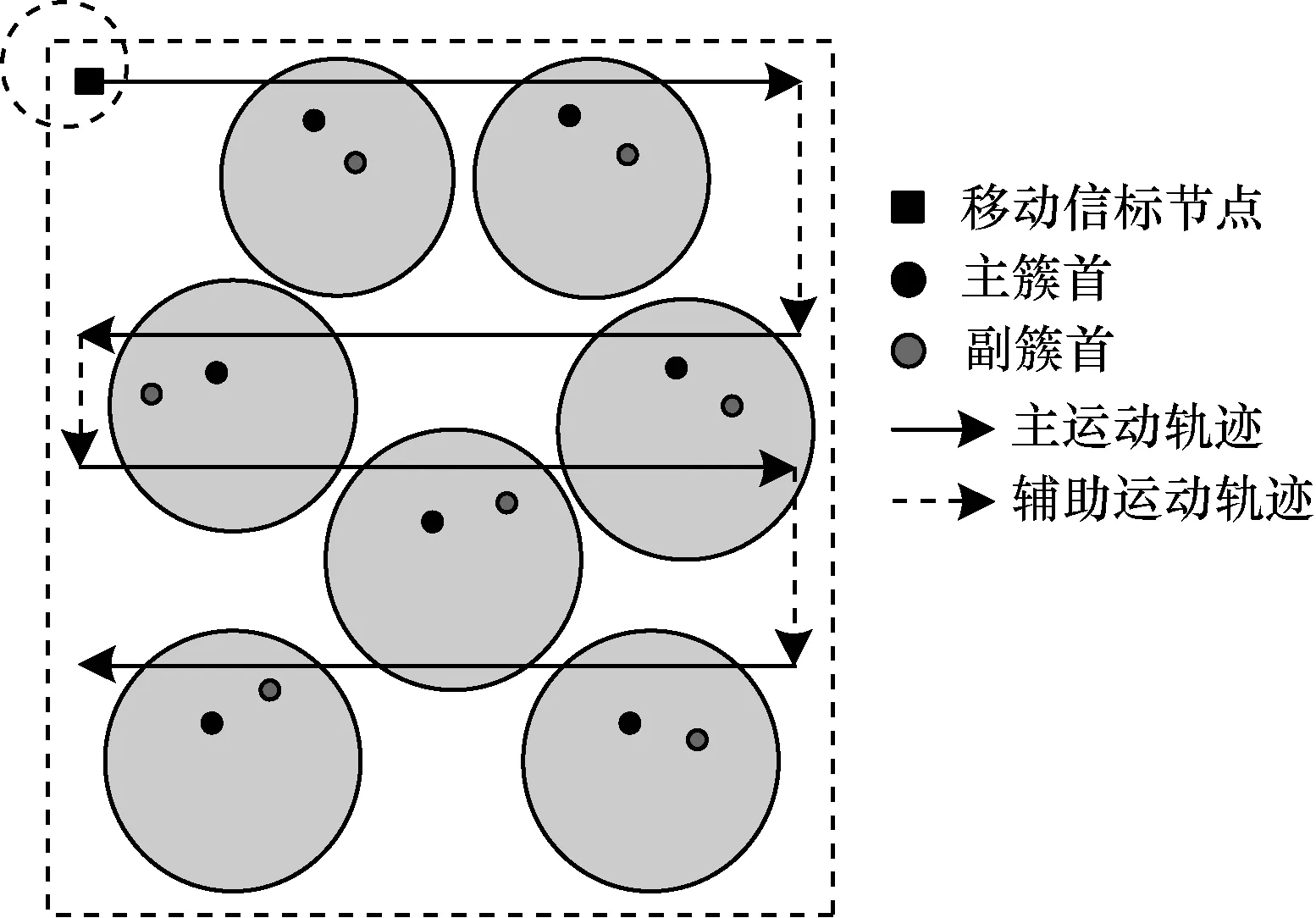
圖2 移動信標節點移動軌跡

在同步過程中引入水下節點移動模型,由于節點的移動會造成兩節點的相對位置發生變化,因此傳播延遲會有所不同,需要考慮節點移動速度對同步過程的影響。文獻[18]提出一個權威洋流模型,如式(12)所示。

(12)

其中,c用來控制洋流位移速率,B(t)用來控制曲線的寬度,ε用來控制整個洋流場的振幅,ω是洋流場中洋流通過的頻率,相關參數按經驗進行取值,具體如下:A=1.2,c=0.12,ω=0.4,ε=0.3,k=2π/7.5。在一般情況下,僅考慮節點在x和y方向的位移,不考慮豎直方向上的位移,則節點在x和y方向上的運動速度如下:

(13)

圖3給出詳細的同步示意圖。根據時鐘同步原理,普通節點C的本地時鐘與標準時鐘的關系為T=λt+β,其中,t代表標準時間,λ代表時鐘頻偏,β代表時鐘相偏[19]。

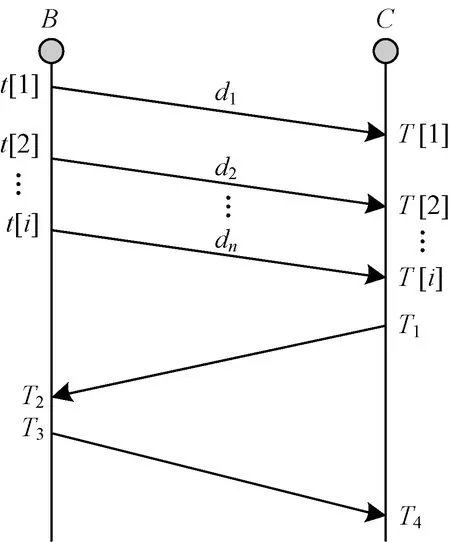
圖3 信標節點與簇首的報文交互

Fig.3 Message interactions between beacon nodes and cluster heads

簇首同步的過程分為如下2個階段:

1)第1階段用于計算時鐘頻偏,信標節點B連續發送i個同步信息數據包給簇首節點C,其中,di是數據傳輸延遲,t[i]代表信標節點發送第i個數據包的時間戳,T[i]代表簇首節點接收第i個數據包的時間戳,其相互關系如式(14)所示。本文規定信標節點共發送10個數據包。

t[i]+di=λT[i]+β

(14)

定義Si是簇首C第i次接收到數據包時與信標節點的距離,則Si與Si-1之間有如下關系:

Si=Si-1+v(t[i]-λT[i-1]-β)+v(λT[i]+β-t[i])

(15)

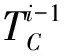
(16)

其中,c是水下聲速。由于此時信標節點與簇首距離較近,因此可忽略聲速的變化,設定c=1 500 m/s,則可算出每個數據包的傳輸延遲,如式(17)所示。

(17)

其中,v是節點在水下的移動速度,ΔT[i]的計算公式如下:

(18)

聯立式(11)、式(12),整理后可得式(19)。

(19)

由此可計算出節點的時鐘頻偏。

2)第2階段通過發送-接收模式交互數據包。簇首首先在T1時刻發送信息,信標節點在T2時刻接收到數據包,隨后在T3時刻發送反饋數據包,簇首在T4時刻接收。時鐘相偏可以通過式(20)～式(22)進行計算。

T1+D=λT2+β

(20)

T3+D=λT4+β

(21)

(22)

4 簇內節點同步

在主簇首與副簇首完成時間同步以后,其可充當簇內的信標節點,向各成員節點發送時間同步消息。文獻[3]提出使用3個信標節點完成對一個普通節點的時間同步,并使用一組速度矢量來表示節點的運動速度,從而推算出節點的傳播延遲。然而,該算法復雜度高,不適用于實際情況。本文使用主簇首與副簇首2個節點對普通節點進行同步。在正常工作時,2個簇首同時進行時間同步工作,若主簇首或副簇首出現故障,則使用單個簇首進行同步。此方法與單信標時間同步相比,雖然會增加一部分能量消耗,但提高了同步精度,并且系統的冗余性和魯棒性也得到增強。由于水下情況復雜,因此需考慮聲速的變化,根據深度、溫度等因素計算實時的聲速值。報文交互采用基于發送-接收的單向與雙向混合報文同步方式,并結合聲速與節點移動速度計算時鐘頻偏和相偏。

在水下傳感器網絡中,時間同步的精度受到各種因素的影響,其與陸地傳感器最大的不同在于,水下傳感器具有較高的傳播延遲,而傳播延遲與聲速密切相關。陸地傳感器的傳播介質是空氣,一般可忽略傳播延遲,而在海洋環境中,聲波的傳播速度會受到深度、溫度和鹽度等各種因素的影響[19],因此在設計時間同步算法時需考慮聲速的變化。目前,較常使用的衡量聲速的方法如式(23)所示[20-21]。

c(t,s,p)=1 449.2+4.6t-0.55t2+0.000 29t3+

(1.34-0.01t)(s-35)+0.16p

(23)

其中,c為聲速,t、s和p分別表示溫度、鹽度和壓力。

圖4給出簇內各節點在進行時間同步時的信息交換過程,圖5為普通節點與簇首節點之間的報文發送過程。由圖5可知,同步進程由普通節點A發起,分別向兩個簇首S1、S2(即主簇首和副簇首)發送同步請求報文RTS,其中包含MAC層時間戳T[1]。在收到RTS之后,簇首記錄本地時間t[1]并開始向普通節點A連續發送i=5個回復包CTS[i],2個包之間的間隔時間固定。報文CTS[i]中包含MAC層時間戳t[i]、溫度tSi和壓力pSi。普通節點收到CTS[i]后,記錄其本地時間戳T[i],同時記錄接收時刻溫度tAi和壓力pAi。假設每個節點的深度已知,則可用式(19)和式(20)計算出溫度和壓力值。隨后,普通節點分別對所接收到的報文中的溫度、壓力等數據取均值,并代入式(21)中計算聲速。

圖4 簇內時間同步時的信息交換過程

Fig.4 Information exchange process during time synchroni-zation within a cluster

圖5 簇內報文發送過程

在同步過程中,各時間戳之間的關系可用式(24)和式(25)表示。

λT[1]+β+d1=t[1]

(24)

t[i]+di=λT[i]+β,i>1

(25)

時鐘頻偏λ可用第2節提到的方法進行求解,如式(26)所示。

(26)

其中,聲速c由普通節點在數據包交互過程中獲取的信息計算得出,節點的移動速度v根據洋流模型進行計算,時鐘相偏可根據式(22)計算得到。

5 仿真結果與分析

本文采用Matlab進行仿真,并在相同環境下比較本文算法與DCH-Sync、TSHL、MU-Sync、multi-hop、D-Sync等算法的性能差異。本文的仿真在1 000 m×1 000 m的水下環境中進行,其中有100個隨機分布的傳感器節點,節點運動采用隨機洋流模型,仿真中使用的時間戳為MAC層時間戳,其他仿真參數如表1所示。

表1 默認參數值

節點消耗的能量主要取決于產生數據包的數量與報文長度,圖6給出TSHL算法、MU-Sync算法與本文DCH-Sync算法在運行30次同步后產生的數據包數量,以此分析能耗高低。在仿真過程中,假定TSHL算法采用25個成對時元組,MU-Sync算法采用10次REF包交換。從圖6可以看出,本文算法所產生的數據包數量少于其他2種算法,分別比TSHL算法和MU-Sync算法減少62.89%和28.95%,其原因是TSHL算法和MU-Sync算法需要進行多次線性擬合,導致數據包的開銷增大。

圖6 同步次數與數據包數量的關系

Fig.6 Relationship between the number of synchronization times and number of data packets

此外,本文研究了如何有效進行簇首間的時間同步。若簇首直接與水面浮標進行同步,一些距離水面較遠的節點需要多跳傳輸才能與信標進行通信,從而產生傳輸延遲,大幅影響同步精度,因此,本文采用AUV作為移動信標輔助同步工作。圖7給出本文算法與多跳傳輸算法在同步完成后,本地時鐘誤差的增長趨勢,可以看出,本文算法的誤差明顯小于多跳傳輸算法,在105s以后,誤差減小52.57%左右,在106s以后,誤差約減小35.60%。

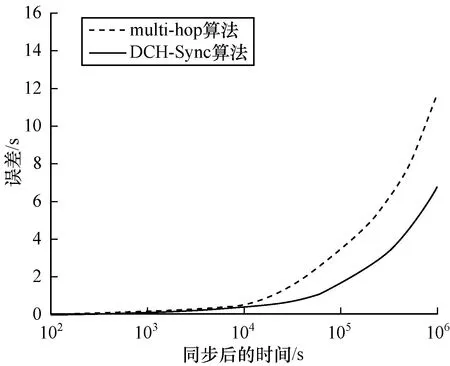
圖7 簇首時間同步后的本地時鐘誤差變化趨勢對比

Fig.7 Comparison of the varying trends of local clock errors after time synchronization between cluster heads

圖8給出本文算法、MU-Sync算法和TSHL算法在完成同步后,本地時鐘誤差的增長趨勢。從圖8可以看出,本文算法的誤差明顯小于其他算法,在105s以后,本文算法的誤差分別比TSHL算法、MU-Sync算法降低68.27%和42.80%,在106s以后,分別降低44.56%和18.50%。本文算法的同步誤差之所以小于其他2種算法,主要有2個原因:通過2個節點輔助同一節點的思想,大幅提高了同步精度;采用洋流模型測算節點的速度,提高了傳播延遲的計算精度。

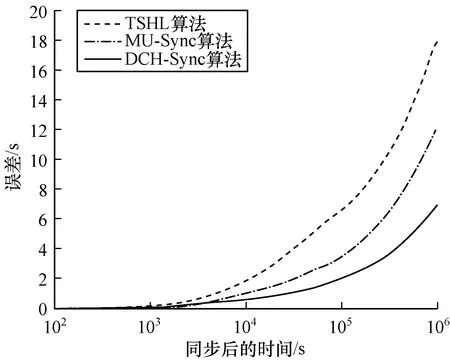
圖8 簇內時間同步后的本地時鐘誤差變化趨勢對比

Fig.8 Comparison of the varying trends of local clock errors after time synchronization within the cluster

傳播延遲的動態變化主要是由節點的移動速度引起的。圖9給出節點的移動速度對同步誤差的影響,將本文算法與同樣考慮節點移動性的MU-Sync算法、D-Sync算法進行對比,速度的變化范圍是1 m/s～4.5 m/s。從圖9可以看出,三者的同步精度基本不受速度變化的影響,但是,MU-Sync算法、D-Sync算法和DCH-Sync算法的同步誤差分別約為0.023 s、0.011 s和0.004 s,本文算法誤差小于其他2種算法。

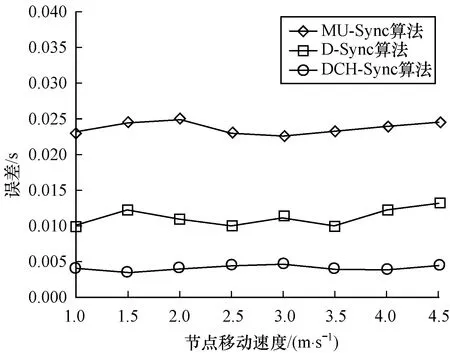
圖9 節點移動速度對同步誤差的影響

Fig.9 Influence of the speed of moving nodes on synchroni-zation errors

6 結束語

本文提出一種基于分簇的雙簇首輔助時間同步算法DCH-Sync。采用分簇模型對節點進行分簇,從簇中選取2個最優節點作為主副簇首,通過節點移動模型完成簇首同步,在此基礎上,利用雙簇首實現對簇內普通節點的同步。仿真結果表明,與TSHL、MU-Sync、multi-hop、D-Sync算法相比,該算法的同步精度較高且能量消耗較少。下一步將優化分簇模型,擴大DCH-Sync算法的應用范圍。