不確定需求下快遞配送網絡魯棒優化

許闖來，胡堅堃，黃有方

上海海事大學 物流科學與工程研究院，上海201306

1 引言

隨著我國經濟的穩步發展，互聯網消費環境的日益成熟和企業信息化的完善，進一步推進了互聯網消費方式的普及。來自國家郵政局公布的數據[1]顯示：2017年“雙11”當天，主要電商企業全天共產生快遞物流訂單8.5億件，同比增長29.4%；全天各郵政、快遞企業共處理3.31億件，同比增長31.5%。電子商務在不同消費群體中的普及為快遞行業帶來了巨大的發展商機，同時也要求城市配送活動在服務能力上更高效，低成本、準時性地滿足多樣化的物流需求。目前我國快遞企業發展水平參差不齊，都面臨著專業化程度低，資源配置不均等問題[2]。近幾年“雙十一購物節”所引發的快遞“爆倉”事件，使得物流配送系統承載著巨大的壓力[3]。快遞需求的集中爆發直接表現為快件量的倍數增長，大量快件堆積在分撥中心[4]。為解決這個問題，快遞公司為分撥中心招聘了大量外包人員以及部分職能崗位的員工。該方法雖然可以幫助提升分撥中心的裝卸效率，但是并不能有效解決貨物積壓的問題，相反會加劇分撥中心的運作壓力。因此合理并有效地規劃配送車輛路徑是避免“快遞變慢遞”的根本之法，也是公司控制人力投入成本，確保客戶按時收貨，提升客戶滿意度和品牌競爭力的重要保障。

車輛路徑問題來源于交通運輸，最早是由Dantzig和Ramser[5]于1959年提出。它是指一定數量的客戶，各自有不同的貨物需求，在一定的約束下，配送中心安排車隊并設計一套運輸路線，滿足貨物在客戶點的運輸[6]。車輛路徑優化是一個NP難問題，可選車輛路徑隨著客戶數量的增加而呈現階乘般的增長。對于一個有15個頂點的VRP問題，其可行解的數目將達到1 012個[7]。現有的快遞分撥物流網絡設計主要針對確定性需求基礎上對分撥網路的構建，容易受到客戶點運輸需求劇烈變動的影響[8-9]。Baldacci等[10]回顧了有容量約束進行VRP精確算法的發展，并對它們的計算性能進行比較。張濤等[11]將熱軋生產批量計劃歸結為不確定車輛數的車輛路徑問題，并用遺傳算法和禁忌搜索算法相結合的混合算法對問題進行求解。

在不確定車輛路徑問題上，研究人員大多采用隨機規劃或者模糊規劃的方法。戎麗霞[12]針對具有不確定需求的車輛路徑問題，建立了基于模糊可信性理論的模糊機會約束規劃模型，利用基于模糊模擬的混合遺傳算法進行求解。邢占文[13]以啟發式算法為基礎，提出了勘探搜索算法和基于非精確距離矩陣的共軛優化算法求解呼和浩特市內帶有顧客需求不確定性和車速度不確定的車輛路徑問題。Chung[14]等運用魯棒優化方法解決結合交通動態性和需求不確定性的網絡設計問題。Yu[15]應用魯棒優化模型處理隨機物流問題，并設計了求解方法。該文建立魯棒線性規劃模型，并通過對比該解與對應確定性模型的解來描述模型的魯棒性。孫華[16]用魯棒優化的方法求解了應急管理下需求和旅行時間不確定的車輛路徑問題。伍方凌[17]首先建立了確定性帶時間窗的班輪支線網絡優化模型，并在此基礎上提出集裝箱班輪支線網絡魯棒優化模型對不確定條件下船舶的運輸航線進行優化選擇。管峰等[18]采用魯棒優化模型解決需求不確定的、有容量限制的車輛路徑問題，證明雖然魯棒優化模型的最優目標函數值較大，但能有效保證路徑在需求波動下的可行性。2017年，熊瑞琦等[19]針對危險貨物配送路徑對不確定因素敏感度較高的問題，提出了魯棒性可調的多配送中心危險貨物配送路徑魯棒優化方法。本文通過引入基于情景集的魯棒優化模型，先對物流分撥網絡結構進行經濟性分析，并與運輸時效優先下的成本進行比較，分析兩種選擇下的成本和總旅行時間差異；將車輛數，旅行時間和成本最低作為模型的3個因變量，通過改進蟻群算法，并用Matlab求解模型，給出決策方案，減緩由于需求波動而帶來的不利影響，為快遞企業選擇合適的分撥路徑提供解決方案。

2 快遞配送物流網絡魯棒優化模型的建立

2.1 問題描述

本文不考慮分撥中心的裝貨時間。快遞企業的VRP模型通常考慮一個配送中心同時服務多個需求客戶點的情況：每個客戶點的位置已知，配送中心有足夠可使用的配送車輛，且每輛車的裝載容量一定；每個客戶只能被服務一次；每條線路上的客戶需求不能超過車輛的最大裝載容量；客戶需求量超出車輛額定容量的限制，得不到運輸的部分給予懲罰。完成配送任務的車輛最終返回配送中心。本文模型求解的目標函數是總成本最小，基于確定需求利用魯棒優化的思想，對物流配送網絡進行設計和優化，同時利用不同的情景集來描述需求的不確定性問題。

2.2 模型建立

本文是由一個配送中心向多個客戶點進行配送。首先建立確定需求下的以成本最低為目標函數的確定性模型，然后在此基礎上建立關于需求量的魯棒性模型。

設車輛路徑網絡圖為G(V,A)，其中V={v0,v1,…,vn}為頂點集合；集合A={(Vi,Vj):i≠j∧i,j∈V}為弧集合；定義v0為配送中心；v1～n為需求客戶點；K為自有同質車輛數目；D為外包同質車輛數目；N={0,1,2,…,n}表示配送中心和客戶點集合；QV為車輛的裝載容量；gi為各客戶點的需求量，且滿足gi≤QV；dij為客戶點i和j之間的距離；tij為客戶點i和j之間的行駛時間；Cf為單位體積燃料成本；Cd為單位裝卸成本；C1為自有車輛固定費用；C2為外包車輛固定費用；ρ為配送車輛單位油耗；[ai,bi]為客戶點i指定的服務時間窗；Nc為完成一個配送班次所用的自有車輛的數量；Nd為完成一個配送班次所用的外包車輛的數量；Xijk為當車輛K經過客戶i到達客戶j時為1，否則為0；yk為當車輛K被使用時為1，否則為0。

2.3 需求不確定下的快遞配送路徑模型

魯棒優化模型是以確定性需求模型為基礎，所以首先建立確定性需求下快遞配送物流網絡模型。

確定性需求的車輛路徑問題模型為：

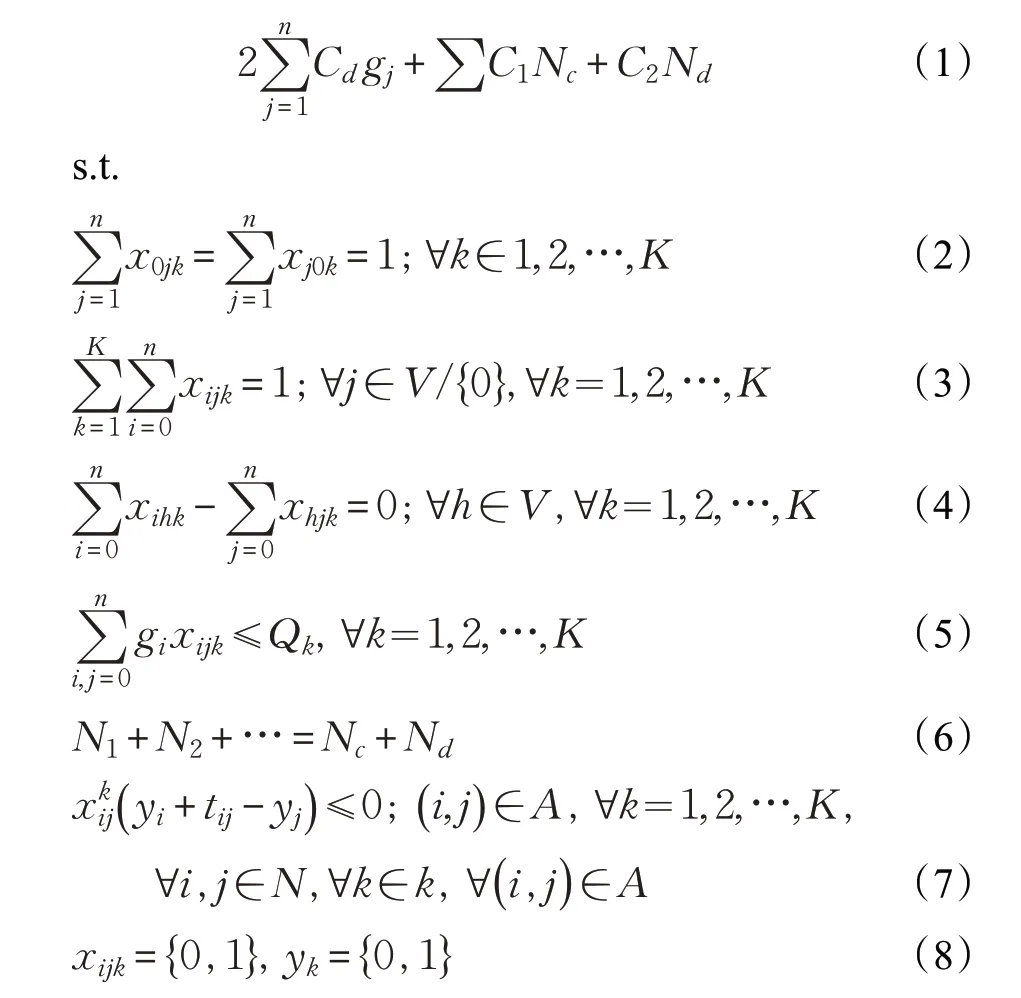
其中，式（1）為成本最小的目標函數，包括司機工資、燃油費用、裝卸成本和車輛固定成本；式（2）表示所有提供服務的車輛都必須從配送中心出發，并最終返回到配送中心；式（3）表示每個客戶點有且只有一輛車到達和服務；式（4）表示抵達客戶的車同時也是離開客戶的車；式（5）約束了車輛的最大載荷；式（6）中，等式左邊表示路徑中投入使用的車輛總數，是自有車輛數和外包車輛數之和；式（7）表示車輛在兩個客戶點之間的行駛要保持連續性；式（8）為參數變量的約束值。

為了更好地研究各客戶需求量不確定的情況，現將魯棒優化的思想運用到快遞配送網絡的設計問題中。假設存在S個需求情景，每個需求情景中含有不確定需求d，每種情景發生的概率對應為ps，對應情景S下客戶j的需求量為

基于情景集s下的魯棒優化模型的目標函數為：

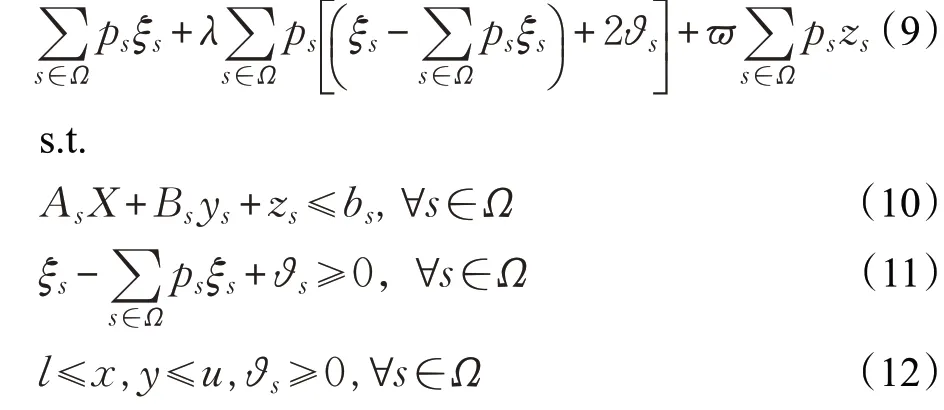
其中，式（9）是基于情景集的魯棒優化的目標函數原型，第一部分考慮了偏離均值的情況，第二部分通過加入λ倍偏差以體現決策者的風險偏好，第三部分為懲罰函數；約束式（10）～（12）保證了得出的魯棒最優解能滿足所有情景。

現將確定性需求下的快遞配送路徑模型加入到基于情景集S下的魯棒優化模型，最終目標函數模型為：

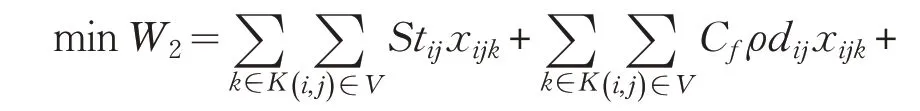
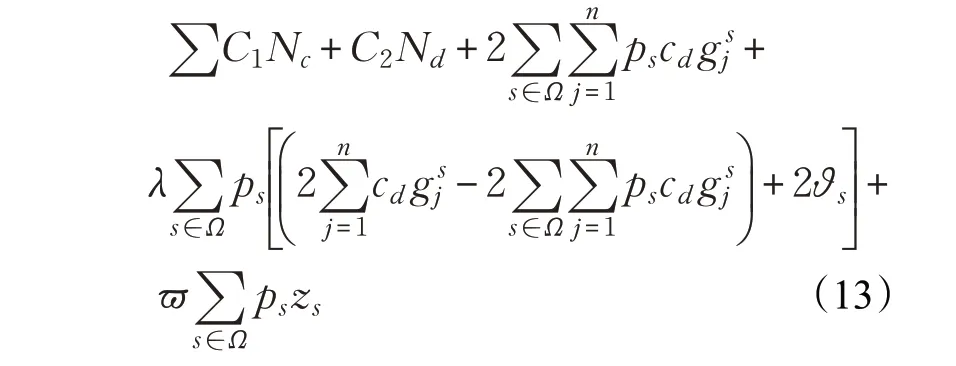
修改和新添加的約束條件：

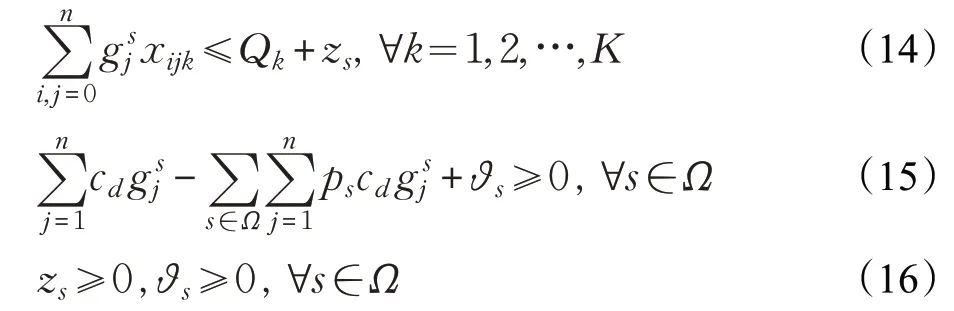
其中，式（13）表示任意情景S下魯棒優化的目標函數，即將公式（9）中的ξs替換成公式（1）中的，其余部分保持不變；式（14）松弛了確定性模型中車輛最大載荷量的約束，允許運輸需求大于車輛最大載荷量，且兩者之間存在偏差zs，即如果客戶點i→j實際需求量小于或等于車輛的最大載荷量，則zs=0，否則zs=，表示存在運輸量為zs的需求得不到滿足，這部分通過式（13）的最后一部分進行懲罰；約束式（15）與基于情景集的魯棒優化模型中約束式（11）相對應，表示解的魯棒性，即對任意情景中的參數值，模型的解都“接近”最優；式（16）為對新添加參數變量的約束。

3 算法設計

本文通過構建不確定需求的魯棒模型，并與確定需求下的模型結果進行比較。蟻群算法適用于求解規模較大的組合優化問題。同時為了避免陷入局部最優，采用2-opt進行局部搜索優化，易于尋找到全局最優解。

采用文獻[20]基礎建立的蟻群算法，算法步驟如下。

步驟1系統初始化：初始化距離dij，設置迭代次數iter_max=200，Q=20為環境初始殘留信息素。

步驟2初始化m只螞蟻，將n個客戶點放入螞蟻的未訪問城市表notVisitk，客戶點需求量qk。

步驟3螞蟻k隨機選一個客戶點放入螞蟻路徑solutionk，同時從notVisitk將該客戶點刪除。

步驟4根據公式

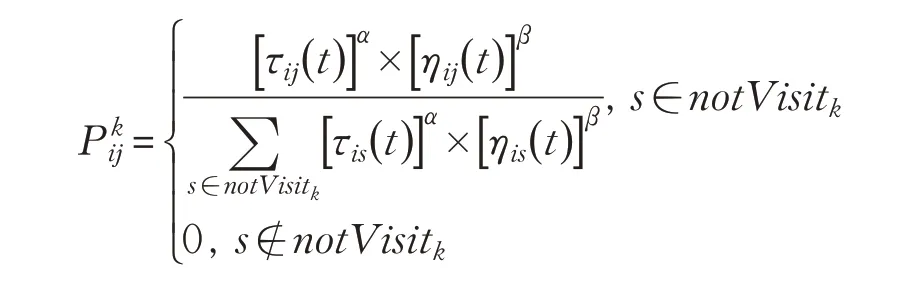
計算螞蟻從客戶點i轉移到客戶點j的轉移概率。

步驟5如果notVisitk不為空，則用輪盤賭法隨機選擇一個客戶點放入solutionk，同時從notVisitk將該客戶點刪除，比較客戶點j的需求量和車輛剩余容量的大小，若客戶點j的需求量大于車輛剩余容量，則車輛返回配送中心開始新一輪路線尋找，否則重新選擇客戶點。

步驟6對螞蟻k構造解路徑用2-opt進行局部搜索優化，避免陷入局部最優。

步驟7根據公式τij( t+1)=(1 -ρ)τij(t)+Δτij更新信息素濃度，其中ρe∈( 0 ,1)。

步驟8若迭代次數小于iter_max，則轉步驟2；否則程序結束，輸出結果。

4 算例分析

假設坐標點1是某快遞公司在蘇州設立的一個大型分撥中心（本文只考慮配送作業），設其坐標為[12，6]。該快遞公司在蘇州市區內共有55個網點；配送車輛每天進行5個班次的運輸，配送開始時間分別為06：20、08：50、13：10、15：45和18：20，每個配送班次的作業時間為2.5 h；客戶坐標在邊長為40的矩形中隨機產生，需求為隨機從[100，300]取整，設為a0，如表1所示；同時表1中的需求數據也將用于計算雙十一期間情景S的服務時間，公式10+0.2×ps×(gsj-a0)，此部分數據不再單獨列出；非雙十一期間各客戶點服務時間為10 min；公司現階段擁有20輛1.5 T自有車輛，裝載容量為700件。

燃油成本（元）=單位體積的燃料成本×滿載耗油量×客戶點之間的距離。總旅行時間（min）=運輸時間+服務時間。

設93#汽油價格為7.65元/L[21]；滿載耗油量為0.06 L/km；自有車輛固定成本為500元/輛；外包車輛固定成本為1 000元/輛；車輛行駛速度為50 km/h；司機工資為40元/h與1.6元/km；單位裝卸成本為2元/件；若存在兩條或兩條以上運輸路徑總旅行時間小于時間窗2.5 h，則使用同一輛車進行分次運輸，并優先使用自有車輛。

本文假設該分撥中心在雙十一期間預測了三種可能存在的需求情景，發生的概率分別是0.3、0.3和0.4，螞蟻數量為80，信息素殘留系數為0.5，信息啟發因子為0.1，期望啟發式因子為0.5。各情景下客戶點的需求量如表2所示。另設定魯棒模型參數λ為1，?為100，算法迭代200次。

運用Matlab軟件分別對確定性模型和魯棒性模型求解。原確定需求成本為71 372元，總旅行時間為1 944 min，路徑圖見圖1。由于路徑1-19-16-1和1-30-28-25-1總旅行時間小于150 min，因此可以使用同一輛車進行分次運輸。同理，路徑1-9-6-27-1和1-23-22-1、1-31-35-1和1-36-37-33-1、1-49-55-1和1-5-3-1、1-21-17-1和1-50-54-1、1-24-20-42-1和1-13-7-1、1-39-40-1和1-2-4-1、1-46-44-1和1-32-26-1也分別使用一輛自有車輛進行運輸，其余路徑分別配置一輛自有車輛，共需要自有車輛15輛。其結果如表3所示。

魯棒優化模型的成本為92 433元，總旅行時間為2 935 min，路徑圖見圖2。其中路徑1-16-1和1-27-7-1、1-55-47-1和1-19-23-1、1-31-1和1-43-40-1、1-50-1和1-22-20-1、1-17-29-1和1-18-1、1-39-32-1和1-13-21-1、1-35-34-1和1-26-38-1、1-46-1和1-3-5-1、1-44-1和1-24-6-1分別使用一輛自有車輛進行運輸，其余路徑分別配置一輛自有車輛，因此共需要自有車輛23輛，外包車輛3輛。結果如表4所示。

表1 客戶點坐標及需求 件

表2 情景集下客戶點的運輸需求

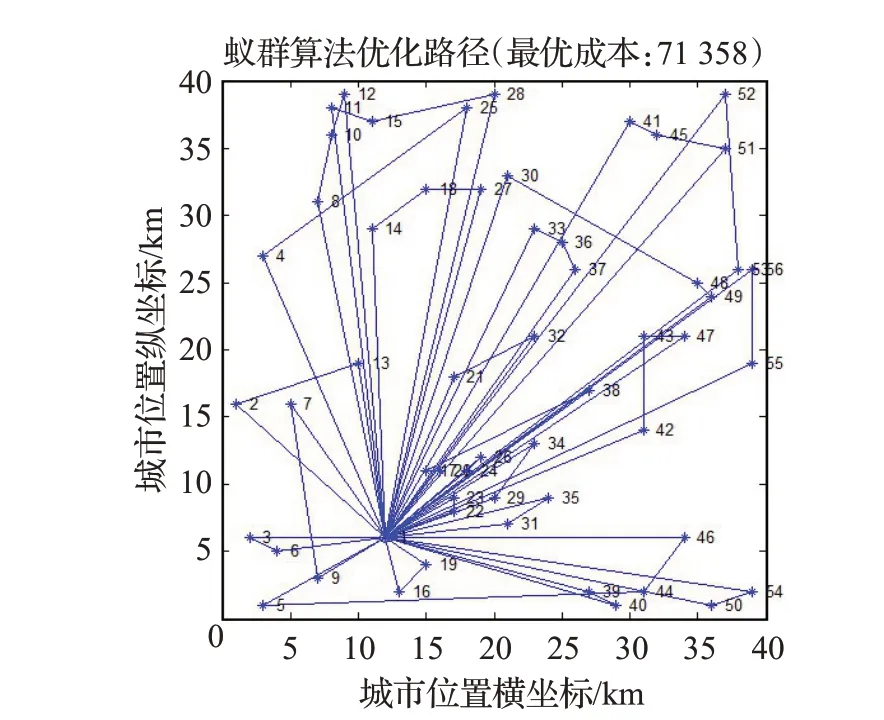
圖1 原確定需求車輛路徑

為了進一步比較魯棒模型的優勢，本文將三種情景集的運輸需求分別代入確定性模型計算相應的最優值并與魯棒優化模型進行比較，同時比較兩者在一輪運輸班次結束之后所花費的總旅行時間的差異，其結果如表5所示。對比發現：在成本方面，成本最優條件下魯棒模型的解與原需求的解差距最大，而與所有情景下的成本差距保持在10%左右。一方面是由于需求增加導致成本上漲；另一方面，由于魯棒模型是綜合考慮所有情景條件得到的，因此所有情景都可以接受，故差距穩定，證實了魯棒模型的抗干擾性和高成本的代價；而兩種情況各自對應的總成本之間差距較小，環比的最大值僅為1.90%。在旅行時間方面，一輪行車結束的總旅行時間存在較大差異，最多可節約47 min。由此可見，快遞企業可以在成本沒有大幅度變動的前提下優先考慮運輸時效，以減緩分撥中心壓力，保證快件及時送達配送站點。

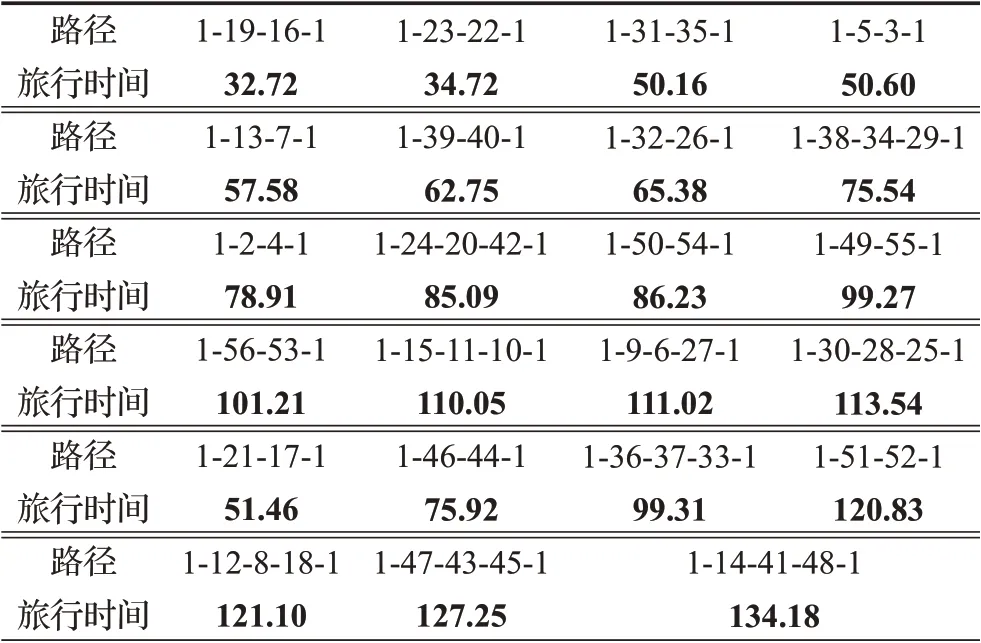
表3 確定性模型最優解 min

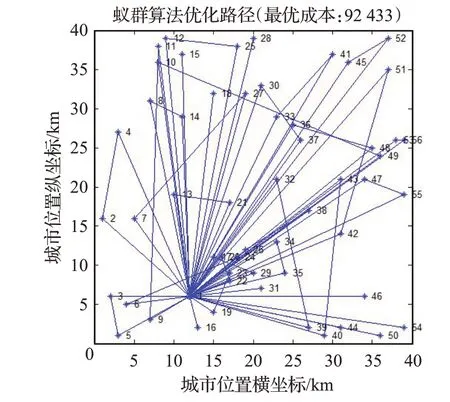
圖2 魯棒模型車輛路徑

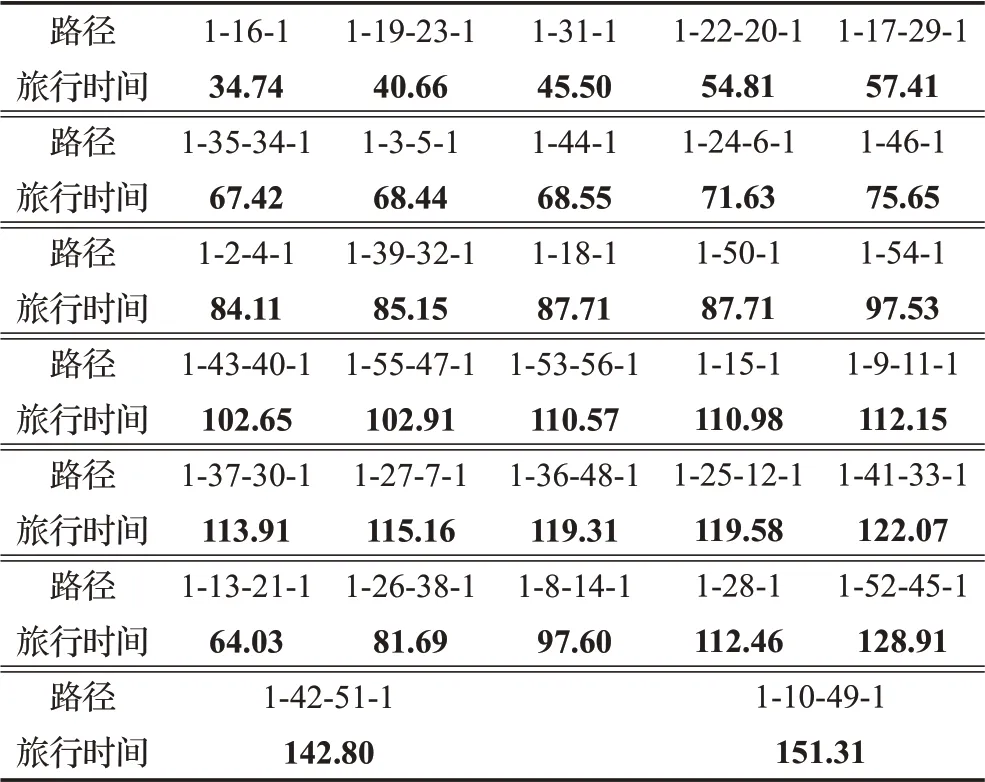
表4 魯棒優化模型最優解min

為找出公司規模與業務量和總成本之間的相關性，將需求在[200，700]范圍內，間隔50取整，算法運行結果見圖3。分析發現：隨著公司業務量的增加，且當超出公司自有車輛的規模時，運營成本增長較快；運輸費用的上升是導致企業利潤增長緩慢的原因之一。

為更加直觀地對比算法收斂性能，運用Matlab軟件，以原確定需求數據為背景，采用傳統蟻群算法和基于2-opt的蟻群算法對確定性模型進行求解，設置迭代次數為500次，結果見圖4。可以看出：相較于基本蟻群算法，改進后算法的探索性和收斂性強，求解的目標函數值更優。但由于本文算法添加了2-opt，故問題求解時間略有增加。

5 結論及未來工作

本文在確定性模型的基礎上，選用基于情景集下的魯棒優化方法優化分撥中心的配送網絡，為了避免蟻群算法在求解過程中陷入局部最優，采用2-opt進行局部搜索優化。并創新性地通過變化的快件數量，對客戶服務時間進行重新分配；通過對每條運輸路徑的時間計算，若存在兩條或兩條以上路徑的旅行時間之和滿足時間窗要求，則使用同一輛車進行配送，以實現對自有車輛的最大利用。提出的模型能夠在需求大幅浮動的情況下控制成本，同時保證每個運輸班次總旅行時間的合理性，提高了企業的運作效率。

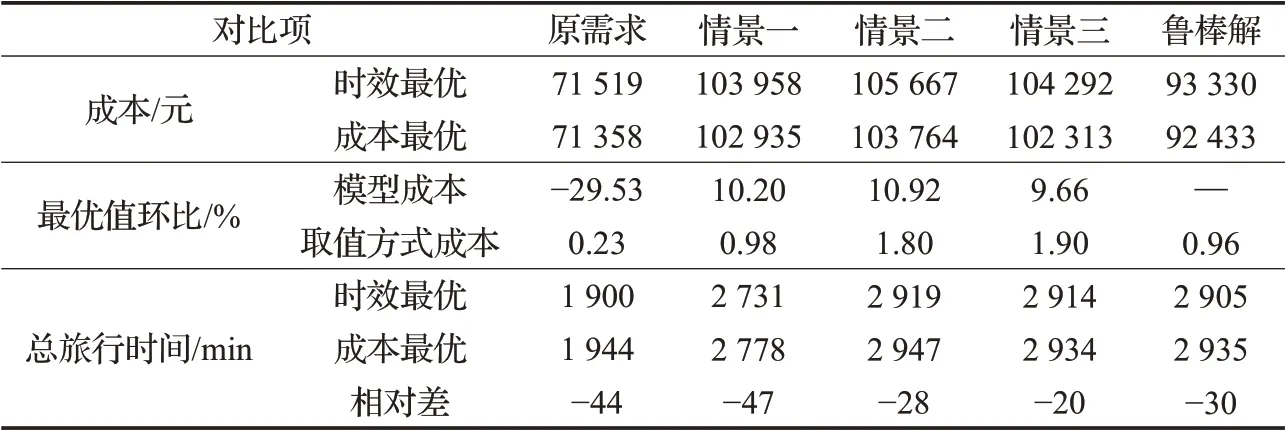
表5 確定性模型和魯棒模型的成本及總旅行時間差異對比

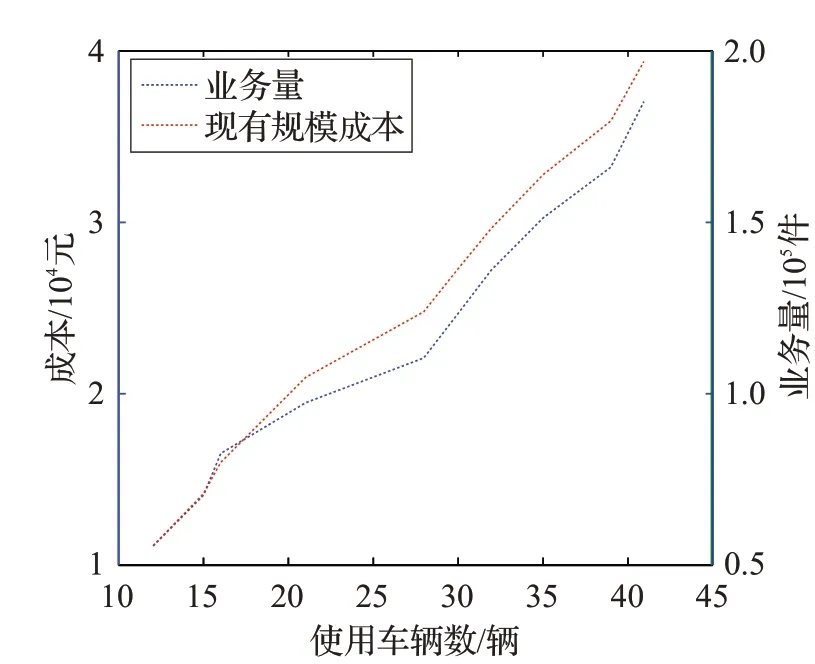
圖3 公司規模與業務量和運輸成本的相關性

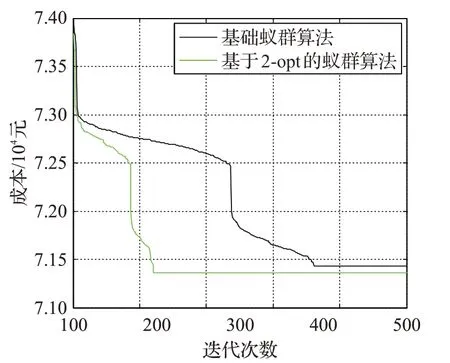
圖4 原確定需求下算法性能對比

在今后的工作中，會將客戶點的需求進行拆分，在充分利用自有車輛的前提下，提高車輛裝載率，以此實現設計路線的合理性，同時希望能夠發現更高效的算法改進策略。