基于卡爾曼濾波算法的上證50指數預測

梁　偉

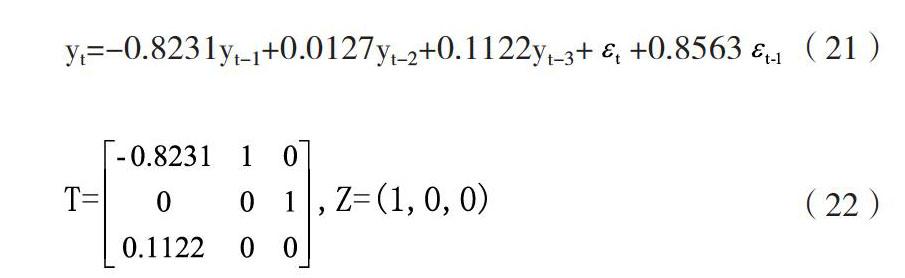
摘要： 本文基于ARMA模型構建卡爾曼濾波算法的線性狀態(tài)空間模型，然后利用ARMA模型的卡爾曼濾波算法來預測上證50指數，并且將預測結果與基于ARMA模型的預測結果進行了比較，結果表明，結合了ARMA模型的卡爾曼濾波算法的預測準確度為52.1%，明顯優(yōu)于單純的ARMA模型。

關鍵詞： ARMA模型 卡爾曼濾波算法 預測

一、引言

金融時間序列分析一直是學術界的研究熱點，同時各類數學模型及機器算法也在不斷地發(fā)展和優(yōu)化，ARMA模型及卡爾曼濾波算法都是非常有效的金融時間序列分析方法，本文將二者相結合使用以提高指數預測的準確度，具有一定的學術意義及現實可操作性。

在國外，卡爾曼（Kalman）和布塞（Bucy）在1960年發(fā)表了一篇名為《線性濾波和預測理論的新成果》的論文，提出了一種新的線性濾波和預測理論，被稱之為卡爾曼濾波。在國內，彭繼兵和唐春艷（2005）基于變維分形理論的卡爾曼濾波算法對股票價格進行了預測，結果發(fā)現基于變維分形理論的卡爾曼濾波動算法對股價的預測是有效的。劉向陽（2019）對幾種典型非線性濾波算法及其性能進行了分析，文章通過仿真實驗對四類濾波器性能進行了對比分析，研究結果表明，EKF 計算量小，PF 精度高，UKF和CKF具有較高的精度和較強的實時性。

二、卡爾曼濾波算法

（一）算法概念

卡爾曼濾波算法是一個最優(yōu)化自回歸數據處理算法，該算法由狀態(tài)方程和觀測方程組成的線性隨機系統(tǒng)的狀態(tài)空間模型來描述。該算法利用狀態(tài)方程的傳遞性，按線性無偏最小均方誤差估計準則，利用新觀測數據，對系統(tǒng)狀態(tài)變量作最佳估計。具體來講，狀態(tài)方程負責向前推算當前狀態(tài)變量和誤差協方差的估計值，為下一個時間狀態(tài)構造先驗估計。測量方程負責反饋，即將先驗估計和測量變量結合以構造后驗估計。卡爾曼濾波算法的這些特性非常適合用于金融時間序列短期預測，下面即為卡爾曼濾波算法進行金融時間序列短期預測對應的運行流程，如下：

系統(tǒng)狀態(tài)：X（k）=AX（k-1）+BU（K）+W（K）（1）

系統(tǒng)預測值：Z（k）=HX（k）+V（k）（2）

上面公式1、2即為卡爾曼濾波算法的線性狀態(tài)空間模型，其中X（k）是k時刻的系統(tǒng)狀態(tài)，U（K）是k時刻對系統(tǒng)的控制量，它可以為0。A和B是參數，對于多模型系統(tǒng)，它們是矩陣。Z（k）是k時刻的測量值。H是測量系統(tǒng)的參數，對于多測量系統(tǒng)，H為矩陣。W（k）和V（k）分別是系統(tǒng)狀態(tài)和測量值的噪聲。

假設現在的系統(tǒng)時刻是k，過程模型利用上一時刻的系統(tǒng)狀態(tài)預測現在的系統(tǒng)狀態(tài)：

X（k|k-1）=AX（K-1|K-1）+BU（k）（3）

在上式中，X（k|k-1）是k時刻的系統(tǒng)狀態(tài)預測結果，X（K-1|K-1）是（k-1）時刻系統(tǒng)狀態(tài)的最佳估計值。系統(tǒng)狀態(tài)已經更新，接下來更新X（k|k-1）對應的協方差，我們用P表示協方差，如下：

P（k|k-1）=AP（k-1|k-1）AT+Q（4）

在上式中，P（k|k-1）是X（k|k-1）對應的協方差，P（k-1|k-1）是X（k-1|k-1）對應的協方差，AT為A的轉置矩陣，Q是系統(tǒng)過程的協方差。

現在我們利用系統(tǒng)狀態(tài)的預測值及觀測值估計系統(tǒng)狀態(tài)的最優(yōu)值X（k|k），如下：

X（k|k）=X（k|k-1）+Kg（k）[Z（k）-HX（k|K-1）]

（5）

在上式中，Kg（k）為卡爾曼增益：Kg（k）=P（k|k-1）HT/[HP（K|K-1）HT+R]（6）

現在我們已經得到了k時刻系統(tǒng)狀態(tài)的最有估計值X（k|k），但是為了讓系統(tǒng)繼續(xù)運行下去，我們還需要更新k時刻系統(tǒng)狀態(tài)X（k|k）對應的協方差，如下：

P（k|k）=[1-Kg（k）H]P（k|k-1）（7）

以上便是進行短期價格預測的卡爾曼濾波算法的自回歸運算過程。

（二）算法應用

卡爾曼濾波算法是目前應用最為廣泛的濾波方法，在導航、控制及金融數據分析等領域都取得了較好的應用效果。卡爾曼濾波算法對系統(tǒng)狀態(tài)的估計可以是對當前系統(tǒng)狀態(tài)的估計（濾波），也可以是對于將來系統(tǒng)狀態(tài)的估計（預測），也可以是對過去系統(tǒng)狀態(tài)的估計（插值或平滑）。卡爾曼濾波算法對金融時間序列短期預測屬于對未來系統(tǒng)狀態(tài)的估計，通常通過MATLAB、Python及R語言來實現。以MATLAB為例，在利用卡爾曼濾波算法進行高頻交易的時候，投資者將高頻價格信息輸入卡爾曼濾波函數，就可以預測短期價格指數。

三、ARMA模型

（一）模型概念

自回歸移動平均模型（ARMA模型）由因變量對它的滯后值以及隨機誤差項的現值和滯后值回歸得到，該模型具體可分為移動平均（MA）模型、自回歸（AR）模型及自回歸移動平均模型。

1.MA（q）過程的表示形式：

（8）

在上式中，c為常數項，{}為白噪音過程。對于任意的t，MA（q）都是平穩(wěn)的。

2.AR（p）過程的表示形式：

（9）

在上式中，c為常數項，{}為白噪音過程。當特征方程的根全部落在單位圓之外時AR（p）過程是平穩(wěn)的。

3.ARMA過程的表現形式：

（10）

在上式中，{}為白噪音過程。ARMA過程的穩(wěn)定性取決于它的自回歸過程。

引入滯后算子L，上式可以寫成：（11）

其中，;。

（二）模型應用

1.ARMA模型的識別。利用自相關函數（ACF）及偏自相關系數（PACF）識別ARMA模型，具體步驟為：第一步，通過ADF檢驗判斷時間序列的平穩(wěn)性;第二步，利用ACF、PACF及它們的圖形來確定ARMA（p，q）模型的參數p、q。

2.ARMA模型的診斷與檢驗。具體步驟為：第一步，通過t檢驗檢驗模型參數的顯著性;第二步，通過Q統(tǒng)計量檢驗殘差序列的隨機性。

四、基于ARMA模型的線性狀態(tài)空間模型的建立

基于ARMA模型建立卡爾曼濾波算法的線性狀態(tài)空間模型，即將ARMA模型轉化為狀態(tài)空間模型，本文利用Harvey方法進行模型轉化。

考慮上面均值為0的ARMA（p，q）過程yt：

令m=max（p，q+1）且將上式改寫為：（12）

在上式中，，，并且（因為m>q）。

現在我們將上面提到的卡爾曼濾波算法所對應的狀態(tài)空間模型（公式1、2）轉變?yōu)閺V義高斯線性狀態(tài)空間模型，如下：

狀態(tài)方程：（13）

觀測方程：（14）

在上式中，是m維狀態(tài)向量，是k維觀測向量，dt和ct分別是m維和k維的確定性變量，Tt和Zt分別是m×m和k×m的系數矩陣，Rt是m×n矩陣，且{}和{et}分別是n維和k維高斯白噪聲序列。

Harvey給出了具有m維狀態(tài)向量st的狀態(tài)空間的一種形式，該狀態(tài)向量的第一個元素是yt，即s1t=yt，st的其它元素通過遞歸得到，由ARMA（m，m-1）模型可以求出：

（15）

其中，且如前述定義，考慮可以得到：（16）

重復上述過程，可得：（17）

進一步可得：（18）

將上述方程綜合起來，可以得到如下狀態(tài)空間模型：

（19）

（20）

以上即為基于ARMA模型建立卡爾曼濾波算法對應狀態(tài)空間模型的具體過程。

五、上證50指數預測

（一）數據選取

選取上證50指數日收盤價數據，時間區(qū)間為2018年1月2日到2019年8月30日，一共406個數據，然后計算日收盤價的對數收益率序列（日收益率），計算公式為：yt=ln（Pt/Pt-1），公式中Pt表示上證50指數第t日收盤價，Pt-1表示第t-1日收盤價，一共得到405個對數收益率數據。

（二）基于結合了ARMA模型的卡爾曼濾波算法的指數預測

本文通過Python3.0平臺進行基于卡爾曼濾波算法的上證50指數預測，首先獲取指數日收盤價、對數收益率（日收益率序列），然后建立收益率序列的ARMA模型。aic-order與hqic-order均給出AR過程階數為3，MA過程階數為1，符合前面假設：p >= q+1，故令order = （3，1）。通過ljung-box檢驗，判斷ARMA（3，1）模型殘差序列是否存在滯后相關，檢驗結果表明滯后40階以內的p-value均大于0.05，故可以判斷殘差中沒有顯著的序列相關性，接下來進行模型的轉化。

通過Harvey方法實現ARMA模型向拉爾曼濾波算法狀態(tài)空間模型的轉化部，可得：

yt=-0.8231yt-1+0.0127yt-2+0.1122yt-3++0.8563（21）

（22）

接下來運行基于ARMA模型的卡爾曼濾波算法，上證50指數預測結果與真實值如下圖：

圖1 上證50指數卡爾曼濾波算法短期預測圖

進一步計算卡爾曼濾波算法預測的準確度為0.5210。

（三）基于ARMA模型的指數預測

單純基于ARMA模型的上證50指數預測結果如下圖：

圖2 上證50指數ARMA模型預測圖

基于ARMA模型的上證50指數預測準確度為0.4687。

六、結論

由上面預測結果可知，相比于ARMA模型的預測結果，結合了ARMA模型的卡爾曼濾波算法在上證50指數的預測中，其預測的準確度高于單純的ARMA模型，準確度提高了5.2%。說明卡爾曼濾波算法經過與ARMA模型的結合，對于噪聲過濾效果更好。不過，結合了ARMA模型的卡爾曼濾波算法相對其它機器算法及數學模型，預測的準確度還不夠高，仍然存在較大的優(yōu)化空間。

參考文獻：

[1]Kalman R E，Bucy R S.New Results in Linear and Prediction Theory.Trans ASME，J? Basic Eng，1961;83：95-107.

[2]彭繼兵，唐春艷.基于變維分形理論的卡爾曼濾波實時跟蹤預測模型在股票價格預測中的應用[J].機算機工程與應用，2005（13）：218-223.

[3] 劉向陽.幾種典型非線性濾波算法及性能分析[J].艦船電子工程，2019（7）：32-35.

作者系山西財經大學金融學院金融專業(yè)2018級碩士研究生