具有對數(shù)型衰減初值的半線性波動方程解的爆破

蔡春玲, 黃守軍

(安徽師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,安徽蕪湖 241002)

1 引言

本文主要研究如下低維空間中半線性波動方程的柯西問題

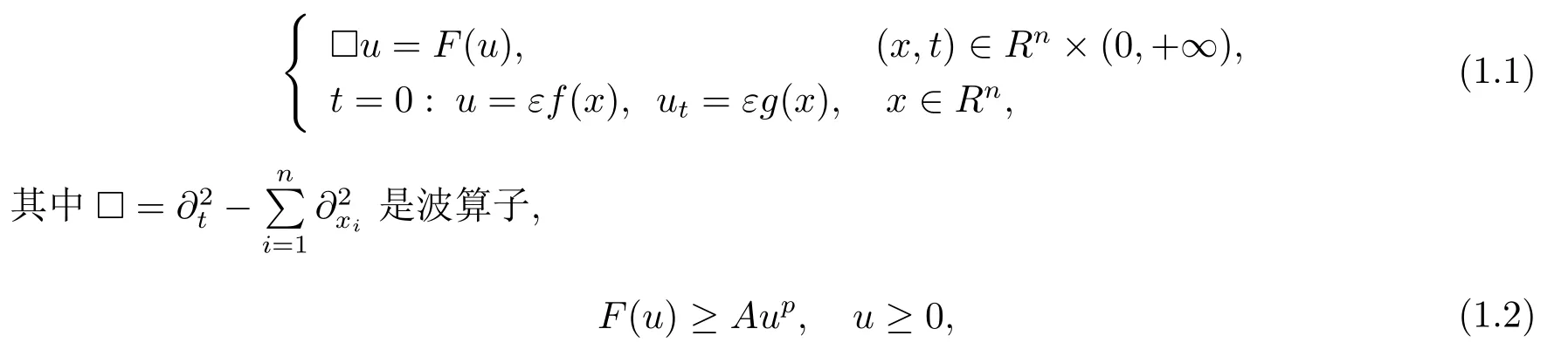
A>0,p>1,ε>0 是小參數(shù).考慮n=2 和n=3 情形, 且p>p0(n), 其中p0(n) 是下列二次方程的正根

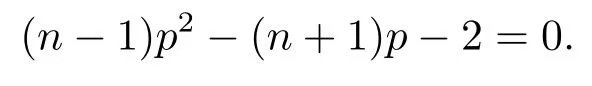
對于半線性波動方程柯西問題(1.1), 已經(jīng)有了很多關(guān)于解整體存在和爆破的相關(guān)結(jié)果.當初值f(x),g(x) 具有緊支集且F(u) =|u|p時, 柯西問題(1.1) 有Strauss 猜想.即: 初值“充分小”,p>p0(n), 則式(1.1) 有整體解; 初值在某種意義下為正, 且1

對于n=3 情形, John[1,2]得到如下結(jié)果: 設(shè)F(u) 滿足

對于臨界情形p=p0(3) 和p=p0(2), Schaeffer[5]已經(jīng)證明了即使對于小初值, 式(1.1)不存在整體解.

至此, 對于n=2 和n=3 的情形, Strauss 猜想已經(jīng)得到完整驗證.

對于高維情形n ≥4, 次臨界情形1p0(n) 被Georgive, Lindblad 和 Sogge[7]證明.而臨界情形p=p0(n) (n ≥4) 被Yordanov 和Zhang[8]以及Zhou[9]分別獨立驗證, 并且對于情形n ≥2, Zhou 和Han[10]給出了臨界情形p=p0(n) 解的生命跨度的上界估計, 有關(guān)最新結(jié)果也可參見Rammaha,Takamura, Uesaka 和Wakasa[11].

若初值不具有緊支集, 則式(1.1) 解的情況會發(fā)生變化.事實上, 對于n= 3 情形,Asakura[12]設(shè)F(u) 滿足式(1.3), 且p>p0(3), 初值f(x)∈C3(R3),g(x)∈C2(R3).如果初值滿足

最近, Kong 和Liu[15]提出雙曲Yamabe 問題, 考慮(1+n) 維 Minkowski 空間中的Yamabe 方程解的整體存在與爆破.Minkowski 時空中的雙曲Yamabe 問題為如下半線性波動方程柯西問題所刻畫

在文 [15]中, Kong 和 Liu 證明: 若初值f(x)∈C3(Rn),g(x)∈C2(Rn)(n=2 或 3), 且滿足

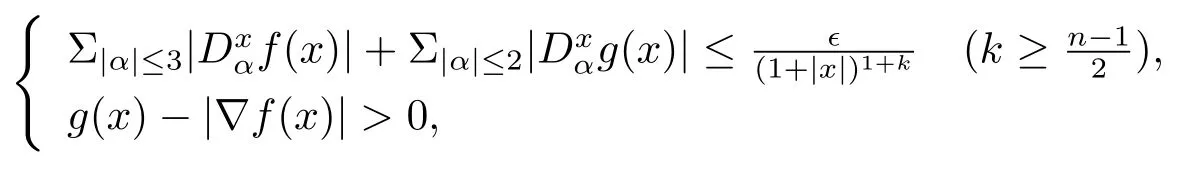
則柯西問題(1.6) 的光滑解整體存在; 若初值f(x)∈C3(Rn),g(x)∈C2(Rn) (n=2 或3), 且滿足

本文研究一類具有衰減初值的半線性波動方程的柯西問題(1.1).不同于Asakura[12]和Kong 和Liu[15], 假設(shè)初值是具有形如式(2.1) 的對數(shù)型的衰減, 比代數(shù)衰減更緩慢一些.得到了半線性方程的柯西問題(1.1) 的解在有限的時間內(nèi)爆破, 并得到了生命區(qū)間的下界.

2 主要結(jié)果

下面給出本文主要結(jié)果.

定理2.1設(shè)f(x)∈C3(Rn),g(x)∈C2(Rn)(n=2 或3).若初值滿足如下條件

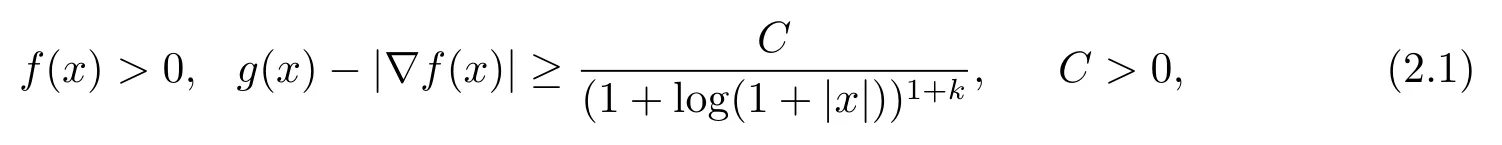
這里C0是與ε無關(guān)的正常數(shù).

定理2.1 中解的正性可由引理3.3 保證.由定理2.1, 可得Yamabe 問題(1.6) 的結(jié)論.

推論 2.1對于n=2 和n=3 情形的 Yamabe 問題 (1.6).設(shè)f(x)∈C3(Rn),g(x)∈C2(Rn) 且滿足式(2.1),則柯西問題(1.6)的解存在區(qū)間為[0,T?), 生命跨度T?的下界由式(2.2) 給出.

注2.1Kong 和Liu[15]未明確給出Yamabe 問題(1.6) 解的生命跨度的估計.

注2.2對于F(u) 滿足式(1.3), 初值滿足式(1.5), 且Tsutaya[13]指出柯西問題(1.1) 的解必發(fā)生爆破, 并給出同樣的下界估計式(2.2).由此, 初值的對數(shù)型衰減雖比代數(shù)型衰減慢, 但不影響生命跨度的下界估計.

注 2.3在文獻[13]中, Tsutaya 設(shè)F(u) =A|u|p,A> 0.若初值滿足f(x) = 0,則生命跨度T?滿足其中c0為與C無關(guān)的正常數(shù).因此, 猜測柯西問題(1.1) 的生命跨度T?也滿足其中c1為與ε無關(guān)的正常數(shù).

3 主要結(jié)果的證明

在這一節(jié)中, 將給出一些引理以及定理2.1 的證明.盡管所需引理在Kong 和Liu[15]和Kubota[16]中已經(jīng)給出, 但是為了完整起見, 在此依然將其列出, 證明可參見Kong 和Liu[15]和Kubota[16].

引理3.1考慮下列柯西問題

其中n=2 或3.當f(x)∈C3(Rn),g(x)∈C2(Rn),w(t,x)∈C2(Rn), 有

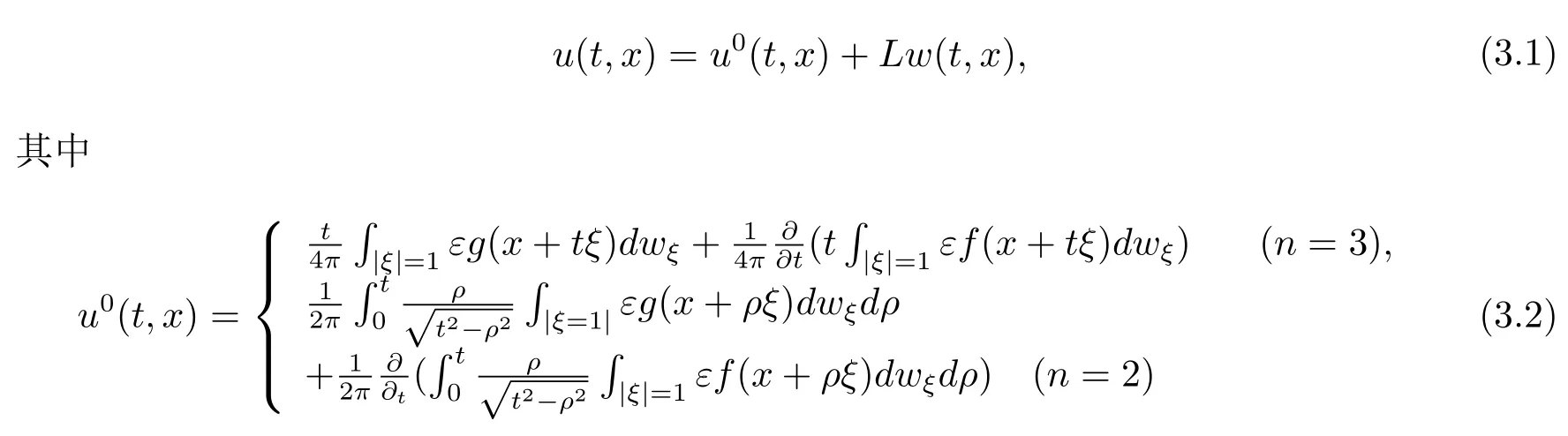
是柯西問題

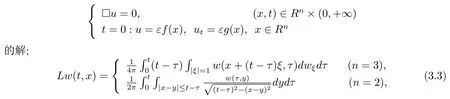
是柯西問題

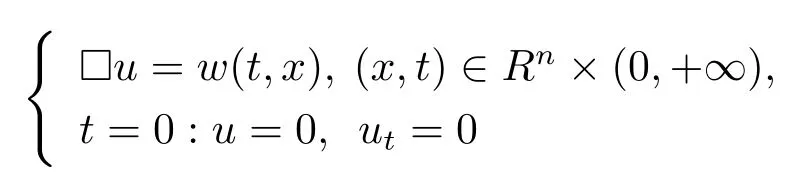
的解.

引理 3.2若b(λ) 是 (?∞,∞) 上連續(xù)函數(shù), 則

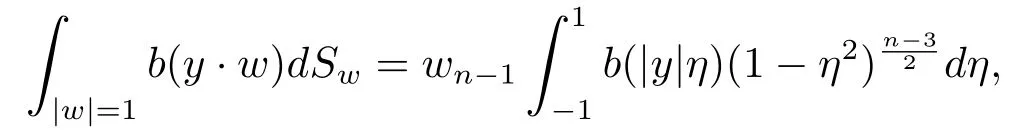
引理3.3若f(x)∈C3(Rn),g(x)∈C2(Rn) 滿足式(2.1), 則當ε充分小時, 柯西問題(1.1) 在[0,+∞) 上有正的C2解.

證明參見Kong 和Liu[15], 此處從略.

定理2.1 的證明利用John[1]和Kong 和Liu[15]中的迭代法來證明.由引理3.3 知, 只要u存在, 則u>0.當n=3 時, 由式 (3.2) 和 (2.1) 有

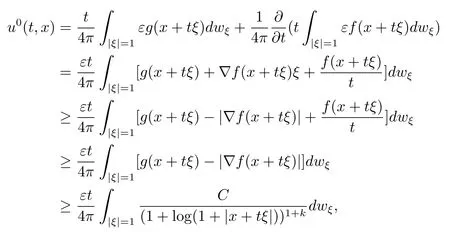
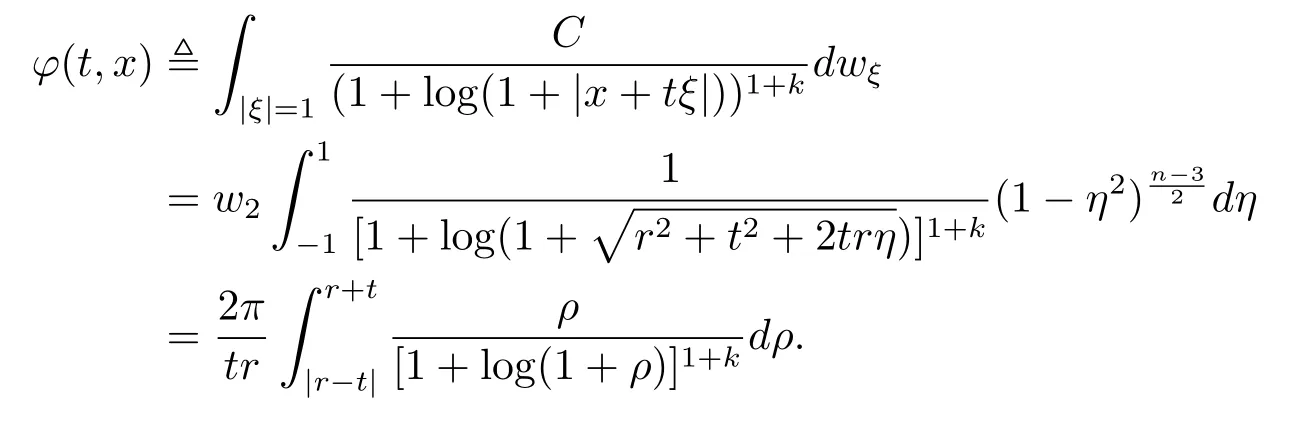
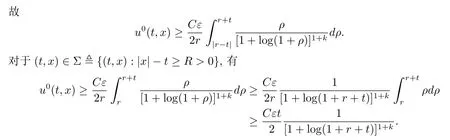
若函數(shù)p(t,x) 是 Cm(m ≥2) 光滑的, 記為p(t,x) 在半徑為r的球面上的平均值, 即由式 (3.3) 得

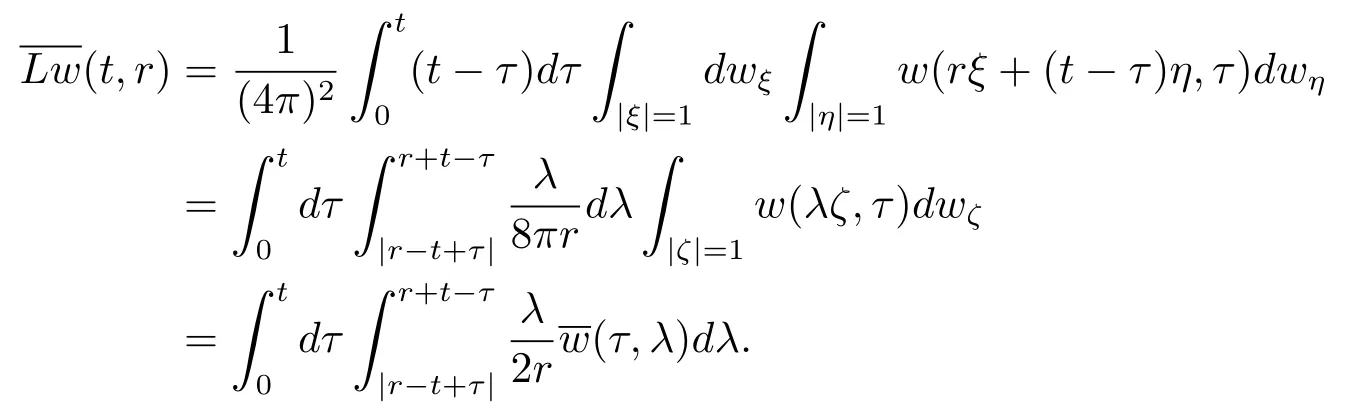
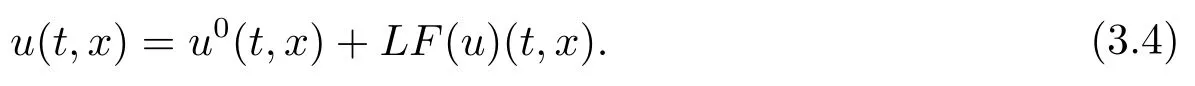
又由u>0, 成立

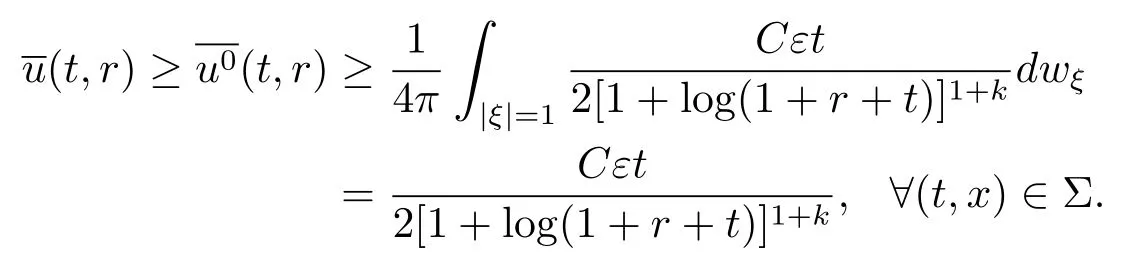
其中a,b,c均為正常數(shù).顯然當式 (3.6) 是滿足的.由式 (3.5)–(3.6),

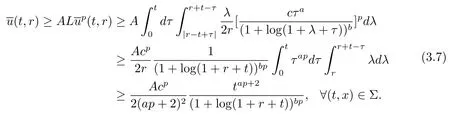
一直迭代下去, 并比較式(3.6) 和(3.7), 可定義如下序列{aj},{bj},{cj},

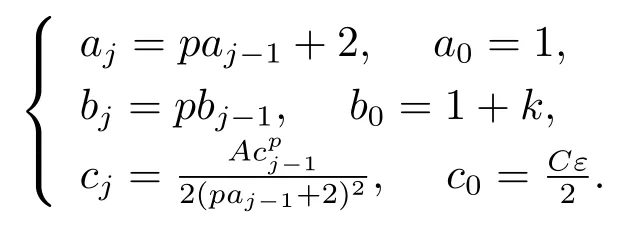
從而有

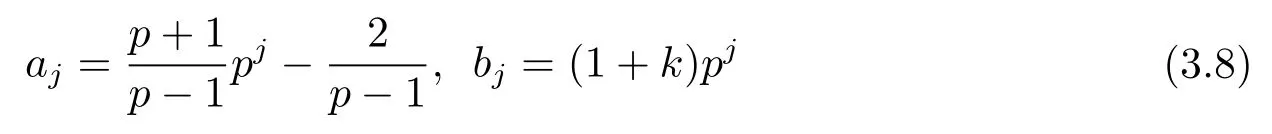
和

因此可以得到

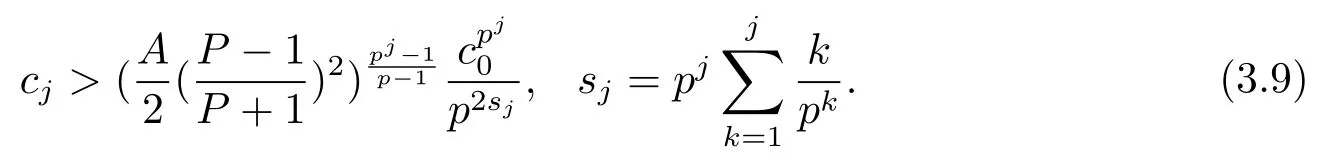
聯(lián)立式(3.6), (3.8) 和(3.9) 得到其中

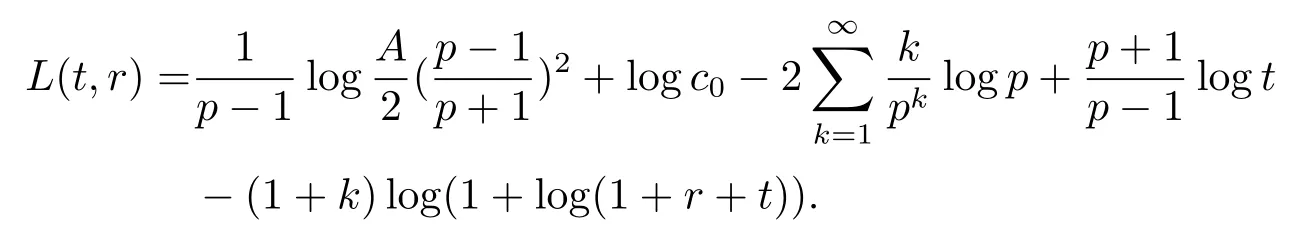
固定p, 從而有

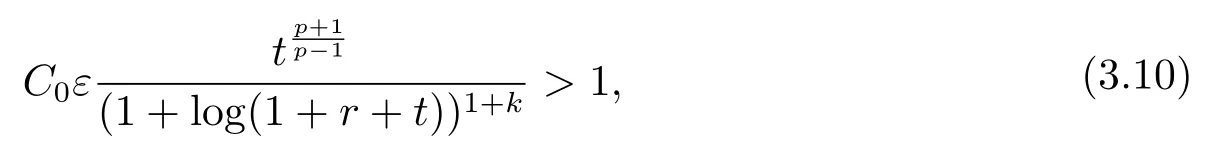
當n=2 時, 由式 (2.1) 和 (3.2) 有

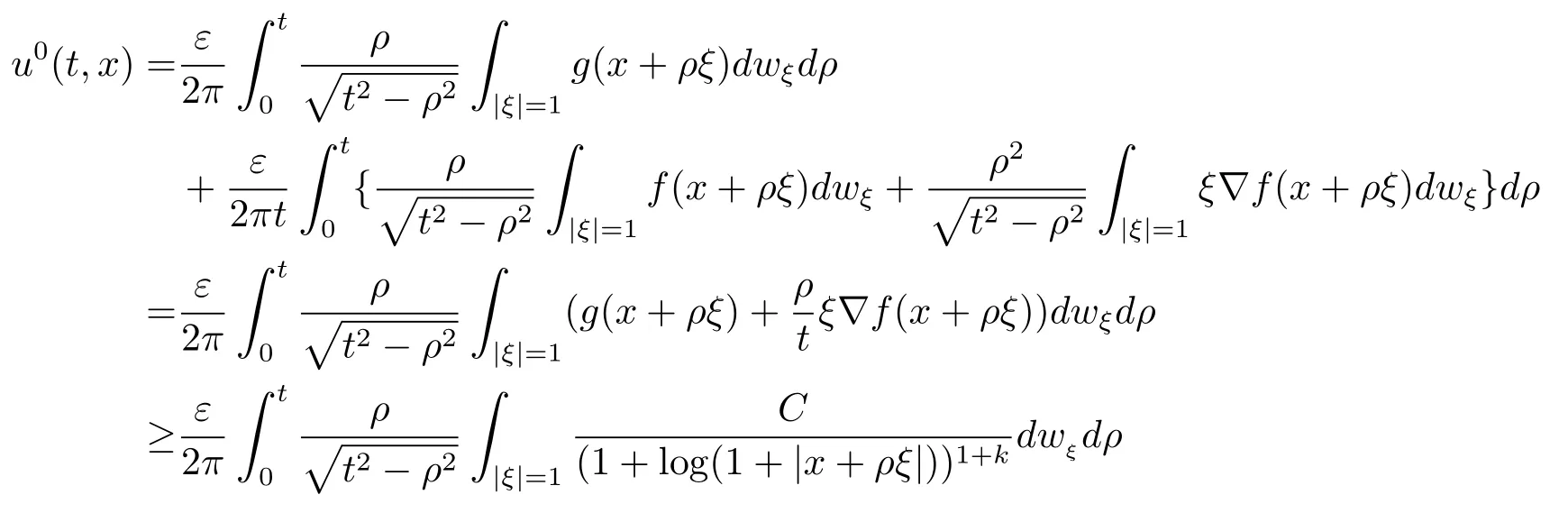
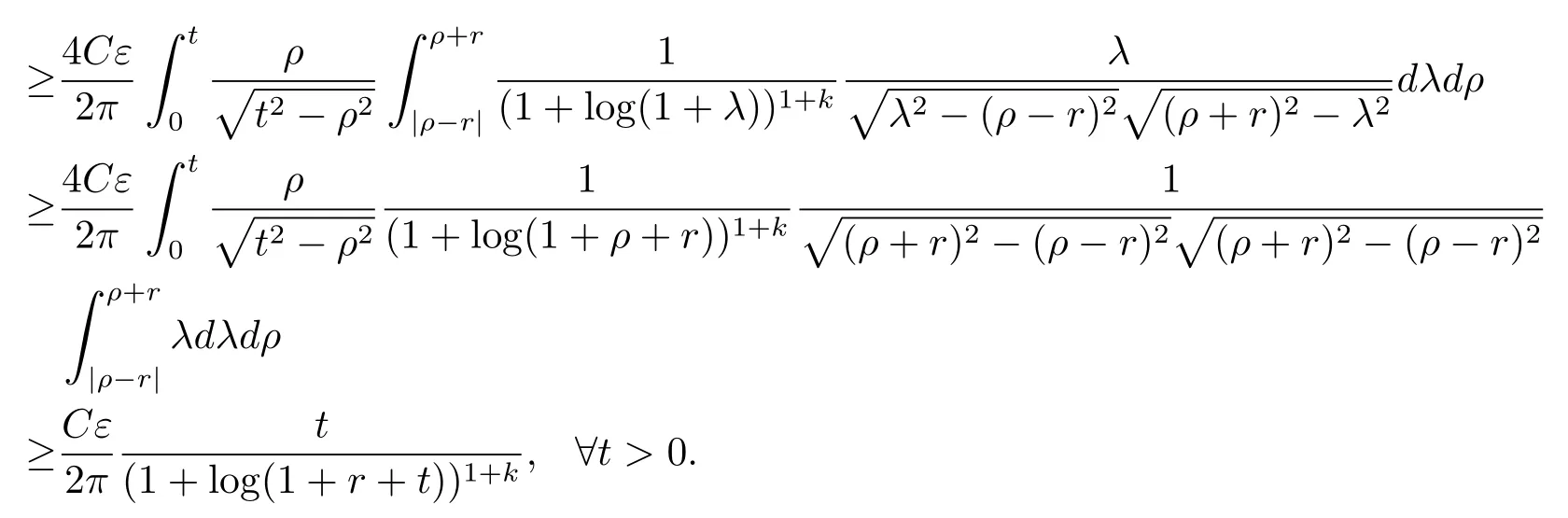
類似地, 設(shè)u有下列形式的估計

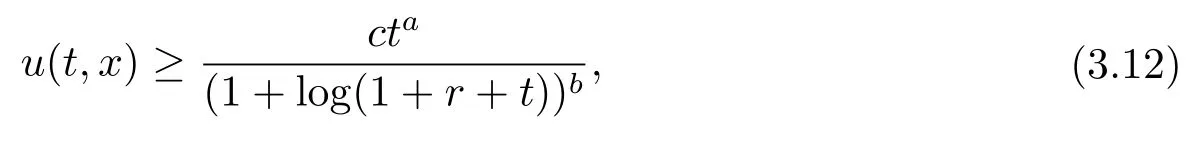
其中a,b,c均為正常數(shù).顯然當時, 式 (3.12) 是滿足的.由式 (3.4)和(3.12), 可知

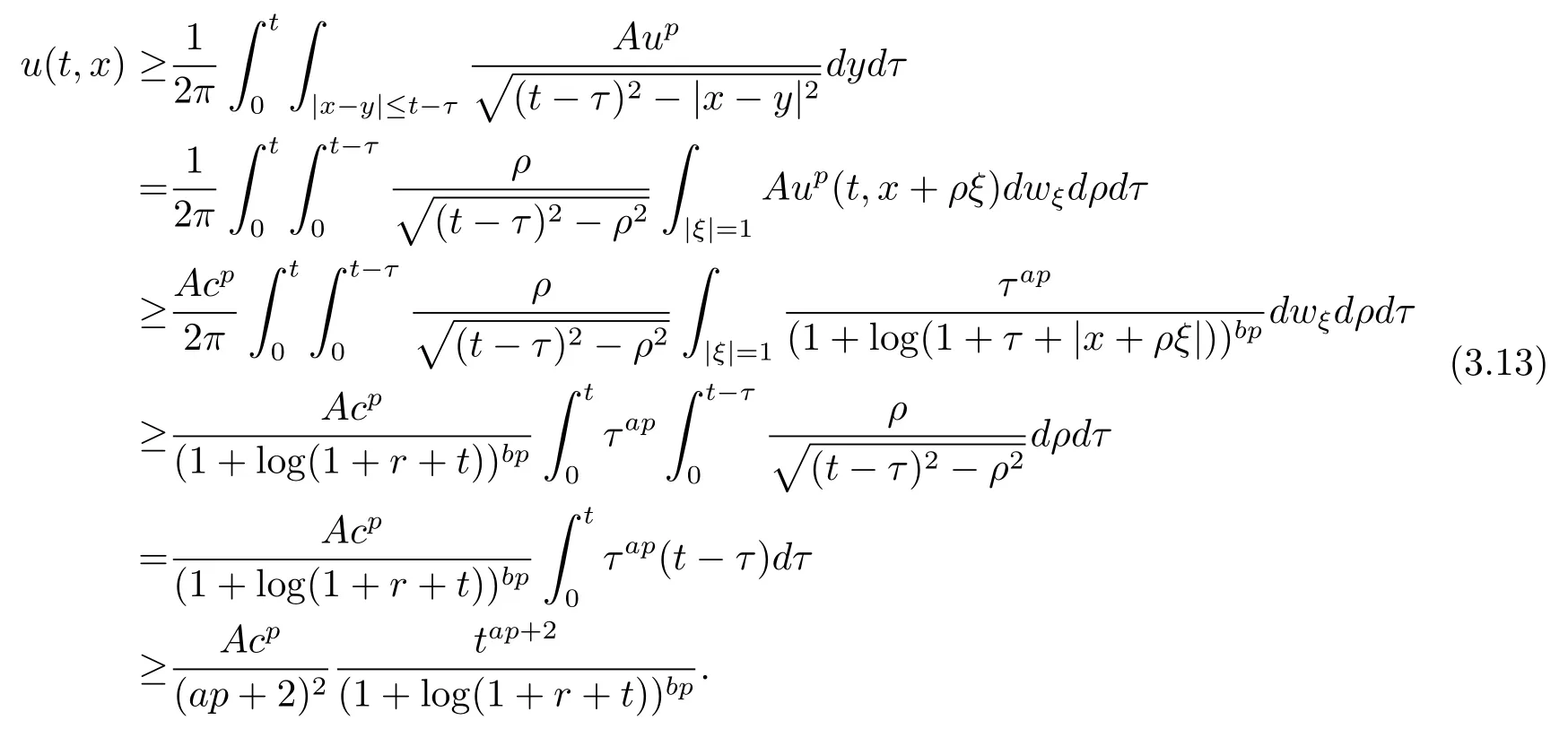
一直迭代下去, 并比較式(3.12) 和(3.13), 可定義如下序列{aj},{bj},{cj},

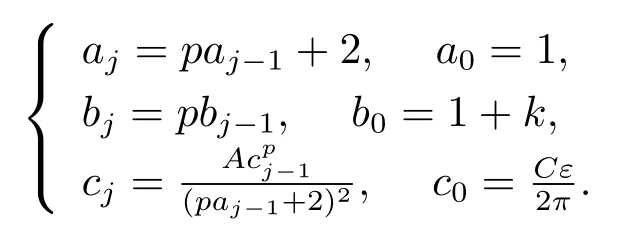
從而可求得

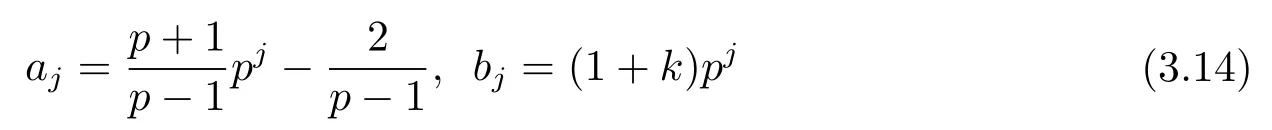
和

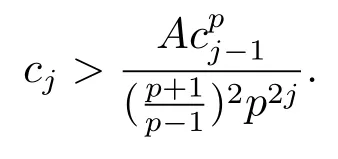
因此可以得到

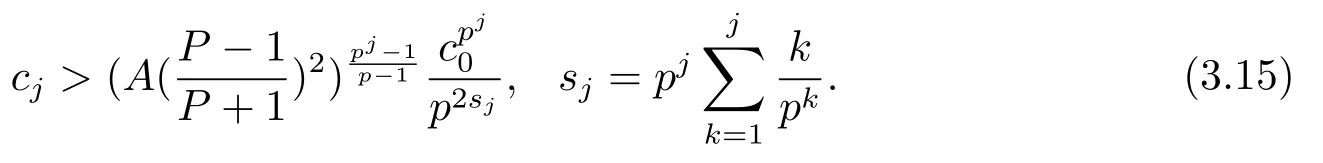
聯(lián)立式(3.12), (3.14) 和(3.15), 可得

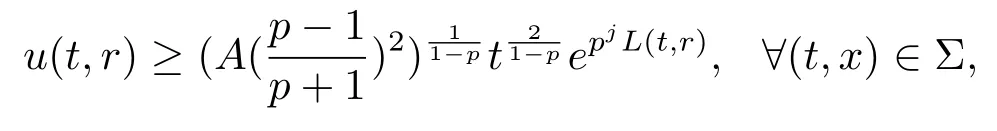
其中

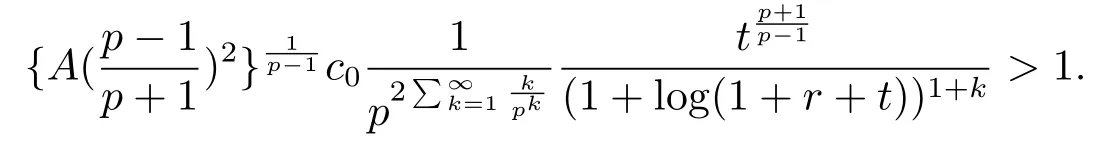
固定p, 從而有

從而由式(3.16) 可得n=2 情形下生命區(qū)間的下界估計

因此柯西問題(1.1) 的解不會整體存在, 解的生命跨度由式(3.11) 和(3.17) 給出.證畢.