基于分數階的自抗擾最優導引律

顧凱

摘 要：針對機動目標攔截問題，本文提出了一種基于分數階微積分的自抗擾最優導引律。首先，介紹了分數階微積分理論和自抗擾技術。然后分析彈目相對運動關系，通過分數階變階次建模和最優控制理論推導出分數階導引律。由于在目標的攔截過程中，目標的機動信息難以獲取，本文將目標的加速度當作未知擾動，通過擴張觀測器對其進行估計補償。最后仿真結果表明：與傳統比例導引法相比，本文設計的導引律能夠保持比例導引法良好的追蹤性能且攔截時間更短，過載變化平穩，解決了傳統比例導引法下，由于缺少目標的機動信息而導致末端過載突變的問題。

關鍵詞：機動目標;自抗擾;分數階微積分;最優控制

中圖分類號：TJ765.3文獻標識碼：A

在機動目標攔截過程中，由于目標的運動信息難以獲取，導致在采用傳統比例導引法時，彈道末段的需用過載會急劇增大[1]。為了改善這種情況，文獻[2]提出了滑模變結構制導律，該制導律對參數攝動和外界干擾不敏感，目標機動對其影響不大，但存在抖振的問題，影響制導性能。文獻[3]結合最優制導方法和變結構制導方法的復合制導律，但該方法過于復雜，難以進行工程應用。文獻[4]提出了一種H∞制導律，該制導律無需目標加速度信息，但Hamilton-Jacobi微分不等式的求解比較困難。本文設計的基于分數階的自抗擾最優導引律，能夠有效的抑制視線速率的發散，從而使過載變化更加平穩。把設計結果和比例導引法進行比較發現，該方法需用過載小，制導精度高，算法形式簡單，易于實現，具有很高的工程實用價值。

4 仿真驗證

為了驗證所設計的分數階微積分的自抗擾最優導引律的正確性和有效性。本文在Matalab環境進行仿真驗證，并與傳統比例導引法進行比較。

仿真結果如下所示：

由圖2可以看出，基于分數階的自抗擾最優導引法能夠準確的命中目標，同時所需時間更短。由此可見，分數階自抗擾最優導引律能夠保持傳統比例導引法良好的跟蹤性能，且能更快的命中目標。

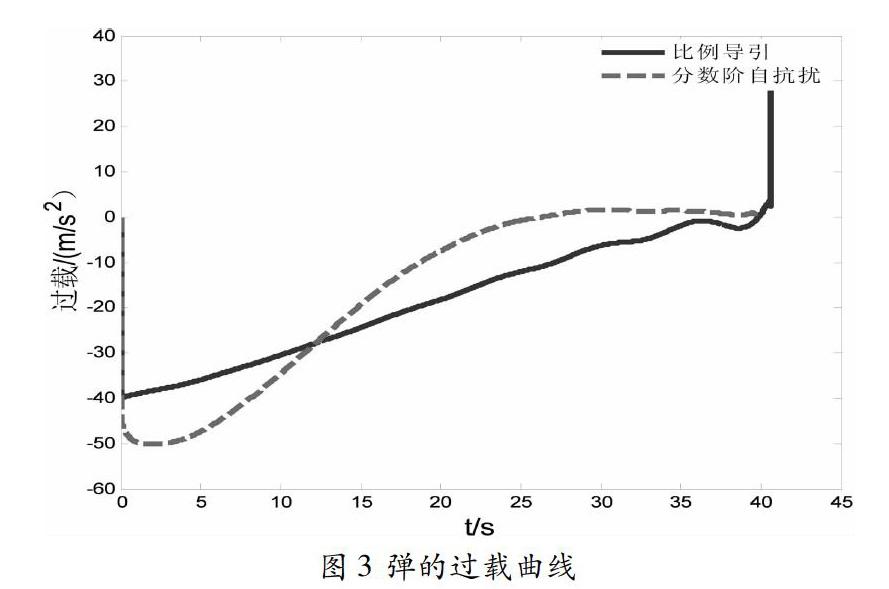
由圖3可以看出，相比于比例導引法，分數階自抗擾最優導引法的過載分布更為合理。在導彈命中末端，比例導引法的過載值會突然增大，這在實際情況下往往無法達到，從而會導致脫靶。而分數階自抗擾最優導引法能夠很好的解決這一缺陷，彈的過載在飛行的后半段幾乎趨近于0附近，且在末端沒有突變。

5 結論

本文將分數階微積分理論與最優控制理論相結合，通過自抗擾技術對目標加速度進行估計補償從而設計了一種新的分數階自抗擾最優導引律，該制導律繼承了比例導引法良好的跟蹤性能，同時解決了比例導引法在打擊動目標時，末端過載會突然增大的問題。仿真結果表明，相比于比例導引法，分數階自抗擾最優導引律命中時間短，過載分布更為合理，且末端過載無突變。

參考文獻：

[1]司學慧，李小兵.一種攔截機動目標的最優制導律設計[J].現代防御技術，2011，39（4）.

[2]陳昌旭，李洋，祁琪，孫勝.基于滑模變結構的導彈制導律設計[J].兵器裝備工程學報，2016（12）：61-64.

[3]HU Z，TANG X，WANG Y.A 3-Dimensional Robust Guidance Law with Impact Angle Constraint[C].Chinese Control and Decision Conference，IEEE，2011：999-1006.

[4]Shieh C S.Tunable H∞ robust guidance law for homing missiles[J].2004，151（1）：103-107.

[5]Ricardo Almeida，Dina Tavares，Delfim F.M.Torres.Fractional Calculus[M].The Variable-Order Fractional Calculus of Variations.2019.

[6]朱斌.自抗擾控制入門[M].北京：北京航空航天大學出版社，2017.

[7]薛文超.自抗擾控制的理論研究[D].中國科學院研究生院，2012.