充液撓性航天器姿態機動控制的多目標優化

朱 銳，郭 毓，王 璐，鐘晨星

（1.南京理工大學 自動化學院，江蘇 南京 210094；2.華為技術有限公司 南京研究所，江蘇 南京 210012；3.中國電子科技集團公司第二十九研究所，四川成都 610036）

0 引言

隨著空間技術的發展與航天需求的不斷增長，現代航天器的飛行任務呈現出多樣化趨勢，要求航天器既具有長的在軌工作壽命，又能夠完成復雜任務［1-2］。這使現代航天器的結構、尺寸日趨復雜與龐大，并且需要攜帶大量的液體燃料［3-4］，因為液體燃料不但能夠滿足能量性能要求，而且經濟性好、實用性強、燃燒時間長，適用于航天器飛行。此外，為降低發射成本，現代航天器廣泛采用輕質附件，如太陽能帆板、大型柔性天線等，這使航天器的撓性越來越大。因此，大型充液撓性航天器已成為未來航天器發展的重要方向之一。

現代航天任務對航天器姿態控制的要求越來越高。例如對地觀測衛星，為達到在軌高分辨率跟蹤監測的目的，既要求其姿態具有大角度快速機動、快速穩定的能力，又要求具有甚高穩態指向精度與穩定度［5-6］。然而，已有研究發現，充液撓性航天器因攜帶大量液體燃料和大型輕質撓性附件，其姿態控制系統具有剛-柔-液耦合的復雜非線性動力學特性，姿態機動極易誘發液體晃動和撓性附件振動，這對實現航天器姿態大角度快速機動、快速穩定控制提出了巨大挑戰。已有研究發現，路徑規劃是提高航天器姿態機動性能的關鍵因素之一，受到了國內外學者的廣泛關注。文獻［7］在探測器執行空間任務時采用Bang-Coast-Bang（BCB）型路徑進行快速機動，但是該路徑仍存在因角加速度突變易引起撓性附件振動的問題。文獻［8-9］分別提出了S 函數型角速度的機動路徑和三段式拋物線型角加速度的機動路徑，減少了姿態機動對撓性附件振動的激發。文獻［10］提出了一種三段式正弦型角加速度的機動路徑，使機動路徑更為平滑，進一步提高了姿態機動的快速性和穩態指向精度。文獻［11］提出了一種七段式正弦型角加加速度曲線的路徑，同時結合模糊多目標粒子群優化算法，對機動路徑參數進行優化，可以兼顧多項性能指標，實現撓性航天器快速機動、快速穩定。然而，現有文獻大多研究的是剛體或撓性航天器的姿態機動控制問題，研究充液撓性航天器姿態機動路徑的文獻還很少。

本文針對充液撓性航天器姿態快速機動、快速穩定的控制要求，設計了一種基于正弦型加加速度的七段式姿態機動路徑規劃方案，結合云多目標粒子群優化算法，聯合優化充液撓性航天器的控制器參數和機動路徑參數，以減小液體晃動和撓性附件振動對航天器姿態機動控制的影響，提高充液撓性航天器姿態機動的快速性和機動完成后的穩定度。

1 充液撓性航天器動力學模型及姿態控制系統結構

1.1 充液撓性航天器動力學模型

在混合坐標系下，一類帶有撓性太陽能帆板及液體燃料的三軸航天器的姿態動力學方程、撓性附件振動方程和液體燃料晃動方程可分別描述為［11］

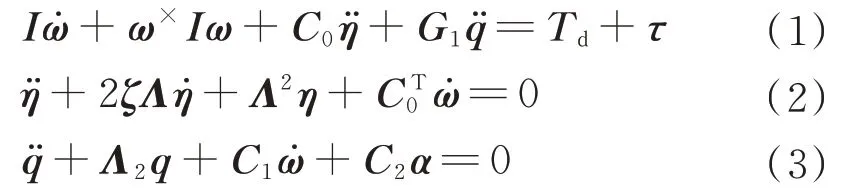
式中：I∈R3×3為航天器轉動慣量；ω∈R3×1為航天器本體坐標系相對慣性坐標系的角速度；ω×∈R3×3表示ω的斜對稱矩陣；C0∈R3×n為撓性振動與星體姿態運動的耦合系數矩陣；G1∈R3×m、C1∈Rm×3、C2∈Rm×3為液體晃動與星體姿態運動的耦合系數矩陣；τ∈R3×1為控制力矩矢量；Td∈R3×1為環境干擾力矩；ζ∈Rn×n為撓性體 振動模態阻尼比；Λ∈R3×1為撓性體振動模態頻率矩陣；Λ2∈Rm×m為液體晃動模態頻率平方矩陣；η∈Rn×1為撓性體振動模態矢量；q∈Rm×1為液體晃動模態矢量；α∈R3×1為航天器的姿態角矢量。

1.2 姿態機動路徑規劃

由于充液撓性航天器具有剛柔液動力學耦合的特點，在進行大角度姿態機動過程中，常常會導致液體的劇烈晃動和撓性帆板的強烈振動，降低了姿態機動的快速性和穩定性。為保證航天器姿態快速機動的同時減少姿態機動對撓性附件振動和液體晃動的激發，需對姿態機動路徑進行規劃。當前應用較為廣泛的是BCB 型路徑，采用該路徑一定程度上可以改善姿態機動的性能，但由于殘余振動較大，機動完成后的指向精度和穩定度難以提高。為提高充液撓性航天器姿態機動控制的性能，本文采用基于正弦型加加速度的七段式路徑，對航天器三軸姿態機動路徑進行規劃。這里以滾動軸為例，說明其具體思路。航天器的角加加速度曲線由正弦函數組成，對其進行三次積分，即得角位置曲線［10］。圖1為路徑規劃示意圖。

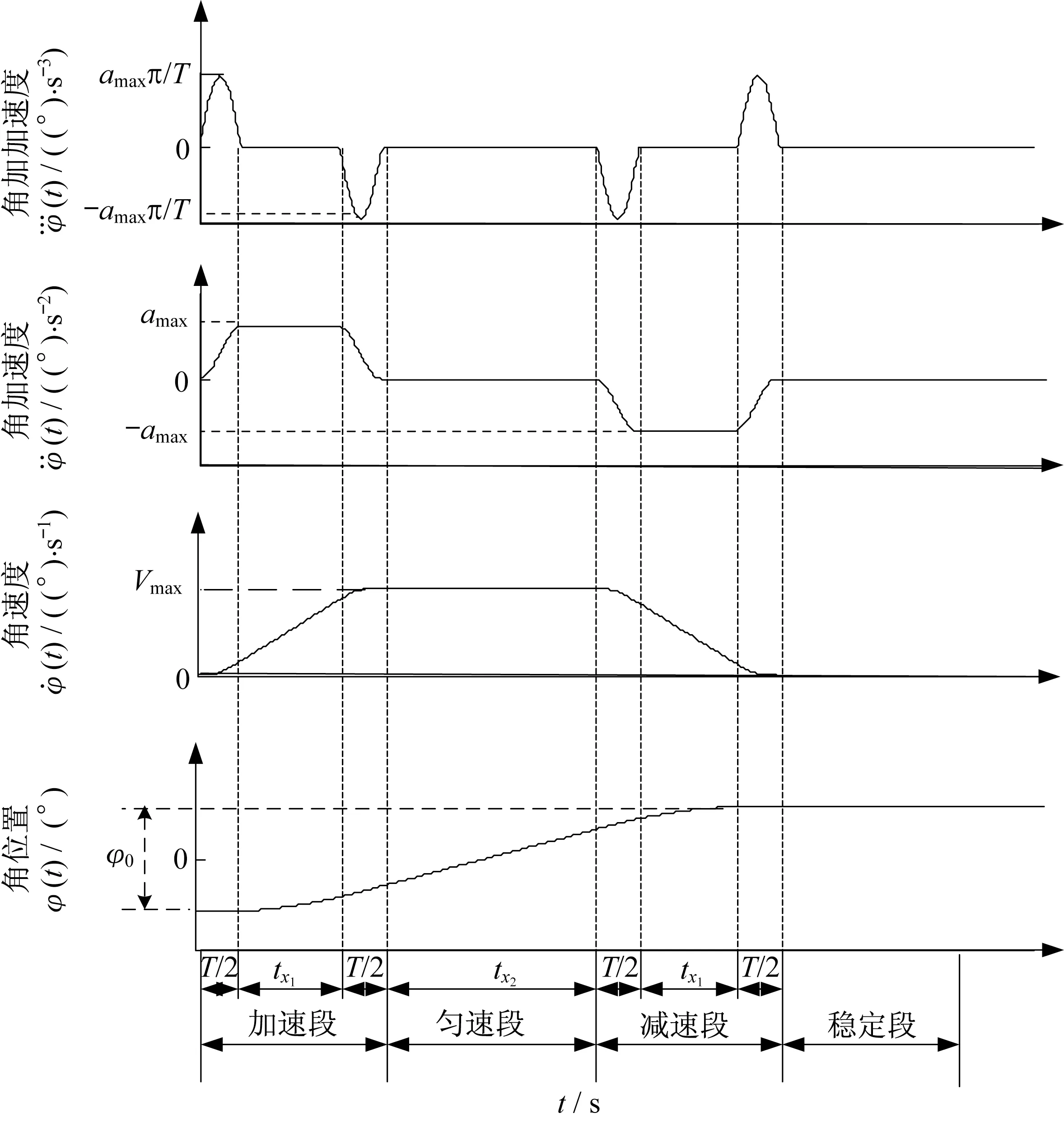
圖1 基于正弦型加速度的七段式路徑規劃示意圖Fig.1 The seven-segment path planning diagram based on the sinusoidal acceleration

要求充液撓性航天器的滾動軸從0 機動到φ0，圖1中，Vmax和amax分別為航天器滾動軸可達到的最大角速度和角加速度（考慮實際航天器姿態三軸角速度測量元件的測量范圍有限，設定Vmax和amax不超過實際系統允許的最大速度Vsystem_max和最大加速度asystem_max），T為正弦函數的周期，tx1為第2 段（勻加速段）和第6 段（勻減速段）的時間，tx2為勻速段的時間。

當航天器姿態機動角度和最大角速度確定后，通過調節角加速度和正弦函數的周期，按照tx1=確定機動路徑的參數。七段式機動路徑的表達式如下：

第1 段（t≤T/2）

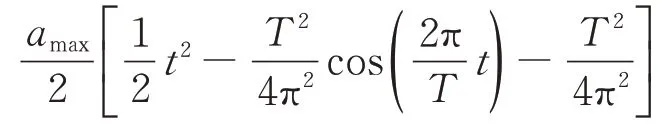
第2 段（T/2 ＜t≤T/2+tx1）

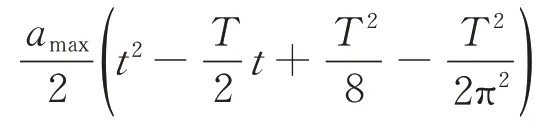
第3 段（T/2+tx1＜t≤T+tx1）

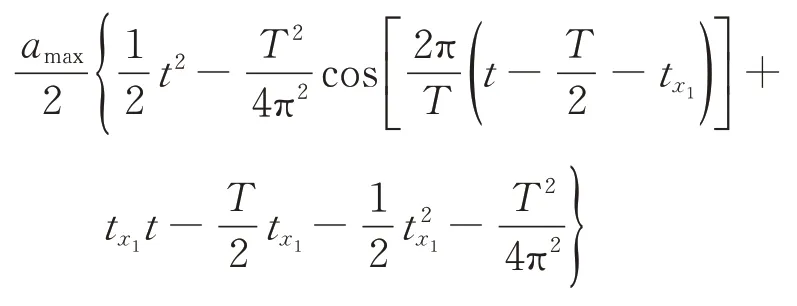
第4 段（T+tx1＜t≤T+tx1+tx2）

第5 段（T+tx1+tx2＜t≤3T/2+tx1+tx2）

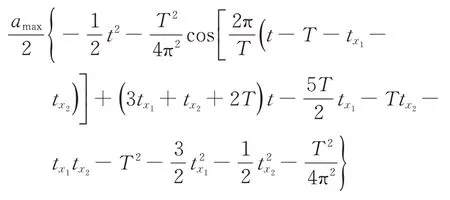
第6段（3T/2+tx1+tx2＜t≤3T/2+2tx1+tx2）

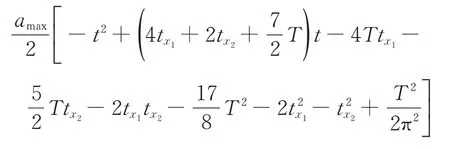
第7段（3T/2+2tx1+tx2＜t≤2T+2tx1+tx2）

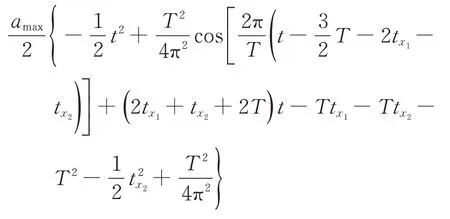
穩定段（t＞2T+2tx1+tx2）

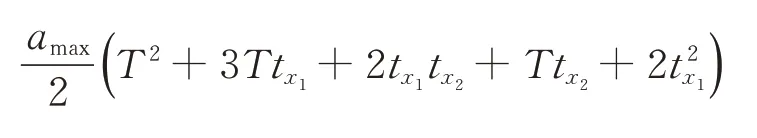
1.3 姿態控制器

為了減小航天器姿態機動對液體晃動和撓性附件振動的激發，實現快速機動、快速穩定的控制目標，采用反饋控制器與機動路徑規劃相結合的姿態控制方案，系統結構如圖2 所示。

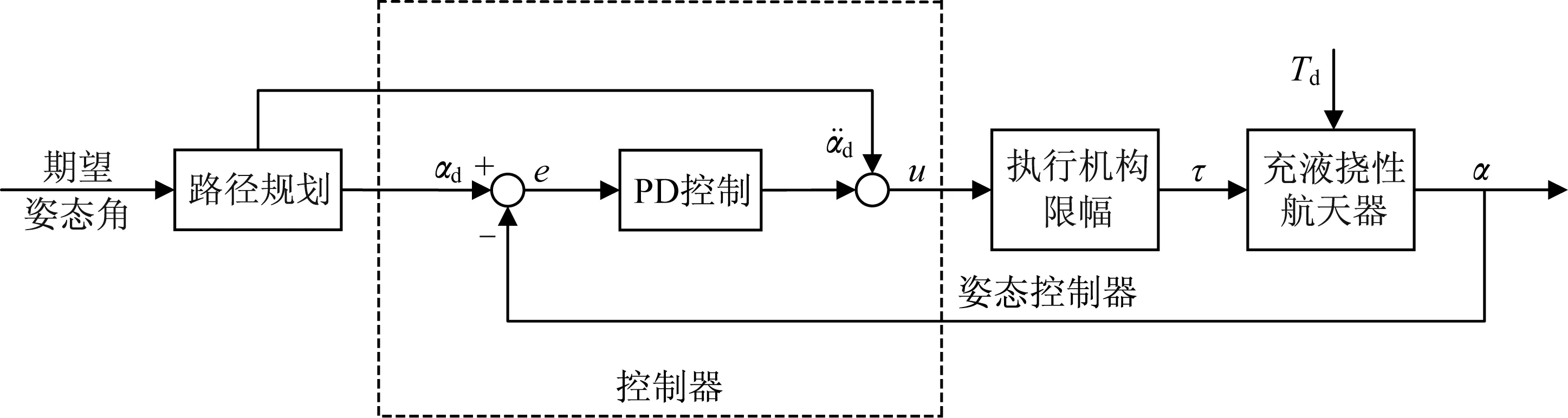
圖2 充液撓性航天器姿態控制系統結構Fig.2 The structure of the attitude control system for a liquid-filled flexible spacecraft

圖2中，αd、分別為期望 的角位置、角加速度向量，α為實際的姿態角向量，e=αd?α為姿態角誤差向量。圖2中姿態控制器采用微分先行的PD控制律，即

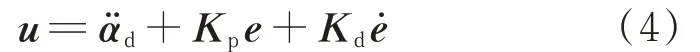
式中：Kp=diag(Kpx，Kpy，Kpz)為姿態控制器的比例控制系數矩陣；Kd=diag(Kdx，Kdy，Kdz)為微分控制系數矩陣；為角速度誤差向量。經執行機構輸出限幅后，作用到航天器上的控制力矩向量為

式中：ulimit為執行機構能夠輸出的最大控制力矩向量。

2 充液撓性航天器姿態機動路徑參數及控制器參數聯合優化

從航天器動力學模型式（1）～（3）可以看出：由于剛-柔-液耦合特性，航天器大角度姿態機動不僅會激發撓性附件的振動，而且還會激發液體燃料的晃動。同時，撓性附件振動和液體燃料晃動都會影響航天器的姿態控制性能。

航天器大角度姿態機動時，三軸姿態均需滿足快速機動、快速穩定的控制目標，但是各項指標之間常常存在矛盾，這是一個復雜的多目標優化問題，需要進行綜合優化，使各項指標盡可能好，而不僅僅是某個指標達到最優。此外，由于航天器三軸姿態運動的耦合作用，三軸姿態機動的路徑參數及控制器參數均會影響姿態機動的控制性能，如果僅對機動路徑參數進行優化，控制器的參數仍然難以選擇和優化。針對此問題，本文提出對充液撓性航天器的姿態控制器參數和機動路徑參數進行多目標聯合優化，以進一步提高姿態機動控制的性能。

云多目標粒子群優化（Cloud Multi-Objective Particle Swarm Optimization，CMOPSO）算法是一種改進的粒子群優化算法，它利用外部粒子群引導群體外粒子的飛行，保存非劣解，利用自適應網格法來維護外部粒子群，從而平衡算法的全局搜索能力和局部搜索能力［12］。CMOPSO 算法具有搜索速度快、效率高、算法簡單、能夠實現多個目標同時優化等特點，可以較好地解決普通粒子群算法易陷入局部最優的問題，故本文采用CMOPSO 算法對航天器的姿態控制器和路徑參數進行聯合優化。

充液撓性航天器滾動、俯仰和偏航三軸需優化的姿態機動路徑參數分別為三軸機動路徑的角加速度的最大值amax_x、amax_y、amax_z和三軸正弦函數的周期Tx、Ty、Tz，需優化的三軸姿態控制器參數為比例系 數Kpx、Kpy、Kpz和微分系 數Kdx、Kdy、Kdz。假 設三軸姿態角達到指定的指向精度pt的時間為f1x、f1y和f1z，三軸穩定度記為f2x、f2y和f2z。姿態機動控制聯合優化的目標是使f1x、f1y、f1z、f2x、f2y、f2z同時達到盡可能小的值。為此，建立充液撓性航天器姿態機動路徑參數和控制器參數聯合優化模型，求取ζ=[amax_y，amax_z，Tx，Ty，Tz，Kpx，Kpy，Kpz，Kdx，Kdy，Kdz]，使得

其中，ζ需滿足以下約束條件：

1）Kp·∈[Kp·_min，Kp·_max]，其中，Kp·_min、Kp·_max（·=x，y，z，分別代表航天器的滾動軸、俯仰軸以及偏航軸）為設計的航天器三軸姿控器中比例系數的最小值和最大值；

2）Kd·∈[Kd·_min，Kd·_max]，其中，Kd·_min、Kd·_max（·=x，y，z）為設計的航天器三軸姿控器中微分系數的最小值和最大值；

3）amax_·∈(0，amax]（·=x，y，z），其中，amax為規劃的姿態機動路徑中的最大角加速度的絕對值；

4）設tmax為由姿態機動指標確定的最大機動時間，則 有2T(·)+2t(·)1+t(·)2∈(0，tmax]，(·=x，y，z)，其中，T(·)(·=x，y，z)為三軸機動路徑中正弦函數的周期，t(·)1，t(·)2(·=x，y，z)分別為三軸姿態機動路徑勻加（減）速段的時間和勻速段的時間；

5）規劃的三軸姿態角在t(·)=2T(·)+t(·)1+t(·)2時達到φ(·)0，φ(·)0（·=x，y，z）為設計的航天器三軸的指定機動角度。

在以上限制條件下，聯合優化控制器參數和路徑參數，得到式（5）的多目標Pareto 解集。CMOP?SO 聯合優化算法流程如圖3 所示。

3 仿真試驗及結果分析

3.1 本文算法仿真結果

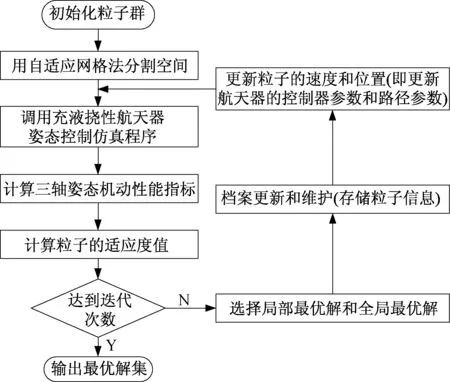
圖3 基于CMOPSO 的參數聯合優化算法流程圖Fig.3 Flow chart of the parameter joint optimization algorithm based on the CMOPSO

仿真用充液撓性航天器的數學模型及參數取自文獻［11］。充液撓性航天器初始姿態角為［?30，0.5，0.5］（°），期望達到的姿態角為［30，0，0］（°），三軸初始姿態角速度均為10?3（°）/s。姿態機動采用基于正弦型加加速度七段路徑，并利用CMOP?SO 聯合優化充液撓性航天器姿態機動路徑參數和控制器參數。考慮實際航天器姿態三軸角速度測量元件的測量范圍有限，設定機動路徑的勻速段角速度限幅為Vsystem_max=2.5（°）/s，角加速度限幅為asystem_max=0.4（°）/s2，控制器力矩 限幅為ulimit=25 N·m，系統采樣時間為0.05 s。

性能指標：當充液撓性航天器滾動軸機動60°時，考慮三軸運動耦合，為了平穩進行姿態機動，對俯仰軸和偏航軸亦按照所設計的七段路徑進行規劃，要求三軸姿態機動時間控制在tmax=70 s 之內，指向精度優于pt=0.005°；且在100～150 s（穩定時間）內，穩定度優于6×10?5（°）/s。

本文算法只需運行一次，即可得到多組充液撓性航天器姿控參數聯合優化Pareto 解（即優化的路徑參數和控制器參數），其中兩組Pareto 解見表1。將這兩組Pareto 解應用到充液撓性航天器的機動路徑和控制器中，對應的姿態機動性能指標見表2。

選取Pareto 解2 用于充液撓性航天器的系統模型中，參數聯合優化仿真結果如圖4 所示。

由表2 可以看出：充液撓性航天器的控制器參數和機動路徑參數經過CMOPSO 聯合優化后，得到的這兩組Pareto 解都可以使得航天器在49.25 s內完成滾動軸機動60°的機動任務。

表1 基于CMOPSO 算法的姿控參數聯合優化Pareto 解Tab.1 The optimized Pareto solutions of joint attitude control parameters based on the CMOPSO

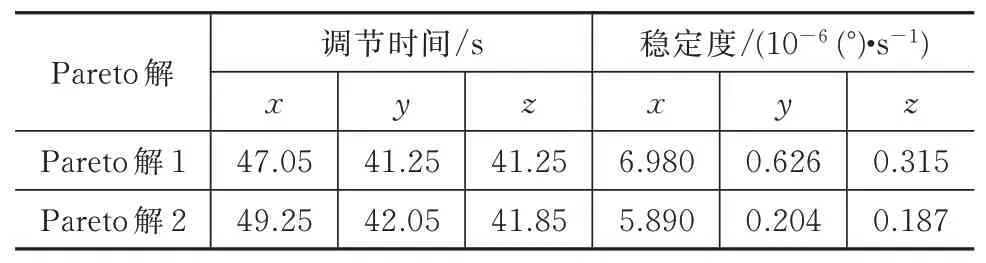
表2 參數優化所得Pareto 解對應的性能指標Tab.2 Performance indexes of the Pareto solutions obtained by the parameter optimization

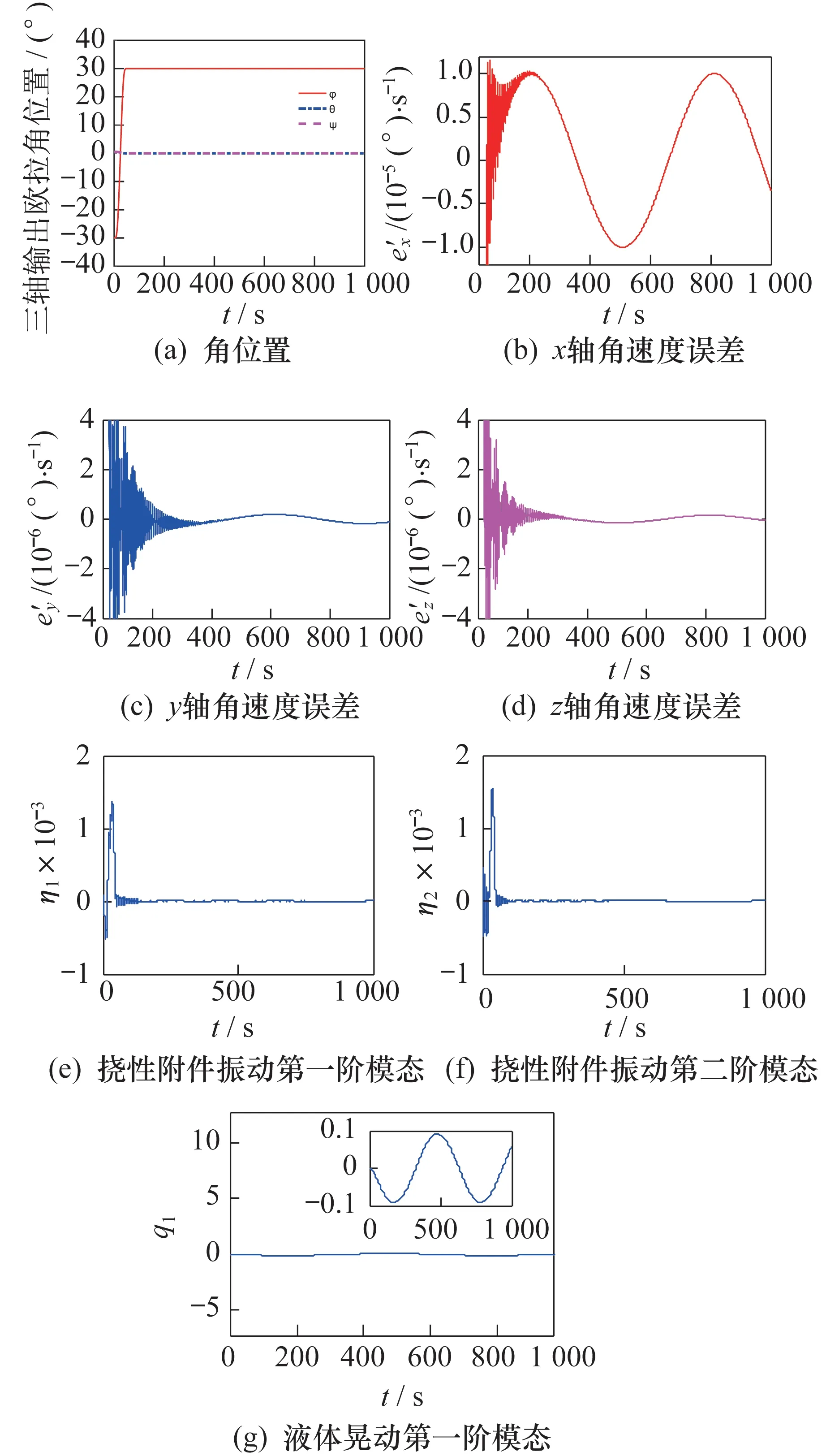
圖4 充液撓性航天器參數聯合優化仿真結果Fig.4 Simulation results of the joint optimization of parameters for the liquid-filled flexible spacecraft

結合表2 和圖4 可以看出：達到穩定狀態后，航天器三軸角位置均達到期望的指向精度和穩定度，并且三軸姿態穩定度均可達到10?6（°）/s 的數量級。對比表2中的兩組Pareto 解可以看出：Pareto 解1 的調節時間比Pareto 解2 略短，但穩定度較Pareto 解2略低，兩組解各有優點，互不支配。由圖4（e）、圖4（f）可以看出，撓性附件一、二階振動模態幅值均約為0.001 5。由圖4（g）可以看出，液體晃動模態（僅考慮第一階模態）幅度約為0.1。由此可見，采用本文所提聯合優化算法搜索得到的機動路徑參數和控制器參數，能使充液撓性航天器完成快速機動、快速穩定的控制目標。

3.2 與其他方法比較

充液撓性航天器在完成大角度姿態機動的任務時，三軸姿態均需滿足快速機動、快速穩定的控制目標，并且由于航天器三軸姿態運動的耦合作用，三軸姿態機動的路徑參數及控制器參數對姿態機動的控制性能的影響均不容小覷。若只考慮控制器參數對航天器控制性能的影響，不采用本文給出的姿態機動路徑規劃方法，而直接令滾動軸從初始姿態?30°階躍至30°，俯仰軸和偏航軸均從初始姿態角度0.5°階躍至0°，控制器參數采用3.1 節中優化后的Pareto 解2中的控制器參數，獲得的航天器姿態機動控制的性能指標如下：三軸調節時間為416.05、419.90、391.50 s，三軸穩定 度為1.450 6、1.519 7、1.380 8（°）/s。姿態階躍響應仿真結果如圖5 所示。

圖5 充液撓性航天器姿態階躍響應仿真結果Fig.5 Simulation results of the attitude step responses of the liquid-filled flexible spacecraft

結合圖4 與圖5 可看出：采用了聯合優化算法獲得的姿控參數后，航天器的三軸調節時間縮短了大約360 s，三軸穩定度提高了約10?5倍。總之，采用了聯合優化算法獲得的姿控參數后姿態機動控制的性能指標均大大優于姿態階躍機動控制的性能指標。再考慮撓性附件振動強度和液體晃動幅度，對比圖4 和圖5 可以看出：采用聯合優化算法后撓性附件振動第一、二階模態幅值縮小到原來的1/330，液體晃動第一階模態幅值縮小到原來的1/60，聯合優化算法顯著抑制了撓性附件振動和液體晃動。綜上，采用了本文設計的聯合優化算法搜索得到的機動路徑參數和控制器參數后，航天器的姿態控制性能均有較大提高，并且撓性附件振動和液體晃動亦得到非常有效的抑制，從而驗證了聯合優化算法的有效性。

4 結束語

本文針對一類帶液體燃料和撓性附件的航天器快速機動、快速穩定的控制要求，研究了一種姿態機動路徑優化方法，將微分先行的PD 姿態控制器與基于正弦型加加速度的七段路徑規劃相結合，并采用CMOPSO 算法聯合優化充液撓性航天器姿態控制器參數及機動路徑參數。仿真結果表明：采用本文所提聯合優化算法的姿控參數能夠顯著減小液體晃動和帆板振動對航天器的影響，使充液撓性航天器能夠較好地完成大角度姿態快速機動、快速穩定的任務。目前本文在姿態機動角度已知的情況下，研究了航天器姿態機動路徑及參數優化的問題，由于計算量較大，只能離線優化。未來將進一步研究更為有效的在線優化方法，從而實時規劃航天器機動路徑，以適應更為復雜的航天任務要求。