一種考慮攝動影響的星座構型穩定性設計方法
陳長春,林 瀅,沈 鳴,戴光明,王茂才
(1.上海衛星工程研究所,上海 201109;2.中國長城工業集團有限公司,北京 100054;3.中國地質大學 計算機學院,湖北 武漢 430074)
0 引言
衛星星座在運行過程中,受到地球非球形攝動、太陽光壓和大氣阻力等攝動力的影響,會慢慢偏移其標稱軌道,進而使星座整體構型被破壞,星座性能降低,影響到衛星星座穩定性[1]。
Walker 星座由于其獨特的構型,在通訊、定位、海洋、軍事等領域起到了至關重要的作用[2]。隨著工程需求的提高,對Walker 星座的精確度要求不斷提高,研究考慮各種攝動模型后的精確Walker 星座發射以及Walker 星座在長期工作運行中如何進行星座穩定性設計,從而保證星座構型穩定性,已成為研究熱點[3]。
在對Walker 星座構型穩定性方案進行分析時,需對各種攝動模型進行精確建模,分析不同攝動力對衛星軌道的影響[4-5]。考慮攝動模型下,在一個典型的Walker 星座進行部署時,由于星座中各顆衛星發射時間的區別,其所受的攝動力的時間累積效應也有所差別[6],因此,需要消除在該累積效應帶來的影響量[7]。在建立標準Walker 星座后,結合Walker星座構型特性,分析其衛星軌道在攝動模型下產生的運動軌跡變化趨勢[8-9],研究設計星座構型保持策略,以實現保持星座構型穩定性的目的[10]。
1 設計思路
根據Walker構型整體對稱的特性[11],若對星座中所有衛星的緯度幅角和升交點赤經都改變ΔΩ與Δλ,星座的整體構型將不會受到影響,仍然會保持穩定。
編號為i的衛星在考慮各種攝動下的軌道命名為Si,在t時刻其升交點赤經和緯度幅角分別命名為Ωi(t)和λi(t),其標稱軌道命名為,在t時刻標稱軌道升交點赤經和緯度幅角分別命名為(t)和(t),則在t時刻,Si與的升交點赤經和緯度幅角之差為
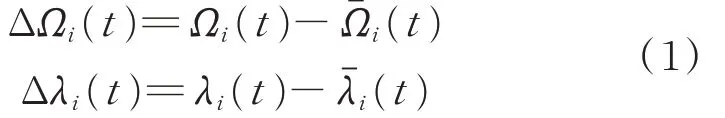
由式(1)計算得到的偏差稱為實際軌道與標稱軌道的絕對偏移量。
在t時刻整個星座的升交點赤經之差與緯度幅角之差被定義為星座中所有衛星升交點赤經差和緯度幅角差的平均值,即
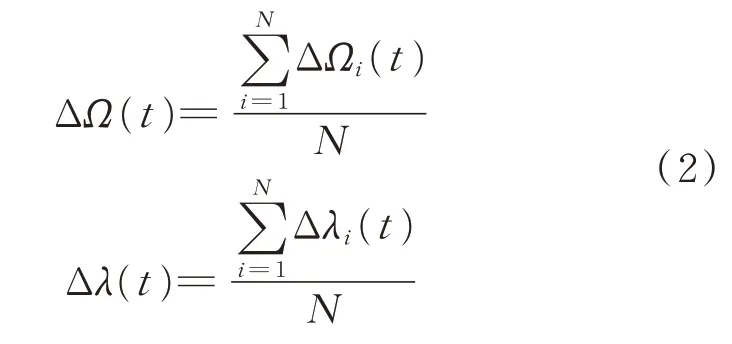
式中:N為星座中衛星的總數目。
由式(2)得到的結果稱為實際星座與標稱星座的平均偏移量,記
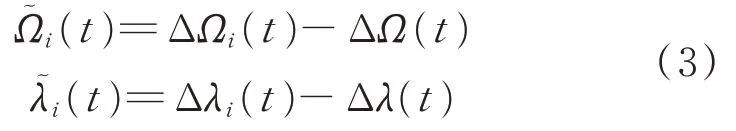
為每顆衛星的獨立偏移量。
根據式(3),可以計算得到每個時刻的升交點赤經和平均緯度幅角的獨立偏差為以及
根據每顆衛星的獨立偏差分別對軌道參數進行調整,若調整后其短周期項波動范圍在允許最大偏移量范圍內,則衛星在軌期間不需要再進行調整即滿足任務要求,否則需要在軌調整。
2 星座構型穩定性設計方法
2.1 半長軸影響分析
根據星座保持原理,進行軌道修正。為了與文獻[12]中的數據進行對比分析與驗證,所有參數選取與文獻中的數據相同,具體參數見表1。縮水,攝動模型只考慮非球形模型,且先對第一顆衛星進行分析。

表1 MEO 衛星星座構型Tab.1 Configuration of the MEO satellite constellation
通過實驗發現:采用CSTK 和STK 數值所計算的Ω1的線性項與理論公式中的Ω1的值整體斜率吻合,如圖1 所示;但采用CSTK 和STK 數值所計算的λ1的線性項與理論公式中的λ1的值整體斜率無法重合,如圖2 所示。圖中,橫坐標為MJD2K 時間歷元,即從2000年1 月1 日00∶00∶00 起算的時間歷元,時間增加1 d,MJD2K 的數字增大1,縱軸為角度偏移量。
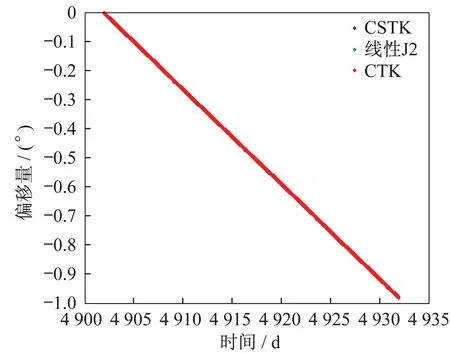
圖1 升交點赤經偏移量(1 個月)Fig.1 The offset of the right-ascension-of-ascending-node(one month)
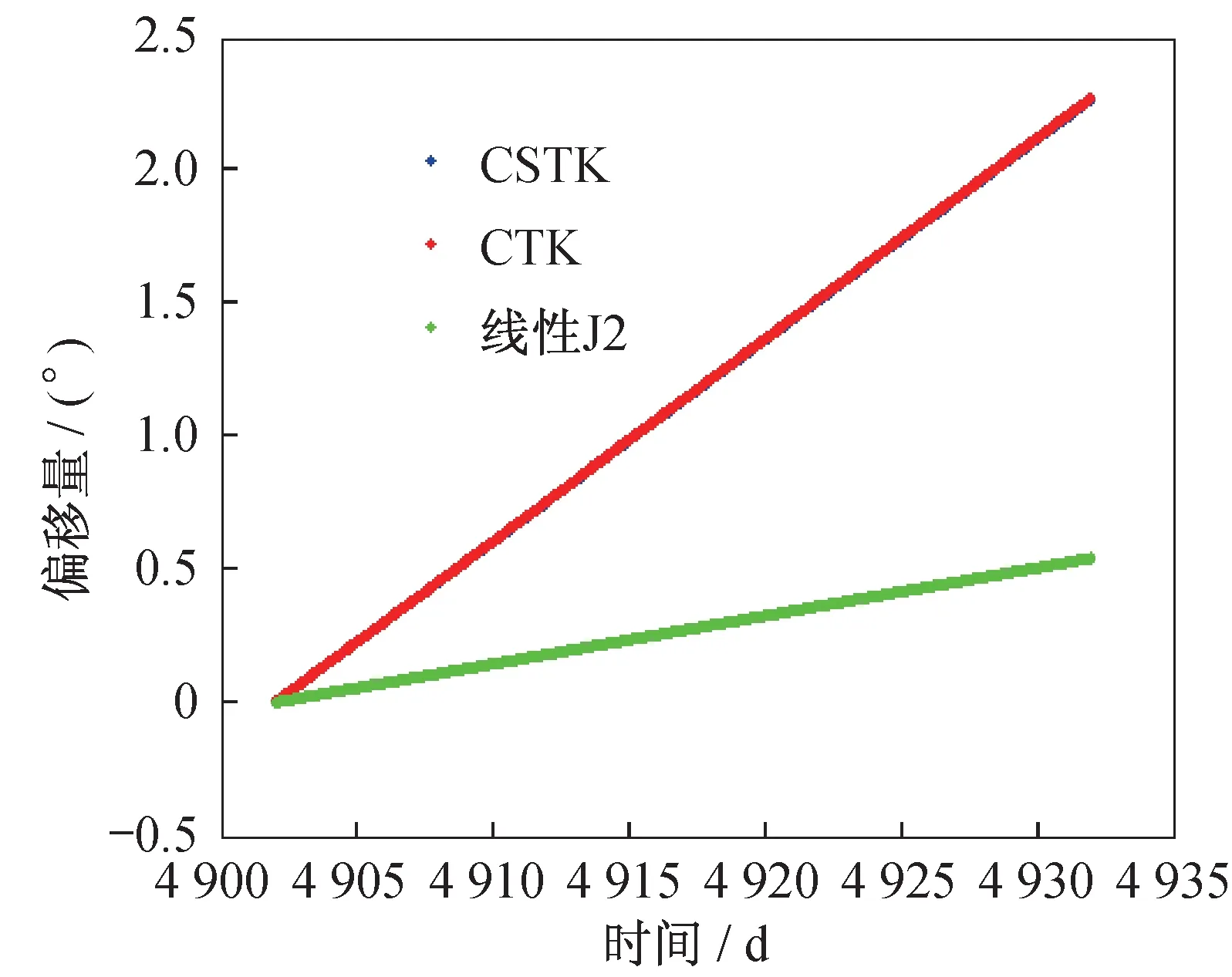
圖2 相位角偏移量(1 個月)Fig.2 The offset of the phase angle(one month)
實驗中,CSTK 和STK 數值所計算的λ1的線性項與理論公式中的λ1的值整體斜率無法重合,而在使用影響矩陣A獲得需要調整的軌道半長軸和軌道傾角時需要用到理論λ1的值,因而結果會出問題。經過實驗與分析得知,產生這個問題的原因在于半長軸的短周期項的影響。實驗中,STK 非球形攝動模型下半長軸偏移量隨時間變化如圖3 所示。

圖3 非球形攝動下半長軸偏移量Fig.3 The offset of the semi-major axis under nonspherical perturbation
從圖3中看到衛星的半長軸是隨時間變化的,需要考慮半長軸長期項的影響為
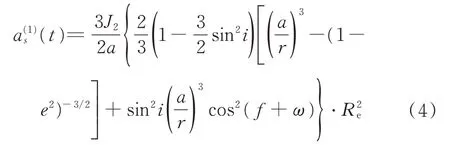
式中:Re為地球半徑,其數值取6 378.137;a、e、i、ω與f分別為衛星的半長軸、偏心率、軌道傾角、近地點俯角和真近點角;r為衛星到地心的距離;J2為地球的非球形效應的二階帶諧項系數。
根據實際問題,簡化后為
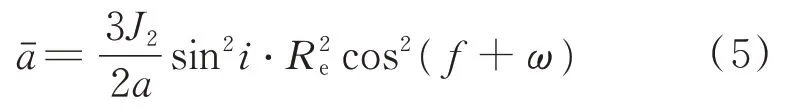
因而第一顆衛星的半長軸長期項影響計算為1.590 010 114 820 334 1,將實驗數據帶入STK 重新進行計算分析,結果如圖4 所示。考慮到半長軸長期項的影響后,STK 數值所計算的λ1的線性項與理論公式中的λ1的值整體斜率相互吻合。
2.2 衛星星座穩定性構型設計流程
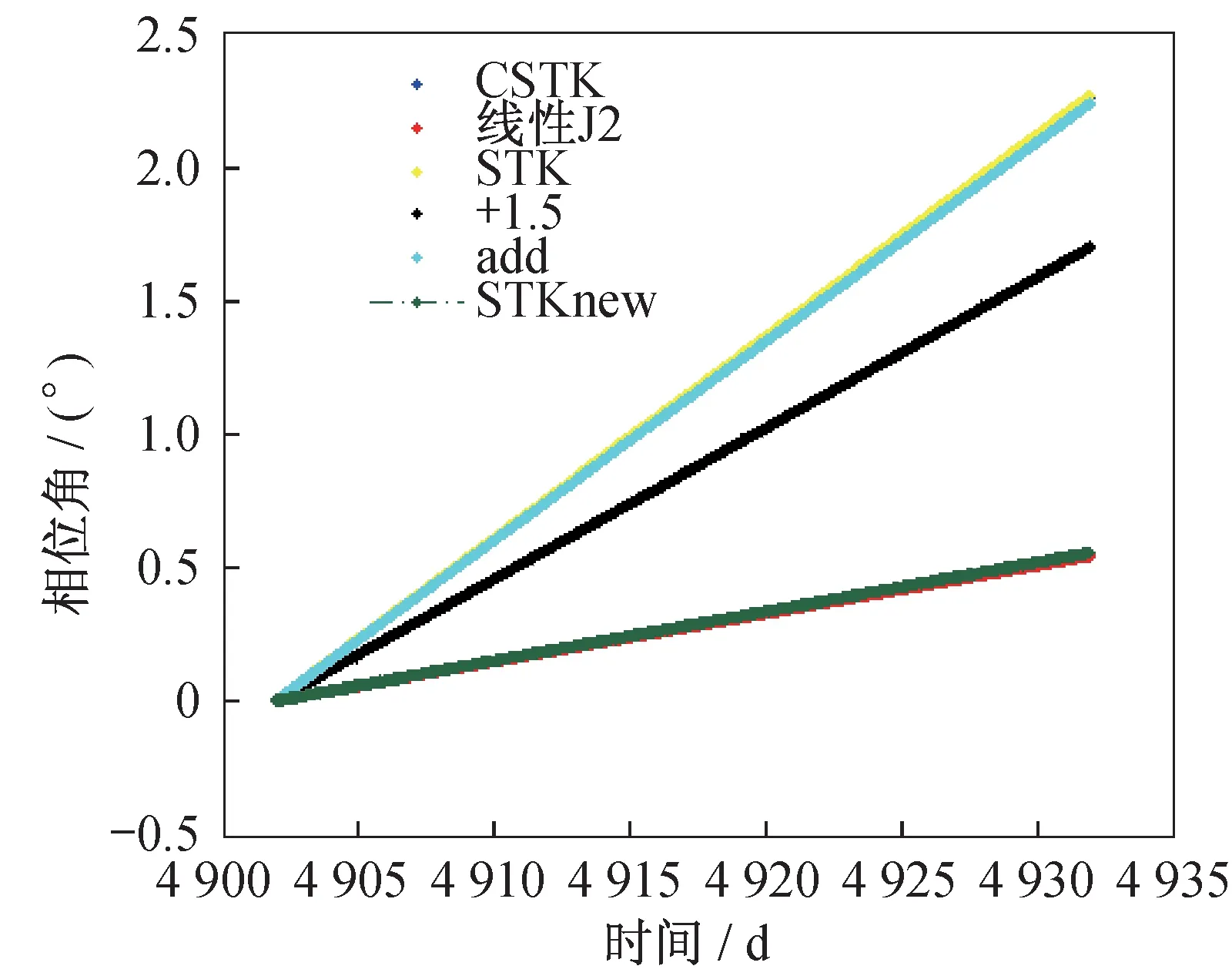
圖4 由實驗數據獲得的相位角偏移量(1 個月)Fig.4 The offset of the phase angle obtained with the experimental data(one month)
通過實驗分析,在消除衛星軌道因軌道半長軸短周期項的影響后,考慮多種攝動因素下,采用衛星星座整體偏移和數據擬合思想來設計星座構型穩定性保持策略,具體步驟如下:
步驟1消除星座衛星軌道因軌道半長軸短周期項的影響;
步驟2計算同時帶3 種攝動模型的星座中各顆衛星的升交點赤經絕對偏移量和相位角絕對偏移量;
步驟3根據衛星星座整體偏移原理,計算出每顆衛星的獨立偏移量;
步驟4對衛星星座中各顆衛星的獨立偏移量進行數據擬合,并根據參數偏置攝動補償原理計算出各顆衛星需要調整的半長軸的主動偏置量Δa和軌道傾角主動偏置量Δi;
步驟5對偏置后的衛星星座進行仿真測試,判斷是否已完全消除攝動對其產生的長期影響,以達到保持星座構型穩定性的目的,若還沒有消除,則轉步驟4,否則轉步驟6;
步驟6結束。
3 仿真試驗及結果分析
3.1 衛星參數
由于考慮到不同軌道高度攝動因素對衛星軌道的影響不同,特別是軌道高度的影響,為了驗證調整方案同樣適用于其他類型Walker 星座,實驗選取了一組中軌道高度的衛星數據進行實驗測試,具體參數見表2。

表2 衛星星座參數Tab.2 The parameters of the satellite constellation
3.2 測試結果及分析
首先獲得星座40 顆衛星的所有偏移量,考慮到前面提到的軌道半長軸的長期項,計算出各顆衛星開始前軌道半長軸的長期項影響量,消除其半長軸長期項的影響;然后再計算出每一時刻星座的平均偏移量,對其進行擬合,由于每顆衛星偏移量較大,擬合只選取具有代表特征的前45 d 的數據進行擬合。
通過前45 d 的數據進行擬合修正后,得到的修正后的星座,相位角和升交點赤經偏移量隨時間的變化曲線分別如圖5 和圖6 所示。
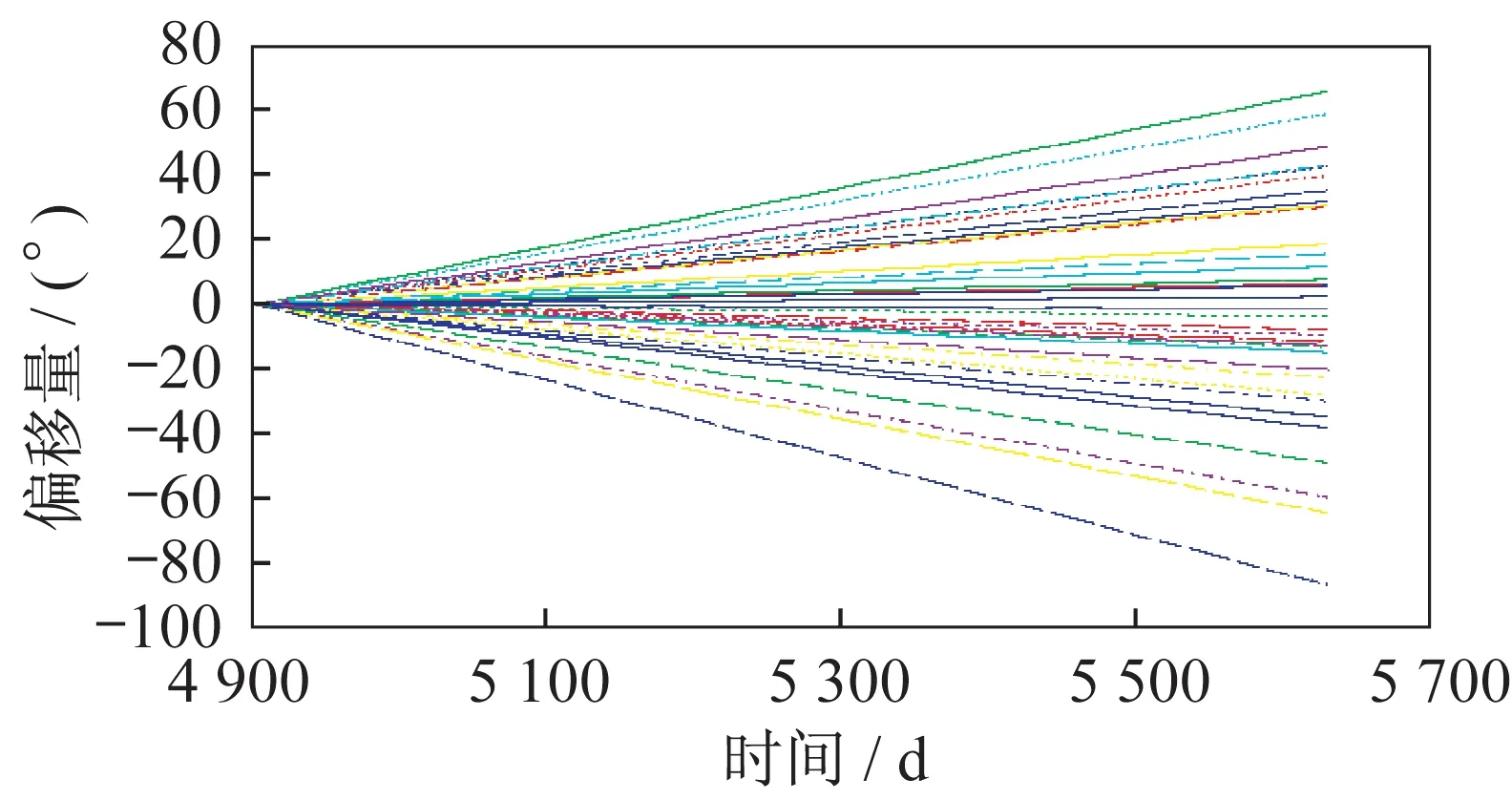
圖5 40 顆衛星各自相位角獨立偏移量Fig.5 The independent offsets of the phase angles of 40 satellites

圖6 40 顆衛星各自升交點赤經獨立偏移量Fig.6 The independent offsets of the right-ascension-ofascending-nodes of 40 satellites
由圖5 可知:40 顆衛星的相位角仍然存在一個較大的隨時間增加的一個線性項,在2年時間內,最大相位角偏移量約為63°。
如圖6 所示,通過星座整體偏移,基本上已經消除了升交點赤經偏移量的線性項影響,但部分衛星仍然存在一個非常微小的線性項。
以上可知,攝動因素在2年內對衛星軌道的升交點赤經和相位角產生非常大的影響,使星座整體結構變形,若對其不進行星座控制保持策略,在短時間內即會超過星座的最大容許偏移量,使星座構型整體失效,不能達到預期的目的。
圖5 和圖6中的結果形成的原因,主要是升交點赤經偏移量和相位角偏移量由于攝動因素存在長期項外,還存在短周期項,在數據擬合過程中,可能無法通過一次數據擬合就十分準確表示其偏移量的變化量,因而需要進行第二次擬合調整。
將第二次修正調整后的軌道參數重新代入STK中進行計算檢驗,計算數據經過轉換后實際偏差量如圖7 和圖8 所示。
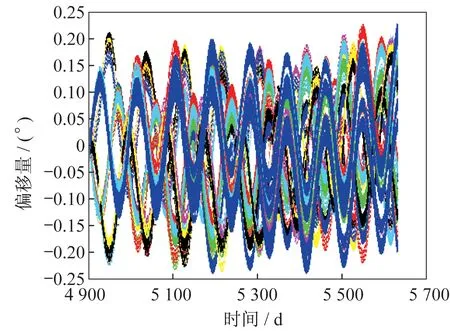
圖7 二次修正后40 顆衛星相位角偏移量Fig.7 The offsets of the phase angles of 40 satellites after the secondary correction
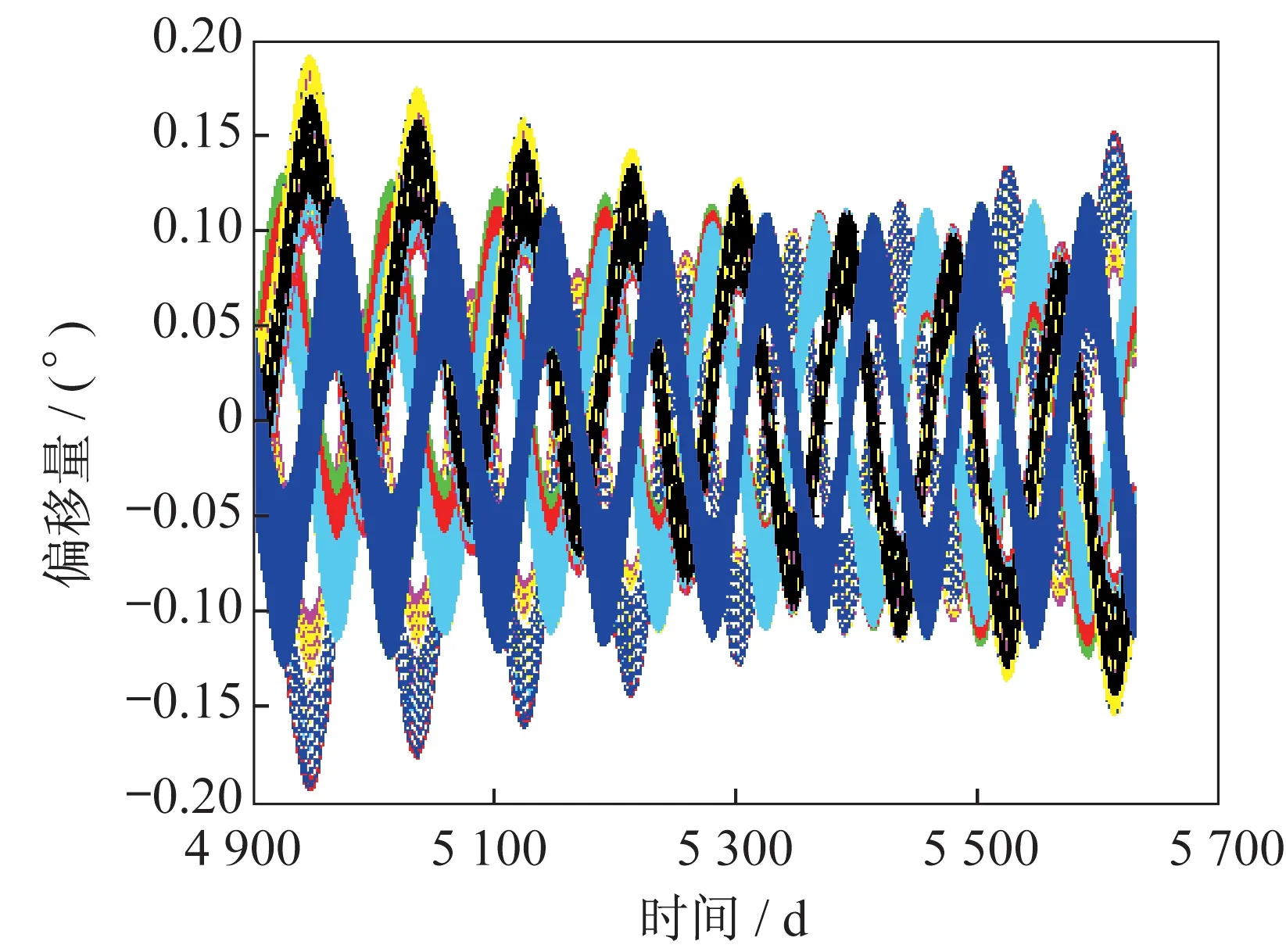
圖8 二次修正后40 顆衛星升交點赤經偏移量Fig.8 The offsets of the right-ascension-of-ascendingnodes of 40 satellites after the secondary correction
由圖7 和圖8 可知:40 顆衛星的相位角和升交點赤經偏移量在2年時間內,最大偏差都非常小,相位角的偏差不超過0.25°,升交點赤經的偏差不超過0.20°,而且兩者均不存在線性項效應。
通過計算可知,該星座對應的最大容許相位角偏移量為1°,最大容許升交點赤經偏移量也為1°,則該Walker 星座的偏差在最大容許偏差范圍之內。因此,可以得到結論:在考慮各種形式的攝動力效應下,該Walker 星座在2年時間內構型是穩定的。該數值仿真實驗也表明了數據擬合方法能有效地消除攝動對衛星軌道長期項影響,僅通過調整后的衛星軌道能在較長時間內保持其整體穩定性,達到了星座構型保持的目的。
4 結束語
本文對星座構型的最大容許偏移量進行分析計算,以此作為星座構型穩定性策略是否有效的衡量標準。在對衛星星座受到的攝動模型建模后,通過對攝動模型對衛星軌道的影響的深入分析實驗,提出了采用曲線擬合中的最小二乘法來分析和調整衛星初始軌道,并提出了星座整體偏移方法,結合衛星參數初始軌道偏置補償原理來獲得保持星座構型穩定性的目的。在設計了對應的星座構型穩定性策略后,對于所需要進行的衛星軌道的調整量,根據調整所需要的能量,從節省能源的角度出發,采用脈沖調整的方案進行機動變軌。最后通過實驗驗證了整套設計方案的可行性和高效性。

