基于變剛度變阻尼的柔性噴管動態模型

胡嘉鑫，薛牧遙，楊敬賢，童 悅，鄒 杰，鄭 慶，任軍學

（1.北京航空航天大學 宇航學院，北京 100191；2.上海航天動力技術研究所，上海 200125）

0 引言

柔性噴管主要由活動體、固定體、柔性接頭等部件組成［1］，其與伺服系統共同構成推力矢量控制系統［2］，主要應用于高過載機動飛行的防空導彈及反導導彈中［3-4］。柔性噴管的動態特性主要由柔性接頭和伺服系統決定。由于實現擺動的柔性接頭中的橡膠材料的黏彈性和摩擦性，柔性噴管在受正弦激勵力作用做正弦擺動時，其恢復力矩-擺角曲線會出現遲滯現象，形成遲滯曲線。遲滯曲線受柔性接頭工作壓強、工作溫度、擺動振幅、擺動頻率，以及橡膠材料性能等多方面因素的影響［5-6］，使柔性噴管的動態特性變得十分復雜，模型難以將各個因素均考慮在內，影響了控制系統的控制精度［7］。針對柔性接頭動態特性問題，通常將柔性接頭視作簡單的質量-彈簧系統［8］（定剛度定阻尼模型），未考慮擺動振幅、擺動頻率對剛度系數和阻尼系數的影響，無法反映遲滯曲線的變化趨勢。Naupapac等［9］使用查表法作為柔性接頭的運動模型，但只適用于某一振幅下某一頻率的遲滯曲線；鄭開發等［10］提出了剛度系數可變、阻尼系數可變的柔性接頭運動模型，可以預測某一振幅下不同頻率的恢復力矩。此外可借鑒橡膠隔振器的研究方法，Markou等［11］將隔振器視為非線性彈簧、彈塑性模塊、遲滯阻尼器的組合，可以預測隔振器在同一頻率下不同振幅的遲滯曲線，但不能預測同一振幅下不同頻率的遲滯曲線。龔憲生等［12］考慮到了隔振器存在的黏性阻尼、干阻尼以及高階阻尼，構建了新的阻尼模型，該模型能夠清晰地反映隔振器中阻尼的組成成分及其大小，但對信噪比要求高，參數識別困難。上述研究對柔性接頭的動態模型很有借鑒意義，但除了文獻［8］中的定剛度-定阻尼模型和文獻［9］中的查表法模型之外，其余研究均未結合伺服機構模型進行研究。

為了更準確模擬柔性接頭的遲滯特性，并明確電液伺服機構和柔性接頭在系統中的作用，本文將基于柔性接頭變剛度-變阻尼模型構造電液伺服機構-變剛度變阻尼模型，與電液伺服機構-定剛度定阻尼模型進行了對比，并研究電液伺服機構不同參數和柔性接頭工作參數對模型的影響。

1 柔性接頭動態實驗

柔性接頭的實驗裝置如圖1 所示。該裝置由高壓氣瓶向壓力容器填充高壓N2模擬柔性接頭的工作壓力，并通過電液伺服機構驅動作動器產生設定振幅，設定頻率的正弦激勵力，用于產生柔性接頭擺動所需要的擺動力矩。2 個水平安裝的位移傳感器用來測試柔性接頭的擺角，結合鉛垂的位移傳感器可測量柔性接頭的擺心［13］，拉壓力傳感器用于測試作動器所施加的作用力，在得出擺心和作動力后，按照文獻［1］所提到的方式即可計算出作動力矩。

圖1 柔性接頭實驗系統Fig.1 Experimental system for flexible joints

當工作壓力為9、6、3 MPa，柔性接頭擺動振幅為6°、5°、4°，頻率為0.1～1.0 Hz（間隔為0.1 Hz）時，分別測量了擺動力矩隨擺動角度的變化關系，即遲滯曲線，相關實驗結果如圖3（a）、圖4（a）、圖5（a）所示。柔性接頭變剛度變阻尼模型是在實驗結果的基礎上建立的，并進一步結合電液伺服機構模型構建了電液伺服機構-變剛度變阻尼模型。

2 電液伺服機構-變剛度變阻尼模型

2.1 變剛度變阻尼模型

將柔性接頭的擺動力矩分解為慣性力矩MI=其中，I為轉動慣量，δ為擺角），阻尼力矩Mc=Kr·，以及彈性力矩Mk=Kδ，其角運動符合二階非線性齊次微分方程，即

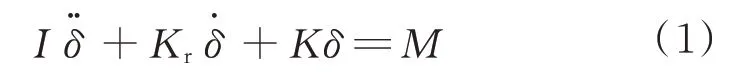
在之前的研究中，一般將柔性接頭簡化為剛度系數K和阻尼系數Kr不變的質量-彈簧系統（定剛度定阻尼模型），忽略了擺動振幅、擺動頻率、工作壓強、橡膠材料特性等對K、Kr的影響［8］。柔性接頭的定剛度定阻尼模型與遲滯曲線實驗結果吻合較差，且不能反映遲滯曲線隨頻率的變化趨勢（參見2.3 節）。本文采用了剛度系數與阻尼系數均可變化的模型（變剛度變阻尼模型）［10］，預測某一擺動振幅下不同擺動頻率的恢復力矩與擺角之間的關系。

在變剛度-變阻尼模型中，仍將恢復力矩M分解為彈性力矩Mk、阻尼力矩Mc、慣性力矩MI3 部分，所不同的是剛度系數可隨頻率f變化，彈性力矩為Mk=K0+K1·δ+K2·δ2+K3·δ3，阻尼系數也可隨頻率f變化，阻尼力矩為Mc=c·，

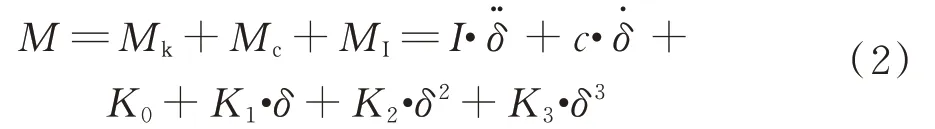
根據第1 節的試驗方法得到擺動力矩-擺角試驗數據后，在某一振幅下4 組不同頻率遲滯曲線實驗結果（頻率分別為0.1、0.4、0.7、1.0 Hz）的基礎上，運用最小二乘法對剛度系數和阻尼系數進行識別，可得到該振幅下剛度系數和阻尼系數關于頻率的函數關系，函數形式為

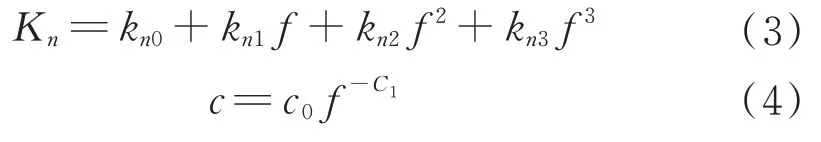
2.2 電液伺服機構

柔性噴管的動態特性不僅取決于柔性噴管本身，也取決于與之匹配的伺服系統［8，14］。本模型采用電液伺服系統作為柔性噴管的伺服系統。為方便分析，忽略電液伺服機構的非線性因素、結構變形、油泵動態、蓄能器影響等因素，所構建的信號綜合方程為

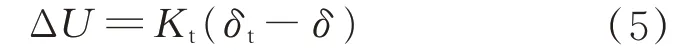
式中：δt為指令擺角；Kt為反饋系數；ΔU為誤差信號。

伺服器放大變換方程為

式中：Kui為放大器靜態放大系數；IV為放大器的輸出電流。

電液伺服機構一階傳遞函數為

式中：YV為閥芯的真實位移；Ks為電液伺服機構增益；ωs為電液伺服閥一階表現頻率。

流量分配方程［8］為

式中：δ為實際擺角；KQ為滑閥流量增益；A為作動器的活塞面積；R為力臂長度；PL為滑閥負載壓差；B為油液容積彈性模數；VT為受壓容積；Kce為總壓力流量系數。

結合柔性接頭變剛度變阻尼模型，由于電液伺服機構作動器所提供的力矩M=ARPL和柔性接頭變剛度-變阻尼模型的擺動力矩M=Mk+Mc+相等，則可得方程

結合式（5）～式（9）構建電液伺服機構-變剛度變阻尼模型，如圖2 所示。

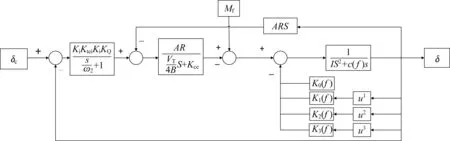
圖2 電液伺服機構-變剛度變阻尼模型示意圖Fig.2 Schematic diagram of the electro-hydraulic servo mechanism-variable stiffness and variable damping model

2.3 電液伺服機構-變剛度變阻尼模型與電液伺服機構-定剛度定阻尼模型的對比

擺動頻率對遲滯曲線影響如圖3 所示。圖3（a）為柔性接頭在不同擺動頻率作用下的遲滯曲線實驗結果。由圖3（a）可以看出：隨著頻率的增加，遲滯曲線所圍成的面積稍有增大，在0°擺角位置的力矩稍有增大，遲滯曲線沿順時針方向發生了轉動。圖3（b）為不同擺動頻率作用下的電液伺服機構-定剛度定阻尼模型遲滯曲線。由圖3（b）可以看出：隨著頻率的增加，遲滯曲線所圍成的面積大幅增加，在0°擺角位置的力矩也大幅增大，遲滯曲線不發生轉動，與圖3（a）實驗結果相差較大。圖3（c）為不同擺動頻率下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖3（c）可以看出：與電液伺服機構-定剛度定阻尼模型相比，電液伺服機構-變剛度變阻尼模型所構造的遲滯曲線可以更加準確地與實驗結果相吻合，并符合實驗結果隨頻率變化的規律。

3 柔性接頭工作參數對電液伺服機構?變剛度變阻尼模型的影響

為了明確柔性接頭工作參數對電液伺服機構-變剛度變阻尼模型的作用，需研究柔性接頭工作壓強、擺動振幅等參數對電液伺服機構-變剛度變阻尼模型遲滯曲線和動態響應的影響。

柔性接頭工作壓強對系統遲滯曲線影響如圖4所示。圖4（a）為柔性接頭在不同工作壓強下的遲滯曲線實驗結果。由圖4（a）可以看出：隨著柔性接頭工作壓強的增大，遲滯曲線所圍成的面積增大，在0°擺角位置的力矩增大，遲滯曲線沿順時針發生了轉動。圖4（b）為柔性接頭不同工作壓強作用下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖4（b）可以看出：電液伺服機構-變剛度變阻尼模型所構造的遲滯曲線可以準確地與實驗結果相吻合，并符合實驗結果隨壓強變化的規律。

擺動振幅對系統遲滯曲線影響如圖5 所示。圖5（a）為柔性接頭在不同擺動振幅作用下的遲滯曲線實驗結果。由圖5（a）可以看出：隨著擺動振幅的增大，遲滯曲線所圍成的面積增加，在0°擺角位置的力矩增大，并沿逆時針旋轉。圖5（b）為不同擺動振幅作用下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖5（b）可以看出：電液伺服機構-變剛度變阻尼模型所構造的遲滯曲線可以準確地與實驗結果相吻合，并符合實驗結果隨振幅變化的規律。

此外由圖4 還可以看出：電液伺服機構-變剛度變阻尼模型遲滯曲線的最大振幅及其對應的力矩相對遲滯曲線實驗結果較小一些。這是由于當有指令δc輸入，系統會產生與之相對應的跟隨輸出δ，跟隨輸出δ將產生慣性力矩MI、阻尼力矩Mc、彈性力矩MK，系統需要建立壓差力矩M=ARPL以平衡MI、Mc、MK之和，從而產生壓差PL，在流量壓力系數有限的情況下（Kce≠0），系統需產生一定的偏差Δδ=δ?δc用來彌補壓差PL所引起的流量變化，使得跟隨輸出δ相對指令輸入δc較小，電液伺服機構-變剛度變阻尼模型遲滯曲線最大振幅及其所對應的力矩相對實驗結果較小。圖5中擺動振幅對系統遲滯曲線影響的原因同理。

圖3 擺動頻率對遲滯曲線影響Fig.3 Effects of the oscillating frequency on the hysteresis curves

圖4 柔性接頭工作壓強對系統遲滯曲線影響Fig.4 Effects of the flexible joint working pressure on the hysteresis curves

4 伺服機構參數對電液伺服機構?變剛度變阻尼模型的影響

為了明確電液伺服機構對電液伺服機構-變剛度變阻尼系統的作用，需研究電液伺服機構反饋系數Kt、放大器靜態放大系數Kui、電液伺服機構一階表現系數Ks、電液伺服機構一階表現頻率ωs、滑閥流量增益KQ、作動器活塞面積A、力臂長度R等伺服機構主要參數對電液伺服機構-變剛度變阻尼模型遲滯曲線和動態響應的影響。由于電液伺服機構-變剛度變阻尼模型可簡化為圖2中的形式，則可將Kt、Kui、Ks、KQ視作KtKuiKsKQ，將A、R視作AR。

圖5 擺動振幅對系統遲滯曲線影響Fig.5 Effects of the oscillating amplitude on the hysteresis curves

圖6為KtKuiKsKQ增大為設定值的2 倍、保持不變以及縮小為設定值的1/2 后對系統動態特性的影響。圖6（a）為不同KtKuiKsKQ作用下的系統閉環幅頻特性曲線。由圖6（a）可以看出：隨著反饋系數Kt、放大器靜態放大系數Kui、電液伺服機構增益Ks、滑閥流量增益KQ的增加，帶寬變大，響應也隨之變快。圖6（b）為不同KtKuiKsKQ作用下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖6（b）可以看出：電液伺服機構-變剛度變阻尼模型遲滯曲線的最大振幅及其對應的力矩相對遲滯曲線實驗結果較小，且變小程度隨著Kt、Kui、Ks、KQ的增大而變小。圖6（c）為不同KtKuiKsKQ作用下的電液伺服機構-變剛度變阻尼模型動態響應曲線。由圖6（c）可以看出：隨著Kt、Kui、Ks、KQ的增大，響應速度變快，振蕩變劇烈，超調量增加，穩態誤差減小。由此可見，Kt、Kui、Ks、KQ對系統動態影響很大。

圖7為作動器活塞面積A與力臂長度R的乘積AR增大為設定值的2 倍、保持不變以及縮小為設定值的1/2 后對系統動態特性的影響。圖7（a）為不同AR作用下的系統閉環幅頻特性曲線。由圖7（a）可以看出：隨著作動器活塞面積A、力臂長度R的增加，帶寬變大，響應也隨之變快。圖7（b）為不同的AR作用下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖7（b）可以看出：隨著作動器活塞面積A、力臂長度R的增大，電液伺服機構-變剛度變阻尼模型遲滯曲線在振幅最大處的相對遲滯曲線實驗結果變寬。圖7（c）為不同作動器活塞面積A、力臂長度R作用下的電液伺服機構-變剛度變阻尼模型動態響應曲線。由圖7（c）可以看出：隨著作動器活塞面積A、力臂長度R的增大，響應速度變快，超調量、振蕩次數、調節時間、穩態誤差均減小。

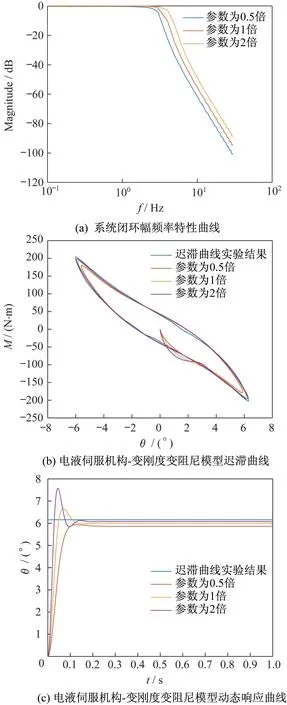
圖6 Kt、Kui、Ks、KQ對系統動態特性影響Fig.6 Effects of Kt，Kui，Ks，KQon the dynamic characteristics of the system

圖7 由作動器活塞面積A 與力臂長度R 的乘積AR 對系統動態特性影響Fig.7 Effects of the product（AR）of the piston area of the actuator（A）and the length of the moment arm（R）on the dynamic characteristics of the system

圖6中Kt、Kui、Ks、KQ對系統動態特性影響的原因是：當有指令δc輸入，系統會產生壓差PL以及用來彌補壓差PL所引起的流量變化的偏差Δδ=δ?δc，而當Kt、Kui、Ks、KQ增大時，單位偏差可以產生更大的流量變化，則可以用更小的偏差Δδ來彌補壓差PL所造成的流量變化。因此Kt、Kui、Ks、KQ增加，系統所產生的偏差Δδ減小（見圖6（b））；穩態誤差減小（見圖6（c））；相同頻率下，閉環幅頻特性曲線所對應的對數幅頻值增大，閉環幅頻特性曲線衰減減慢，帶寬隨之增加（見圖6（a））。此外，當擺角到達最大值附近時，速度很小，接近于0，目標角與輸出角之差約等于穩態誤差，而隨著Kt、Kui、Ks、KQ的增加，穩態誤差減小，電液伺服機構-變剛度變阻尼模型遲滯曲線最大振幅及其力矩也隨之增加。圖7中AR對系統動態特性影響的原因同理。

由圖6 和圖7 還可以看出：作動器活塞面積A、力臂長度R對系統動態特性影響次于電液伺服機構反饋系數Kt、放大器靜態放大系數Kui、電液伺服機構一階表現系數Ks、滑閥流量增益KQ。

圖8為電液伺服閥頻率ωs對系統動態特性的影響。圖8（a）為不同ωs作用下的系統閉環幅頻特性曲線。由圖8（a）可以看出：隨著ωs的增加，帶寬基本不變。圖8（b）為不同ωs作用下的電液伺服機構-變剛度變阻尼模型遲滯曲線。由圖8（b）可以看出：ωs對遲滯曲線影響不大。圖8（c）為不同ωs作用下的電液伺服機構-變剛度變阻尼模型動態響應曲線。由圖8（c）可以看出：隨著ωs的增大，動態響應曲線的超調量略增加，響應速度、調節時間、穩態誤差的變化均不大。綜上所述，電液伺服閥頻率ωs遠大于系統帶寬頻率，對系統的動態特性基本無影響。

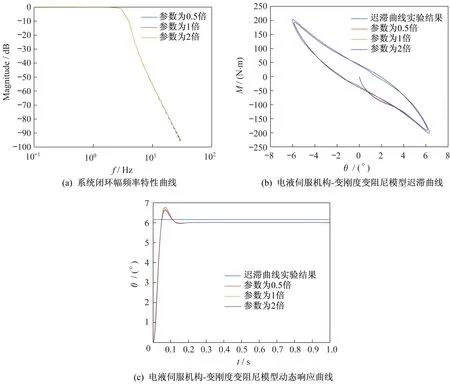
圖8 ωs對系統動態特性影響Fig.8 Effects of ωson the dynamic characteristics of the system

5 結束語

本文結合電液伺服機構和柔性接頭變剛度-變阻尼模型，構造了柔性噴管的電液伺服機構-變剛度變阻尼模型，分析了不同參數對電液伺服機構-變剛度變阻尼模型動態特性的影響，并和柔性噴管的電液伺服機構-定剛度定阻尼模型相比較。分析結果表明：與電液伺服機構-定剛度定阻尼模型相比，電液伺服機構-變剛度變阻尼模型所構造的遲滯曲線可以更準確地與遲滯實驗結果相吻合，預測實驗結果隨頻率變化的規律，并可以準確地模擬不同工作壓強、振幅條件下的柔性接頭遲滯曲線實驗結果；電液伺服機構反饋系數、放大器靜態放大系數、電液伺服機構增益、滑閥流量增益對系統動態特性的影響最為顯著，作動器活塞面積、力臂長度對系統動態特性影響次之，電液伺服閥一階表現頻率對系統動態特性影響最小。此外，值得注意的是，本文所構造的模型只能預測遲滯曲線實驗結果隨頻率的變化規律，無法對實驗結果隨振幅、壓強的變化規律進行預測，在之后的工作中將針對這一問題進行改進。