部分充填式鋼箱-混凝土連續組合梁剛度分析

莫時旭， 蔣越， 鄭艷， 韓濤

(1. 桂林理工大學 土木與建筑工程學院， 廣西 桂林 541004；2. 桂林理工大學 廣西建筑新能源與節能重點實驗室， 廣西 桂林 541004)

交通與橋梁的發展是我國經濟與科技發展的基礎，是我國綜合實力的體現因素之一[1].近幾十年來，隨著我國經濟的高速增長，鋼鐵工業飛速發展，鋼年產量近十億噸，為鋼結構和鋼混組合結構橋梁的發展打下了堅實的物質基礎.2015年5月，交通部發布了《對我國橋梁技術發展戰略的思考》的研究報告；2016年8月，交通部發布了《關于推進公路鋼結構橋梁建設的指導意見》，這類政策和報告的發布為鋼結構與組合結構的發展創造了新的發展機遇，有利于促進我國公路橋梁向資源節約、環境友好型發展[2-3].鋼箱混凝土組合梁因性能優良，在我國橋梁工程中得到廣泛應用，國內外學者也對其開展了大量的研究[4-11].美國結構設計規范在考慮界面滑移影響的基礎上，推導出和剪力連接程度有關的計算梁有效剛度的簡化公式[12].童根樹等[13]提出組合系數法，避免了鋼箱梁和混凝土板繞自身形心軸的抗彎剛度進行折減的問題.胡夏閩等[14]考慮了鋼箱混凝土組合梁界面的相對滑移，提出鋼混凝土組合梁撓度計算的附加曲率法.GBJ 17-88《鋼結構設計規范》[15]運用換算截面法計算組合梁截面的抗彎剛度，該方法步驟簡單，但沒有考慮兩種材料的滑移效應.現行規范GB 50017-2017《鋼結構設計規范》[16]采用聶建國提出的折減剛度法.由于混凝土和鋼梁的交接面的滑移導致附加曲率的產生，從而使截面的彈性抗彎承載力減小，聶建國則推導了滑移移效應引起的附加撓度計算公式.本文設計了3組不同抗剪連接度的試驗梁，將理論與試驗數據結合，對部分充填式窄幅鋼箱-混凝土連續組合梁進行剛度分析.

1 試驗概況

1.1 試件設計

設計3根充填式窄幅鋼箱-混凝土連續組合梁試件，編號分別為PFSCB1，PFSCB2，PFSCB3.試驗梁的長度為6.40 m,高度為0.42 m.鋼箱采用Q235鋼板，頂板與底板厚度均為10 mm，腹板厚度為4 mm.試驗梁立面和負彎矩區橫截面圖,如圖1所示.

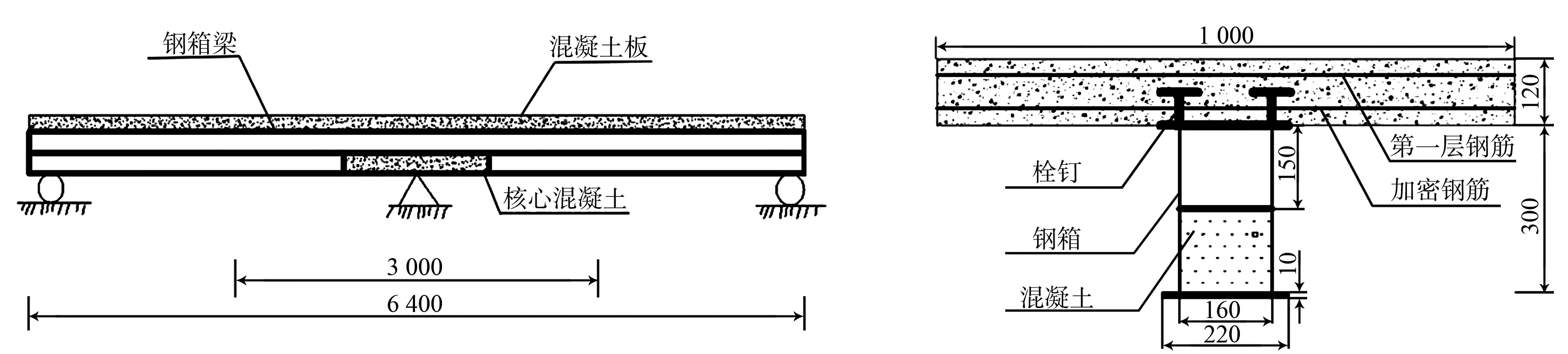
(a) 立面 (b) 負彎矩區橫截面圖1 試驗梁立面和負彎矩區橫截面圖(單位：mm)Fig.1 Elevation and section diagram of negative moment zone of test beam (unit: mm)

采用直徑為13 mm的4.8級普通栓連接混凝土面板與鋼箱，抗剪連接度通過栓釘間距設定.栓釘分區示意圖，如圖2所示.栓釘布置參數，如表1所示.表1中：n為栓釘數量；s為栓釘間距.

圖2 栓釘分區示意圖Fig.2 Schematic diagram of stud division

表1 栓釘布置參數
Tab.1 Arrangement parameters of studs

試件編號抗剪連接度M1區(左右兩側)n/個s/mmM2區(中間區域)n/個s/mmPFSCB11.00221503490PFSCB20.751621526120PFSCB30.501230018176

1.2 材料力學性能

按照標準金屬材料拉伸試驗方法，測試鋼材中鋼板和鋼筋的力學性能.栓釘的抗剪承載力采用ECCS標準推出試驗，通過計算得到單根栓釘抗剪承載力為72 kN.

鋼材的力學性能，如表2所示.表2中：φ，d分別為鋼筋直徑和鋼板厚度；fy為屈服強度；ft為抗拉強度；E為彈性模量.

28 d時和試驗時,實測的混凝土力學性能，如表3所示.表3中：fcu,W，fcu,B分別表示混凝土翼板立方體抗壓強度和混凝土箱內立方體抗壓強度.

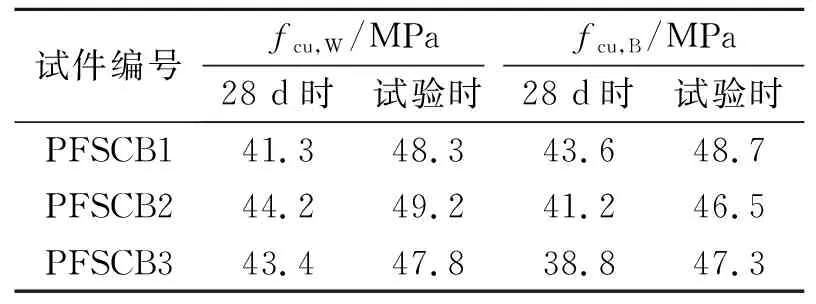
表3 混凝土力學性能Tab.3 Mechanical properties of concrete

表2 鋼材的力學性能Tab.2 Mechanical properties of steel

圖3 加載裝置Fig.3 Loading device

1.3 試驗裝置及加載方案

采用靜力加載的方式，加載裝置，如圖3所示.將千斤頂放置在兩跨連續實驗梁跨中的位置，在試件梁的跨中、中支座截面處相應的位置布置電阻應變片，兩端支座及加載點處放置壓力傳感器.

試驗梁硂面板及鋼箱應變片布置，如圖4所示.在組合梁的支座，L/4，L/2，3L/4(L為試驗梁的總長度)截面混凝土翼板與鋼箱界面處安置數顯式千分表，用于測量翼板、支座的位移和鋼箱相對滑移.在試驗過程中，使用裂縫放大器測量裂縫寬度，并觀察裂縫發展情況.

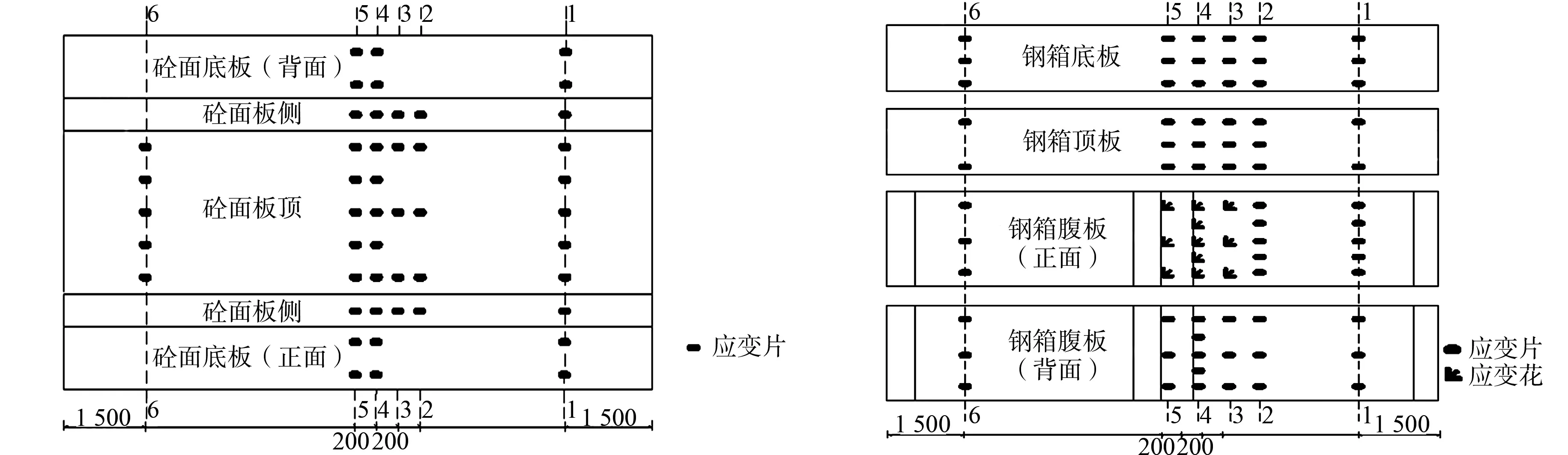
(a) 砼面板應變片 (b) 鋼箱應變片圖4 硂面板與鋼箱應變片布置圖(單位：mm)Fig.4 Layout of concrete panel and steel box strain gauge (unit: mm)

2 試驗現象及破壞模式

2.1 試驗現象

各梁的實驗現象大致相同，現以試驗梁PFSCB3為例，介紹梁的實驗過程及現象.當加載到120 kN左右時，混凝土翼板中支座處出現了第一條可見裂縫，隨著荷載增加，裂縫寬度增加，同時生成其他裂縫;當加載到240 kN左右時，中支座處的混凝土翼板出現第一條貫通裂縫;當加載到360 kN左右時，聽到“砰”的聲響，表明鋼箱與混凝土翼板交界面處自然粘結破壞;當加載到400～600 kN時，出現“咔”的聲響，混凝土下翼緣出現較大裂縫；當加載超過600 kN時，梁的鋼箱腹板發生屈曲；當加載達到800 kN時，到達極限承載階段，此時，混凝土翼板出現大量貫通裂縫.

2.2 破壞模式

每根梁的破壞模式各有差異.試驗梁PFSCB1的破壞形態，如圖5(a)所示.由圖5(a)可知：因為梁跨中截面區鋼箱底板的焊接裂縫拉裂而造成突然破壞，此時，梁的鋼箱腹板未完全屈曲且梁的混凝土翼板未完全壓碎；剝開鋼箱，核心混凝土下部有多條裂縫，但都未完全貫通.試驗梁PFSCB2的破壞形態，如圖5(b)所示.由圖5(b)可知：跨中截面混凝土翼板底面出現較多貫通裂縫，說明在梁跨中截面的中心軸已經向上移至混凝土翼板;試驗梁鋼箱跨中正彎矩區至反彎點附近產生近似斜向45°外鼓屈曲波，由于正彎矩區段為空鋼箱梁，屈曲波發展范圍較大，但受到鋼箱頂底板約束作用較強，頂底板沒有出現屈曲;剝開鋼箱，發現核心混凝土沿剪切面斷裂，是典型的剪切破壞.試驗梁PFSCB3的破壞形態,如圖5(c),(d)所示.由圖5(c),(d)可知：混凝土翼板頂面的裂縫開展較少，梁的跨中截面鋼箱腹板出現一條45°斜向屈曲內凹，從負彎矩區填充混凝土段上箱室延伸至正彎矩區未填充混凝土下箱室；負彎矩區段填充混凝土后抑制了腹板的內屈，下箱室腹板屈曲不明顯；剝開鋼箱，發現核心混凝土棱柱體依舊保持著整體性，說明鋼箱的約束充分發揮了作用;內部填充的核心混凝土產生剪切斜裂縫，組合梁承載能力沒有明顯下降，表現出良好的延性.

(a) PFSCB1 (b) PFSCB2

(c) PFSCB3表面圖 (d) PFSCB3內部圖圖5 試驗梁的破壞形態Fig.5 Failure mode of test beam

3 實驗結果與分析

3.1 荷載-撓度曲線

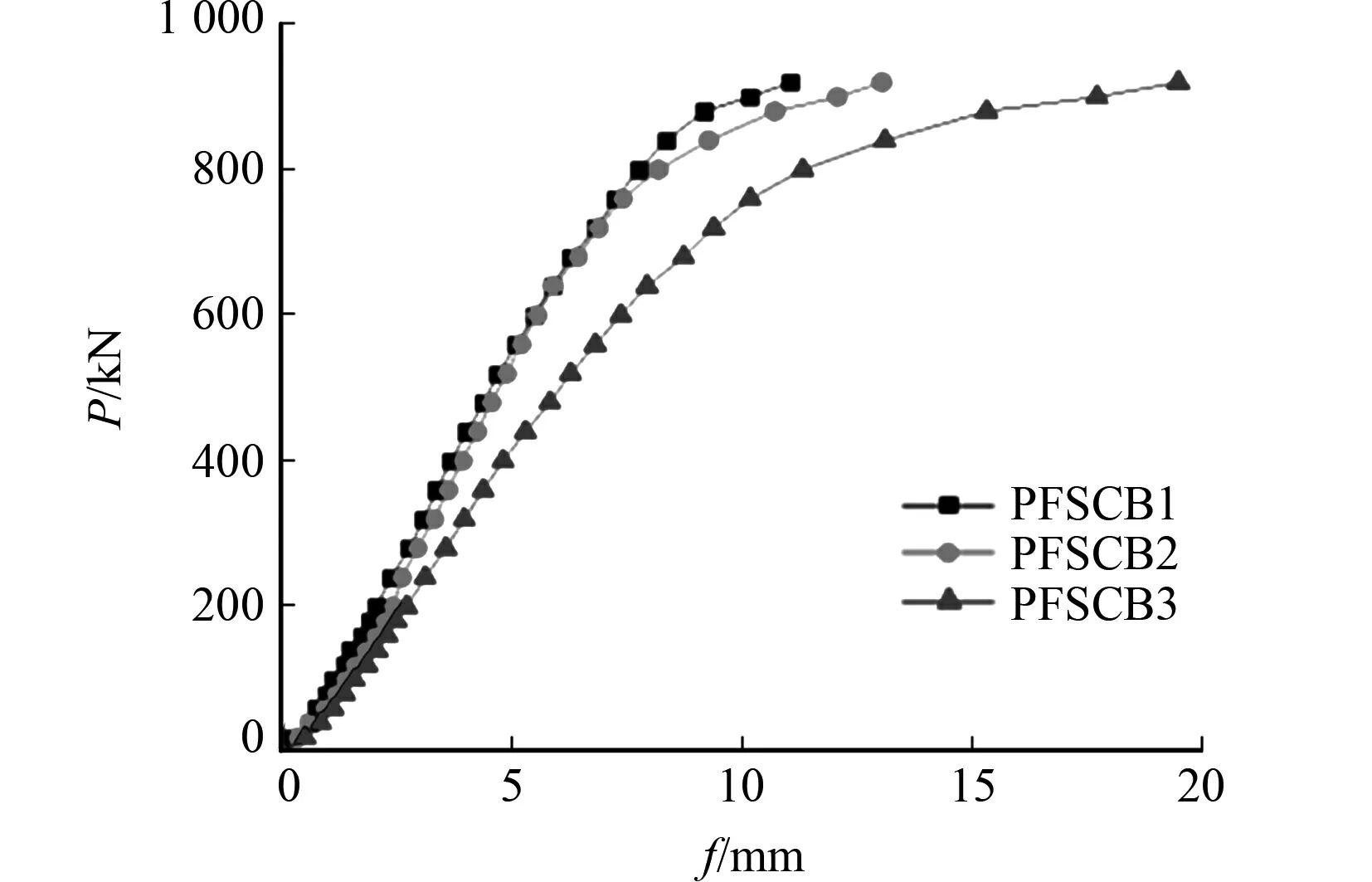
圖6 試驗梁的跨中荷載-撓度曲線Fig.6 Load-deflection curve of test beam

撓度值可直接反映組合梁在各階段的受力性能.試驗梁的跨中荷載(P)-撓度(f)曲線,如圖6所示.由圖6可知：在開始加載時，試驗梁處于彈性工作階段，充分發揮了組合梁的組合效應，3組試驗梁的撓度隨荷載的變化趨勢比較相近，曲線都呈線性變化，撓度緩慢增加，說明試驗梁在彈性工作階段的抗剪連接度對撓度值的影響較小；當加載至彈塑性工作階段時，曲線的曲率開始逐漸增大，組合梁撓度隨荷載增加變化明顯，該階段抗剪連接度較大的試驗梁PFSCB1的撓度值增長最為緩慢；當繼續加載至塑性階段時，荷載-撓度曲線慢慢變平，此時，鋼箱梁的變形速度明顯快于荷載的增加速率；在所受荷載相同的情況下，抗剪連接度最大的試驗梁PFSCB1的撓度值最小.

3.2 鋼箱底板的荷載-應變曲線

鋼箱底板中支座的荷載-應變(ε)曲線，如圖7(a)所示.由圖7(a)可知：在加載初期，3組試驗梁鋼箱梁底板的荷載-應變曲線較為接近，基本呈線性變化；當進入塑性階段，試驗梁充分發揮材料的強度；試驗梁PFSCB1應變急劇增加，說明中支座負彎矩區底板受拉而出現局部屈曲，組合梁的整體剛度變小、變形增大；試驗梁PFSCB2，PFSCB3應變增大也較為明顯，但是應變曲線與PFSCB1相比較為緩和；在塑性破壞階段，隨著荷載增加，應變增加的速度變快，直至鋼箱破壞，應變值不再隨荷載增加.

鋼箱底板跨中的荷載-應變曲線，如圖7(b)所示.由圖7(b)可知：在受力開始時，曲線呈線性變化，混凝土翼板與鋼箱梁組合效應良好；隨著荷載的增加，由于連續組合梁跨中位置為空鋼箱，沒有核心混凝土與鋼箱梁一起承擔荷載，所以組合梁跨中截面變形較大；當荷載加至0.8 Pa時，鋼箱梁底板荷載應變曲線出現了小小的突變，局部屈曲速率加快，使應變急劇的增加；在塑性破壞階段，荷載-應變曲線較為緩和是因為形成了塑性鉸，使連續組合梁發生彎矩重分布.

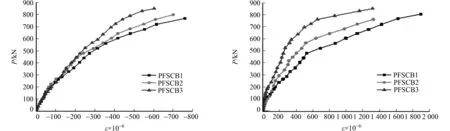
(a) 中支座 (b) 跨中圖7 鋼箱底板中支座和跨中的荷載-應變曲線Fig.7 Load-strain curve of steel box middle support and midspan of steel box bottom slab

3.3 截面高度-應變分布

沿梁高方向，在連續組合梁中支座截面和跨中截面粘貼1豎排5片間距為50 mm的應變片，用于測量鋼箱腹板在荷載作用下的應變.試驗梁PFSCB1中支座截面和跨中截面的應變分布,如圖8所示.圖8中：h為鋼箱截面高度.由圖8(a)可知：在荷載達到80%的極限荷載以前，試驗梁處于彈性階段，應變值沿梁高呈線性關系，滿足平截面假定；隨著荷載的增加，鋼箱梁出現局部屈曲，導致試驗梁的剛度不斷減小，鋼箱應變值增大明顯;當試驗梁處于彈塑性工作階段時，鋼箱梁跨中位置局部屈曲加劇，中支座附近塑性鉸慢慢形成，使中性軸略有上升.由此可知,試驗梁的組合效應增加了梁體的延性和剛度.

由圖8(b)可知：試驗梁跨中部位為正彎矩區，在翼板受壓而鋼梁受拉時，鋼梁內無核心混凝土共同承擔受力，因此，試驗梁翼板在整個受力過程中承擔較大的承載力.在彈性工作階段，跨中部位腹板應變隨梁高呈線性變化，基本符合平截面假定.在彈塑性工作階段，鋼梁腹板應變出現突變，試驗梁跨中截面鋼箱受到較大的壓應力而發生局部屈曲，屈曲呈現正弦波狀起伏的屈曲形態，而翼板還具有較好的抗壓承載能力，中和軸開始慢慢上移.與中支座區相比，跨中區鋼梁產生的局部屈曲行為更為明顯，中性軸更靠近鋼箱頂板.

(a) 中支座截面 (b) 跨中截面圖8 試驗梁PFSCB1中支座截面和跨中截面的應變分布Fig.8 Strain distribution of middle support section and mid-span section of PFSCB1 test beam

4 剛度分析

連續組合梁中支座區鋼箱下翼緣充填部分混凝土.假設鋼箱和混凝土均為理想彈性體，符合平截面假定.采用換算截面法計算鋼箱的截面特性，即把混凝土截面換算成等效的鋼截面.

1) 中和軸位于核心混凝土處(x?hc).

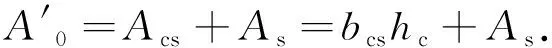
(1)

組合截面中和軸至鋼箱底板的距離x為

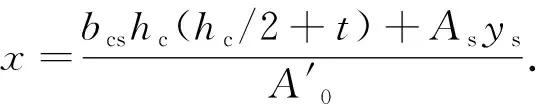
(2)

組合截面的慣性矩Is為

(3)

2) 中和軸位于非核心混凝土處(x>hc).

組合截面面積為

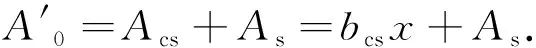
(4)

組合截面中和軸至鋼箱底板的距離為

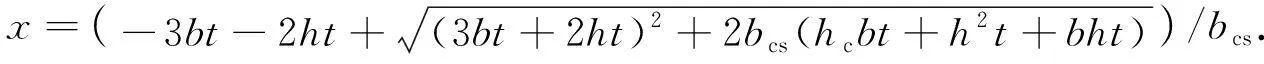
(5)

組合截面的慣性矩為

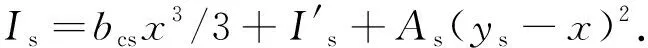
(6)

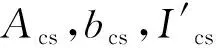
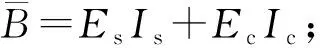
考慮邊界條件對剛度的影響,王立憲等[17]提出折減剛度系數ζ,其表達式為

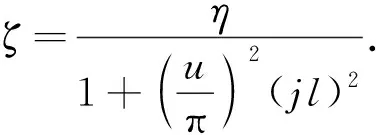
(7)

式(7)中：u為計算長度因子，此處取值為0.5；其他參數及推導見文獻[17].

為了簡化式子，引入常數v，w，則有

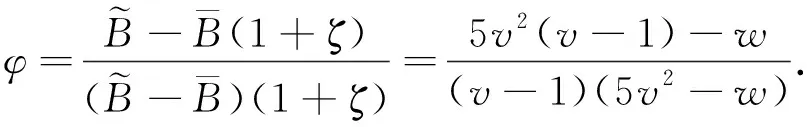
(8)

將鋼箱-混凝土組合梁和空鋼箱梁跨中的撓度計算值與實測值進行比較，如表4所示.表4中：f為鋼箱-混凝土組合梁撓度的實測值；f′為鋼箱-混凝土梁撓度的計算值；f″為空鋼箱梁撓度的計算值.

表4 撓度計算值與實測值的對比Tab.4 Comparison of calculated and measured deflection values

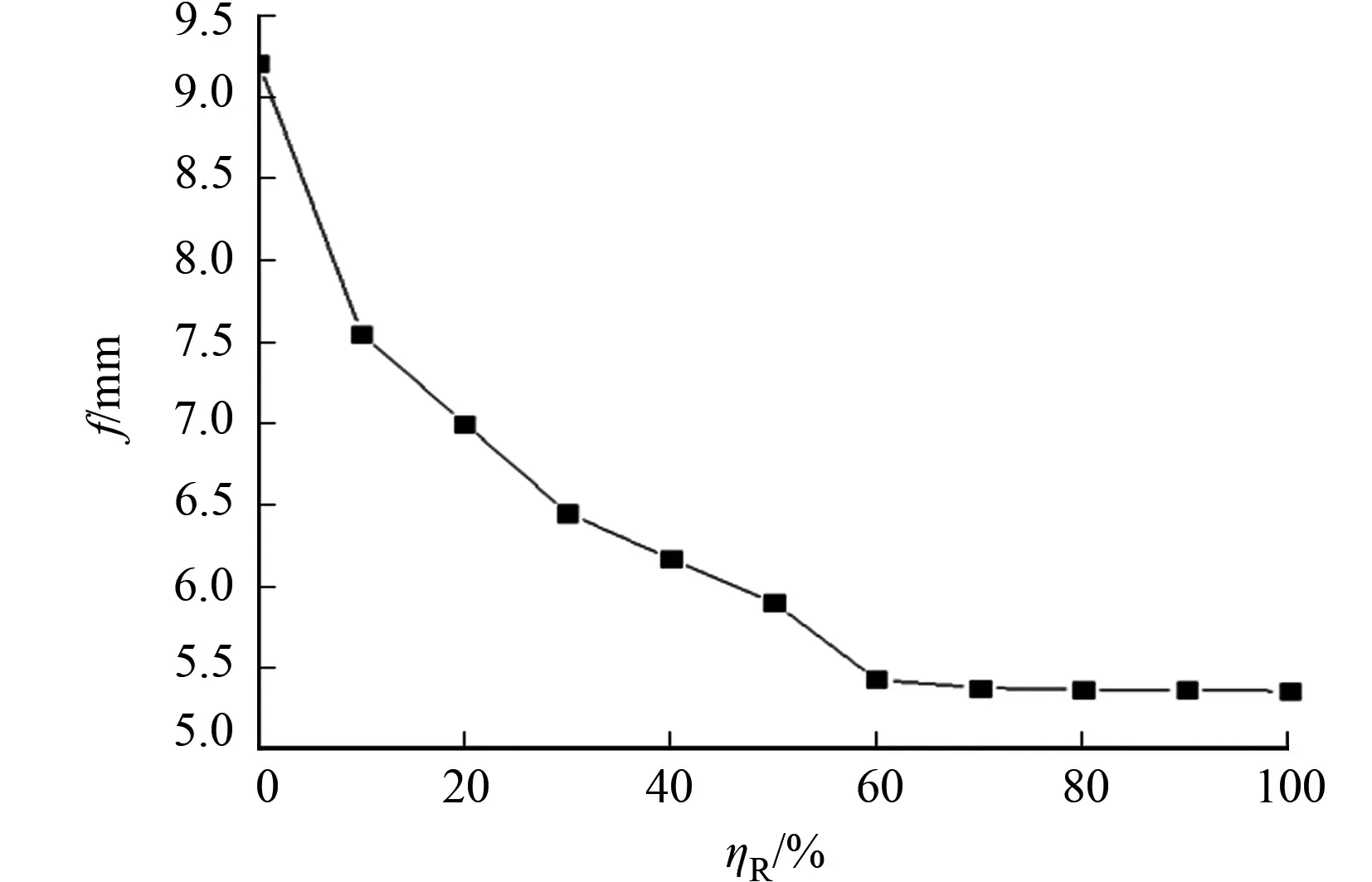
圖9 箱內充填混凝土量與跨中撓度計算值的關系Fig.9 Relationship between amount of concrete filled in box and calculation mid-span deflection

由表4可知：組合梁的抗剪連接度越大，其撓度值越小；鋼箱-混凝土組合梁的計算值大于實測值，且計算精度在合理范圍內；在所受荷載相同的情況下，與空鋼箱梁相比，鋼箱-混凝土組合梁的撓度值減小20%左右，說明鋼箱內部分充填混凝土對撓度有很大的影響，鋼箱-混凝土組合梁比空鋼箱梁有更高的承載能力和更好的延性.

在組合梁抗剪連接度為1.00的情況下，計算由空鋼箱(混凝土充填量ηR=0%)到全充填(ηR=100%)時組合梁的撓度.箱內充填混凝土量與跨中撓度計算值的關系，如圖9所示.由圖9可知：從空鋼箱至ηR為10%時,撓度下降最快;當ηR為10%～60%時，撓度下降稍微緩慢；當ηR為60%時，發生突變直至全填充，撓度基本保持不變.由此可知，隨著組合梁箱內混凝土充填量的增加，箱內受壓區逐漸提高，當ηR達到60%后，箱內受壓區保持不變，使部分充填混凝土受拉.

5 結論

對3根部分充填式窄幅鋼箱混凝土連續組合梁進行反向加載試驗，分析組合梁的變形情況，并對剛度計算方法進行研究，得到以下3點結論.

1) 鋼箱混凝土組合梁的撓度與抗剪連接度有關.在彈性階段，組合梁的抗剪連接度越大，撓度越小，當抗剪連接度達到0.75后，撓度變化較小.

2) 在組合梁鋼箱內充填混凝土限制了鋼梁在受力時發生內屈，不僅提高了鋼箱混凝土連續組合的承載能力，還增加了梁體的剛度和延性.計算結果表明，組合梁鋼箱內充填混凝土比空鋼箱的撓度值減小了20%左右.

3) 當組合梁抗剪連接度為1.00，鋼箱內混凝土充填量從0%增加至60%時，撓度值隨著充填量的增大而減小；當充填量達到60%以后，撓度值基本不變.因此，鋼箱內混凝土充填量為60%時，組合梁的剛度提高最明顯.