Β2上α次殆星映射的一類有界構造

王潔， 林珍連， 王建飛

(華僑大學 數學科學學院， 福建 泉州 362021)

1 預備知識

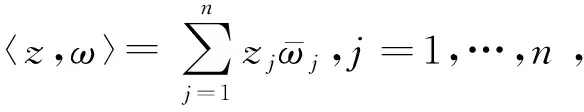
在單復變幾何函數論中，正實部函數是極為重要的函數族，記為P[1]，則有

將P推廣到多復變的單位球Βn上，記為M，則有

M={f∈H(Βn，Cn):f(0)=0，Re〈f(z)，z〉>0}.

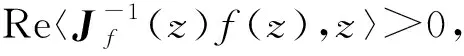
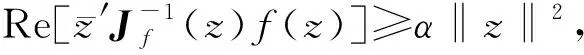
注1當α=0，定義2即為單位球Βn上的星形映射[7-8].

文獻[9]利用Ω的Minkowski泛函ρ(z)給出另一種星形映射及α次殆星映射的定義.由以上定義可知，若f是Ω上的α次殆星映射，則f必是Ω上的星形映射.

定義3[10-11]設{f(z，t)}t≥0，z∈Βn為一個全純映射族，f(0，t)=0，Jf(0，t)=exp(t)In.如果對于任意0≤s≤t<+∞都有f(·，s)f(·，t)，即存在全純映射v=v(·，s，t)，且v∈H(Βn，Cn)，使得‖v‖<1，v(0，s，t)=0，f(z，s)=f(v(z，s，t)，t)，0≤s≤t<+∞，z∈Βn.如果f(·，t)為Βn上的雙全純映射，則稱從屬鏈{f(z，t)}t≥0為L?ewner鏈.

星形映射及其子族是多復變數幾何函數論的主要研究對象之一，如何構造這些映射的例子十分重要[12-13].文中給出Β2上α次殆星映射的有界構造，應用這類有界映射，可得到α次殆星映射與L?ewner鏈的關系，文中結果推廣了Β2上星形映射的結果.

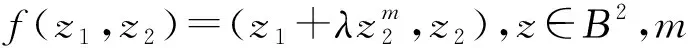
2 兩個引理

為證明以上主要結論，需引入以下2個引理.

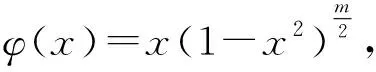
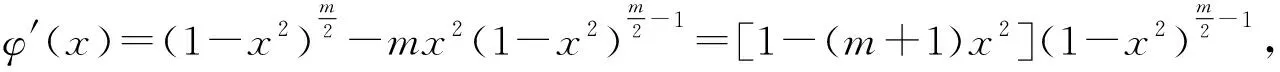
引理2[14]設映射族f(z，t)=exp(t)z+…:Βn×[0，+∞)→Cn滿足以下條件：1) 對任意的t≥0，f(·，t)∈H(Βn，Cn)；2) 對任意的z∈Βn，f(z，·)在[0，+∞)上絕對連續.

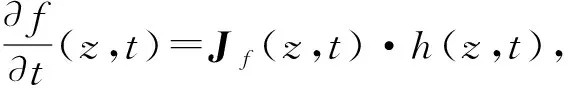
3 主要結果

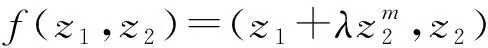
證明：顯然f(z1，z2)是Β2上的正規化雙全純映射，且f在C2上全純，由定義1可知，要證明f為Β2上的α次殆星映射，只需證明

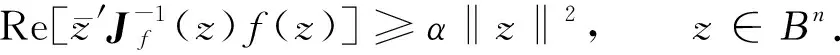
(1)

由調和函數的最小模原理可知，只需證明式(1)對z∈?Βn成立，則有

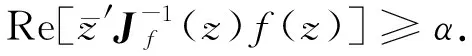
(2)

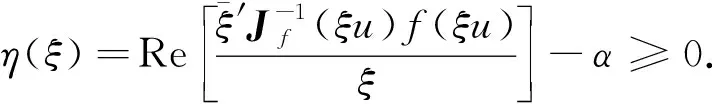
由式(2)可知，f為Β2上的α次殆星映射，當且僅當

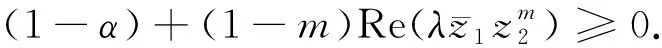
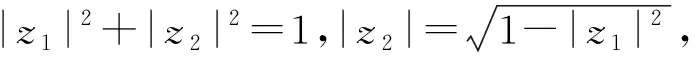
從而f為Β2上的α次殆星映射，當且僅當

由引理1可得

當α=0時，可得到推論1.

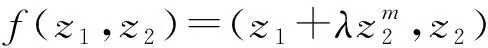
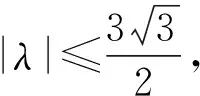
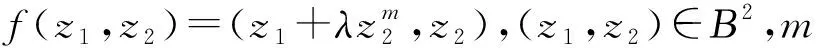
證明：由定理1可知，命題1)?命題2)，因此，只需證明命題2)?命題3).易見， 對于任何的t≥0，g(·，t)∈H(Β2，C2)，g(0，t)=0，Jg(0，t)=exp(t)I2，g(z，t)∈C∞(Β2×[0，+∞))，且有

注意到

從而有

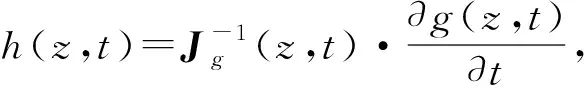
因此，g(z，t)是Β2上的L?ewner鏈，當且僅當Re〈h(z，t)，z〉>0，z∈Β2，t≥0，從而有

由類似定理1的方法可得

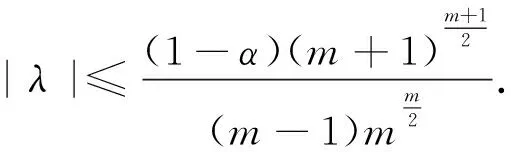
注3當α=0時，此結果由文獻[15]的引理2.3給出.