基于PSO-SVM的來水量預測模型

王龍強

（河北省水利水電第二勘測設計研究院，石家莊 050021）

降水、氣溫、徑流等多種因子具有很大的不確定性，并影響著中長期的水文預報情況。來水量在年際間具有較大的隨機性和不確定性，在影響來水量的眾多因素之間也存在著復雜關系，眾多因素之間的相互作用關系很難利用常規方法進行比較準確的表達。本文通過來水量模型的建立，利用某河45年的徑流資料對來年來水量進行預測，并與實際值進行比較。

1 來水量SVM模型

來水量預測模型是反應影響來水量的因素與來水量之間的關系。本文采用用于非線性建模與預測的支持向量回歸機模型。

以來水量預測模型為例，模型訓練輸入為影響因素。由影響因素對應的來水量得到一組輸入信號：來水量數據集（X，Y），即：

式中 xi∈Rn為輸入向量；yi∈Rn為與xi相對應的輸出向量；N為數據點總數。

通過輸入向量與輸出向量的點集進行函數回歸［1］，如式（2）：

式中 y為輸出向量；x為輸入向量；w，b為函數常數項。

假設在ε精度，所有訓練樣本可用線性擬合函數表示，如式（3）：

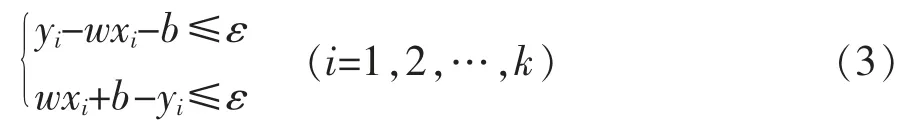
式中 ε 為精度；其他字母含義同上。

優化目標是最小化‖w‖2/2。由于允許誤差，引入松弛變量ξ≥0和≥0，如式（4）：

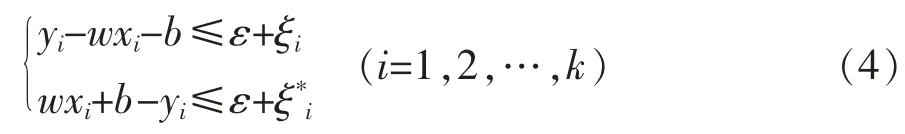
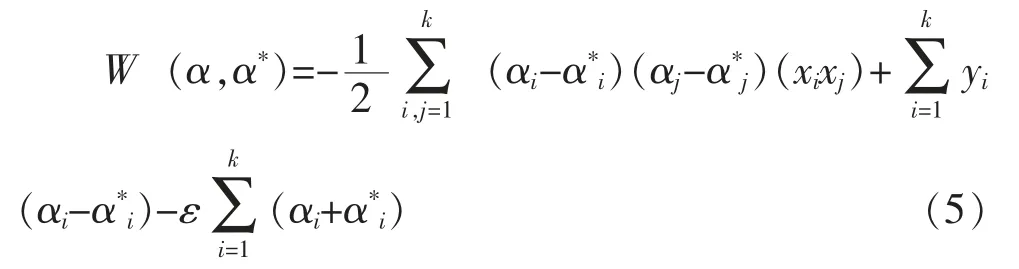
W（α，α*）最大時，由此得到支持向量機的擬合函數［2］f（x），如式（6）：

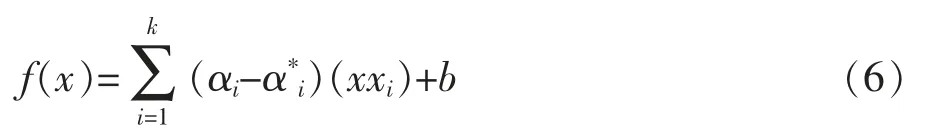
式中 W（α，α*）為目標函數；C為大于零的常數；αi，為Lagrange乘子，αi，將只有小部分不為0，對應的樣本即為支持向量；其他字母含義同上。

考慮到非線性問題可通過變換將問題映射到某個高維的特征空間進行求解。用核函數可代替線性問題的內積運算，即K（xi，xj）=φ（xi）φ（xj）。由此，式（5）變換如式（7）：

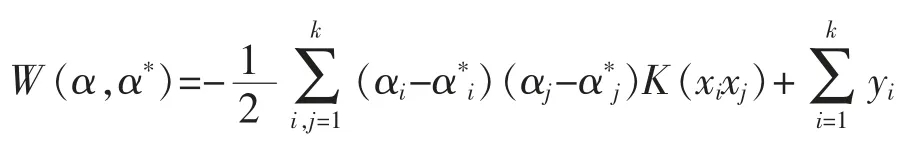
式中 字母含義同上。

那么式（6）擬合函數可變換如式（8）：

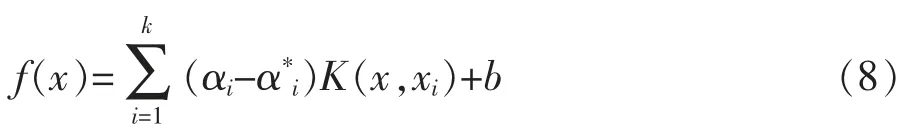
式中 K（x，xi）為核函數；其他字母含義同上。

本文所用為徑向基型，如式（9）：

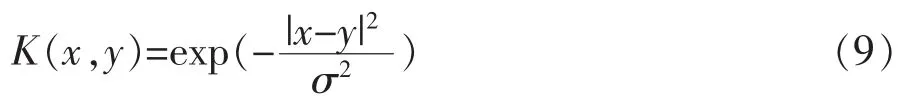
式中 σ 為核函數的寬度；其他字母含義同上。

以上為來水量預測的LS-SVM模型。

2 基于PSO的來水量模型SVM參數優化

粒子群優化算法PSO，是在人類對鳥類捕食時行為研究的基礎上得到的一種進化計算方法。由于粒子群算法容易實現且不需要調整過多參數因而被廣泛應用于多種領域。

采用某河流45年徑流資料對模型進行實例驗證，根據水庫前期徑流資料預測未來年份的來水量。

模型數據從資料的樣本集中選取45個數據，其中25個數據作為訓練樣本，10個數據作為校驗樣本數據，剩余10個數據作為測試樣本數據。設粒子群規模為45，SVM參數C的取值范圍 ［0.1，104］，σ 的取值范圍［10-3，10］，設最大迭代次數Gmax為500，加速因子c1為0.01，c2為0.01。目標函數為訓練樣本集和校驗樣本集的均方差之和為最小，經過PSO優化選擇得到使得目標函數最小的最優解C為2816，σ 為1.27。適應度值的迭代優化過程如圖1。

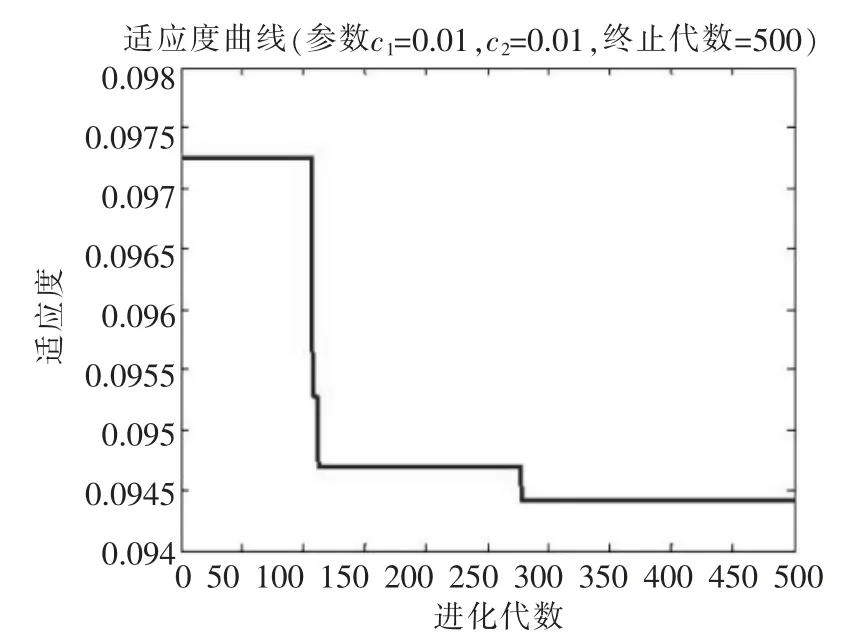
圖1 適應度函數進化過程

由圖1可見，在100代左右快速收斂，275代左右達到最優值。在最優參數的基礎上，模型對10個測試樣本數據進行測試，所得預測模型如圖2。

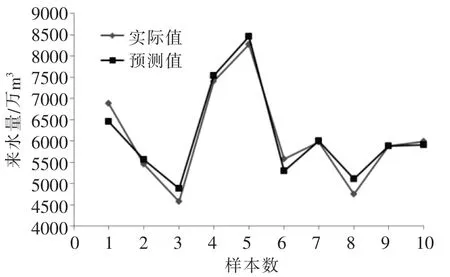
圖2 PSO-SVM預測模型

將模型所得預測值與實際值進行比較，所得誤差結果如表1。

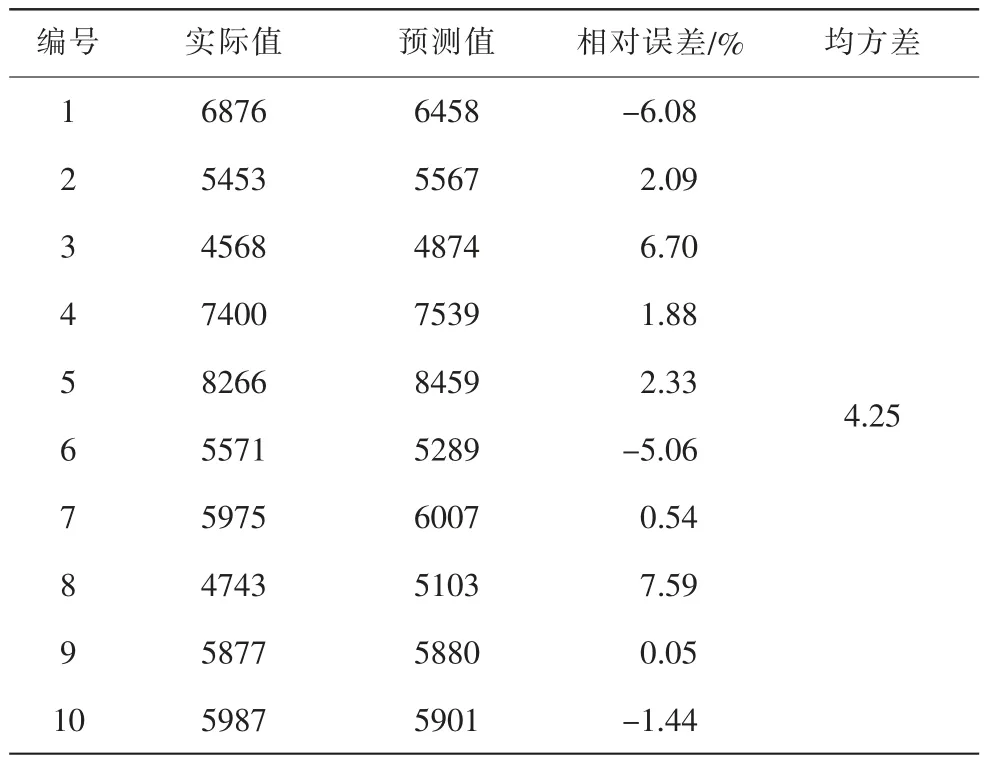
表1 PSO-SVM預測結果

實際值與預測值的相對誤差絕對值最大值7.59，最小值0.05，均方差4.25。

3 模型比較

本文用相同數據建立BP神經網絡模型與PSOSVM模型數據進行比較，BP神經網絡預測模型［3］如圖3，預測值與實際值的比較如表2。

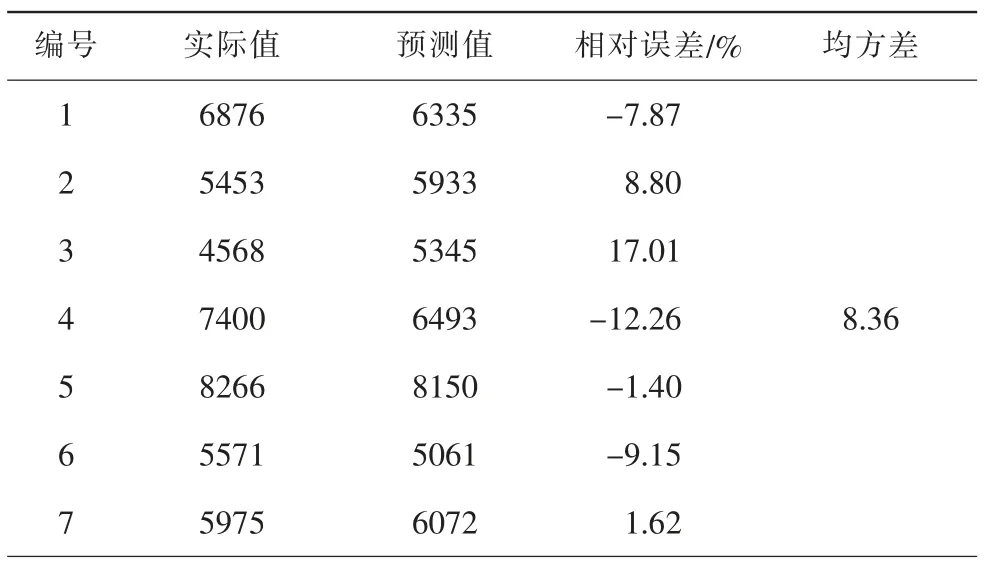
表2 BP神經網絡預測結果

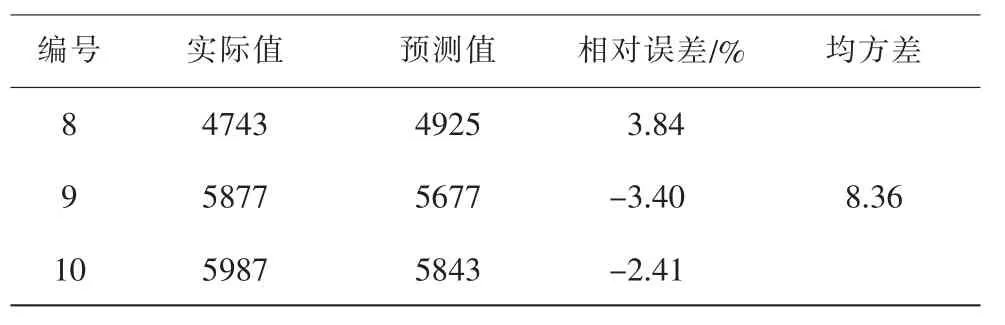
續表2

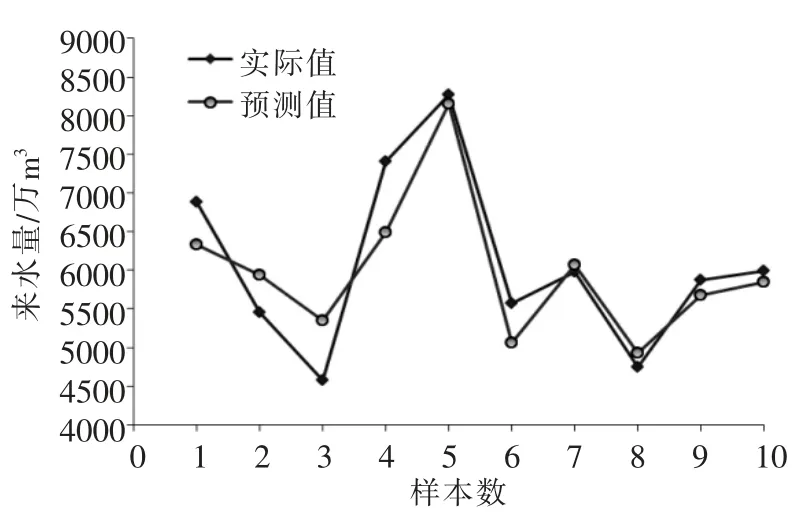
圖3 BP神經網絡預測模型

BP神經網絡模型所得預測值與實際值相對誤差的絕對值最大17.01%，最小1.40%，均方差8.36。

從兩種模型的預測曲線擬合程度來看，PSOSVM模型擬合程度明顯好于BP神經網絡模型；從表中的數據分析結果來看，PSO-SVM模型的預測值與實際值的誤差的均方差小于BP神經網絡預測模型值；PSO-SVM模型對來水量的預測精度更高。

4 結語

建立了來水量PSO-SVM模型，并利用樣本數據進行了訓練與預測，并利用BP神經網絡模型對同一組數據進行了預測，模型數據結果分析表明：PSOSVM模型預測值與實際值的均方差小于BP神經網絡，PSO-SVM對預測曲線的擬合程度高于BP神經網絡。PSO-SVM模型能夠為來水量的預測提供更為精準的參考依據。