基于Hansbo滲流法的砂井地基固結處理分析

張永強

（鼎晟工程試驗檢測有限公司，新疆 和田848000）

在進行砂井地基固結處理的過程中，基于Darcy定律的砂井固結法往往是最為有效的方法。但是，這種砂井地基固結分析方法是基于理想狀況下的砂井建立的滲流方程，在實際應用中，受到土質狀況、砂井深度等的影響，Darcy定律很難完全適用。于是，Hansbo等人提出了Barron理論，該理論充分考慮了在有不變應變影響時砂井地基凝固的影響因素，如井阻作用、涂抹效應等。為進一步研究Hansbo滲流法的砂井地基固結算法和模型，對地基固結方程進行了重新推導驗證，并在Barron的假設條件下，對砂井地基固結進行相關參數的探究［1］。

1 建立基于Hansbo滲流法地基固化模型

Hansbo滲流法的礦井地基固化模型的建立過程包括：首先對模型進行參數設定，然后提出基本假設條件，最后建立分析模型。

1.1 模型參數設定

對Hansbo滲流法砂井地基模型進行參數設定，首先應假設某均質飽和黏土層的厚度為H，已經在自身重力作用下完全固結。同時，假設該飽和黏土層的頂面透水，底面不透水，砂井形成后對頂面施加豎向均勻分布的載荷為q。砂井的半徑為rw，影響區半徑為re。此時，若忽略井阻作用和涂抹效應的影響，模型參數設定，如圖1。

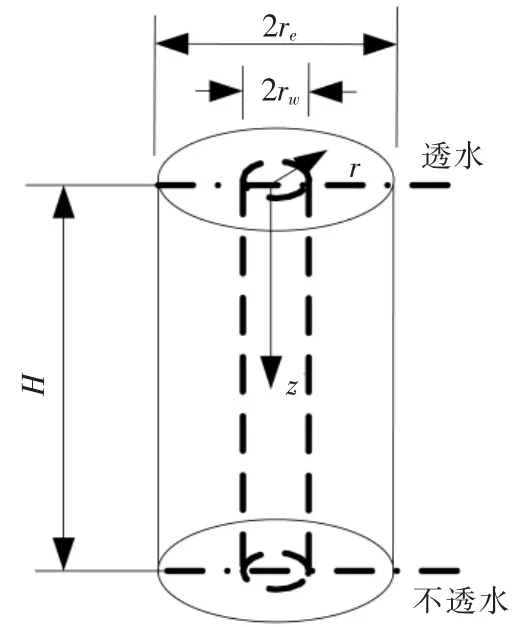
圖1 砂井模型參數設定

1.2 模型假設條件

Hansbo滲流法砂井地基模型需要遵循基本的假設條件［2］，才能對砂井地基固結問題進行簡化和計算。應滿足的假設條件有：

（1）飽和黏土層的頂面施加的豎向均勻分布載荷大小為q，在初始階段的固結階段，載荷q全部被黏土層中超孔隙水壓u負載。

（2）在黏土層固結中期階段，豎向載荷引起的豎向應變可以自由變化，且均布載荷不會因固結過程而改變載荷的分布情況。

（3）對黏土層進行施壓后僅沿壓力方向進行豎向變形，其他方向的變形忽略不計。

（4）黏土層的滲流方向可沿各個方向進行，即同時考慮橫向滲流和豎向滲流。在滲流過程中，要假定基于Hansbo滲流模型的滲流參數保持不變。

（5）若需要計算涂抹效應的影響，需要假定涂抹范圍內的滲透參數恒定不變。

1.3 模型建立

設模型經過t時刻后，在距離黏土層頂部距離為z處，距離砂井模型中心軸r處的超孔壓為u，體積應變為εv，水力梯度為i。根據之前假設的條件——滲流的連續性，可得在軸對稱情況下的滲流連續性方程［3］如式（1）：

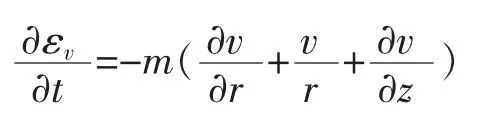
式中 m為黏土層的質量；v為黏土層的泊松比；r為黏土層距離沙井軸心處的距離；εv為黏土層的體積應變。

對超孔隙水的豎向和徑向滲流速度進行公式化規范如式（2）：

式中 滲流速度v恒定為正值；iz和ir分別為恒定位正值的豎向孔隙水深流速度和橫向孔隙水的滲流速度［4］。

將式（1），式（2）進行整理代入，最終可得各方向滲流速度均勻的條件下的固結方程，如式（3）：

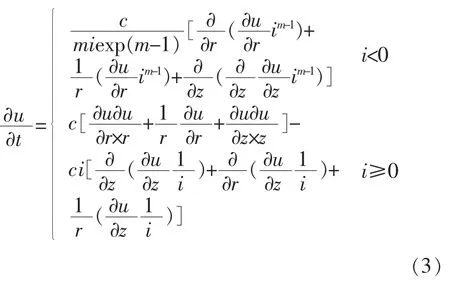
式中 C為滲流參數，是與泊松比成反比的恒定值；u為超孔隙水壓；其他參數均不發生變化。

2 基于Hansbo滲流法地基固化模型求解

基于Hansbo滲流法地基固化模型經過參數設定，條件假設到建立數字化模型后，對模型的公式進行求解和驗算。采用了最為精確、簡便的方法——有限元差分法［5］進行求解。

2.1 砂井地基固化模型求解

采用有限元差分法進行求解。FlexPDF軟件是一款專用于求解有限元偏分方程和微分方程的軟件。通常，可以在較短時間內精確求解三維及三維以下方程的漸變過程、發展趨勢及特征值問題等。

需注意在采用該軟件進行求解時，要在之前假設模型建立的參數設定和假設條件下進行。同時，也要保證黏土層的滲流的連續性和各方向均質性等特點，這樣才能保證軟件計算的準確性［6］。

2.2 砂井地基固化模型的驗算

在當前已有的研究基礎上，選取特殊的參數值進行帶入驗算。當m=1，i=0，t=0.5的理想情況下，討論基于Hansbo滲流在均勻應力條件下的砂井地基固化模型。經過軟件計算，可得到相關的理想狀態下砂井地基固化模型的理想參數值。最后，將本模型公式計算的理想參數值與當前研究的理論值進行參比對照，以確定建立的砂井地基固化模型公式計算結果是否準確，如表1。

表1 理想砂井地基固化模型參數值

從表1結果可以看出，本文建立的基于Hansbo滲流法的砂井地基固化模型與當前研究的理論值大幅度吻合，說明該模型計算過程無較大誤差，計算結果真實可靠，說明模型可靠，能夠應用于下一步的實例研究中。

3 影響因素實驗分析

為了對基于Hansbo滲流法砂井地基固化模型準確性進一步探究，需要對模型的影響參數進行探究，盡可能排除誤差。

3.1 對超孔隙壓力的影響

通過研究在模型計算值與理論值時超孔隙壓力（分為徑向壓力和豎向壓力） 對滲流參數的影響曲線，基于Hansbo滲流法的砂井地基固化模型比傳統Hansbo滲流模型的超孔隙壓力要大。且當其他滲流參數越大，如時間影響因子越大，兩種模型的超孔隙壓力差異性就越大。

通過分析發現，對于同一時刻，在同一位置處的參考點，超孔隙孔壓隨離開黏土層頂面的距離增大而增大，但在超過某一極限值后，超孔隙孔壓幾乎不再發生變化，變為一個恒定值。也就是說，在砂井地基固化凝固層的固化過程中，由于豎向的排水路徑較徑向排水路徑長，所以徑向排水導致的超孔隙孔壓減弱才是主要原因。

分析傳統Hansbo 滲流法建立的模型和基于Hansbo滲流法的砂井地基固化模型對超空隙孔壓的影響對比如圖2。

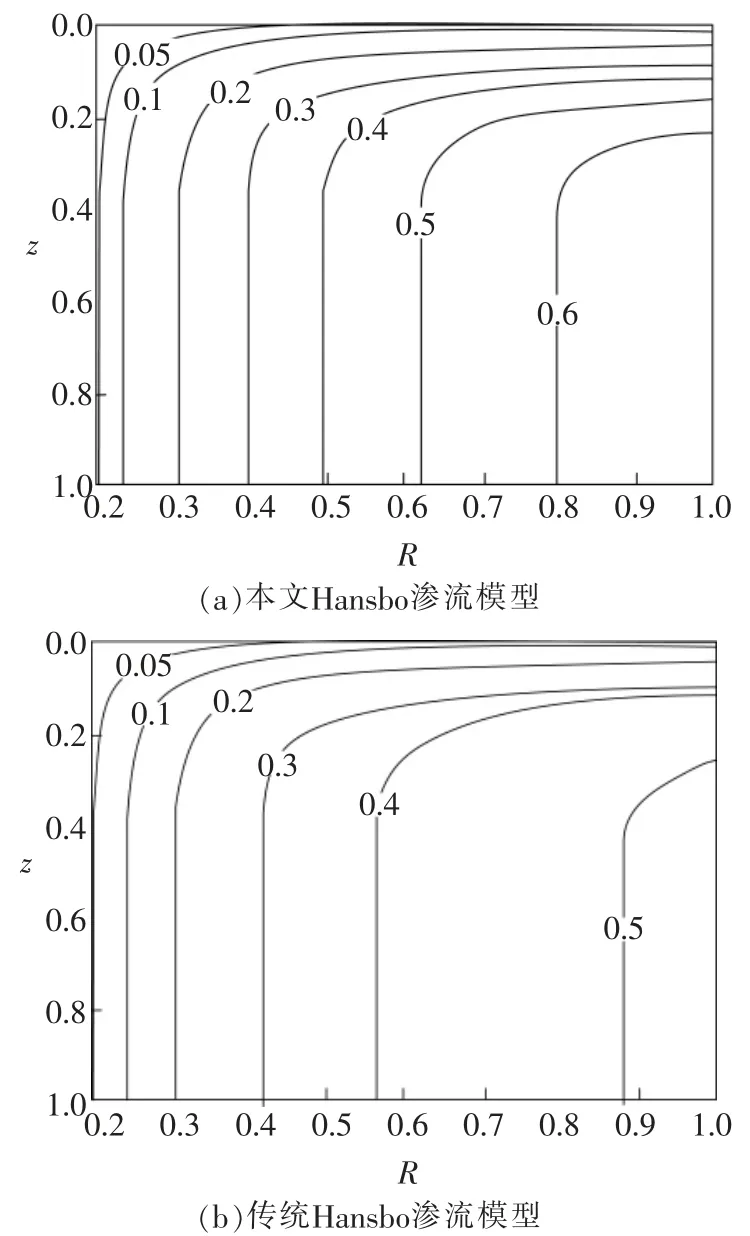
圖2 兩種模型超孔隙孔壓等值線對比

由圖2可以看出，在遠離排水面頂面處的超孔隙孔壓等值線幾乎都呈直線狀且平行于Z軸，說明這些地方的水力梯度的豎向變化量很小，相對應的滲流速度的豎向的分量也小。同時，還可以看出，本文建立的Hansbo滲流條件下的模型的超孔隙孔壓等值線的 “穩定區間” 明顯要比傳統Hansbo滲流模型法更長，說明本文建立的基于Hansbo滲流條件下的模型中，豎向排水引起的超孔隙孔壓減弱在整個黏土層的超孔隙孔壓消除過程中是次要的。值得借鑒的是，在砂井地基固結過程中可以通過進一步加大徑向排水來實現超孔隙壓力的快速消散。

3.2 對固結參數的影響

為了考察本文建立的砂井地基固化模型對砂井固結參數的影響，選取了以n=5，a=0.2的特征值條件下的實驗分析。

通過固結參數隨時間的變化曲線，發現當采用本文建立的砂井地基固化模型處理時，地基固化參數較小。說明本文建立的模型由于超孔隙孔壓消散較慢（穩定區間較長），導致整體固結參數較小，黏土層的固結時間增長。

根據對比結果，為了加快固結速度，需要加大本文建立的砂井地基固結模型的部分滲流參數。如加大滲流方程中m和i的值的大小，能夠使砂井固結方程的整體計算結果變大，固結速度就會變大。在實際應用中，如對固結質量有極高要求，那么需要再適當降低m和i值的大小。

3.3 對涂抹區因素的影響

在初始模型的建立過程中，假設了不考慮涂抹效應的條件，即無涂抹區（砂井形成時對砂井周邊土體產生擾動形成的擾動區）時的情況。由于實際砂井地基固結的情況，通常都含有涂抹區，需要重新考慮本文建立的砂井地基固化模型的準確性。

考慮到涂抹區滲流參數與砂井地基的滲流參數近似，因此分析時僅需注意涂抹區滲透參數K的改變。通過進行計算機數據模擬，能夠發現：若涂抹區的影響范圍較大，則在同一時刻砂井地基固化模型的平均固結參數會減小，且二者呈正線性關系，這表明涂抹區大小會影響砂井地基固化的速度；此外，在固結過程的中期階段，涂抹區對固結速度的影響達到最大值，而在地基固結的最后階段，涂抹區的影響逐漸消失。因此，若實際情況下的砂井地基固結需要考慮涂抹區影響，本文提出的基于Hansbo滲流法的砂井地基固結模型需要進一步的參數改進。

4 結語

在受到均勻分布載荷影響條件下，采用Hansbo滲流法建立的砂井地基固結模型來代替兩種傳統地基固化模型（基于Darcy滲流的傳統模型和Hansbo滲流傳統模型）的優化模型。通過采用有限元差分法的驗證和影響參數的分析，確定了該實驗數據模型的準確性和正確性。并得到了以下幾點結論：

（1）基于Hansbo滲流地基固化模型的土體凝固速度較傳統模型更慢，因此總體的固化時間會增長。但固化過程更加穩定，減小了傳統模型誤差發生率，同時，也可以通過滲流參數的簡單改變，來增大固結速度，且不會對其他參數和結果產生影響。

（2）地基固結時間與地基厚度成正比，地基厚度的增加會相應地增加地基固結時間。在不考慮涂抹區影響時，本文模型與傳統模型相差不大，但本文建立的固結模型更為精確。

（3）若需要考慮涂抹區的影響時，需要對本文模型進行適當的參數調整，如增大滲透區滲透參數K等。改變參數不會對其他計算和結果產生影響。

（4）在固結過程的前期和中期，涂抹區的影響和滲透參數對砂井地基固結平均速率的影響最大；而在固結后期，涂抹區的影響和滲透參數的影響可以忽略不計。