探析高考中概率統計系列試題及命題走向(下)
王慧興(特級教師)
3 概率應用
概率計算被廣泛應用于我們生活與生產當中,近些年高考命題無一例外地以概率計算為背景立意數學應用試題.但考查的知識點全部基于教材(如表4),堅持學什么考什么立意的命題原則.

表4 概率應用
3.1 隨機變量

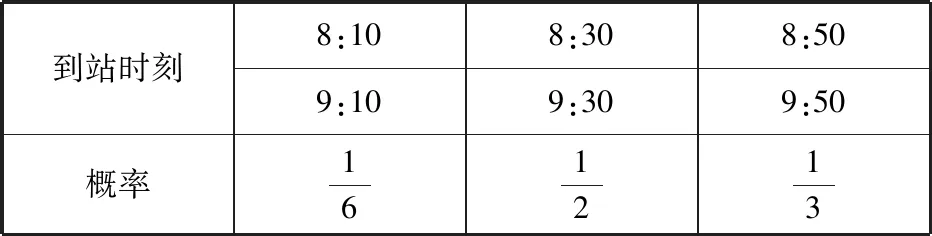
表5
一位旅客8:20到站,求他候車時間的數學期望.


表6
因此,該旅客候車時間X的數學期望為

(1)記20件產品中恰有2件不合格品的概率為f(p),求f(p)的最大值點p0.
(2)現對一箱產品檢驗了20件,結果恰有2件不合格品,以(1)中確定的p0作為p的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用.
(ⅰ) 若不對該箱余下的產品作檢驗,這一箱產品的檢驗費用與賠償費用的和記為X,求EX;
(ⅱ) 以檢驗費用與賠償費用和的期望值為決策依據,是否該對這箱余下的所有產品作檢驗.

令f′(p)=0,得p=0.1.當p∈(0,0.1)時,f′(p)>0;當p∈(0.1,1)時,f′(p)<0,所以f(p)的最大值點p0=0.1.
(2) 由(1)知,p=0.1.
(ⅰ) 令Y表示余下的180件產品中的不合格品件數,依題意知Y~B(180,0.1),則X=20×2+25Y,即X=40+25Y,所以EX=E(40+25Y)=40+25EY=490.
(ⅱ) 如果對余下的產品作檢驗,則這一箱產品所需要的檢驗費為400元,由(ⅰ)可知EX>400,故應該對余下的產品作檢驗.
3.2 統計分析

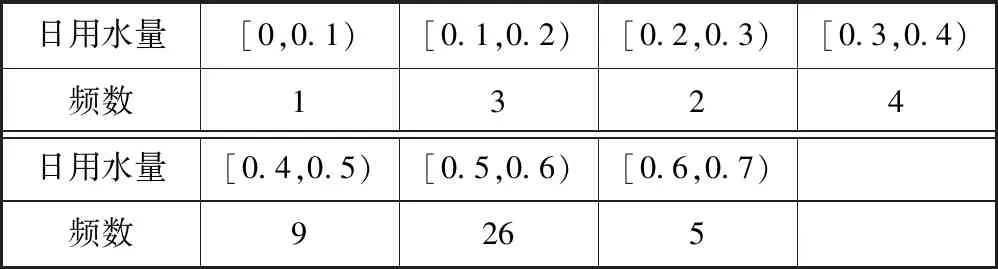
表7 未使用節水龍頭50天的日用水量頻數分布表

表8 使用了節水龍頭50天的日用水量頻數分布表
(1)作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖.
圖1
(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表).

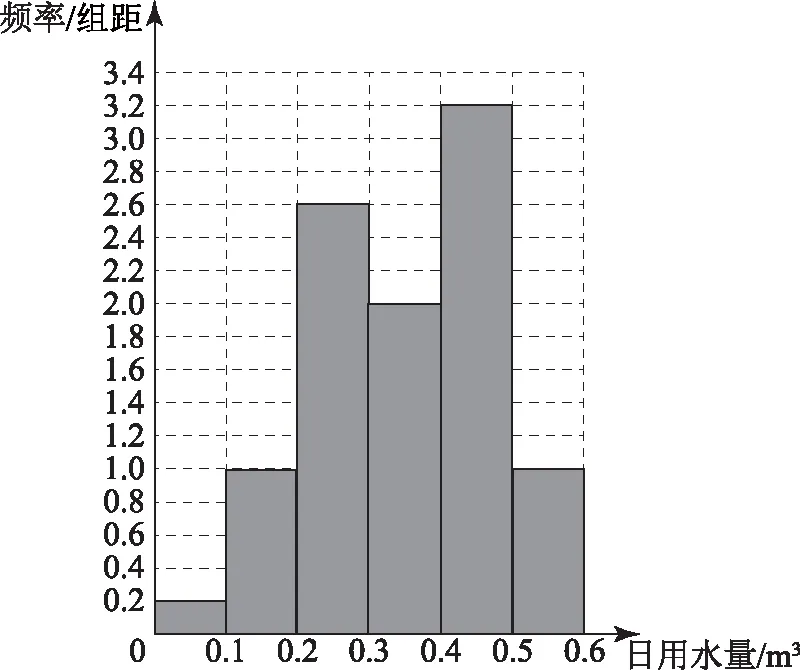
圖2
(2)根據圖2中的數據,易知該家庭使用節水龍頭后,日用水量小于0.35 m3的頻率為
0.2×0.1+1×0.1+2.6×0.1+2×0.05=0.48,
因此,該家庭使用節水龍頭后,日用水量小于0.35 m3的概率的估計值為0.48.
(3) 由題意知,該家庭未使用節水龍頭50天日用水量的平均數
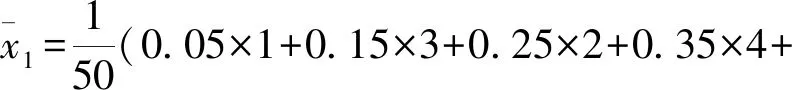
該家庭使用了節水龍頭后50天日用水量的平均數
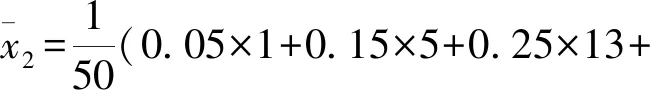
因此,估計該家庭使用節水龍頭后,一年可節省水(0.48-0.35)×365=47.45 m3.

(1)假設生產狀態正常,記X表示一天內抽取的16個零件中其尺寸在(μ-3σ,μ+3σ)之外的零件數,求P(X≥1)及X的數學期望;
(2)一天內抽檢零件中,如果出現了尺寸在(μ-3σ,μ+3σ)之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
(ⅰ) 試說明上述監控生產過程方法的合理性;
(ⅱ) 若檢驗員在一天內抽取的16個零件的尺寸如表9所示.

表9
經計算得
其中xi為抽取的第i個零件的尺寸,i=1,2,…,16.
附:若隨機變量Z服從正態分布N(μ,σ2),則
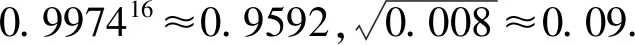

P(X≥1)=1-P(X=0)=1-0.997416≈0.0408.
X的數學期望EX=16×0.0026=0.0416.
(2) (ⅰ)如果生產狀態正常,一個零件尺寸在(μ-3σ,μ+3σ)之外的概率只有0.0026,一天內抽取的16個零件中,出現尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.0408,發生的概率很小.因此一旦發生這種情況,就有理由認為這條生產線在這一天的生產過程中可能出現了異常情況,需對當天的生產過程進行檢查,可見上述監控生產過程的方法是合理的.
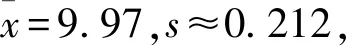
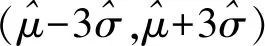
因此μ的估計值為10.02.
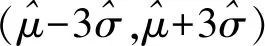
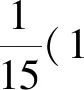
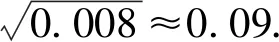
3.3 相關分析

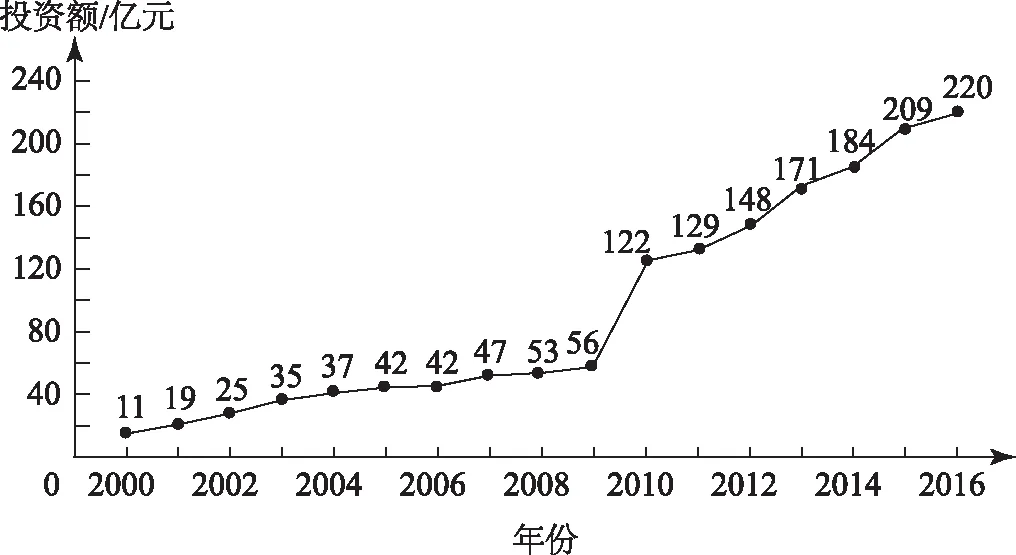
圖3
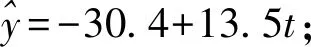
(1)分別利用這兩個模型,求該地區2018年的環境基礎設施投資額的預測值;
(2)你認為用哪個模型得到的預測值更可靠?并說明理由.

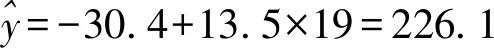
利用模型②,該地區2018年的環境基礎設施投資額的預測值為
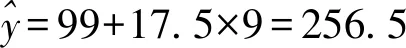
(2)利用模型②得到的預測值更可靠,理由如下.
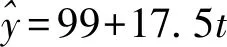
(ⅱ) 從計算結果看相對于2016年的環境基礎設施投資額220億元,由模型①得到的預測值226.1億元的增幅明顯偏低,而利用模型②得到的預測值增幅比較合理,說明利用模型②得到的預測值更可靠.
3.4 統計案例

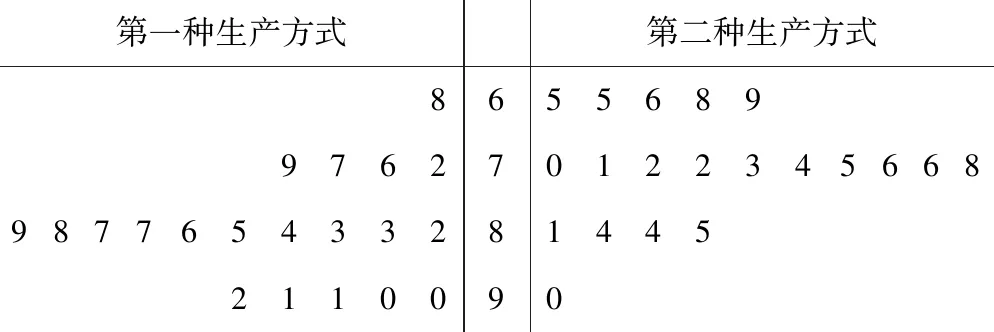
第一種生產方式第二種生產方式86556899762701223456689877654332814452110090
圖4
(1) 根據莖葉圖判斷哪種生產方式的效率更高,并說明理由;
(2) 求40名工人完成生產任務所需時間的中位數m,并將完成生產任務所需時間超過m和不超過m的工人數填入表10中.

表10
(3)根據(2)中的列聯表,能否有99%的把握認為兩種生產方式的效率有差異?
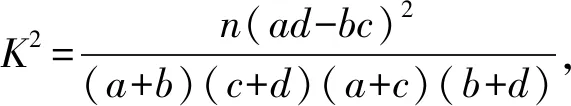

表11

(ⅰ) 由莖葉圖可知,用第一種生產方式,有75%的工人完成生產任務所需時間至少80min,用第二種生產方式,有75%的工人完成生產任務所需時間至多79min,因此,第二種生產方式的效率更高.
(ⅱ) 由莖葉圖可知,用第一種生產方式的工人完成生產任務所需時間的中位數為85.5min,用第二種生產方式的工人完成生產任務所需時間的中位數為73.5min,因此,第二種生產方式的效率更高.
(ⅲ) 由莖葉圖可知,用第一種生產方式的工人完成生產任務平均所需時間高于80min;用第二種生產方式的工人完成生產任務平均所需時間低于80min,因此,第二種生產方式的效率更高.
(ⅳ) 由莖葉圖可知,用第一種生產方式的工人完成生產任務所需時間分布在“莖8”上的最多,關于“莖8”大致呈對稱分布;用第二種生產方式的工人完成生產任務所需時間分布在“莖7”上的最多,關于“莖7”大致呈對稱分布,故可以認為用第二種生產方式完成生產任務所需的時間比用第一種生產方式完成生產任務所需的時間更少,因此第二種生產方式的效率更高.
以上給出的4種理由,考生答出其中任意1種或其他合理理由均可得分.

表12
4 數學建模
從數學學科核心素養看,數學建模是應用數學知識和方法解決實際問題的基本手段,也是推動數學發展的動力.高中數學教育肩負著發展學生關鍵能力、培育數學素養與提升數學境界的時代重任.因此,教師在教學設計時,應注重應用信息技術建構數學動態模擬試驗,以應對大數據時代的變化,引領學生學習數據處理方法,培養學生數據分析與計算能力,以教學方式轉變引領學生學習方式轉變.同時,高考命題已經直擊數學建模,以數學模型的方式檢測學生數據分析與數學計算能力,引領數學教育注重數學建模,以培育學生數學應用意識,概率統計問題一躍成為壓軸題就是一個明確的信號——數學建模真的來了. 從這一信號也可以預見隨著數學學科核心素養的深入落實,注定會將數學建模引入高考試題,同時也流露出將會從考查模型的方式命制試題.例如,由命題組構建一個數學模型,針對數據捕獲、數據分析與運算、檢驗與評價模型等進行考查,進而逐步把數學建模能力的考查引入高考試題.

(1)求X的分布列;
(2)若甲藥、乙藥在試驗開始時,都賦予4分,pi(i=0,1,2,…,8)表示“甲藥累積得分為i時,最終認為甲藥比乙藥更有效”的概率,則p0=0,p8=1,
pi=api-1+bpi+cpi+1(i=1,2,…,7),
其中a=P(X=-1),b=P(X=0),c=P(X=1).假定α=0.5,β=0.8.
(ⅰ) 證明:{pi+1-pi}(i=0,1,2,…,7)為等比數列;
(ⅱ) 求p4,并由p4值解釋該試驗方案的合理性.

P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β).
隨機變量X的分布列如表13所示.
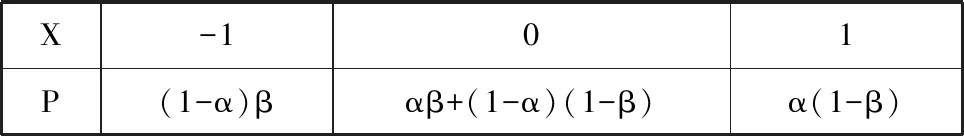
表13
(2) 根據(1)可得

即pi+1=5pi-4pi-1(i=1,2,…,7).
①
(ⅰ) 對①作同構轉化,得
pi+1-pi=4(pi-pi-1) (i=1,2,…,7).
若p1-p0=0,則pi-pi-1=0,?1≤i≤8,所以{pn}是常數列,1=p8=p0=0矛盾,故p1-p0≠0,所以{pi+1-pi}(i=0,1,2,…,7)是公比為4,首項為p1的等比數列.
(ⅱ) 由增量恒等式,得
②
③
由②③消去p1,得
由試驗數據得出p4≈0.00389,按其定義p4=P(∑X+4=4)=P(∑X=0),表示在甲藥累計得0分,被認為比乙藥更有效的概率是0.00389,這是一個小概率事件,表明試驗數據與甲、乙兩種新藥的統計數據“甲藥治愈率為0.5,乙藥治愈率為0.8”相符(在甲藥治愈率明顯低于乙藥治愈率的前提下,試驗得出甲藥反而更有效,這種可能性應該很小,也就是錯誤判斷兩種藥物有效性的概率極低),因此,該試驗方案合理.
簡評本題是以新藥效果試驗為題根的數學應用問題,題目新穎別致,替代導數應用問題作為試卷壓軸題,釋放來年新高考信號:數學建模將引入新高考試卷,很可能會繼續作為壓軸題出現. 但題目給出數據pi的關系式,學生一不小心就會看錯題,有一定的誤導性. 如果把已知p0,p8以及數列{pi}的遞推關系改為由學生建立,既能回避這個問題,更能深入檢測學生對數學本質的理解.
事實上,每一輪試驗兩種藥物得分之和都是0分,所以兩種藥物累計得分一直是8分,p0表示“甲藥的累積得分為0時,最終認為甲藥比乙藥更有效”的概率,這時,乙藥累計得分恰好是8分,因此乙藥比甲藥多治愈4只小白鼠,試驗停止,所以這時甲藥被認為比乙藥更有效的概率是0,即p0=0.同理,p8=1.
因為甲藥累計得分為i對應的事件是3個事件的和事件:甲藥累計得分為i-1,再進行一輪試驗,甲藥又得1分,由每輪試驗的獨立性,可知這一事件的概率為p(X=1)·pi-1=a·pi-1;甲藥累計得分為i,再進行一輪試驗,甲、乙均得0分,這一事件概率為p(X=0)·pi=b·pi;甲藥累計得分為i+1分,再進行一輪試驗,甲藥得-1分,這一事件的概率為p(X=-1)·pi+1=c·pi+1. 由互斥性,可得pi=api-1+bpi+cpi+1(i=1,2,…,7)(注意:這個構建過程本質上是基于全概率公式,但由獨立性,相應的條件概率簡化了).
2010年,蘇淳教授也命制過一個“漂亮”的模型檢驗試題,如例15.

現設n=4,分別以a1,a2,a3,a4表示第一次排序時被排為1,2,3,4的四種酒在第二次排序時的序號,并令X=|1-a1|+|2-a2|+|3-a3|+|4-a4|,則X是對兩次排序的偏離程度的一種描述.
(1)寫出X的可能值集合;
(2)假設a1,a2,a3,a4等可能地為1,2,3,4的各種排列,求X的分布列;
(3)某品酒師在相繼進行的三輪測試中,都有X≤2.
(ⅰ)試按(2)中的結果,計算出現這種現象的概率(假定各輪測試相互獨立);
(ⅱ)你認為該品酒師的酒味鑒別功能如何?說明理由.

在1,2,3,4中奇數與偶數各有兩個,所以a2,a4中的奇數個數等于a1,a3中的偶數個數,因此|1-a1|+|3-a3|與|2-a2|+|4-a4|的奇偶性相同,從而X=(|1-a2|+|3-a3|)+(|2-a2|+|4-a4|)必為偶數.X的值非負,且易知其值不大于8,所以X的可能取值的集合為{0,2,4,6,8}.
(2)可用列表或樹狀圖列出1,2,3,4的24種排列,計算每種排列下的X值,在等可能的假定下,得到X的分布列,如表14所示.
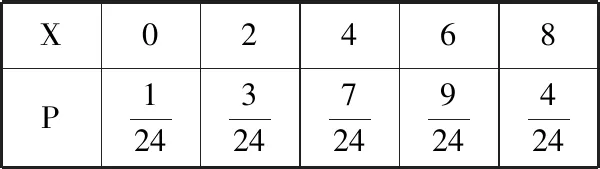
表14
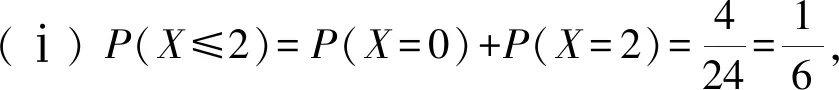
5 結束語
2019年高考數學試卷出現較多變化,教師需要根據這些變化進行適度調整,為2020年的新高考做準備,譬如解答題的壓軸題可能要從導數應用調整為以概率統計為主干的數學建模,重在對概率問題的理解與分析. 這一重大變化釋放出改革信號——全面落實數學學科核心素養下的高考壓軸題將以概率統計為載體,對數學建模進行考查,流露出概率與統計系列試題的走向. 高考基于實際情境立意、真實地提出數學問題,引導學生應用數學知識與方法解決身邊問題,達到立德樹人、五育并舉、助力德智體美勞全面發展的目的,同時,又能激發學生對試題的親切感、成就感與自豪感. 在一定程度上助推素質教育,扭轉以應試為主的目標教學,營造整體把握數學知識與方法的教學環境.

