基于遺傳算法的工廠AGV路徑優化研究

黨宏社 孫心妍

摘要：針對工廠AGV行駛路徑復雜、應用局限性等問題，vRAGV配送物料行駛路徑最短為目標，采用遺傳算法進行AGV路徑規劃，并加入物料類型選擇的循環套，通過多次實驗確定最合理的控制參數，從而產生AGV運輸多種類型物料的最優路徑結果。使用Maflab軟件對算法進行仿真，結果表明：該算法是有效的，能夠直接實現ACV在輸多種類型物料時所產生的不同種路徑的優化。

關鍵詞：自動導引車;路徑規劃;遺傳算法

0引言

隨著社會生產技術的發展和自動化程度的提高，很多工廠為了提升運輸工作效率，引入了自動導引小車AGV（Automatic Guided Vehicle）進行物流運輸。據相關資料統計，在制造業中不足5%的時間用于加工裝配，而超過95%的時間用于物流配送，因此物料的及時準確供應直接關系到生產線的流暢性。節約車間生產成本，減少物料運輸時間，提升單臺AGV搬運效率，一直以來AGV的路徑規劃問題，即尋找AGV的最優路徑是工廠所關注的焦點。

目前國內外很多學者都對于AGV的路徑規劃問題做了相應的研究。遺傳算法是模仿自然界生物進化機制發展起來的隨機全局搜索優化方法，具有算法效率高、魯棒性強、可實現并行搜索等特點，被廣泛用于解決路徑規劃等領域的問題。G.Jeon和William等人用混合遺傳算法求解車輛路徑規劃問題：李青欣進行了AGV路徑規劃的遺傳算法研究，根據運行環境信息復雜度和數量的不同分別分析了幾種不同類型的路徑規劃。

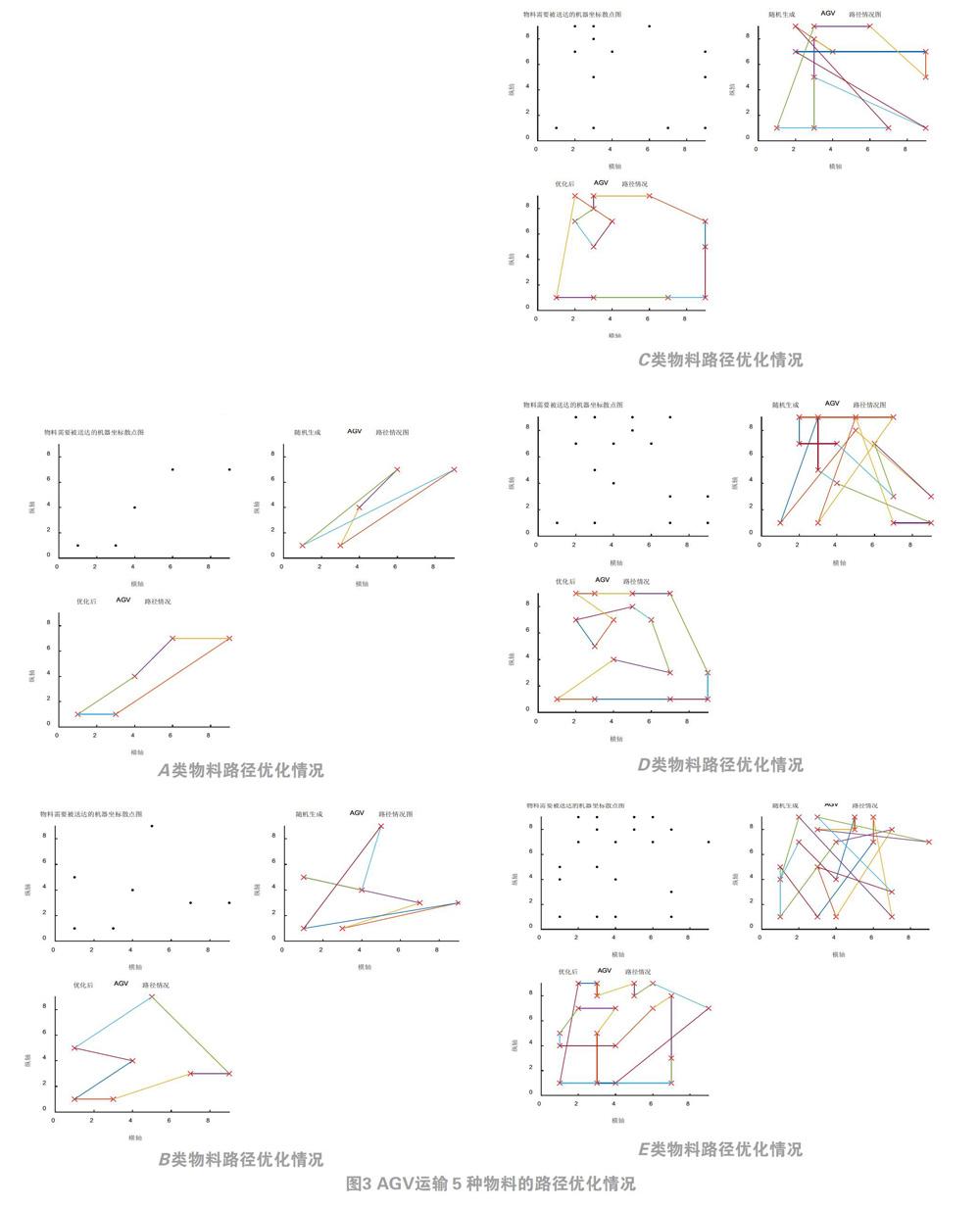
當前國內外學者在AGV的路徑規劃問題上取得了諸多成果，但是實際的工廠生產情況多變，機器所需的物料并不相同，因而AGV的運輸路徑也有差異。……