基于上證50ETF期權的“定價核之謎”研究

(東北財經大學應用金融與行為科學學院，遼寧 大連 116025)

一、引言

定價核(Pricing Kernel)又被稱為隨機折現因子(Stochastic Discount Factor)，自被提出以來在資產定價領域具有極其重要的地位(Lucas，1978)[18]，是構成資產定價大廈不可或缺的一塊基石。通過求解定價核，可以將所有資產定價理論納入一個一般化模型，進而為所有金融資產定價。同時，定價核包含了投資者在不同狀態下效用評估的重要信息，通過研究定價核可以反映投資者對市場未來不同情況的預期。

在理性投資者與完全市場等基本假設下，Dybvig(1988)[11]理論上證明了定價核是經濟總財富的單調遞減函數。但Ait-Sahalia and Lo(1998)[1]，Jackwerth(2000)[17]及Rosenberg and Engle(2002)[20]基于美國市場數據的經驗研究表明，定價核具有局部增加的特性，經驗證據與理論結果相悖。這一現象后來被稱為“定價核之謎”(Pricing Kernel Puzzle)(Brown and Jackwerth, 2012)[6]。隨后，諸多學者采用不同金融市場的數據與不同方法證實了“定價核之謎”的存在，其中對美國金融市場的研究占絕大多數(Beare and Schmidt，2014；Cuesdeanu et al., 2017；Bali et al., 2017)[4][10][2]，對德國市場與香港市場同樣有學者給出了“定價核之謎”存在的經驗證據(Golubev et al.，2014；吳鑫育，2015)[13][23]；另外，也有學者認為如果對投資者效用函數的形式進行限制，“定價核之謎”就不存在(Chernov and Ghysels, 2000)[9]。

盡管現有文獻對于境外主要發達市場的定價核均有研究，但對國內市場定價核的研究幾乎為零。中國市場是股票市值排名第二的大市場，在國際金融市場中的地位與影響愈發重要，因此給出“定價核之謎”在中國市場是否存在的實證證據，對我國資產定價領域的研究具有極其重要的意義。同時，鑒于中國金融市場與發達金融市場在投資者與制度等方面存在諸多差異，如能給出“定價核之謎”在中國存在的經驗證據，將會進一步為“定價核之謎”提供實證支持。

在“定價核之謎”被大量經驗研究證實存在后，有學者研究了“定價核之謎”的形成原因。如果金融市場不能滿足市場完整、投資者風險厭惡且具有一致的正確信念，就可能出現“定價核之謎”(Hens and Reichlin,2012)[15]，另外有學者認為波動率可能是導致“定價核之謎”的原因(Song and Xiu，2016；Giacomini et al., 2008；Grith et al., 2013)[21][12][14]。不難發現“定價核之謎”包含了市場中一些隱藏的重要信息，但鮮有文獻著眼于“定價核之謎”與市場表現之間存在何種關系。本文在對“定價核之謎”與市場走勢的特征事實進行觀察后，發現兩者之間確實存在一定相關性，提出猜想“當期出現定價核之謎會預示下期市場出現震蕩或下跌”，隨后將Hens and Reichlin(2012)[15]的研究結果與“定價核之謎”成因會對市場造成影響的實證證據(鄭振龍和孫清泉，2013；陳國進和張貽軍，2009)[24][22]相結合，給出了猜想成立的理論支持，最后通過計量方法證實了上述猜想。

總的來說，本文首先選取上證50ETF日度收盤價來計算客觀風險概率密度，并根據上證50ETF期權計算風險中性概率密度，求解得到經驗定價核。隨后對中國市場是否存在“定價核之謎”進行檢驗，根據Beare and Schmidt(2014)[4]的統計框架，本文構建了定價核單調性統計量，對所有月份的定價核進行統計檢驗。結果表明，在95%的置信水平下，可以在18%的月份1里拒絕定價核單調遞減，即存在“定價核之謎”。最后，本文對定價核與上證50ETF走勢之間的關系進行了分析，結果顯示，“定價核之謎”與下期市場收益率呈反向關系、與下期市場振幅呈正向關系。

本文的主要貢獻有以下兩點：第一，首次給出了“定價核之謎”在中國金融市場存在的經驗證據；第二，創新性地將“定價核之謎”與下期市場走勢聯系起來，在給出兩者之間具有相關性的理論支持后，通過實證檢驗證實了“定價核之謎”對未來市場走勢有一定的預測作用。

二、研究方法

(一)定價核的測算

通過對現有文獻進行梳理，可以將定價核的估算方法大致分為兩類。第一類方法是從計量經濟學的角度進行研究，將定價核看作是所有個體稟賦聚合成一個整體的函數進行求解，其中具有代表性的例子為Chapman(1997)[8]等人的研究。第二類方法基于無套利原則，從資產定價的視角對定價核進行估算，其中具有代表性的例子為Rosenberg and Engle(2002)[20]、Beare and Schmidt(2014)[4]等人的研究。由于第一類方法中所需的總消費數據需要運用宏觀經濟數據來計算，而宏觀數據的測量誤差較大，因此定價核的估計存在較大誤差。所以本文采取第二類方法，采用Monteiro et al.(2008)[19]提出的三次樣條模型近似得到風險中性密度函數。該方法兼具靈活和參數化的優點，可以很好地擬合風險中性概率密度，進而計算得到定價核。

從定價核的基本表達式出發，若Yt為t期資產Y的價格，zt+1為t+1期資產的支付，Mt為當期定價核，則資產Y的定價公式如式(1)所示：

求解定價核的核心思想為“同一資產在不同概率測度下計算出的價格應當一致”。現考慮一個在t時期發行的或有要求權資產(如指數期權)，其在t+1期的支付為zt+1=ft(xt+1)，ft為標的指數的支付函數，xt+1為t+1期指數收益率。那么在風險中性概率測度Q下，該種資產在t期的價格為：

式(2)中的qt為該期關于標的指數收益率的風險中性概率密度(risk-neutral density)，rt為當期無風險利率。

在客觀概率測度P下，由期望的迭代法則可推得該種資產在t期的價格為：

式(3)中的pt為該期關于標的指數收益率的客觀概率密度(physical density)，πt為剝離了無風險折現率的定價核(在本文以下部分所指定價核均為πt形式)。將式(2)與式(3)聯立，即可得到定價核πt的表達式(4)，在下面本文將分別給出pt和qt的計算方法。

1.客觀概率密度pt的計算

本文參照Rosenberg and Engle(2002)[20]的方法對客觀概率密度pt進行求解，具體步驟如下：

首先，對于使用標的指數數據描述股票指數收益時間序列變化過程，本文使用具有經驗新息密度(empirical innovation density)的GARCH模型，模型的具體形式如下：

其次，在估計得到GARCH模型的參數后，通過將新息密度分解為時變和恒定的部分來模擬經驗新息密度f。定義“標準化新息”為收益率新息εt與其條件標準差σt|t-1的比率，標準化新息密度(εt/σt|t-1)——即標準化新息集合——是經驗新息密度的恒定成分。條件標準差(σt|t-1)是經驗新息密度的時變分量。計算出的標準化新息的集合構成了經驗密度函數，它可以體現出在實際金融市場中出現的過度偏斜、峰度和其他不能在正態分布下體現的特征。

最后，通過模特卡羅方法模擬整個周期收益率路徑來求解客觀概率分布。在根據單周期的模擬方法得到當期收益率與收益率新息εt+1后更新條件方差σt+2|t+1，進而得到第二個周期的回歸新息εt+2，隨后再更新條件方差σt+3|t+2，…，直至最后一期，最終得到多期對數收益率模擬值∑n i=1(μ+rf+εt+i)與多周期簡單回報的模擬值{exp[∑ni=1(μ+rf+εt+i)]-1}。重復此步驟20,000次，得到整個周期的客觀概率分布。

2.風險中性概率密度qt的計算

通常，對風險中性概率密度的計算可分為以下三種方法：(1)第一種方法對標的資產價格的變動模式進行了較強的假設，隨后使用數值方法求解風險中性概率密度(吳鑫育，2015)[23]；(2)使用非參數方法估計風險中性概率密度Q(Ait-Sahalia and Lo, 1998)[1]；(3)首先對風險中性概率密度的分布進行設定，隨后通過參數化的方法對其進行求解(Rosenberg and Engle，2002；Beare and Schmidt,2014)[20][4]。本文在第三種方法的基礎上，依據Monteiro et al.(2008)[19]的方法使用三次樣條近似風險中性密度函數。該方法在汲取前兩種方法優點的同時，規避了他們的缺點，使結果兼具參數化與靈活性。

首先，構建三次樣條風險中性密度的表達式，設風險中性密度q是在區間(x0,xk]上具有k個子區間與k+1個固定節點的三次樣條(即平滑的分段三次多項式)。節點的選擇是任意的，本文根據當期的條件波動率來選擇結點的位置與個數，具體做法詳見實證部分。給定節點的位置后，q可以寫成式(7)的形式。

同時q(x;θ)需要滿足如下條件：(1)概率密度函數q在整個區間積分要求等于1；(2)函數在各個端點處連續且二次可導；(3)函數在左右端點x0和xk處連續并且等于零；(4)函數在區間內為非負函數。

其次，求得使以交易量vi加權的市場價格wi與用風險中性密度q擬合的價格之差的平方和最小的最優參數θm，用交易量加權的做法源于高頻交易資產更有可能反映出準確的定價。參數θm的表達式為

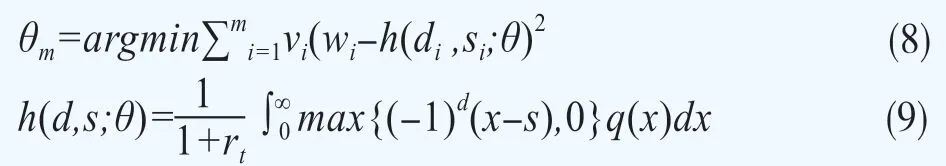
其中di為期權的行權方向，di=1為看漲，di=0為看跌；si為期權的行權價格；rt為當期的無風險利率。

最后，將估計出的參數θm代回風險中性密度q的表達式，估計完成。

(二)統計檢驗

本文按照Beare and Schmidt(2014)[4]的統計檢驗方法，通過計算序數優勢曲線(Ordinal Dominance Curve)與最小凹面主函數(Least Concave Majorant)之間的距離構建檢驗統計量，對定價核的單調性進行統計檢驗。首先，建立原假設與備擇假設：

H0：定價核是非增的

H1：定價核不是非增的

單調性檢驗方法的基本原理是基于定價核π的單調性與序數優勢曲線的凹度之間的等價關系。首先對前文所得q與p進行積分，可獲得對應的累計概率分布函數Q與P，設m表示當期觀察到的期權合約數量，n表示時間序列的長度，將Qm和Pn作為Q和P的樣本大小為m和n的無偏估計值。給定對Qm和Pn，本文構造相應的序數優勢曲線?m,n:[0, 1]→[0, 1]如下：

構造?m,n的最小凹度主函數M?m,n，該函數定義為最小的且處處大于等于?m,n(u)的凹函數。最后，通過M?m,n與?m,n之差的構建檢驗統計量來對原假設與備擇假設進行檢驗：

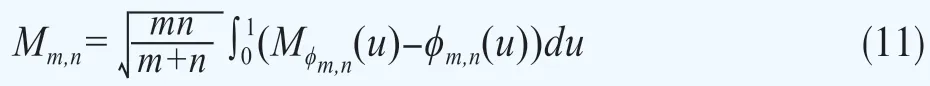
三、實證檢驗

(一)樣本選取和變量定義

本文使用在上海證券交易所交易的上證50ETF期權數據估算風險中性概率密度，樣本區間為2015年2月9日至2019年4月1日，共計118,146個期權合約的交易數據，數據來源于Wind資訊。在實證研究中，本文對樣本數據進行了如下篩選：(1)剔除成交量為0的期權數據；(2)剔除在值程度小于0.85和大于1.15的看漲期權數據；(3)剔除在值程度大于1.15和小于0.85的看跌期權數據。經篩選后，獲得滿足條件的期權合約數量1025個。隨后，從期權當日行情數據與合約標的數據中提取風險中性概率密度計算所需的d-行權方向、v-當日交易量、w-市場價格、s-行權價格，計算風險中性概率密度。

對于期權標的價格數據，本文選取2005年1月1日至2019年4月1日的上證50ETF后復權收盤價，用當日收盤價St除以前一日收盤價St-1取對數得到當日對數收益率，計算客觀概率密度。

在后文驗證定價核之謎與市場相關性時，本文用下期上證50ETF的對數收益率與振幅對衡量定價核之謎程度的定價核非單調遞減統計量進行了回歸，選取股市流動性指標與實現波動率作為控制變量，相關變量的含義和定義式如表1所示，上證50ETF數據與所選取回歸變量均來源于Wind資訊。

表1 變量的定義

(二)定價核計算結果

1.P測度的計算結果

本文采用經驗概率分布的GARCH模型對上證50ETF的對數收益率序列進行建模，進一步應用蒙特卡洛模擬的方法模擬出未來一個月的客觀概率密度。首先，采用ADF方法對上證50ETF對數收益率序列進行平穩性檢驗，結果表明上證50ETF對數收益率是平穩序列。其次，對均值方程的殘差項進行分析，發現收益率殘差的分布與正態分布并不匹配。最后，應用Ljung-Box混成檢驗方法對殘差進行ARCH效應檢驗，結果發現各階滯后項的p值都接近于0，認為殘差的平方序列存在顯著的自相關性，同時也說明序列存在很強的ARCH效應。

雖然殘差并不滿足正態分布的特征，但根據Bollerslev and Wooldridge(1992)[5]的研究結果，即使真正的新息密度是非正態的，使用正態假設的GARCH模型也能提供一致的參數估計。所以，本文采用標準的GARCH模型對收益率時間序列進行擬合，通過比較不同階數的AIC與BIC值，本文最終采用GARCH(1, 1)模型，擬合結果如表2所示。

從表2的結果可以看出，均值方程中的系數接近0，條件波動率方程中前一期新息的系數為0.1，前一期條件標準差的系數為0.88，說明當期條件波動率確實與前一期相關，選擇GARCH模型對收益率時間序列進行擬合是合理的。將條件標準差與標準化新息密度相乘，獲得該期的經驗概率分布。將符合經驗概率分布的信息替換原有的正態分布新息，得到經驗概率分布的GARCH模型：

最后，本文運用經驗概率分布的GARCH模型，在每個月的特定日期運用蒙特卡洛方法模擬未來一個月的對數收益率，并重復20,000次，進而獲得基于估計日所能獲得信息對一個月后客觀概率密度曲線的估計。

表2 上證50ETF對數收益率GARCH模型擬合結果

2.Q測度的計算結果

本部分采用風險中性概率密度的三次樣條插值模型對上證50ETF期權的交易收盤價進行參數擬合，求得最優參數后代入模型，最終得到風險中性概率密度。基于前文對客觀概率密度的估計，以下月到期日當日價格估計分布的條件標準差為基準，確定風險中性概率密度的最優區間與子區間。具體而言，本文按照式(13)確立節點的位置及個數，其中S0為估計當日的標的收盤價，a=[3.25 2.25 1.5 1 0.5 0]2。

本文采用Monteiro et al.(2008)[19]等人提供的一種基于半定規劃的方法對參數θm進行求解，最后代入式(8)得到風險中性概率密度q。為對擬合結果進行檢驗，本文利用得到的風險中性概率密度曲線計算期權的擬合價格，并計算其與市場價格的偏離程度，誤差為17.7%3，可認為擬合出的風險中性概率密度很好地提取了期權市場價格中所包含的信息。

3.實證定價核的計算結果

基于前文客觀概率p與風險中性概率密度q的計算結果，對定價核進行求解。由于在市場的某些特殊時期投資者情緒過激，位于分布尾端的風險中性概率密度曲線與客觀概率密度曲線差異過大，導致定價核出現指數型暴增，失去了實際意義，對于該種情況本文截取月漲跌幅在20%以內的范圍對定價核進行求解，使得定價核的結果便于橫向比較，更具實際意義。基于當月數據求解的下月定價核結果如圖1所示(50期，2015年3月～2019年4月)。

對圖1中定價核的形狀進行直觀觀察可以發現，大部分定價核都呈現出單調遞減的形式，個別月份的定價核呈現局部遞增與U型定價核的情況，但是這一結論僅是直接觀測出的，沒有相關理論與數據支持，所以本文在下節進一步研究定價核的單調性，通過構建檢驗統計量，在統計層面上給出定價核之謎是否存在的結論。

圖1 實證定價核結果

(三)統計檢驗結果

基于本文研究方法(二)中的統計框架，本節首先求得每個定價核對應的序數優勢曲線?m,n，在此基礎上做出每條序數優勢曲線?m,n對應的最小凹度主函數，結果如圖2所示。

基于圖2中兩條曲線之差的積分，即圖中的陰影部分，構建定價核非單調遞減的統計量M如表3所示。

依據理論部分對臨界值的計算方法，本文通過蒙特卡洛模擬方法得到了檢驗統計量的臨界值。在95%的置信度下，拒絕值為0.063。根據結果，在95%的置信度下，整個時間區間內18%月份的定價核是非單調遞減的，即存在“定價核之謎”。

圖2 序數優勢曲線與最小凹度主函數

表3 月度定價核非單調遞減統計量

四、進一步研究

(一)“定價核之謎”與市場走勢相關性的特征事實與猜想的提出

為進一步研究“定價核之謎”，本文將估算得到的定價核時間序列與市場走勢放在一起進行對比，對兩者之間的相關性進行分析。首先，本文對上證指數從2015年初到2019年中的走勢進行了總結。通過對比指數走勢與定價核的時間序列，發現當定價核呈現出較大程度的U型或局部遞增程度很大(即定價核的非單調性異常顯著)時，下月市場往往會出現不同程度的大幅下跌或震蕩，如表4所示。

基于以上事例，本文提出如下猜想：“定價核之謎”的出現往往預示著下期市場將出現大幅下跌或震蕩。為驗證這一猜想是否合理并具有一般性，下面本文將給出該猜想的理論支持，并用下期上證50ETTF對數收益率與振幅對能夠衡量“定價核之謎”程度的定價核非單調遞減統計量進行回歸，進行實證檢驗。

(二)猜想的相關理論支持

根據Hens and Reichlin(2012)[15]的理論推導，“投資者的風險尋求行為”(高估尾部事件概率)與“不完全市場和異質信念”導致的定價核中遞增部分，可能是導致“定價核之謎”的潛在原因。進一步，本文將分析導致定價核之謎潛在原因與市場走勢之間存在何種相關性。

1.“投資者的風險尋求行為”(高估尾部事件概率)與市場收益之間的關系

Brunnermeier et al.(2007)[7]指出過度自信會使投資者的主觀概率偏離客觀概率，過于重視尾部事件發生的概率。Barberis and Huang(2008)[3]在前景理論的基礎上，認為投資者會對資產收益分布的兩端賦予較高的概率權重。這些研究都表明投資者存在高估極端事件概率的心理，持有彩票類股票能提高其預期效用，并愿為彩票類股票支付較高的價格，從而導致賭博偏好的風險收益為負。鄭振龍和孫清泉(2013)[24]選用Fama-French三因子模型作為基準定價模型來考察中國股市中彩票類股票組合的相對收益表現，結果表明，與“非彩票類股票”和“其他股票”相比，在我國股市上投資“彩票類股票”的相對收益為負且顯著。綜上，在中國市場投資者高估尾部事件概率這一特征與風險回報呈負相關系。

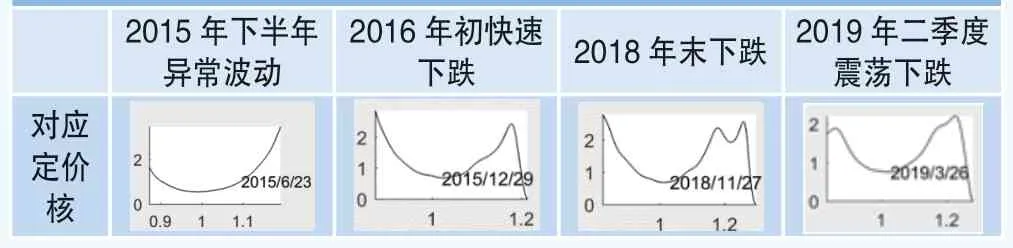
表4 2015年至今大幅震蕩或下跌時期對應定價核

2.“不完整的市場和異質信念”與市場收益之間的關系

Hong and Stein(2003)[16]根據行為金融理論的框架，認為投資者的過度自信會導致異質信念的產生，并從投資者具有異質信念與市場存在賣空限制這兩個角度，論證了暴跌的產生原因，以及暴跌為什么具有傳染性。由他們的理論模型分析可知，在市場存在賣空限制的背景下，投資者的異質信念會導致壞信息不能及時被投資者知曉，從而造成大范圍的暴跌。陳國進和張貽軍(2009)[22]基于中國股票市場對異質信念、賣空限制與股價行為進行了研究，結果表明，異質信念與不完全市場的存在會導致市場會出現暴漲暴跌、大幅震蕩，且暴跌的影響更大。

由此，無論導致定價核之謎的成因是“投資者高估尾部概率”還是“不完整的市場和異質信念”，本文都找到了其與市場收益負相關并會導致市場震蕩的證據，進而給出了“定價核之謎”會預期下期市場出現震蕩或下跌的理論支持。

(三)猜想的實證檢驗結果

為給出猜想的實證檢驗結果，本文首先關注“定價核之謎”對下期市場收益率的影響，用下一期的對數收益率對當期定價核非單調遞減統計量進行回歸。為樣本匹配，被解釋變量使用t+1期，解釋變量使用t期，控制變量使用t期，其中式(15)為在式(14)的基礎上添加了實現波動率與流動性指標兩個控制變量。

回歸結果如表5所示，其中Mt為衡量“定價核之謎”顯著程度的統計量。

從方程(14)的回歸結果可以看出，定價核非單調統計量的系數為-0.163且在1%顯著性水平顯著(t=-2.83)，說明定價核的非單調遞減統計量對下一期收益率有顯著的負向影響；在方程(15)中，控制了波動率和流動性指標之后，定價核非單調遞減統計量的系數在10%的顯著性水平下依然為負(t=-1.72)，這說明“定價核之謎”對下期市場收益率確實有負向影響，與本文的猜想一致。時間序列回歸易產生“偽回歸”問題，因此本文對回歸的殘差序列進行了ADF檢驗，檢驗結果表明方程(14)與方程(15)的ADF檢驗統計量分別為-8.1897與-8.2517，均小于1%顯著性水平的Mackinnon臨界值-3.435，因此殘差序列是平穩的，上述回歸結果不存在偽回歸問題。

表5 當期定價核與下期市場收益率的回歸結果

再用振幅對當期定價核非單調遞減統計量進行回歸，同樣選擇實現波動率與流動性指標作為控制變量，回歸結果如表6所示。

從方程(16)的回歸結果可以看出，定價核非單調遞減統計量的系數為0.619且在1%顯著性水平下顯著(t=5.78)，說明定價核非單調遞減性統計量對下一期振幅有顯著的正向影響；在方程(17)中，控制了波動率和流動性之后，定價核非單調統計量的系數依然在1%顯著性水平下為正(t=3.38)，這說明“定價核之謎”對下期市場振幅確實有正向影響，與本文的猜想一致。同樣對“偽回歸”問題進行了檢驗，方程(16)與方程(17)殘差的ADF檢驗統計量分別為-7.2802與-4.3386，均小于1%顯著性水平的Mackinnon臨界值-3.435，上述回歸結果不存在偽回歸問題。

綜上，本文運用下期市場對數收益率與振幅對能夠衡量定價核之謎的定價核非單調遞減統計量分別進行了回歸，結果表明定價核之謎的出現與下期市場收益率呈顯著的負向關系，與下期市場振幅呈顯著的正向關系，并且再加入了控制變量后依舊顯著。這一實證結果證實了本文提出的猜想。

表6 當期定價核與下期市場振幅的回歸結果

五、結論

本文首先利用具有經驗概率分布新息的GARCH模型對上證50ETF對數收益率進行模擬來計算客觀風險概率密度。接下來，利用GARCH模型得到的條件波動率確立風險中性概率分布的分布區間并構建三次樣條插值的風險中性概率密度參數模型，利用市場上觀測到的期權數據(交易量、行權方向、行權價格、收盤價格)對模型參數進行估計，代入原模型得到風險中性概率密度。將風險中性概率密度與客觀概率密度相除，本文獲得了中國市場的月度定價核。觀察發現大部分時間定價核表現出了單調遞減的形式，在某些特殊時期定價核呈現出了局部遞增或U型的特征。隨后，為更準確地檢驗“定價核之謎”，本文構建了單調性統計量，對所有月份的定價核進行單調性檢驗。結果表明，在95%的置信水平下，可以在18%的月份里拒絕定價核單調遞減，從而首次給出了“定價核之謎”在中國市場存在的經驗證據。最后，本文對定價核與上證50ETF走勢之間的關系進行了分析，提出猜想——“定價核之謎”的出現往往預示著市場下期走勢會出現震蕩或下跌。為驗證這一現象，本文用下期市場收益率、振幅對定價核非單調遞減統計量進行了回歸，結果表明非單調性統計量是顯著的，“定價核之謎”與下期市場收益率呈反向關系、與下期市場振幅呈正向關系。

注釋

1.根據投資者預期短時間內(一個月)不變的假定，本文選擇對月度定價核進行計算。

2.a值的選取是任意的，實證結果表明按該a值劃分區間計算得到的風險中性概率密度是最優的。

3.限于篇幅限制未給出期權擬合價格與實際市場價格誤差的計算結果，如有需求，可向作者索要。