拖曳陣被動合成孔徑目標深度穩健估計?

李天宇 李 宇 黃海寧 遲 騁

0 引言

目標深度估計在水下目標探測識別領域發揮著越來越重要的作用，同時也面臨著信息獲取難度大和環境影響復雜等多方面的困難。學者們經過幾十年的研究，總結了匹配場處理(Matched-field processing, MFP)方法和匹配模處理(Matched-mode processing, MMP)方法是兩種可行的方法[1?2]。與MFP 相比，MMP 具有物理意義明確、計算量小和魯棒性好的優點，因此得到了更廣泛的應用[3?4]。因為利用垂直陣(Vertical line array, VLA)可以方便地計算模態深度函數，所以早期的探測設備以VLA 為主。Bogart 等[5]證明了如果水平陣(Horizontal line array, HLA)的孔徑足夠長，利用不同階模態的水平波數差異也可以分離模態，并提出了有效孔徑的概念。Premus 等[6]通過大孔徑水平陣提取低階模態的能量進行水面、水下聲源的分辨。李鵬等[7]和郭良浩等[8]學者對水平陣模態域波束形成進行了更深入的研究。

與固定式VLA 和HLA 相比，水下無人平臺(Unmanned underwater vehicle, UUV)搭載拖曳陣的探測方式具有靈活性高、隱蔽性好等優勢。Chouhan 等[9]利用多重信號分類(Multiple signal classfication, MUSIC)方法從拖曳陣數據中估計模態波數。黃勇等[10]利用合成孔徑方法進一步提高了波數分辨力，但由于不同階簡正波之間的相干性強，MUSIC方法在基陣運動距離大于模態相干距離時才能正確分離波數。Yang[11]利用聲壓和深度分離的格林函數之間的Hankel 變換關系，使用VLA接收數據進行聲場積分，準確估計了運動聲源波數譜。

和固定式探測設備相比，UUV 搭載的拖曳陣主要受到來自3 個方面的干擾。一是UUV 和感興趣目標之間動態變化的位置關系容易導致模型失配。二是UUV 自噪聲的干擾，由于UUV 自噪聲和感興趣的目標的輻射噪聲頻帶相近甚至重合，因此消除自噪聲的干擾具有重要意義。Candy 等[12]、Sullivan等[13]和Cederholm 等[14]許多學者研究了常規大型拖曳陣的載體自噪聲抑制問題，但大多數研究沒有指明如何選擇參考信號或參考信號很難獲取。Chi 等[15]在拖曳陣探測問題中研究了如何使用陣處理方法獲得參考信號。三是陣列瞬時隨機加速度擾動，由于UUV 容易受到海洋湍流和內波的影響，因此陣列存在明顯的瞬時隨機加速度擾動，在接收信號中引入了相位抖動。

針對上述存在的3 種干擾，本文提出了一種穩健的拖曳陣被動目標深度估計技術。首先在每個陣元上利用自適應濾波算法實現自適應噪聲抵消(Adaptive noise cancellation, ANC)，并通過二階鎖相環(Phase locked loop, DLL)濾除相位抖動，經過兩步抗干擾預處理得到了純凈的接收信號。然后對測量的聲場空間分布進行距離積分，計算模態估計的波數譜，聲場積分方法對陣列的運動形式沒有嚴格要求。最后從中提取模態能量并利用模態匹配器在不同深度進行匹配，估計出目標深度。

1 淺海簡正波模型

假設淺海環境為與距離無關的水平分層波導，目標聲源在深度zs以速度vs勻速水平直線運動，UUV 在深度zr以速度vr勻速水平直線運動，聲源和UUV 的速度矢量與兩者位置連線的夾角分別為θs和θr，聲源輻射頻率為Ω。根據文獻[16]，以基陣為參考系的接收信號表達式為

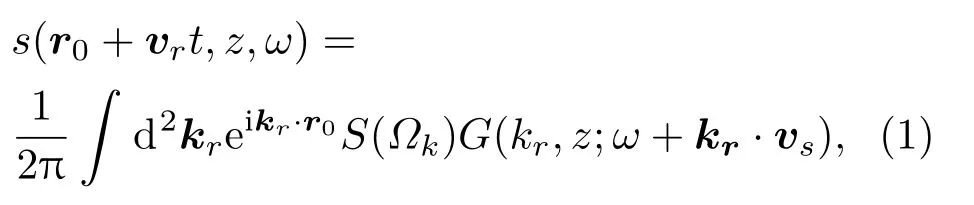
其中，kr是水平波數矢量，G(kr,z;ω+kr ·vs)是頻率為ω+kr ·vs的深度分離的格林函數，S(Ωk)是聲源功率譜，Ωk是包含多普勒頻移的聲源頻率，Ωk=ω-kr ·(vs-vr)。實際探測時，聲源到基陣的距離一般遠大于探測基陣孔徑，因此，為了簡化計算，可以近似認為θs和θr保持不變。利用Hankel變換代替水平波數的二維Fourier變換，再將格林函數表示為具有離散水平波數的模態累加的形式，可以得到簡正波模型下的接收信號表達式為

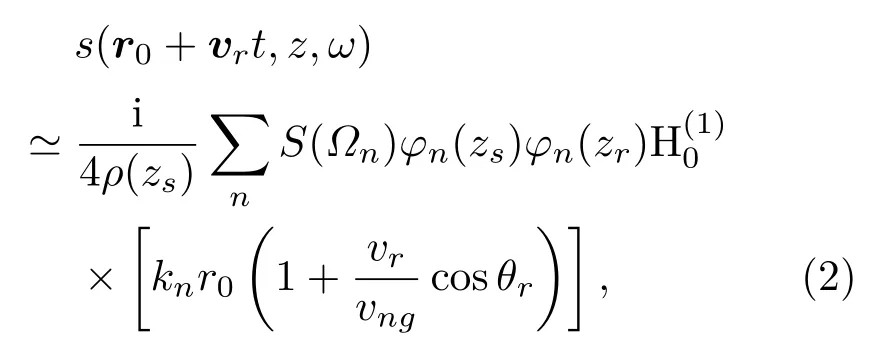
其中，Ωn=ω -kn(vscosθs -vrcosθr)=ω[1-(vs/vnp)cosθs+ (vr/vnp)cosθr]，vng和vnp分別是第n階模態的群速度和相速度，kn是Sturm-Liouville 本征方程在確定邊界條件下的解，表示離散的水平波數，φn(z)是對應的本征函數。

2 確定運動狀態下的目標深度估計

本節針對運動狀態確定的陣列提出基于被動合成孔徑的目標深度估計算法，解決未知隨機加速度擾動和自噪聲干擾的預處理算法在第3 節提出。由于簡正波不同模態的水平波數差異小，而且拖曳陣物理實孔徑有限，因此需要利用UUV 的機動能力，對目標信號進行持續觀測以獲得足夠的空間增益。已經有一些學者使用被動合成孔徑方法以提升模態估計精度[11]。使用傳統被動合成孔徑方法能夠形成虛擬陣元的大孔徑，當拖曳陣非勻速直線運動時需要設計復雜的相位補償算法，甚至可能失效。本節采用的聲場積分方法也是一種合成孔徑方法，但與前述方法不同的是，首先通過陣處理在每個測量位置獨立計算聲壓，然后對其進行距離積分獲得空間增益，最后進行模態匹配得到目標深度估計結果。由于不需要先合成虛擬孔徑再進行參數估計，因此陣列可以以任意運動形式進行探測，保證了算法的穩健性。

2.1 聲場積分法模態估計

首先假設已得到不存在自噪聲和陣列瞬時隨機加速度擾動的陣列接收信號，將基于淺海簡正波模型的信號表達式(2)轉換到時域。為后續表述方便，假設目標位于拖曳陣艉部端射方向，即θr= 180?，拖曳陣陣元數為M，以d為陣元間隔均勻分布，拖曳陣遠離目標一端的陣元為參考陣元，探測開始時，參考陣元和第m個陣元與聲源的距離分別為r0和rm=r0-(m-1)d。根據第1 節的分析，當聲源輻射頻率為f0的單頻信號時，UUV 接收到一串經過多普勒頻移的離散頻點信號，對應的各階簡正波頻率為ωn= 2πf0+kn(vs-vr)，因此第m個陣元的時域信號為

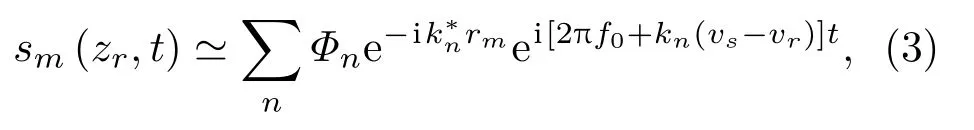
為了恢復聲場空間分布p(r,zr)，首先將陣元接收信號劃分為長度相同的一系列數據塊，數據塊總數為Q，每個數據塊持續時間為T，包含L個采樣點，T=L?t，其中?t是信號采樣間隔，用tq,l=qT+l?t表示第q個數據塊中第l個采樣點對應的時間，陣列在數據塊持續期間的位移量為R，可以將式(3)轉換為

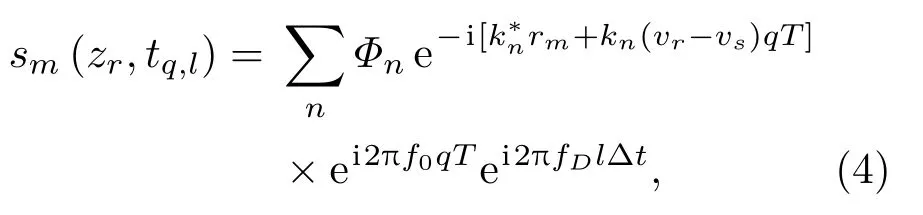
其中，fD=f0[1-(vr-vs)/c]是多普勒頻移后的接收信號頻率。對每一個數據塊進行Fourier 變換可以得到

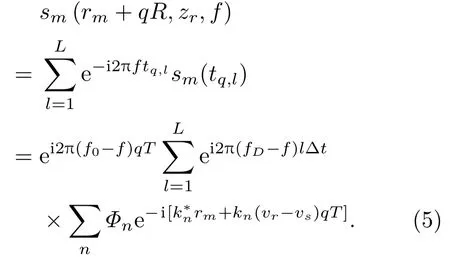
根據式(5)，聲壓的空間分布可以通過每一個數據塊的在f=fD的Fourier 變換結果乘以e?i2π(f0?fD)qT得到估計，即

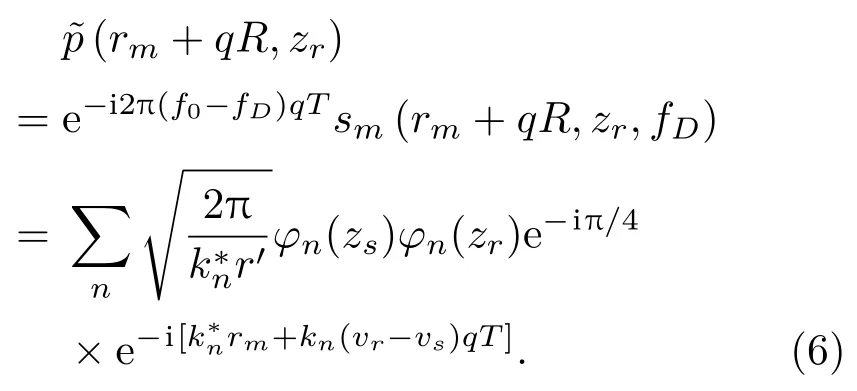
觀察式(6)容易發現，動態聲場中的聲壓分布與聲源靜止時情況有兩點不同。首先，指數函數中的速度差表明，由于聲源運動，陣列在第q個采樣區間的測量聲壓的位置到聲源的實際距離為(vr-vs)qT，而非陣列的空間位移qR。此外，指數函數中的k?nrm表明，空間各處不同階簡正波之間的固有相位差受初始距離和陣列速度共同影響。

在與距離無關的水平分層環境中，窄帶聲源的聲壓p(r,zr)和深度分離的格林函數g(kr,zr)之間構成Hankel 變換關系，如果滿足遠場條件，則可以用Fourier變換進行近似，即

其中，S(r′)是用于補償能量衰減的加權系數，比較式(6)與式(7)可以發現，可以在式(7)的離散形式基礎上稍加修改得到深度分離格林函數的估計值，也就是模態波數譜，如下所示：

其中，S(q)是和S(r′)對應的離散形式的加權系數，可以根據每個數據塊的信號能量的倒數計算得到。Am= eikrmd是模態域導向向量的第m個分量，通過計算陣元聲壓的加權和獲得了模態域的陣增益。將式(6)代入式(8)不難發現，估計的模態波數譜(kr,zr)和模態深度函數之間的關系為

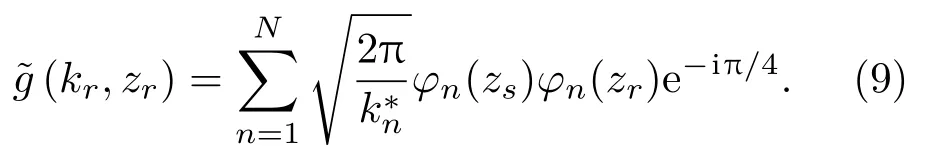
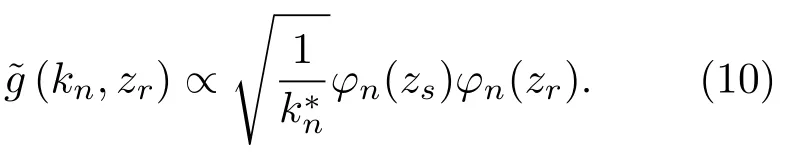
以上的分析假設陣列和目標都處于勻速直線運動狀態，當陣列速度變化時，只需要針對每個數據塊獨立計算聲壓，然后根據UUV 記錄的速度計算每個測量位置對應的和目標的相對距離，最后代入聲場積分式中即可。在仿真中將做進一步分析。

2.2 模態匹配

在得到接收信號的波數譜后，可以采用模態匹配的方法估計目標深度，模態匹配器結構為Camberra 距離的負指數：

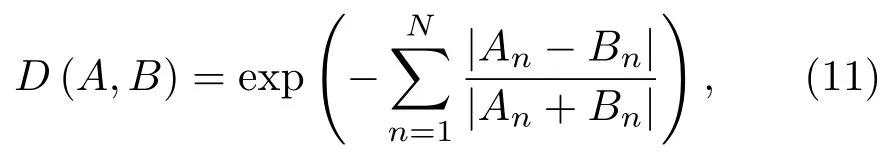
其中，A和B分別是估計的歸一化模態能量和根據已知環境信息仿真的歸一化模態能量，An和Bn分別是其第n階模態對應的能量。在對環境信息進行測量以后可以使用Kraken 軟件仿真各階模態的水平波數和模態深度函數。結合仿真的波數信息可以從2.1 節計算的模態估計波數譜中提取模態能量，即在仿真波數附近搜索波數譜峰值。由于不同階模態的能量一般差異較大，如果采用傳統的歐式距離進行度量，不能反映模態能量變化和起伏帶來的影響，因此采用式(11)定義的Camberra 距離的負指數來度量模態匹配度，Camberra 距離是經過尺度調整的差的絕對值之和，在分母中引入估計值和仿真值的和，可以將絕對能量偏差轉化為考慮了模態能量起伏的相對偏差。通過計算其負指數可以將模態匹配度映射到[0,1]。將假想目標深度從海面到海底進行遍歷，分別計算對應的模態匹配度，最大值對應深度就是估計的目標深度。

3 抗干擾預處理

第2節中推導的基礎是陣元接收信號不包含航行器自噪聲，同時也不受陣列瞬時隨機加速度擾動影響。然而在實際探測過程中，始終存在這兩部分干擾，因此需要對數據進行預處理。實驗數據顯示，拖曳陣接收的UUV自噪聲以300 Hz 以下的低頻線譜為主。這也符合噪聲產生的機理，因為UUV的螺旋槳轉速不足以產生空化，所以螺旋槳噪聲以和軸頻、葉頻相關的線譜為主，同時UUV在水下航行，所以不存在殼體與水面相互作用帶來的寬帶噪聲。設計自適應濾波器實現ANC，主要是考慮參考信號如何獲取以及選擇何種自適應算法。Chi 在文獻[15]中提出了一種解決問題的思路。

選擇濾波器長度的原則是保證其大于噪聲自相關時間和從航行器到每個陣元的聲傳播時延。本文研究的拖曳陣采樣率為10 kHz，從最遠端陣元到UUV 的距離dmax為50 m，典型淺海環境深度h不大于100 m。由于自噪聲頻率較低，波長長度與陣列空間結構相差不大，因此從UUV 到拖曳陣的傳播過程是一個復雜的近場問題，不適合用聲線的反射建模。盡管如此，用海面/海底反射路徑的時延作為信號時延的一個大致估計是合理的。假設聲速c=1500 m/s，從載體出發經一次海面/海底反射到最末端陣元的最大傳播時延τmax的計算公式為

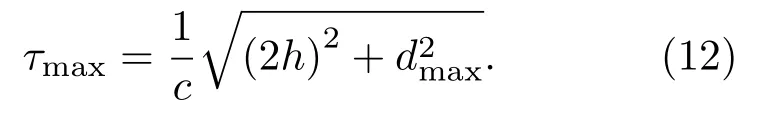
根據上述幾何結構計算，τmax<0.13 s。計算測量信號的自相關函數如圖1所示，容易發現當自相關時間大于0.2 s 時，信號相關性迅速減弱。綜合考慮傳播時延和自相關時間，濾波器長度應大于2000。

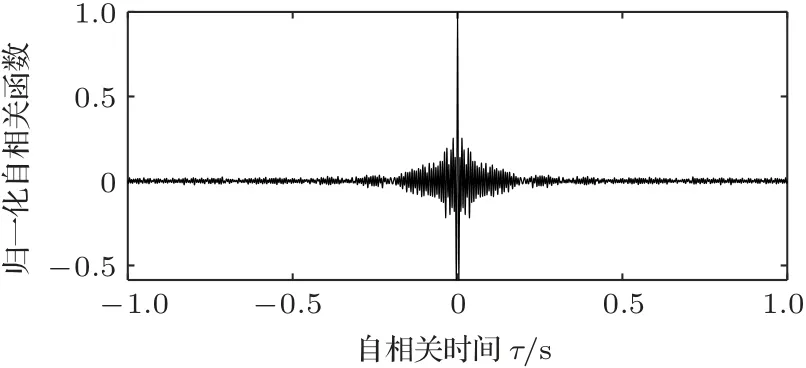
圖1 自噪聲自相關函數Fig.1 Autocorrelation function of the self-noise

在ANC 應用中，通常在噪聲源附近放置傳感器采集參考信號，然而在水下應用中，額外放置水聽器的方案會顯著增加設備復雜性，因此考慮利用波束形成方法直接從陣列接收信號中獲取參考信號。實驗過程表明，拖曳陣在工作狀態下近似平直且與UUV 在同一深度，因此可選擇陣列指向UUV 的方向計算各陣元時延，對陣元采集信號進行升采樣后反向時延疊加，再降采樣得到自適應濾波器的參考信號。

不同的自適應算法具有不同的計算復雜度和收斂特性，選擇算法的目的主要是在計算復雜度和收斂特性之間進行平衡。根據上述分析，在拖曳陣ANC 應用中陣元數較多，并且濾波器長度較長，因此應盡量減小計算復雜度以減輕處理器壓力。本文選擇頻域分塊最小均方(Frequency block adaptive least mean square, FBLMS)算法作為陣元數據預處理算法。FBLMS 算法借助快速Fourier變換(Fast Fourier transformation, FFT)實現快速卷積和快速相關運算，并且可以通過對頻域抽頭權向量使用獨立的歸一化步長參數，顯著提高算法的收斂速度，有關FBLMS 算法的更多內容可以參考文獻[17]，結合上文對濾波器長度的分析，本文的濾波器參數選取為濾波器長度2048，塊長度2048。

2.1 節中提出的聲場積分法可以在陣列非勻速運動，但確知運動形式時獲得測量數據的模態估計，實際應用中，陣列接收信號還由于受到未知的瞬時隨機加速度擾動而產生相位抖動，需要采用針對性預處理進行消除。二階鎖相環具有快速收斂的相位跟蹤性能，在水下聲通信中發揮著重要的作用[18?19]。在相位抖動抵消預處理中，首先對PLL的輸出相位進行平滑，然后從輸出相位中減去平滑后的相位可以得到相位抖動的估計，最后根據相位抖動估計對陣元數據進行補償。抗干擾算法的流程圖如圖2所示。

圖2 抗干擾算法流程圖Fig.2 The schematic of anti-interference algorithm

4 仿真實驗

仿真分為3個部分，首先在UUV非勻速運動的情況下將本文提出的方法與SA-SAMV方法進行比較，然后在受UUV 自噪聲干擾的情況下研究抗干擾算法帶來的穩健性提升，最后仿真目標頻率變化和合成孔徑距離的變化對目標深度估計的影響。

描述聲源和UUV 拖曳陣的運動狀態以及聲學環境參數的淺海波導模型如圖3所示，水深44 m。聲源頻率為145 Hz，深度為zs=23 m，向左水平速度為vs。拖曳陣陣元數為16，相鄰陣元間距為1 m，深度為zr= 11 m，向右水平速度為vr。聲源處于拖曳陣艉部端射方向，兩者背向運動，初始距離為2000 m。

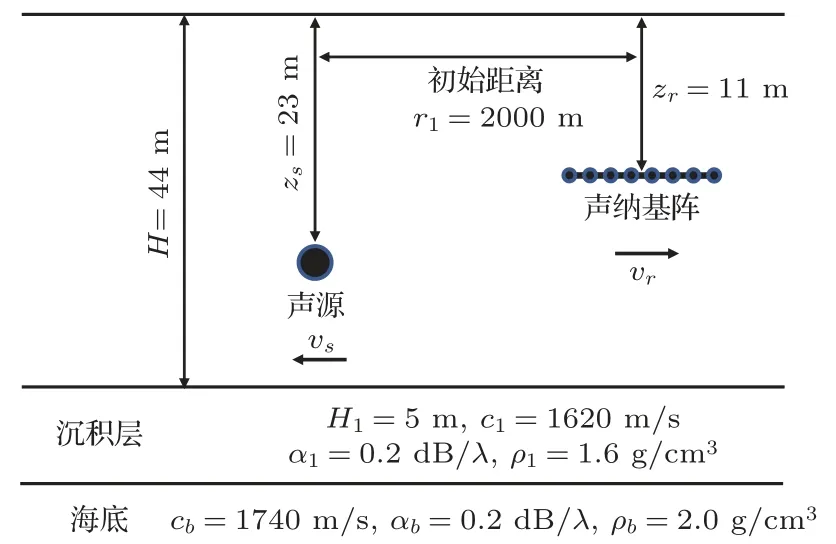
圖3 淺海波導模型Fig.3 The model of shallow sea waveguide

4.1 UUV非勻速運動仿真

選擇SA-SAMV 方法作為對比方法，它的原理是首先通過合成孔徑算法將運動小孔徑水平基陣擴展成虛擬的大孔徑水平基陣，然后利用稀疏近似最小方差準則估計簡正波模態能量，優勢是可以在較小的合成孔徑基礎上得到高分辨率模態估計，缺點是當陣列非勻速運動時表現不佳。在圖3所示的淺海環境中，假設聲源保持vs= 0.5 m/s 的速度勻速運動。拖曳陣先做勻加速運動再做勻減速運動，初速度vr= 2 m/s，勻加速階段的加速度為ar= 0.005 m/s2，持續200 s，勻減速階段的加速度為ar=-0.005 m/s2，持續200 s，探測時間總計400 s。根據運動關系，相對聲源的位移為1200 m。仿真陣列采樣率10 kHz。聲場積分法中的數據塊長度為4096，獨立處理每塊數據塊時以該時間段內的平均速度計算多普勒補償相位。SA-SAMV 方法使用全部測量數據進行目標深度估計，因此合成孔徑距離為1200 m。SA-SAMV方法和聲場積分方法的模態估計結果和目標深度估計結果分別如圖4和圖5所示。從圖4(a)中可以看出，在UUV 非勻速運動的情況下，SA-SAMV 方法的模態估計誤差很大，基本無法從中提取模態能量信息。從圖4(b)中可以看出，聲場積分法的模態估計結果保持了較好的分辨率。從圖5中可以看出SA-SAMV 方法的目標深度估計已經失效，而聲場積分方法的目標深度估計具有較高的穩健性。

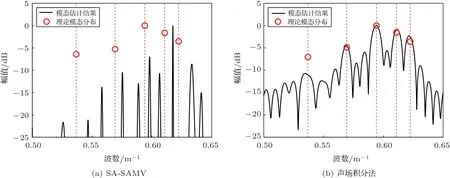
圖4 拖曳陣非勻速運動時的模態估計Fig.4 Modal estimation at unsteady speed

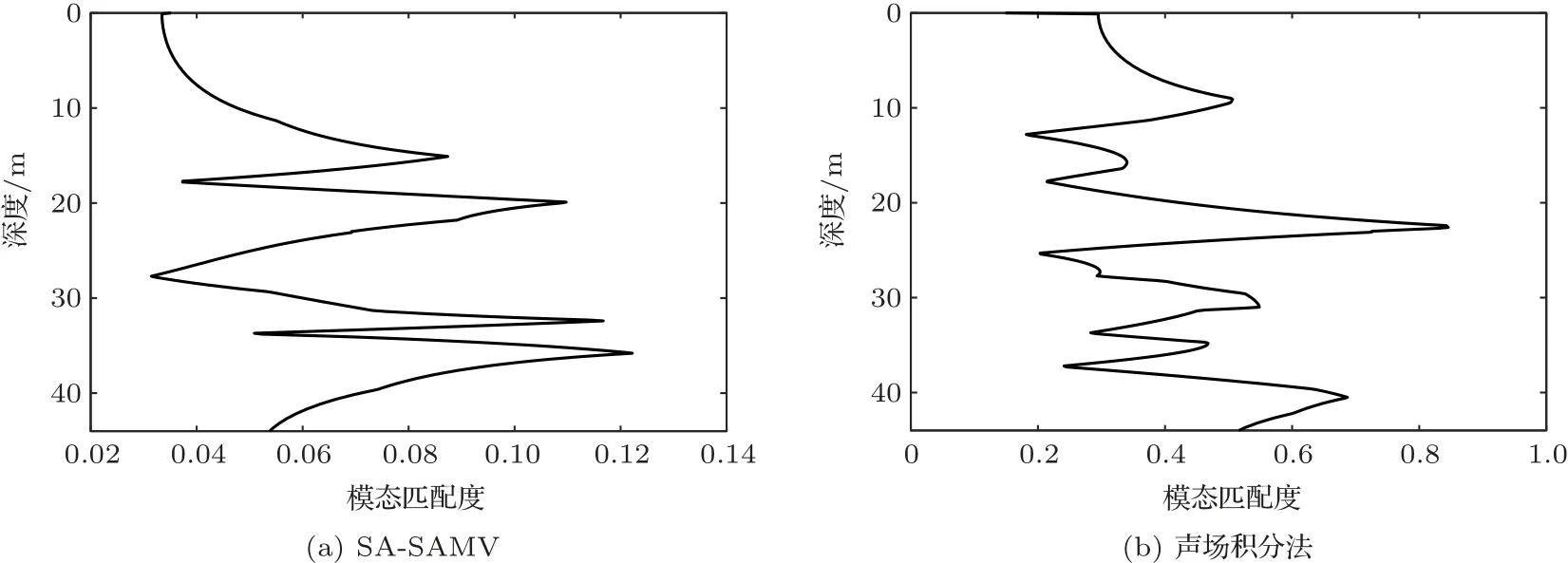
圖5 拖曳陣非勻速運動時的目標深度估計Fig.5 Target depth estimation at unsteady speed

4.2 拖曳陣ANC仿真

本節對UUV 拖曳陣ANC 進行仿真，相位抖動濾波的預處理將在實驗數據處理中進行研究。干擾信號是實驗中首陣元測量的自噪聲信號，并對其進行窄帶濾波，通帶頻率設置為[140 Hz, 160 Hz]。將濾波后的窄帶噪聲疊加到4.1 節無自噪聲干擾的仿真數據中，得到自噪聲干擾下的仿真接收信號，單通道功率譜如圖6所示。從圖6中可以看出，UUV自噪聲的中心頻率為152.5 Hz，與仿真的目標線譜接近，由于UUV自噪聲能量較強，因此在功率譜上，目標線譜已經不明顯。將經過抗干擾預處理的模態估計結果和深度估計結果與未經抗干擾預處理的結果進行對比，如圖7和圖8所示。通過對比可以看出，抗干擾預處理改善了波數譜和目標深度估計結果，但與無干擾情況下的模態估計結果相比，丟失了最高階模態。在實際應用中選擇模態匹配的模態階數時，通常只選擇低階模態，這是因為低階模態在波導中的傳播更加穩定，更加容易被識別；另外，高階模態對應的深度函數有較多的波腹和波節，在模態匹配時引入高階模態實際上降低了匹配算法的穩健性。圖8中的深度估計是選擇1～4 階模態的結果。

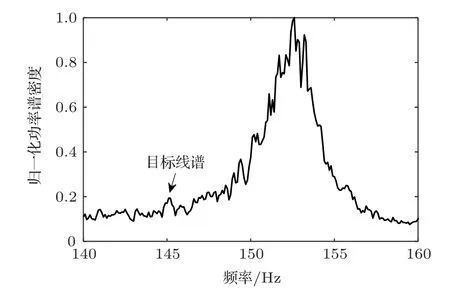
圖6 自噪聲干擾下仿真信號功率譜Fig.6 The power spectrum of simulated signal under self-noise interference

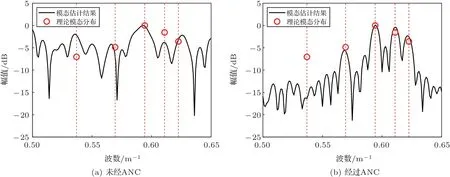
圖7 模態估計波數譜Fig.7 The estimated wavenumber spectrum with and without ANC

圖8 深度估計Fig.8 The target depth estimation with and without ANC

4.3 深度估計誤差的影響因素

為進一步研究目標深度估計誤差的影響因素，假設準確測量了環境信息，在4.2 節中的自噪聲干擾下使用聲場積分方法進行目標深度估計。聲源頻率為145 Hz 和245 Hz，以自噪聲作為干擾源定義的信干比變化范圍為-20～20 dB，合成孔徑距離為1000 m，通過100 次Monte Carlo 仿真得到經過ANC和未經ANC的目標深度估計誤差如圖9所示，從圖9中可以看出，ANC 預處理可以顯著降低自噪聲干擾導致的目標深度估計誤差，如果不經過ANC預處理，當信干比低于0 dB時，誤差明顯增大，導致目標深度估計失效。經過ANC 預處理可以在更低信干比實現目標深度估計。在信干比固定為10 dB的情況下，合成孔徑距離變化范圍為200～1000 m，頻率為145 Hz、195 Hz和245 Hz，通過100次Monte Carlo 仿真得到的目標深度估計誤差如圖10所示。從圖10中可以看出，聲源頻率一定時，目標深度估計誤差隨合成孔徑的增加而減小，當合成孔徑距離足夠大時，目標深度估計誤差不再進一步隨合成孔徑的增加而減小；當合成孔徑和信干比一定時，目標深度估計誤差與聲源頻率有關，對低頻聲源的模態估計更準確，這是因為低頻聲源激發的簡正波階數較少，波數間隔較大，易于分辨和估計。在實際應用中往往存在多目標，根據探測到的目標相對陣列的方向，可以對不同方向的目標并行地計算其聲壓的空間分布。由于式(8)利用波數域陣處理獲得了陣增益，陣列的陣元數越多則陣增益越高，因此在計算某個方向的目標的模態估計波數譜時，來自非當前方向的其他目標的信號可以等效為波數域的噪聲。對多目標情況進行仿真，假設除端射方向有感興趣的水下目標外，在其他方向還有一個靜止的干擾目標，深度為5 m。改變干擾目標的方向和頻率，得到感興趣目標深度估計誤差隨波數域信噪比的變化如圖11所示。從圖11中可以看出，當干擾目標能量有限時，對感興趣目標的深度估計誤差影響較小。

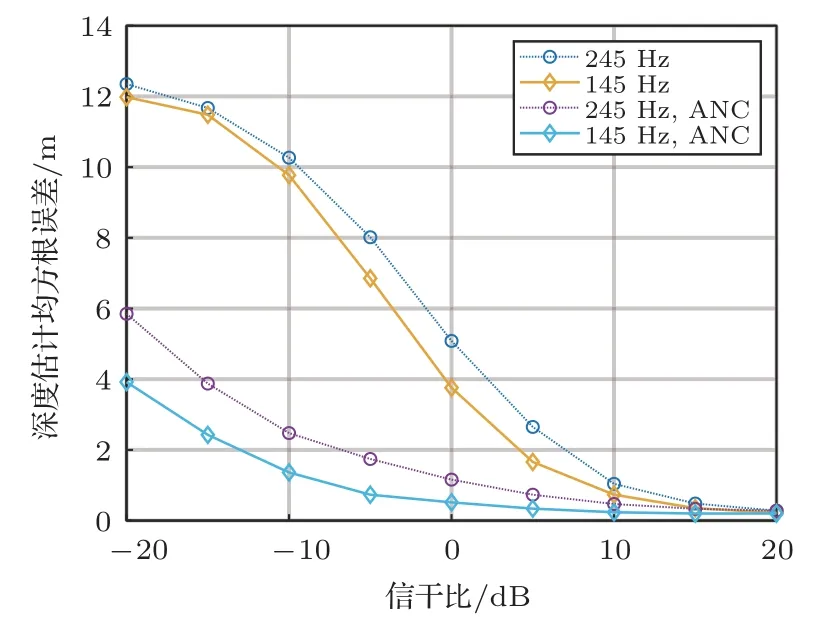
圖9 目標深度估計均方根誤差隨自噪聲能量變化Fig.9 The root-mean-square error of target depth estimation varies with the SIR defined by selfnoise

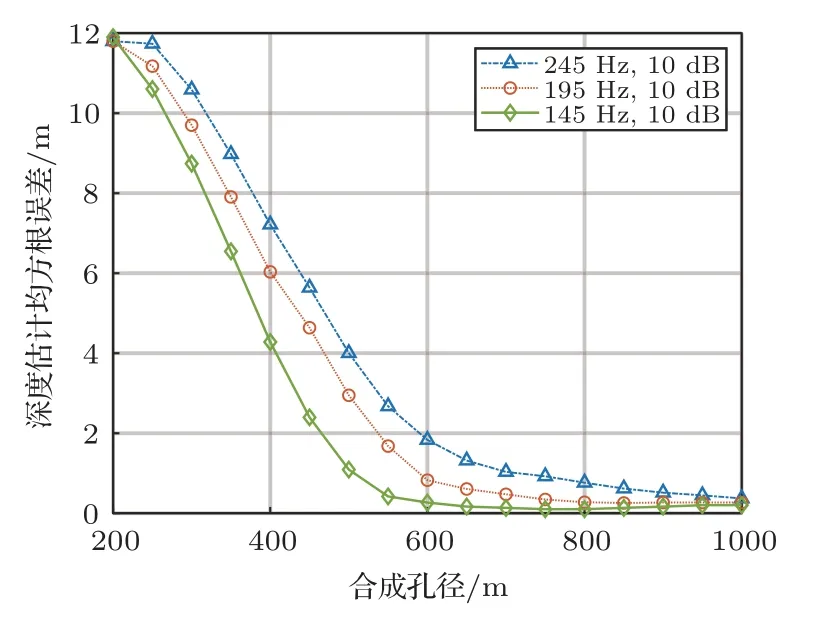
圖10 目標深度估計均方根誤差隨合成孔徑變化Fig.10 The root-mean-square error of target depth estimation varies with the synthetic aperture

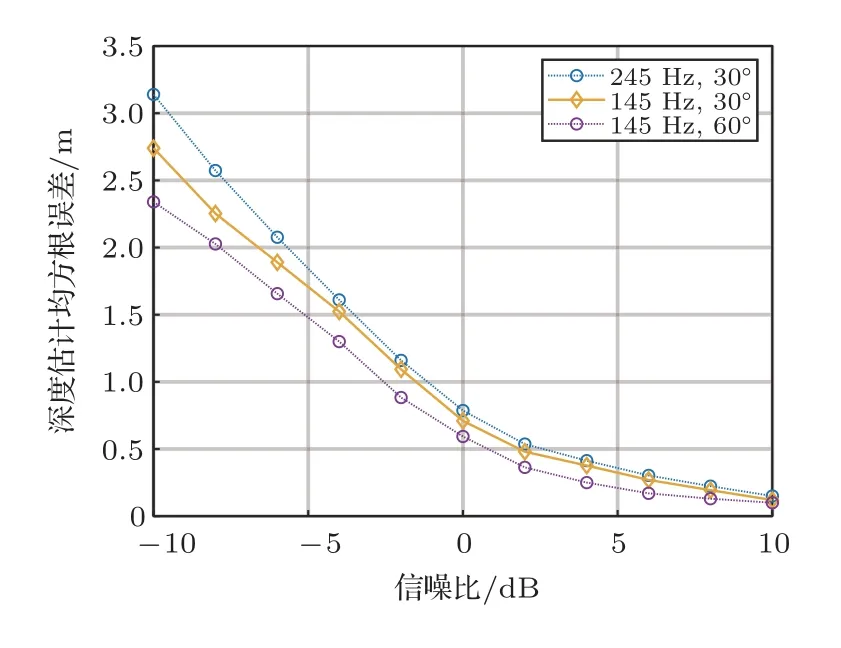
圖11 目標深度估計均方根誤差隨波數域信噪比變化Fig.11 The root-mean-square error of target depth estimation varies with the SNR in wavenumber domain

5 實驗數據處理

實驗在夏季進行，聲速剖面為強負梯度結構，如圖12所示。低頻聲源模擬目標信號頻率為165 Hz和195 Hz，聲源深度為25 m。拖曳陣陣元數為16，陣元間距為1 m，搭載著拖曳陣的UUV 以1.62 m/s的預設速度背向駛離聲源，拖曳陣深度為13 m，初始距離為750 m，數據采集時長為600 s，合成孔徑長度為972 m。

195 Hz 信號的相位跟蹤和相位抖動估計結果如圖13所示，從相位跟蹤圖中可以看出，實驗中UUV的速度不是恒定的，經歷了慢速-快速-慢速的變化過程；從相位抖動估計圖中可以看出，在實驗初始階段，運動狀態較穩定，從250 s 開始出現瞬時隨機加速度擾動，450 s 后的50 s 內干擾嚴重，和快速運動階段吻合。

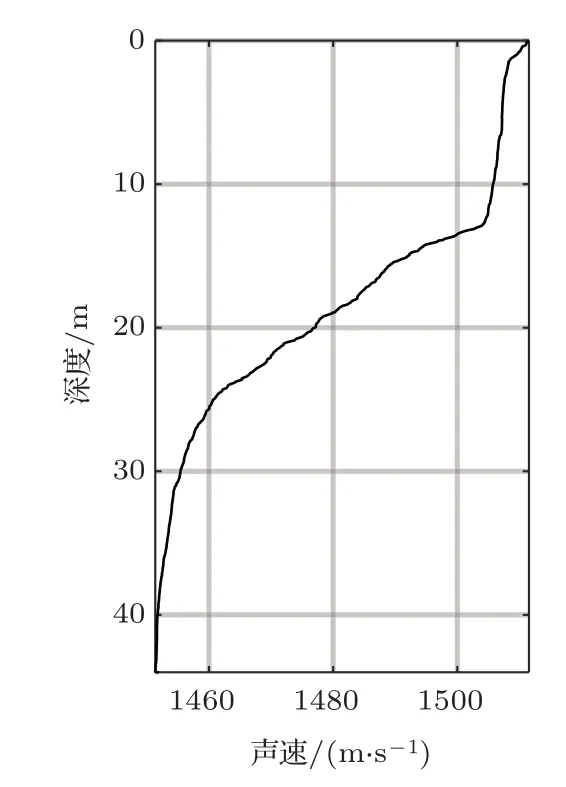
圖12 聲速剖面Fig.12 Sound speed profile

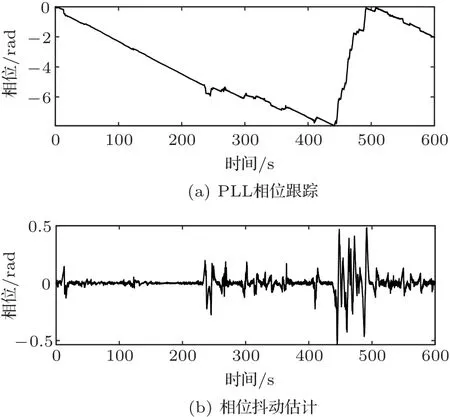
圖13 相位跟蹤和相位抖動估計Fig.13 Phase estimation and phase jitter estimation

使用SA-SAMV方法和本文提出的穩健方法進行對比，計算的模態估計結果和對應的深度估計結果如圖14所示。從圖14(a)中可以看出，由于本段數據采集過程中陣列存在明顯的速度變化，因此SA-SAMV方法計算的模態波數譜中出現若干偽峰，根據仿真的波數位置提取模態信息并計算的目標深度估計結果顯示在圖14(b)中，從中可以看出，目標深度匹配度最大值對應深度為30 m，而目標真實深度25 m處僅出現次極大值，目標深度估計存在5 m的誤差。

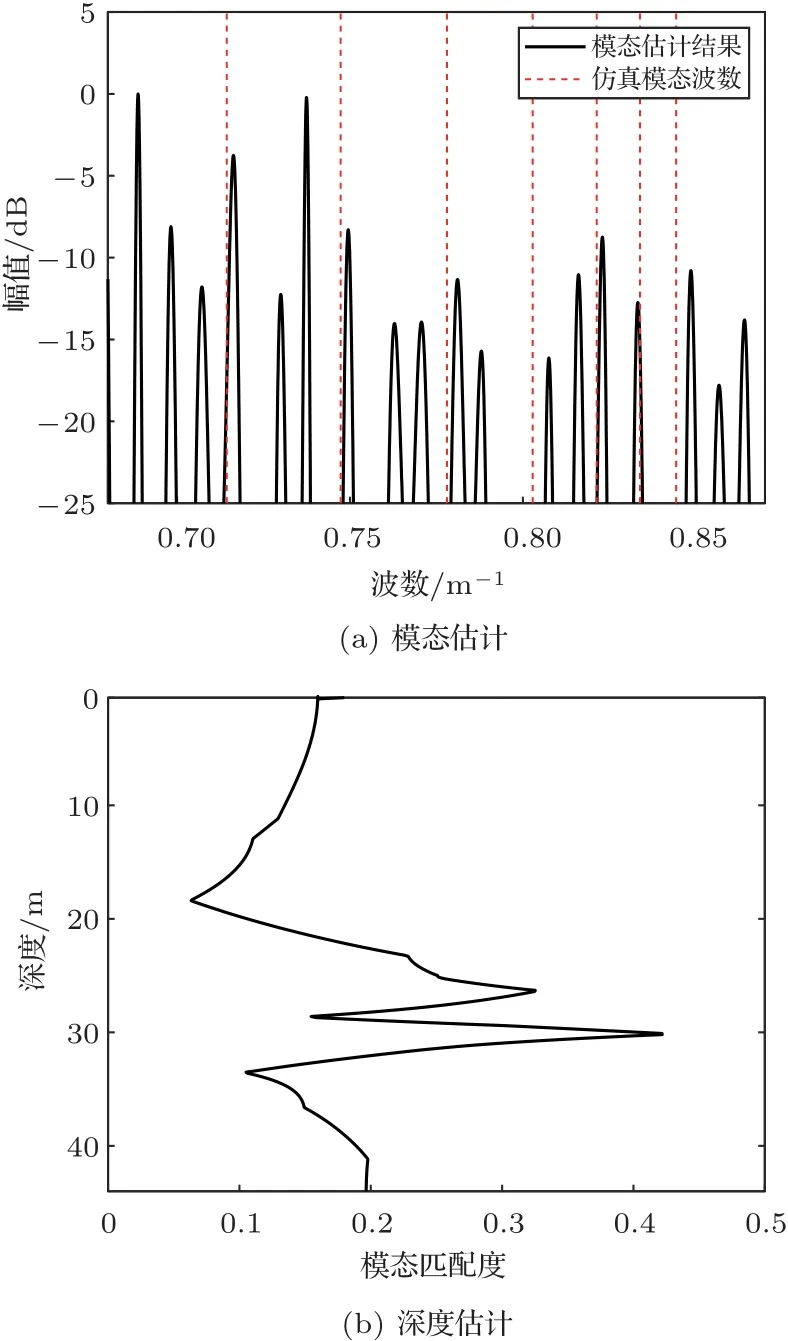
圖14 使用SAMV 方法獲得的195 Hz 信號的模態估計和深度估計Fig.14 The normalized modal estimation and the target depth estimation for 195 Hz using SASAMV

195 Hz 信號經過抗干擾預處理和未經抗干擾預處理的模態估計結果分別如圖15(a)和圖15(b)所示，其中紅色虛線為仿真模態波數。與之對應的目標深度估計結果如圖16所示。從圖15(b)中可以看出，由于未進行抗干擾預處理，在第二階和第三階模態處未能檢測到模態峰值，而在圖15(a)中有相對明顯的模態能量。從圖16(a)中可以看出，經過抗干擾預處理的目標深度估計在25 m 處出現峰值，與真實聲源深度吻合，證明了深度估計算法的有效性。在未經抗干擾預處理的圖16(b)中，目標深度估計結果準確度下降，具體表現為真實目標深度處峰值不尖銳，且在近水底深度處有較強偽峰。從圖15(a)中還可以看出，模態估計波數譜中的峰值位置與理論值并非完全吻合，這是因為實驗中無法做到精確測量環境信息，因此仿真的波數位置與實際波數位置存在偏差。在實際應用中，需要在仿真得到的波數位置附近選取距離仿真波數距離較近的峰值進行匹配。另外，模態匹配時階數選擇是一個需要考慮的問題，增加模態匹配的階數，可以在一定程度上提高目標深度估計分辨率，但同時也降低了估計結果的穩健性，當測量的環境信息與真實環境偏差大時，這種穩健性的下降會帶來嚴重的誤差問題。從另一個角度來看，實際上通常對水下目標進行深度估計時，分辨率并不是最主要考慮的性能，因此實際應用中傾向于選擇較少階數的模態進行匹配。

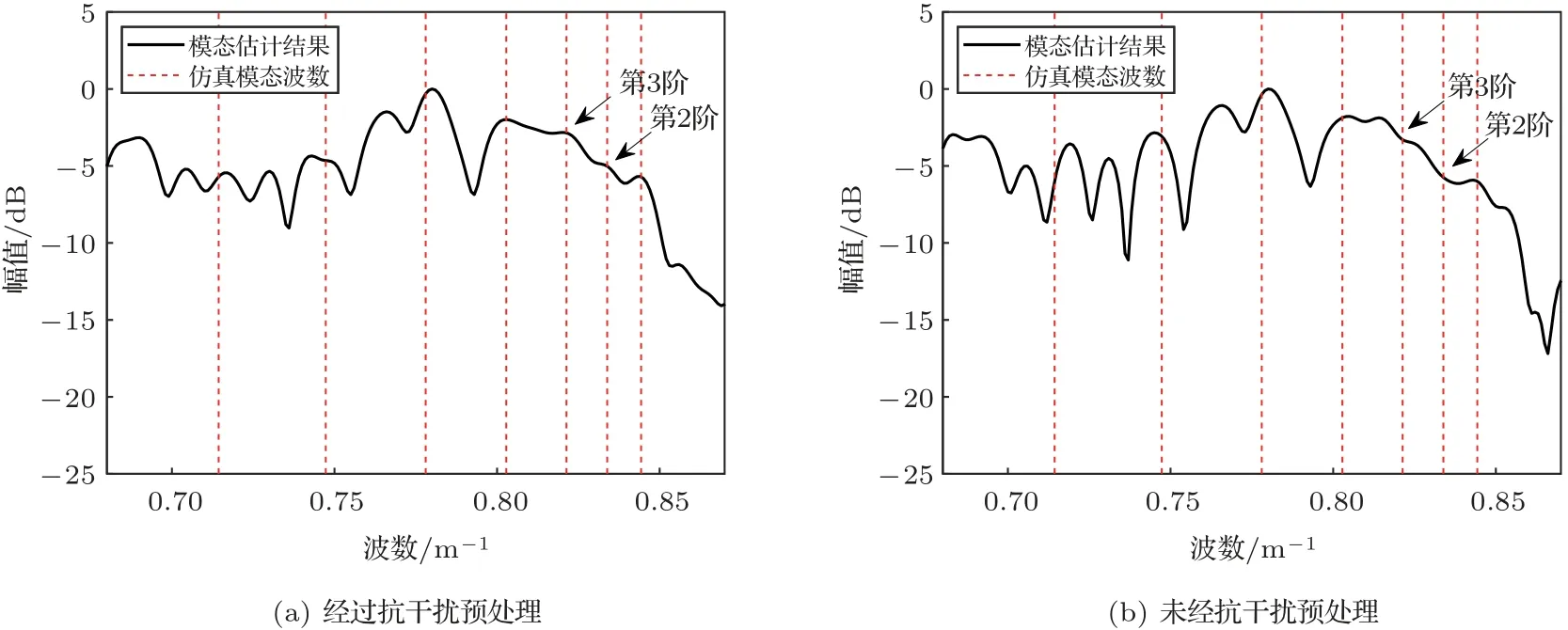
圖15 195 Hz 信號的模態估計Fig.15 The normalized modal estimation for 195 Hz tonal signal

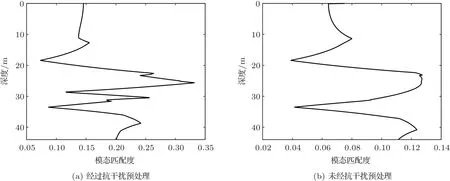
圖16 195 Hz 信號的深度估計Fig.16 The target depth estimation for 195 Hz tonal signal

6 結論

本文利用淺海動態聲場的傳播規律，在簡正波模型的基礎上提出了一種UUV 拖曳陣被動合成孔徑目標深度穩健估計方法，通過基陣的運動獲得聲場測量的空間增益，在預處理階段使用FBLMS 算法消除UUV 自噪聲干擾，使用二階鎖相環消除陣列隨機瞬時加速度干擾。仿真表明，該方法在復雜運動場景下和存在上述兩種干擾的環境中的穩健性優于傳統方法，聲源頻率、合成孔徑距離和信干比決定了深度估計誤差。但在穩健性提升的同時，模態估計的分辨率相比SAMV方法有所下降，需要更大的合成孔徑分離模態。最后利用實驗數據驗證了該方法對水下低頻線譜聲源的深度估計能力。在后續工作中，將進一步研究模態匹配的階數選擇問題和寬帶噪聲目標的深度估計問題。