四邊簡支含多孔材料雙層板隔聲特性?

陳 亮 沈 敏

0 引言

由于采用單一的材料進行噪聲控制效果并不理想，研究人員對多種材料進行組合設計復合板結構，提高板結構隔聲特性[1?2]。在兩層平板中間填充多孔吸聲材料，在飛機艙室結構中非常普遍。深入探索雙層板結構聲振耦合系統的物理本質，可以更好地指導高速機車、艦船、飛機、航天飛行器等的聲學優化設計[3]。

目前，針對復合板結構隔聲特性已有許多相關的研究，總體可分為無限大板和有限大板結構兩類。對于無限大含多孔材料復合板結構聲振耦合特性，Bolton 等[4]建立了多孔材料與面板的耦合邊界條件，理論研究了在雙層板中夾層為多孔彈性材料的隔聲特性。Liu[5]在Bolton等研究的基礎上，研究了含多孔材料的無限大三層板結構的隔聲特性。Zhou等[6]考慮了外流場對傳聲損失的影響。陳衛松等[7]通過傳遞矩陣法研究了芯層為多孔材料的三層復合板結構隔聲特性。Lee 等[8]將板中間的多孔材料作為等效流體，簡化了理論模型，計算了雙層板結構隔聲量(Sound transmission loss,STL)。Yablonik[9]基于聲傳遞理論計算雙層鋁板中含有多孔材料的復合板STL，使用Johnson-Champoux-Allard 等效模型分析聲波在多孔材料中的傳播。

實際工程中大多為有限大復合板結構，應當考慮邊界條件對結構聲振特性的影響。Carneal 等[10]提出用結構模態疊加法表示聲場的分布，理論計算了四邊簡支雙層板的STL，并與實驗結果對比，驗證了其理論結果的正確性。Xin[11?12]等分別研究了簡支和固支支撐下中間為空氣芯層雙層板結構的隔聲特性，并討論了相關結構參數對系統隔聲特性的影響。Liu 等[13]研究了四邊固支邊界條件下，含多孔材料復合雙層板結構隔聲特性。

然而，對于其他邊界條件下，含多孔材料和空氣層的復合雙層板結構隔聲特性的分析尚未見到報道，對于其他邊界條件下復合板結構隔聲特性研究尚不充分。因此，本文旨在研究四邊簡支邊界條件下，中間芯層為多孔材料和空氣層的復合雙層板結構的隔聲特性。首先基于流體飽和多孔彈性介質的聲傳播理論(Biot)計算聲波在多孔介質中的傳播波數；繼而采用四邊簡支邊界條件下板結構的模態函數，利用模態疊加法和伽遼金(Galerkin)法推導復合板結構隔聲系數理論模型，并數值求解復合板結構STL。將理論模型得到的四邊簡支復合板STL與實驗結果對比，驗證理論模型的正確性。最后，詳細討論四邊簡支邊界條件、板結構尺寸和多孔材料主要參數對隔聲特性的影響。

1 雙層板內襯多孔彈性材料聲學模型

1.1 四邊簡支雙層復合板聲學模型

雙層板由兩個各向同性、均質的薄鋁板作為面板，中間芯層是彈性多孔材料疊加空氣層組成。兩個鋁板四邊為簡支邊界條件，固定在無限大的剛性聲障上。平面簡諧波以俯仰角?和方位角θ斜入射到上層面板，如圖1所示。上面板的振動通過彈性多孔介質與空氣層作用向下傳遞，引起下面板振動并向外輻射聲波。假設由無限大剛性聲障隔開的入射聲場和透射聲場是半無限大的，具有相同的空氣密度ρ0、聲速c0。結構的尺寸如下：上板和下板具有相同的長寬a和b，上下板的厚度分別是h1和h2，芯層材料總厚度為H。

圖1 四邊簡支內襯彈性多孔材料雙層板結構Fig.1 A simply supported double-wall sandwich panel lined with poroelastic materials

雙層板中間內襯彈性多孔芯層材料或者空氣層可以組合成不同的結構，如圖2所示。圖2中顯示的結構AA是指兩塊面板中間只有空氣層；結構BB指的是兩塊面板都與多孔材料芯層直接綁定在一起；結構BU是第一塊板與多孔材料固定，第二塊板與多孔材料分離，通過空氣層耦合；結構UU是兩塊面板均與多孔材料分離，通過空氣層進行耦合。

圖2 雙層復合板不同結構Fig.2 Different configurations of the double-wall sandwich panel

1.2 聲波在多孔彈性材料中傳播

在給定的入射方向(?,θ)下，平面波入射到上面板，進入多孔彈性介質傳播，波數分量為

其中，空氣中入射的平面波波數k0=ω/c0。

根據Biot 的理論[14?15]，聲波在均勻且各向同性的流體飽和多孔彈性介質中傳播時，以快縱波、慢縱波和剪切波3 種形式傳播。由于接下來的分析中只討論了聲波垂直入射的情況，所以剪切波的影響可以忽視。k1、k2分別為快縱波、慢縱波的波數，具體表達式可參考Biot[14?15]。

利用固相-流體相的體積應變可以推導出位移分量的表達式，固相和流體相中位移在z方向分量表示為

固相和流體相在z方向的應力為

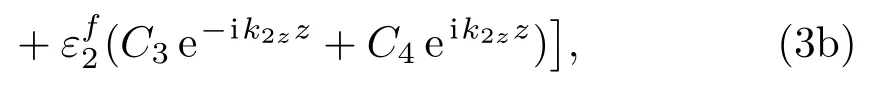
其中：k21,2z=k21,2-(k2x+k2y)為波數在z方向的分量，εs1、εf1、εs2、εf2為與材料參數相關的系數，可參考文獻[13]。將在多孔材料固相和流體相中的位移分量usz和ufz、應力σsz和σfz代入復合板結構中多孔材料與面板或者空氣層不同耦合界面邊界條件求解未知常數C1～C4。

1.3 耦合邊界條件

邊界條件取決于板和多孔材料的耦合關系，如圖3所示。假定面板是各向同性的均勻板，板的厚度對比板的橫向尺寸足夠薄，根據Kirchhoff-Love 板理論，面內變形以及剪切應力可以忽略。

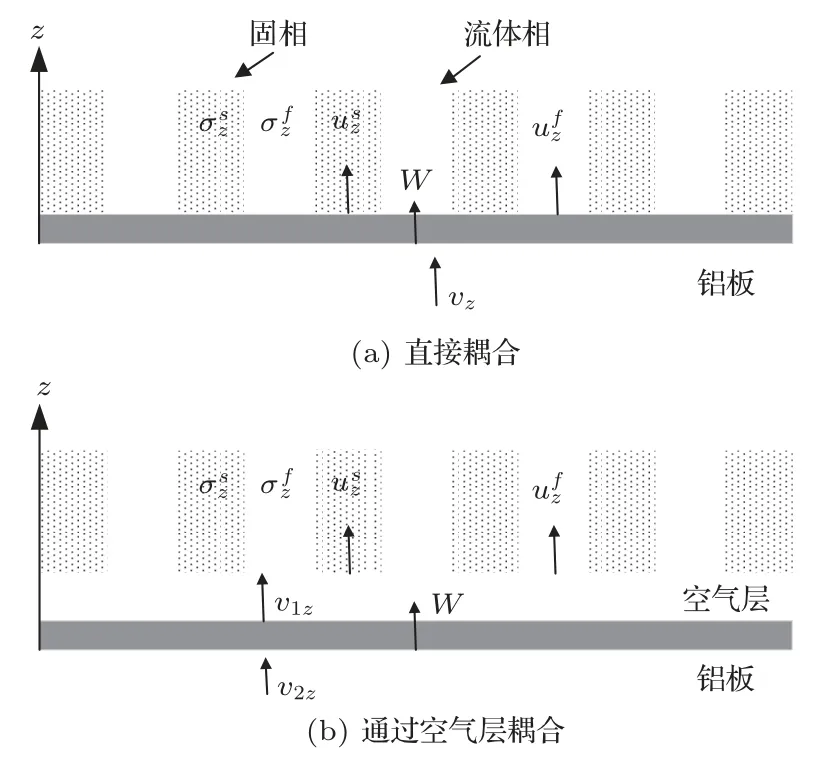
圖3 不同耦合情況Fig.3 Different coupling methods

板與多孔材料直接耦合如圖3(a)所示，必須滿足3 個邊界條件：一個法相應力條件和兩個法相位移條件：

多孔材料通過空氣層與板耦合如圖3(b)所示，在多孔材料表面有3 個邊界條件：兩個法向應力條件和一個法向速度條件：

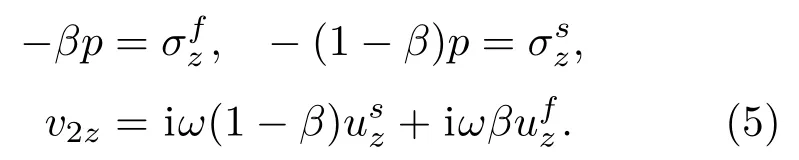
在兩層彈性板的表面有兩個邊界條件：兩個法向速度條件：

2 復合板BB布局聲振模型

本節詳細推導了BB結構的聲振問題，由于BU結構、UU 結構推導與BB 結構推導相似，本文將不再贅述。因為是彈性多孔材料直接與面板連接，所以芯層的厚度就是彈性多孔材料的厚度。

2.1 板的彎曲振動

用W1和W2分別表示上板和下板的橫向位移。在諧波激勵下，上下板的橫向變形可以用模態分解形式表達為

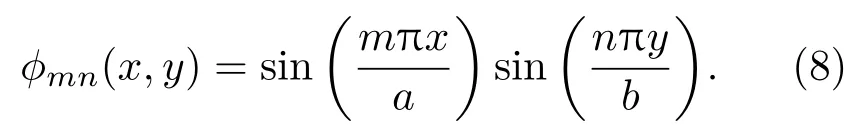
對于BB 結構，當兩塊板都直接與多孔材料固定，上下板的彎曲運動表達式為

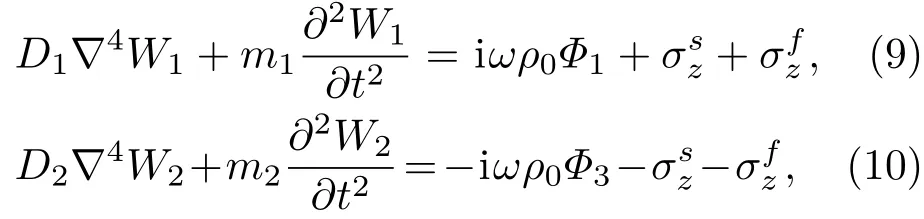
其中，雙調和算子?4= (?2/?x2+?2/?y2)2；板的面密度mi=ρphi(i= 1,2)，ρp為板的密度；彎曲剛度，Ep為板的楊氏模量，ηp為板的損失因數，νp為板的泊松比。

2.2 加權余量法

基于權函數的加權余量法，微分方程的解是形函數的線性組合，在整個域內，權函數與微分方程的乘積的積分可以設為0，權函數取形函數?mn。對式(9)和式(10)運用加權余量法可得

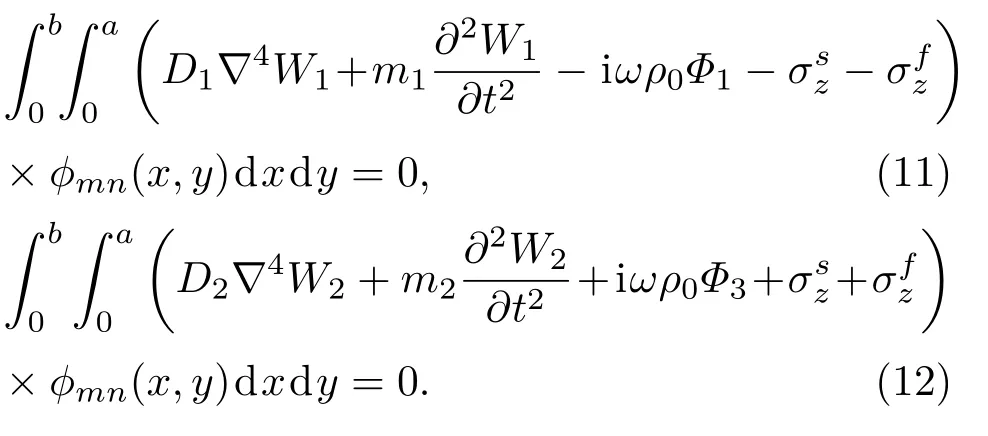
通過求解積分方程(11)和積分方程(12)，可以得

到

其中，矩陣(13)中的元素分別為

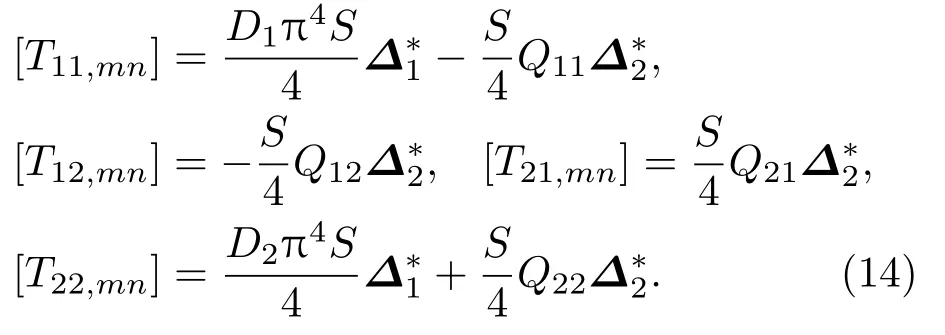
方程(11)和方程(12)中只有α1,mn和α2,mn是未知的，m、n取值是無限多的，但是這類方程可用截斷方法來進行數值求解：1 ≤m,n≤M，其中最大整數M取值需要同時保證精度高而且計算量小。M2×M2的矩陣??1和??2具體值在附錄A中給出。通過求解方程(13)可以計算出模態系數αi,mn(i=1,2)，從而能求解出板位移W1和W2。

2.3 復合板結構入射聲功率傳輸損失

入射聲場中的聲速度勢由一個入射波與一個反射波組成，其幅值分別為I和R，聲速度勢可表示為

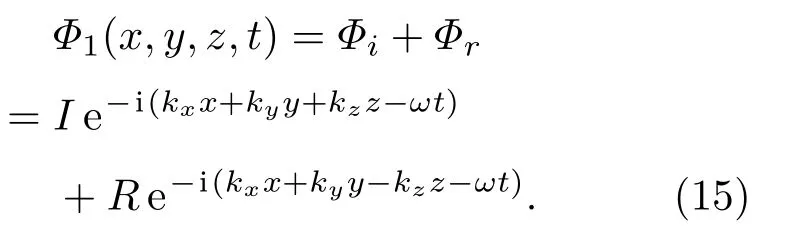
假設入射波是單位振幅，即I= 1，同時假設聲波透射場是半無限大且消聲終止，因此在這個聲場中就只有一個振幅為T的透射波，其聲速度勢可以表示為

將聲波入射速度勢帶入面板和多孔材料以及空氣層耦合的邊界條件可以分別求出反射系數R和透射系數T的表達式，通過加權余量法求解上板和下板的位移，可以得到反射系數R和透射系數T的具體數值。

聲功率定義為其中，質點速度與聲壓p的關系為v=p/ρ0c0，上標“*”表示共軛復數。

聲波的隔聲系數為輻射聲功率與入射聲功率的比值：

STL定義為：

3 結果與討論

本節討論四邊簡支約束雙層復合板隔聲特性。考慮到聲波垂直入射時，對于四邊簡支邊界條件，可以忽略剪切波的影響，因此，本文僅考慮聲波垂直入射下的情況。上下層面板都是鋁板，具體參數如表1所示。中間芯層是聚氨酯泡沫多孔材料，詳細參數如表2所示。復合板結構可形成4 種不同布局，除特殊聲明外，不同布局的芯層材料厚度分布如表3所示。空氣密度ρ0= 1.12 kg/m3， 聲速c0= 343 m/s，比熱比γ= 1.4，普朗特常數Pr=0.71。除特別聲明，板尺寸為0.3 m×0.3 m。

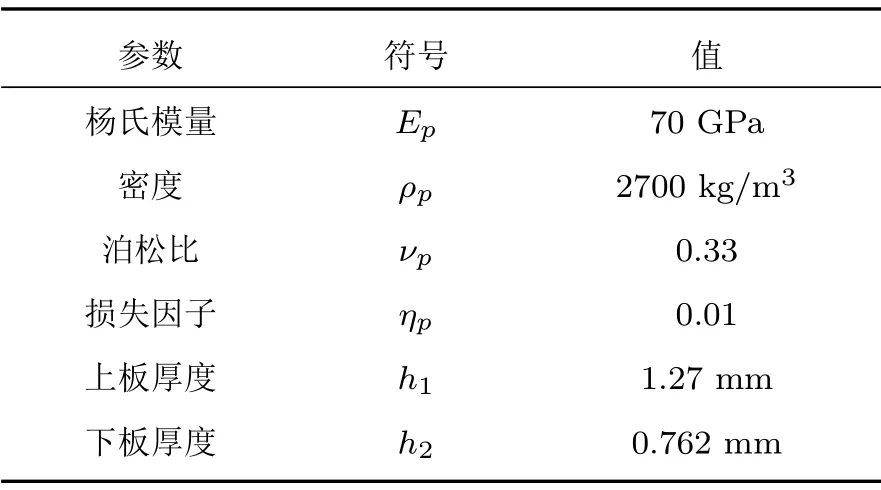
表1 鋁板性能參數Table 1 Property parameters of the aluminium plates

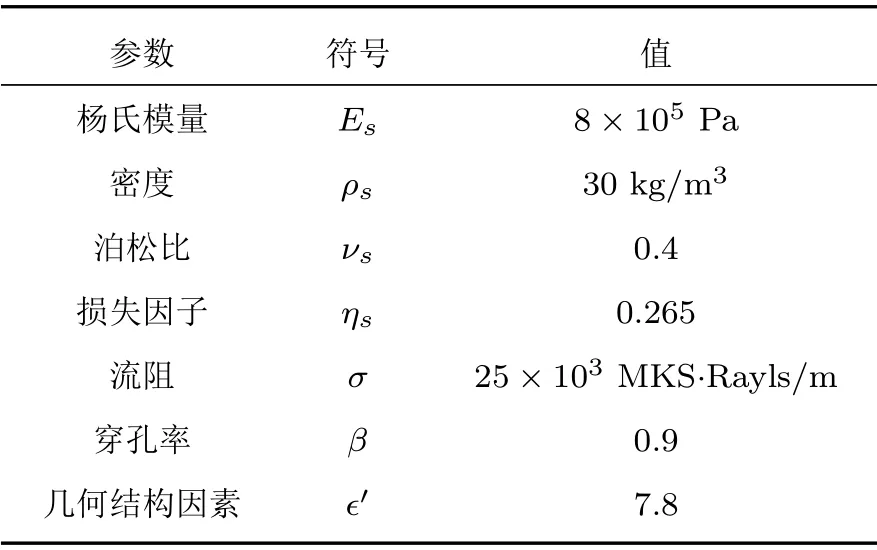
表2 彈性多孔材料性能參數Table 2 Property parameters of the poroelastic material

表3 AA、BB、BU、UU 結構各層厚度Table 3 Layers’ thickness of the AA, BB,BU, UU configurations

3.1 數值結果收斂性檢驗

由于理論結果是以級數形式出現的，需選取足夠的項數保證收斂。通常認為一旦一定項數的級數求和結果在給定的頻率下收斂，則該項數的級數求和結果在此頻率以下都能收斂[13]。在本次工作中頻率10 kHz 用作檢驗收斂性的最高頻率，如圖4所示。從圖4中可以看出，求解2M2×2M2的矩陣需要級數項數為25，總共1250項結果能收斂。

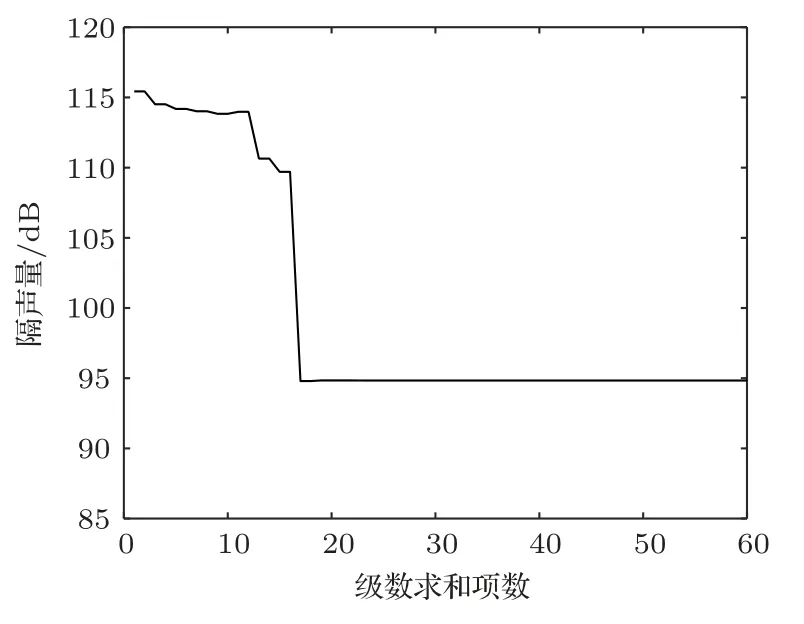
圖4 在10 kHz 垂直入射聲波激勵下，UU 結構傳聲損失級數解收斂性檢驗Fig.4 Convergence of double Fourier series solution for STL of UU configuration under the excitation of a normally incident sound at 10 kHz

3.2 模型可行性分析

若將UU 結構中多孔材料厚度設置為0 或者穿孔率設置為1，則UU 結構簡化成為AA 結構，即“ 板+空氣+板”。鋁板尺寸為a= 0.38 m,b= 0.3 m，厚度為h1=h2= 1.6 mm，空氣層厚度為H= 48 mm。通過前文推導的理論模型計算得到四邊簡支AA結構的STL，如圖5所示。

圖5中顯示了本文理論模型計算得到的STL、Carneal等[10]的實驗結果、Xin等[12]的理論模型計算得到的AA 結構STL。從圖5中可以看到，本文理論模型得到的STL 與Xin 等的理論模型得到的結果、Carneal 等的實驗結果都取得了較好的一致性。因為Carneal 等的實驗是在固支邊界條件下進行的，所以將理論中簡支邊界條件下板的剛度增加了倍來仿真四邊固支的邊界條件。為保持一致性，本文做同樣處理。

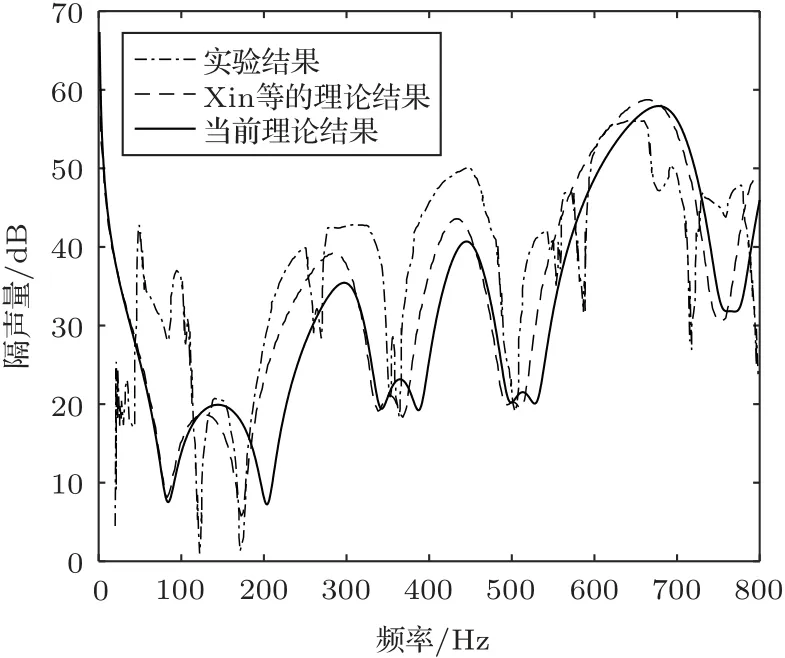
圖5 聲波垂直入射下傳聲損失的理論與實驗對比Fig.5 Comparison of STL between the current study and experiment under normal incidence

3.3 簡支邊界條件和固支邊界條件對復合板結構STL的影響

圖6對比了簡支邊界條件和固支邊界條件下，復合板4 種布局AA、BB、BU、UU 在垂直入射下的STL 曲線。AA 結構在第一個板-空氣-板共振頻率以后有很多峰值與谷值，這是由氣腔里面的駐波共振引起的，但在BB、BU、UU 結構里面這種現象就減弱了，這是因為多孔材料展現了強烈的阻尼效應。一直到3000 Hz，AA、BU、UU 結構的STL 在許多頻段都相似。但在3000 Hz 以后，BU 與UU 結構的STL 開始優于AA 結構由于阻尼的影響。在低頻段STL 主要受邊界條件與板的尺寸影響，所以差別不大。縱觀整個頻段，就總體隔聲性能來看，UU 結構隔聲性能最優。

從圖6中還可以看出，簡支邊界條件不僅對AA、BB、BU 和UU 結構在低頻范圍內的STL 有影響，對于中頻和高頻的STL 都有明顯的影響，但是當頻率超過3000 Hz 后，固支和簡支邊界條件下STL基本一致。簡支邊界條件下，4種布局板結構第一個“吻合頻率”都更靠近低頻50 Hz，對比固支邊界條件，第一個吻合頻率更靠近100 Hz。對于AA結構，簡支邊界條件隔聲曲線中“谷值”明顯減少，增加多孔材料后BB、BU、UU 布局復合板結構隔聲曲線中出現的“波谷”都比固支邊界條件下的要少。在小于80 Hz 頻率范圍內，固支邊界條件復合板結構STL 優于簡支邊界條件，但是當頻率超過80 Hz后，在不同的頻率范圍內，簡支復合板結構STL 大于固支邊界復合板STL。

圖6 垂直入射下簡支邊界條件和固支邊界條件4種布局復合板結構STLFig.6 Comparison of STL among various panel configurations with simply supported and clamped boundary conditions under normal incidence

3.4 板尺寸的影響

圖7中分別顯示了在垂直入射下AA、BB、BU、UU四種結構不同尺寸(0.2 m×0.2 m、0.3 m×0.3 m、0.5 m×0.5 m 和無限大)的STL。從圖7中可以看出，由于板尺寸與低頻聲波的波長相比不能被看成無限大，所以除了低頻以外，大尺寸的板的STL 都能很好地近似無限大板的STL。并且，隨著板的尺寸的增加，無限大板與有限大板的傳聲損失差別逐漸變小。

從圖7中還可以看出在第一個隔聲低谷后，由于有限大板的復雜結構模態行為，出現了許多峰值和低谷，并且無限大尺寸還提供了一個STL 漸進極大值。同時在第一個隔聲低谷前，可以看到結構的STL對面板的尺寸和簡支邊界條件很敏感。盡管面板尺寸變化很小，結構的STL 仍變化顯著，并且在板尺寸為0.5 m×0.5 m時，隔聲曲線就已經接近無限大板了。

圖7 AA、BB、BU、UU 結構不同尺寸在垂直入射下傳聲損失的比較Fig.7 Comparison of STL among various panel dimensions under normal incidence for AA, BB,BU and UU configurations

3.5 多孔材料厚度的變化對STL的影響

圖8給出了四邊簡支AA、BB、BU 和UU 結構在垂直入射下不同厚度的多孔材料層的隔聲曲線。計算過程中，板結構參數如表1所示，多孔材料參數如表2所示，3 種布局板結構尺寸都為a=b=0.4 m，BU 結構中空氣層厚度為5 mm，UU結構中空氣層厚度分別為3 mm。從圖8中可以看出，在頻率小于200 Hz 時，改變兩層面板中間空氣層和多孔材料厚度對STL 的影響并不明顯；在低頻段，板的尺寸和邊界條件的影響占主要因素。當頻率超過200 Hz，隨著兩層板中間多孔材料厚度的增加，復合板結構第2 個“吻合頻率”逐漸向低頻移動，3 種結構的STL 在不同的頻率范圍內都有明顯的增加，BB 結構當頻率超過1 kHz 后，STL 明顯增大；BU 結構，在200～1000 Hz 范圍內，STL 隨著多孔材料芯層厚度增加而增加，但是第4 個“吻合頻率”隨著厚度的增加向低頻方向移動，BU 結構高頻段STL 反而會減小。4 種布局中UU 結構，第3 個“吻合頻率”隨著厚度的增加向低頻方向移動，當頻率超過200 Hz，UU 結構隔聲性能在較寬的頻率范圍內都能達到最優。

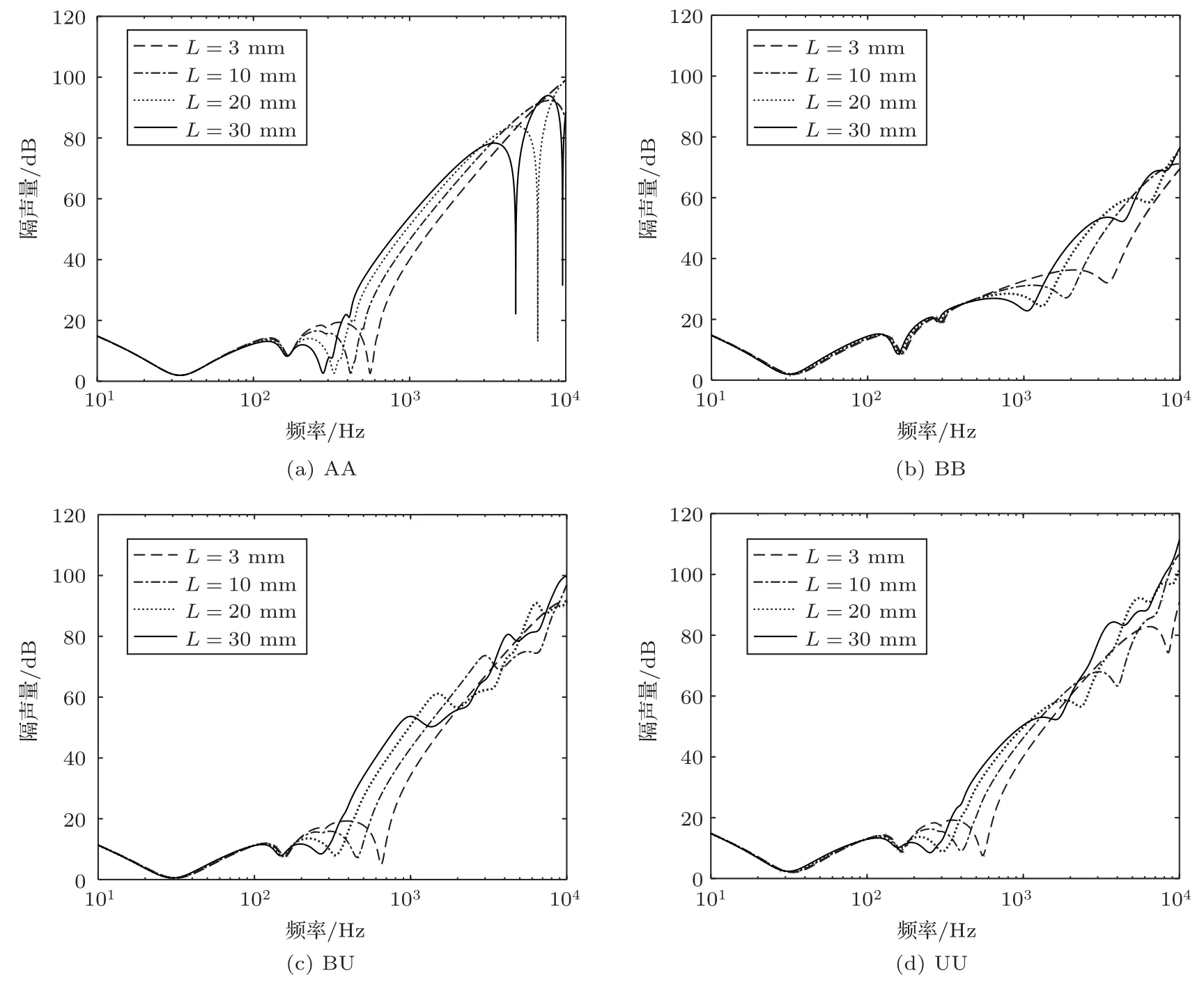
圖8 多孔材料厚度對AA、BB、BU、UU 四種布局復合結構STL 的影響Fig.8 The effect of poroelastic foam thicknesses among AA, BB, BU, UU configuration under normal incidence

4 結論

本文討論了垂直入射下四邊簡支含多孔材料和空氣層分層復合板的隔聲特性，分析了四邊簡支邊界條件、板的有限尺寸、多孔材料芯層厚度對隔聲特性的影響，通過數值結果檢驗了理論模型的收斂性，并與前人的實驗結果對比，理論分析結果與實驗結果具有較好的一致性。

研究結果表明，四邊簡支邊界條件與板的有限尺寸對STL 的影響主要在板-空氣-板共振的低頻段，同時，相比無限大板結構，隨著板的尺寸減小，低頻的STL 顯著提高。在AA、BB、BU、UU 四種結構的隔聲曲線中，UU 結構的隔聲性能是整個頻段上最優的。增加雙層板結構中間多孔材料的厚度，4種布局的復合板結構STL 在較寬的頻率范圍內都有明顯的增加，但是隨著多孔材料的增加，復合板結構在高頻段STL 會降低。因此，對于四邊簡支復合板隔聲性能的聲學設計，需要優化設計多孔材料的厚度，在較寬頻段內獲得更高的STL。

附錄A

矩陣表達式如下：

常量fmn(kx,ky)表達如下：