論以“一題多解”為主題的教研活動對教師成長的促進作用

摘要：一題多解是鞏固所學知識及方法的有效途徑，可以訓練大腦思維的靈活性和發散性，研究一題多解是教師教研的重要課題方向之一，研究一題多解也在促進

教師專業成長中有重要的地位。

關鍵詞：一題多解 教師成長 教研活動

一題多解是從不同角度、不同方位對問題進行思考，尋找不一樣的解決問題的方法及策略。一題多解是實現教師專業化成長的催化劑，久而久之，可以培養教師既全面又深刻、既靈活又善辨的思維能力。協作組內的以“一題多解”為主題的教研活動，可以發揮集體之間的同伴的互助作用，組內成員一起研究某一問題可以更好促進教師個人及教師團隊實現從發展到提升、從創新到超越的目標。

下面舉例來說明以上觀點：

案例：題目：在△中，內角A，B，C的對邊分別是a，b，c，已知.

（1）求角B;

（2）若△為銳角三角形，且，求△面積的取值范圍.

教研活動中，協作組老師先對這道題的常規解法進行了分析，得出一下結論

分析：（1）由題目條件、正弦定理、三角函數恒等變換的應用可知，，可求出，進而可求出的值.

（2）由題目條件和正弦定理，可求出，再結合，可求出，再求出范圍，再根據三角形的面積公式就可求出面積的取值范圍.

解題過程如下：

方法一：（1）由題目條件和正弦定理得，又因為，所以.因為△中，，所以，

所以.又因為，所以，因為.

（2）由題目條件及（1）知△的面積.由正弦定理可得.由于△為銳角三角形，所以，，?由（1）可知，所以，所以，所以，所以.所以，△面積的取值范圍是.

然后協助組教師對本題的考點進行了總結，得出結論：本題考查了正弦定理和三角函數恒等變換的應用，以及三角形的面積公式等知識在解三角形中的綜合應用，同時考查了計算能力和轉化思想，它屬于中檔題.

解題之后，從本問題的結構、問題的條件以及結構之間的內在聯系開始研究，并考慮由問題的條件能否提出不一樣的解法？結論可否做些變化？這些變化又是如何影響問題的？

進一步討論之后，有教師提出，本題第二問的另一種解法M

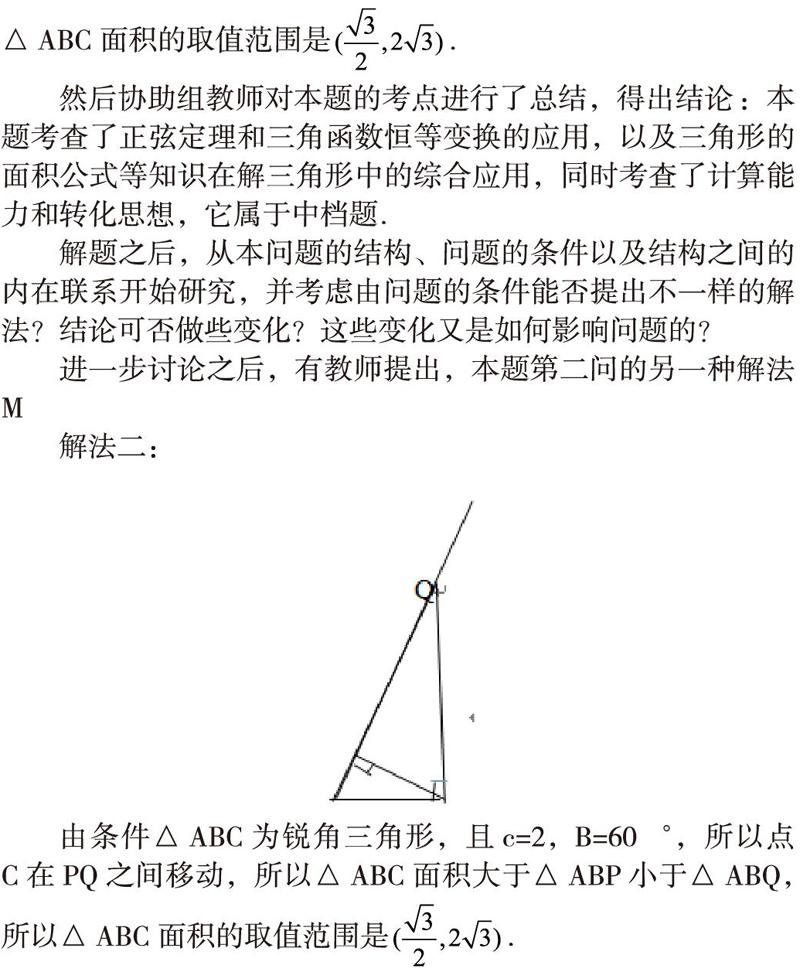
解法二：

由條件△為銳角三角形，且，B=60?，所以點C在PQ之間移動，所以△面積大于△ABP小于△ABQ，所以△面積的取值范圍是.

協作組教師對兩種方法進行了比較，方法一是常規方法，體現計算能力和轉化思想，不能求出△的周長取值范圍，方法二體現數形結合，而且方法二還能輕松求出

△的周長大于△ABP的周長小于△ABQ的周長，也就是說能能求出

△的周長取值范圍。

每當教研活動結束后，都可以給教師們精神愉悅的感受，教研給教師創造了良好的成長環境，是提高教師教學水平的快車道。教研引領教師專業成長，是教師行動研究的最好體現，對提高教師水平十分重要，教研活動中研究“一題多解”是教師專業成長的需要，也是教師主動實踐自我反思的體現。教師要不斷解題，積累經驗，掌握各種解題方法，培養多種解題能力，提升教師專業素質。

“一題多解”為主題的教研活動使教師個人及團隊鉆入教材、跳出教材、超越教材，多角度，多渠道多全方位認識知識。以“一題多解”為主題的教研活動又能集中智慧與力量，活躍思維，啟發思考，在思維培養方面的能力功能十分顯著。教研令從事教師職業成為一種享受，一種快樂，一種力量，也讓教師的成長永不止步。

【參考文獻】

[1]《高考總復習優化設計》2020.01

[2]《新課程標準》?2018.0

河南省安陽市殷都區正一中學分校 鄭敬敏