數形結合思想在小學數學教學中的運用探究
楊小文
(寧夏回族自治區中衛市沙坡頭區鎮羅鎮凱歌學校 寧夏中衛 755000)
小學生生活經驗少、認知能力不足,抽象思維和邏輯思維都不強[1]。而數學作為一門抽象學科,在學習的時候要想讓學生充分理解數量之間的關系,能夠對問題進行證明推導,有效解決,就要重視學生的思維能力的培養。數形結合思想在數學中的應用,為學生思維能力的發展提供了平臺,既可以培養數學建模素養,又可以促使知識點化繁為簡,化抽象為形象,提高解決問題的能力。本文就數形結合思想在小學“數與代數、圖形與幾何、相遇應用問題”等四個知識領域中的應用進行了探究分析。
一、在數與代數中滲透數形思想,培養數學抽象素養
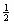
二、在圖形與幾何中滲透數形思想,培養直觀想象素養
圖形與幾何的學習可有效培養的學生的直觀想象素養,促進學生空間思維的發展[2]。但小學生理解能力、思維能力的發展都比較薄弱,要想讓學生在學習圖形與幾何的時候有一個清楚的理解,首先要幫助學生形成空間思維,在提高學生空間感知能力的同時,通過數形結合思想的滲透,幫助學生學習圖形與幾何知識內容。例如,教學“長方形和正方形”,旨在讓學生了解長方形和正方形的特點,能正確運用周長公式進行計算,使其形成初步的空間觀念。對此,在教學時,教師可以引導學生觀察數學課本,以數學課本為載體,為其準備尺子、剪刀、三角板等,讓學生動手量一量、剪一剪,裁剪長方形和正方形圖形,在制作圖形的過程中,讓學生根據所量得的數據及觀看情況分析一下長方形的角、各邊有什么特點,在動手操作實踐、直觀觀看的過程中,滲透數形結合思想,培養學生的直觀想象和數學建模素養,然后以對長方形和正方形特點的了解為基礎,就其圖形的周長公式展開探索,促進學生對數學公式的理解,這樣既可以達到靈活記憶的目的,又可以培養學生的數學學習技巧。
三、在應用題解析中滲透數形思想,培養數學建模素養
應用問題解析是數學教學重點,也是學生考試的重點。但受傳統講授教學法的影響,應用問題的解析教學效果并不理想,而數形結合思想的應用,不僅可以促使這一抽象問題得到形象解決,還可以優化解題思路,提高學生對應用問題的解題自信心。例如,在解決相遇形成問題的時候:
余剛和苗苗約定9:00同時從自己家去少年宮,9:16兩人正好在少年宮相遇,已知余剛每分鐘走75米,苗苗分鐘走70米,思考:他們兩家相距多少米?
解決這一問題的時候,教師要讓學生先分析題干信息,根據所學知識點,思考相遇問題其考點的核心公式有哪些,如:路程=速度×時間;相遇的路程=速度和×相遇時間;相遇路程÷相遇時間=速度和;相遇路程÷速度和=相遇時間。在認識所考知識點內容的基礎上,讓學生分析一下相遇的時間是什么時候,然后根據題干信息轉化為直觀圖形:
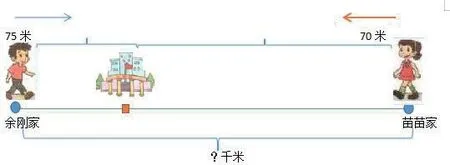
根據圖形引導其思考兩人行走的方向是怎樣的,當兩人相遇時,他們所走的路程與兩人家相距多少米有什么聯系。在問題思考的過程中,讓學生知道:兩家相距的路程正好是他們16分鐘所走的路程之和,從而列出(75+70)×16解決公式,使問題迎刃而解,數形結合思想在應用問題中的應用,可培養學生的數學建模素養,提高問題解決質量。
四、結束語
數形結合思想在小學數學教學中的運用,不僅可以化解抽象的知識點,培養學生的數學抽象素養,還可以提高學生的問題解決能力,促進學生的思維發展,使其掌握數學學習技巧。因此,教師要重視數形思想在數與代數、圖形與結合、應用題解題中的利用,通過數形結合,幫助學生理解抽象概念,培養學生空間思維,優化解題路徑。

