循環球電動助力轉向系統控制及補償策略*

魏 娟，李子卓，田海波

(西安科技大學機械工程學院,陜西 西安 710054)

1 引言

循環球式電動助力轉向系統EPS(Electric Power Steering)是基于循環球式機械轉向器結構，將電機作為轉向助力能量來源的助力轉向系統。相較于循環球結構液壓助力轉向系統，采用電機助力更便于對轉向輕便性與路感進行調整控制[1]，還使得車輛的操縱穩定性獲得了更有力的保證[2,3]。

隨著技術發展進步，圍繞汽車電子控制系統所進行的研究工作愈發深入，其中，對電動助力轉向系統的研究，便是一個重要方向。在現有EPS改進的方法上，很多研究人員從建立模型入手，如Ciarla等[4]通過建立摩擦接觸模型的方法，分析驗證了轉向助力曲線設計中助力力矩與轉向盤轉角的關系；Zhu等[5]通過研究駕駛員行為，做出了電動助力轉向系統個性設計，取得了理想效果。

電機助力的方式更易于通過設計控制算法和補償策略，來達到更好的轉向輕便性及路感，如Sugita等[6]為了提高EPS動態特性，設計了包括阻尼補償、慣性補償及振動抑制的補償控制器；Morita等[7]提出了基于解耦控制的變速齒輪傳動系統電動助力轉向系統控制器設計方法；Lee等[8]采用自適應滑膜控制，開發了轉向助力力矩控制算法，用以改善傳統控制方法，提高了電動助力轉向系統的魯棒性。

上述針對提高EPS的動態特性的研究，都實現了相應目的，但目前EPS的多數研究都是針對齒輪齒條結構的轉向器，其結構相對循環球式轉向器更簡單，控制算法和補償策略都不能直接套用。具體到國內的循環球式電動助力轉向系統控制，目前趙萬忠等[9,10]開發了純電動客車的2層助力特性控制策略，而后又通過設計混合H2/H∞控制器，得到了更好的動態特性；申榮衛等[11]也在純電動客車的循環球式電動助力轉向系統開發過程中設計了控制策略，并基于經典控制理論，對控制結果可能存在的多因素影響設計了相應補償策略。上述針對循環球式電動助力轉向系統的研究未涉及相應補償策略的算法及建模方法，補償結果尚存在改進空間。

由此，本文通過建立循環球式電動助力轉向系統模型及其控制策略，實現有針對性的控制方案；并基于LuGre摩擦模型，設計摩擦狀態觀測器，通過自適應算法控制，實現摩擦補償控制。

2 系統建模

循環球式電動助力轉向系統是由機械轉向器、轉矩轉角傳感器、車速傳感器、電動機及其減速機構和電子控制單元ECU(Electronic Control Unit)等構成。車輛駕駛員意圖轉向時，轉矩傳感器檢測到轉向盤轉矩，信號被輸送到ECU，ECU根據轉矩信號、車速信號等，控制電機輸出轉向助力力矩。

2.1 循環球式轉向器模型

循環球式電動助力轉向系統的結構，在進行適當簡化后，得到包含駕駛員模型的動力學方程為：

(1)

其中,G(s)為駕駛員模型輸出轉矩；Kp為比例系數；s為目標轉角與實際轉角之差；Kd為微分系數；Ki為積分系數；τ為延遲時間；Tsw為轉向盤輸入轉矩，Jsw為轉向盤等效轉動慣量；θsw為轉向盤轉角；Bsw為轉向盤等效阻尼系數；Tsc為轉向軸傳遞力矩；θsc為轉向柱轉角;θm為電機轉角；Ksc為轉向軸轉動慣量，x為螺母位移;m為轉向螺母質量；B為阻尼系數；Rse為齒扇半徑；θp為搖臂轉角；Tassist是電機助力力矩；t表示螺母桿轉動1圈時螺母位移量；Tse為齒扇轉矩；Jp為搖臂轉動慣量；Bp為搖臂阻尼系數；Trm為繞主銷轉向阻力矩。

助力電機采用直流電機，通過蝸輪蝸桿減速機構與轉向器機械結構連接，其簡化模型為：

(2)

其中,Ta為電機電磁轉矩；Ja為電機轉動慣量；Ba為電機阻尼系數；U為電樞電壓；R為電樞電阻；I為電樞電流；L為電樞電感；Ke為反電動勢常數；Tm為電機輸出力矩，Tassist是電機助力力矩；Kt為電機轉矩系數；Gm為減速器傳動比；Ja為電機軸轉動慣量；Ba為電機軸等效阻尼系數；θa為電機轉角；θm為電機輸出轉角；Gm為減速機構減速比；Km為減速機構扭轉剛度。

2.2 整車建模

汽車是一個極為復雜且耦合度高的系統，簡化的二自由度模型無法對整車性能進行全面的描述。且在進行補償控制策略的研究中，補償電流本身就非常小，更需要精確的整車模型。因此，本文采用CarSim軟件中的整車模型，并搭建了CarSim與Matlab/Simulink聯合仿真平臺。

2.2.1 參數設置

根據現有布置循環球式轉向器車輛的實際需要，選擇前驅形式越野車車型，在CarSim中修改系統提供車型參數，以符合所研究某車型的具體條件。

2.2.2 外部環境及工況設置

聯合仿真中轉向系通過Matlab/Simulink設計控制，在CarSim中關閉助力的轉向系統。外部環境及工況選擇默認參數設置，運行工況通過Matlab/Simulink中模型調節，關閉軟件中轉向調節。在系統內將前輪轉矩設置為CarSim整車模型輸入，整車模型輸入繞主銷的前輪回正力矩。

2.3 阻力矩模型

根據車輛轉向阻力矩構成特點，將轉向阻力矩動力學模型按車速分別建模。

2.3.1 原地、低速行駛時模型

(3)

(4)

Tzmax=Tr/Gr

(5)

其中,Tz為轉向阻力矩，Kz為等效扭簧剛度系數，θp為齒扇轉角;Tr為原地轉向時阻力矩；μz為滑動摩擦系數；Gf為轉向軸載荷；Pt為輪胎氣壓；Gr為齒扇至轉向輪間傳動比。

2.3.2 中高車速行駛時模型

汽車在高速行駛時，輪胎與路面間的摩擦阻力矩和轉向系統內部摩擦力矩可忽略不計，此時，將CarSim整車模型中輸出的主銷回正力矩視為轉向阻力矩。

3 控制過程

3.1 電流助力曲線

設計電流助力曲線時，一般僅考慮車速v和轉向盤轉矩Tsw2個參數的影響，經計算，可得：

(6)

(7)

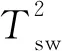
(8)

其中,Ia為電機目標電流；Tsw0為助力轉矩死區值；Tswmax為目標電流最大時的轉向盤轉矩值；K(v)為與車速有關的助力增益函數；f(Tsw)為目標電流與轉向盤轉矩的函數。

3.2 電流模糊PID控制

助力過程中需要采用跟蹤算法實現對目標電流實時準確的跟蹤，跟蹤精度直接決定系統的性能。又由于EPS實際上是一個復雜的受多因素影響的隨機系統，所以需要設計一種可以對目標電流實現準確、實時跟蹤，且有較強魯棒性的控制策略。

模糊PID控制將模糊控制的強適應性與PID控制的高精度性相結合，通過模糊控制規則對PID參數進行在線調整，提高系統的動態性能，其控制方法如圖1所示。

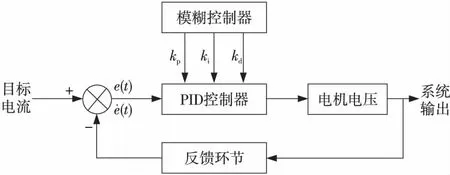
Figure 1 Fuzzy PID control method圖1 模糊PID控制方法

模糊控制器的輸入量為目標電流與實際電流的偏差和該偏差的變化率，將其論域及所需要控制的PID參數kp,ki,kd的論域均采用{NB，NM,NS,O,PS,PM,PB}7種模糊語言變量進行描述。根據不同參數所需的不同論域，分別設置kp,ki,kd3個參數的隸屬度分布情況,如圖2～圖4所示。

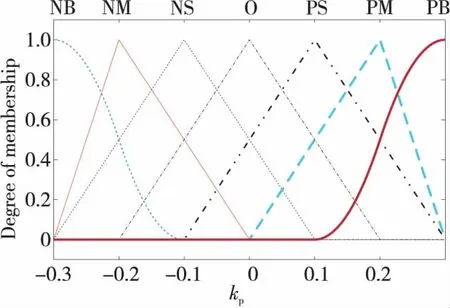
Figure 2 Distribution of membership function of kp圖2 kp的隸屬度函數分布圖

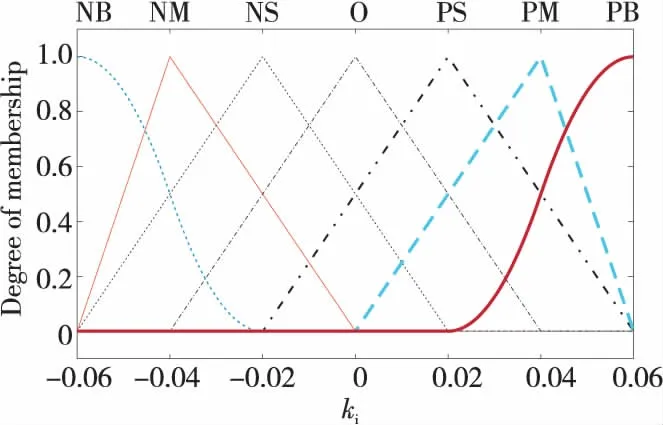
Figure 3 Distribution of membership function of ki圖3 ki的隸屬度函數分布圖

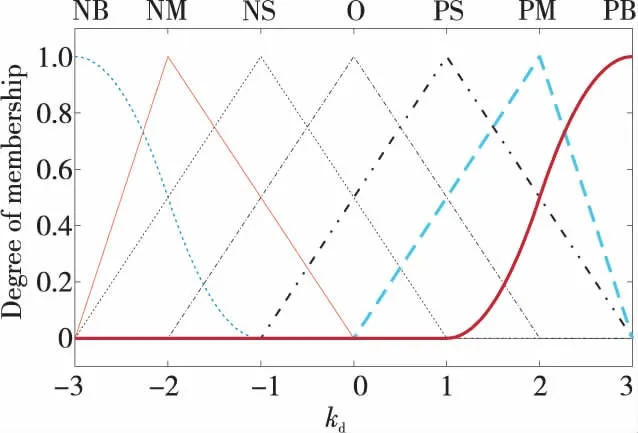
Figure 4 Distribution of membership function of kd圖4 kd的隸屬度函數分布圖

電機電壓的控制規則選取原則為：

當|e(t)|較大時，可選取較大的kp與較小的ki，使系統快速響應，同時為了避免出現較大的超調，應對積分作用加以限制，常取ki=0。

當|e(t)|較小時，為了使系統應具有較小的超調，kp應取較小，ki應取適當值，kd取值對系統的影響較大。

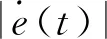
3.3 摩擦補償控制策略

對于汽車轉向系而言，摩擦力矩的存在影響了駕駛員對路感的判斷，減緩了機械系統中的響應速度，削弱了助力補償力矩。為明確實際回正力矩大小，更準確地獲得路感信息，對轉向系產生的摩擦力矩設計一種LuGre摩擦模型的自適應摩擦補償控制策略。

LuGre摩擦模型采用鬃毛思想，如圖5所示，將系統的接觸面等效視為大量具有隨機行為的彈性鬃毛，由于鬃毛的形變，產生摩擦力[12]。

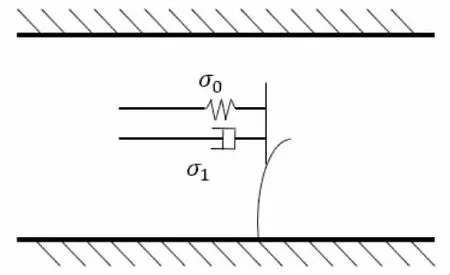
Figure 5 Schematic diagram of LuGre friction model圖5 LuGre摩擦模型示意圖

為便于建模及設計控制程序，對普通LuGre摩擦模型進行離散化處理，設離散采樣時間間隔為ΔT,離散時間用k表示，得到的模型如式(9)所示。

(9)

其中,σ0為鬃毛平均剛度；σ1為鬃毛阻尼系數；σ2為粘性摩擦因數(該部分在轉向系統內不考慮)；Mfc為庫侖摩擦力矩；Mfs為最大靜摩擦力矩；z(k)為模型位移；g(k)為用以描述Stribeck現象的函數；y(k)為描述Stribeck現象的函數；v(k)為k時刻的速度；Mf即為所求的摩擦力矩。

使用文獻[13]中的摩擦參數辨識方法，經由LuGre模型計算得到摩擦消耗力矩，將其全部等效至轉向齒扇處，與輸入力矩疊加，可獲得經補償控制后的目標電流。

4 仿真驗證

在CarSim和Matlab/Simulink軟件中分別建立整車模型及轉向助力模型，運用本文設計的循環球式電動助力轉向控制策略進行仿真分析，仿真關鍵參數如表1所示。

Table 1 Vehicle parameters表1 整車參數

4.1 轉向系統控制效果驗證

為驗證循環球式電動助力轉向系統控制效果，設計了仿真分析驗證工況，在行駛車速為20 km/h時，駕駛員模型設定目標轉角16°，維持2 s，驗證整車的轉向及回正情況。結果如圖6所示。

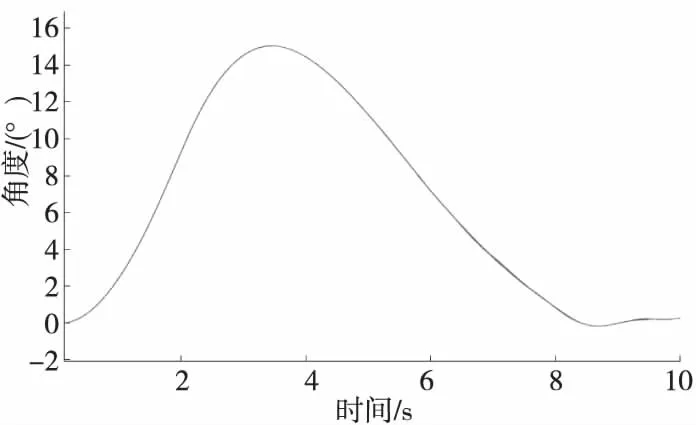
Figure 6 Wheel angle change diagram圖6 車輪轉角變化圖

通過觀測車輪轉角變化圖可知，在該行駛工況下，加載并維持階躍輸入轉向盤轉角，聯合仿真系統可在短時間內完成車輪轉角的輸出，并在取消階躍輸入后，車輛可在短時間內自動回正，仿真結果驗證了聯合仿真系統的有效性。

圖7為在CarSim軟件中監測得到的車輛側向加速度變化趨勢圖，在第2 s時，系統加載輸入取消，可觀測到側向加速度呈現下降趨勢，在6 s末，曲線震蕩維持在0附近。鑒于CarSim中，車輛工況復雜，曲線應存在一定震蕩幅度，且該條曲線震蕩趨勢符合轉向系統轉向后自動回正的特性。

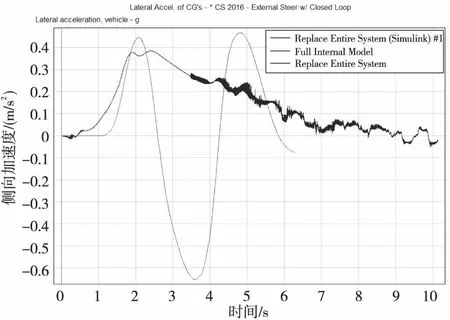
Figure 7 Lateral acceleration change diagram in CarSim圖7 CarSim中側向加速度變化圖

4.2 LuGre模型自適應補償效果驗證

為了驗證LuGre摩擦模型的自適應補償控制效果，保持其他仿真驗證工況不變，既在行駛車速為20 km/h時，駕駛員模型設定目標轉角16°，維持2 s，觀察采用摩擦補償后，補償能否產生作用，并觀察車輛回正情況。

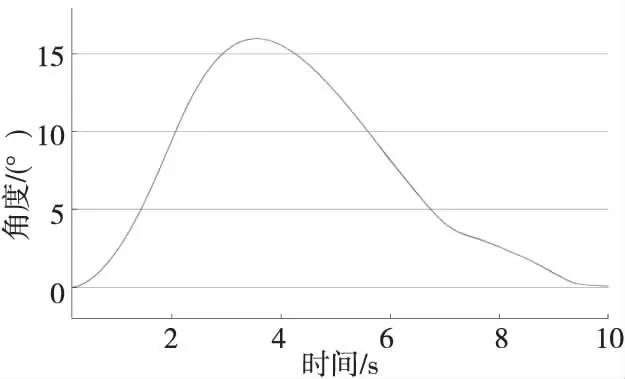
Figure 8 Wheel rotation angle change after friction compensation圖8 LuGre摩擦模型的自適應補償后車輪轉角變化圖

仿真結果(如圖8所示)與補償前結果對比，可明顯觀察到，通過LuGre摩擦模型的自適應補償，車輪轉角峰值提高1°，更加接近目標轉角，且車輪回正時間相近，回正速率更加平穩。因此，在系統內加入摩擦補償設計，相較于補償前，提高了轉向角度輸出，更準確地體現了轉向意圖。

5 結束語

(1)分析了循環球式電動助力轉向系統各組成模塊的數學模型，分別搭建了基于Matlab/Simulink的轉向系統模型和基于車輛仿真軟件CarSim的整車模型。

(2)設計了基本助力控制，在此基礎上通過搭建模糊PID控制的電機控制策略，實現了對電機電流的實時跟蹤控制。

(3)采用了搭建摩擦狀態觀測器的方法，獲取系統產生的摩擦力矩，實現對轉向過程中系統內摩擦造成的力矩損失的補償，使汽車轉向更加準確和穩定。

(4)通過仿真分析，首先驗證了聯合仿真模型的有效性；通過LuGre摩擦模型并采用狀態觀測的方法，能更準確地實現駕駛員駕駛意圖，使得回正過程更加平穩。