汽輪機低壓扭葉片強度和振動的可靠性分析*
田澤瑜,魏佳明,李祎曼,盧紅遠,米海波
(1.杭州汽輪機股份有限公司,浙江 杭州 310006;2.杭州汽輪動力集團有限公司,浙江 杭州 310006)
0 引 言
汽輪機葉片是汽輪機的關鍵部件,其安全可靠性直接關系到汽輪機和整個電站的安全。汽輪機低壓級扭葉片在運行時承受巨大的離心力、蒸汽力、蒸汽激振力等的共同作用。目前,廣泛采用確定性強度振動設計準則對汽輪機葉片進行校核。但是實踐證明,由于汽輪機葉片在實際加工和使用過程中,其材料屬性、幾何尺寸、工作條件等都存在隨機性,受此影響,汽輪機葉片強度和振動特性也存在一定的分散性。傳統(tǒng)強度振動設計準則是把所有設計變量看成是定值,并保證一定的安全裕度,沒有充分考慮參數(shù)的隨機性,不能預估設計風險。
鑒于確定性強度振動分析方法存在弊端,需要對汽輪機葉片進行強度振動可靠性研究。近年來很多學者從多方面對結(jié)構(gòu)可靠性進行了研究與分析。基于概率的可靠性分析方法在目前結(jié)構(gòu)可靠性分析方法中應用最為廣泛。艾書民等[1]采用Monte-Carlo法對某型發(fā)動機第一級渦輪轉(zhuǎn)子葉片進行了可靠性分析;劉占生等[2]基于Monte-Carlo法,研究了重型燃氣輪機壓氣機葉片的材料屬性、葉高和葉片安裝值對壓氣機葉片強度影響;段巍等[3]基于響應面方法,考慮隨機因素的影響,對汽輪機直葉片進行了靜動頻概率設計及敏感性分析。
針對上述分析,本文采用基于概率分析的可靠性分析方法,并將有限元-二階多項式響應面-Monte-Carlo法相結(jié)合,對某汽輪機低壓扭葉片開展可靠性分析,得到可靠度。最后對葉片強度振動進行概率敏感性分析,得到隨機參數(shù)對其影響程度[4-6]。
1 強度振動可靠性分析方法
1.1 可靠度計算
葉片可靠度是指葉片在規(guī)定條件下和規(guī)定時間區(qū)間內(nèi)完成規(guī)定功能的概率。可靠度數(shù)值范圍在0~1之間,可靠度數(shù)值越大,結(jié)構(gòu)失效概率越低。同時,可認為當樣本數(shù)足夠多的時候,可靠度的置信度趨近于100%。
葉片靜強度可靠度[7]的求解如下:
(1)
式中:fl(xl)—應力概率密度;fs(xs)—強度概率密度。
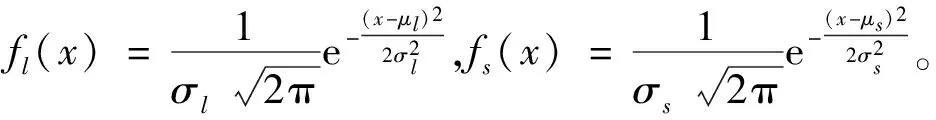
計算葉片動應力時,由于激振因子的取值有待深入研究,工程上采用安全倍率法。
當影響安全倍率Ab的各參數(shù)都服從正態(tài)分布,且相互獨立時,葉片動強度的可靠度[8]可求解如下:
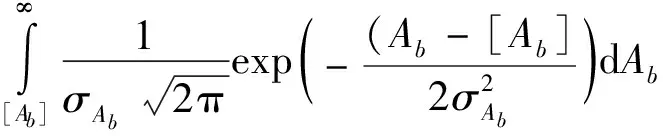
(2)
葉片振動的可靠度計算需考慮葉片振動頻率和激振頻率的分布特性。對于整圈成組葉片,其振動設計需避開三重點共振。當葉輪上的葉片整圈成組連接時,對于節(jié)徑數(shù)m≠0的振型,必須同時滿足3個條件才能避免共振,即:
(1)節(jié)徑數(shù)為m的葉片固有頻率與激振力第k階諧波的頻率kns不重合,即fm≠kns;
(2)節(jié)徑數(shù)m與諧波階數(shù)k不重合,即m≠k;
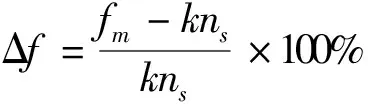
因此,對于任何整圈成組葉片,其振動可靠度[9]可求解如下:
R=Rk*Rm*RΔf
(3)
式中:Rk—節(jié)徑數(shù)為m的振型時整圈葉片組動頻fd避開kns的概率;Rm—fd避開mns的概率;RΔf—fd與kns的避開率滿足共振安全率要求的概率。
1.2 有限元-響應面-Monte-Carlo方法
有限元-響應面-Monte-Carlo方法[10]的基本思路是:在結(jié)構(gòu)的真實響應Y未知的情況下,假設Y與影響結(jié)構(gòu)的隨機參數(shù)矢量X=[X1,X2,…XNR]的關系可用某種函數(shù)描述。用某種取樣方法得到隨機參數(shù)矢量的NS個樣本,對這NS個樣本點進行數(shù)值分析,得到結(jié)構(gòu)響應的一組樣本點,通過回歸分析得到響應面函數(shù),在以后的分析中用響應面函數(shù)代替結(jié)構(gòu)的真實響應。
本文以某汽輪機組低壓扭葉片為研究對象,其方法流程圖如圖1所示。
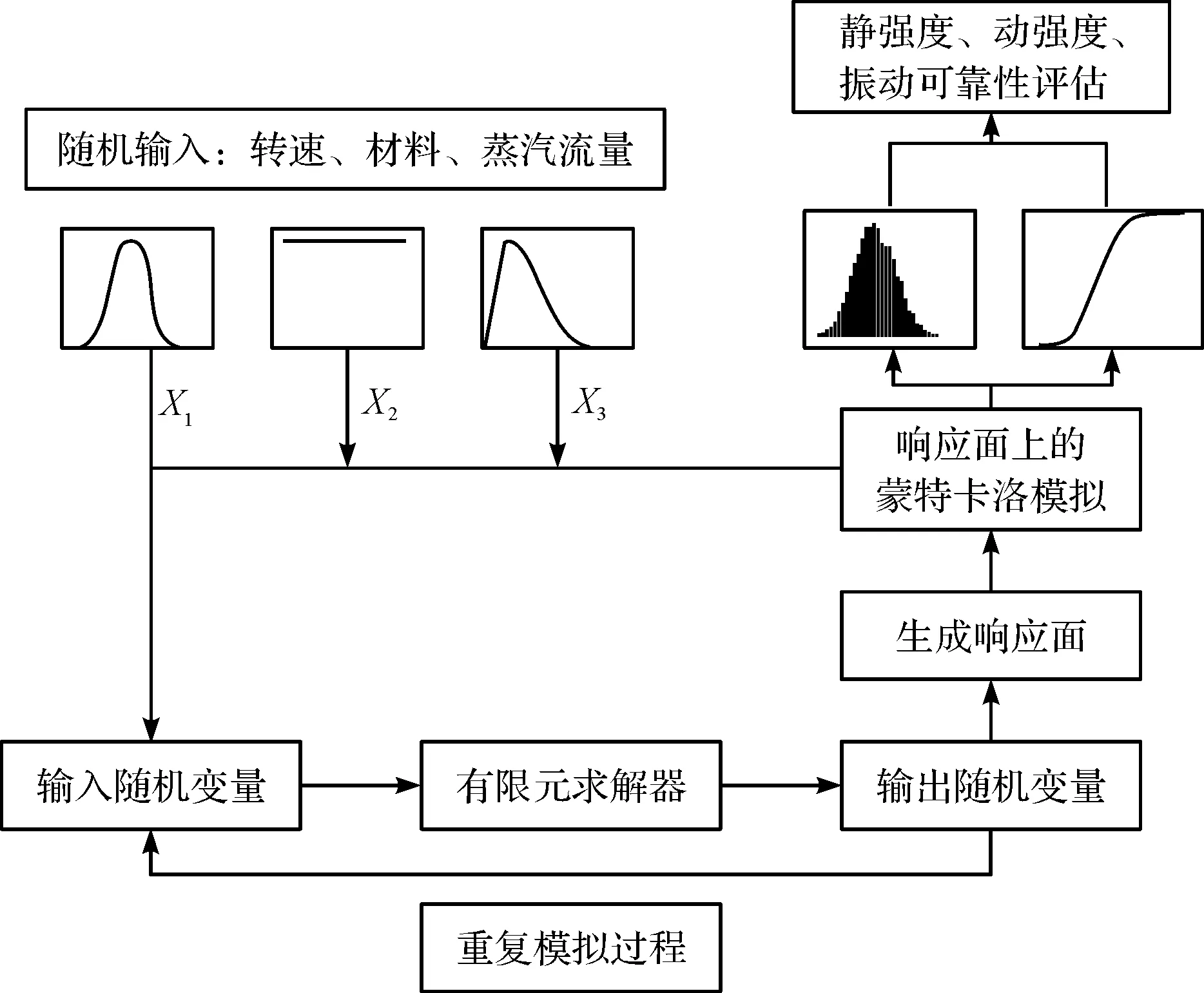
圖1 方法流程圖
圖1中,首先輸入各隨機變量的分布類型,然后采用有限元-二階多項式響應面-Monte-Carlo法,分別計算葉片的靜強度、動強度以及振動的可靠度。
同時,本文研究了隨機因素對強度和振動的概率敏感性,得到了主要因素。
2 實例及結(jié)果分析
本文研究對象為某汽輪機低壓級組葉片,該葉片為整圈成組的扭葉片,材料為2Cr13,葉高為329 mm。
2.1 靜強度可靠性分析
汽輪機葉片葉身的靜應力由3部分組成,即σst=σct+σcb+σsb(其中:σct—離心拉應力;σcb—離心彎應力;σsb—汽流彎應力)。
首先通過流場分析,獲得葉身的壓力場分布,并將壓力場結(jié)果賦到葉身表面;同時對葉片施加轉(zhuǎn)速,獲得葉身應力場分布。
本研究在CFX19.0中,對低壓葉片級進行氣動分析,設置入口和出口邊界條件。
低壓級葉片氣動場分布如圖2所示。

圖2 低壓級葉片氣動場分布
圖2中,透平進口蒸汽總壓2 bar,進口總溫130 ℃,水蒸氣干度0.99;出口平均靜壓0.09 bar;葉片表面采用無滑移邊界條件,CFD計算使用k-ε湍流模型。
在ANSYS19.0中,本文對葉/盤模型進行靜強度分析。
葉/盤三維模型如圖3所示。

圖3 葉/盤三維模型
圖3中,為減少計算量,本研究截取1/87扇區(qū),對葉/盤進行網(wǎng)格劃分。其中,對葉根、葉槽以及圍帶進行網(wǎng)格細化,并設置接觸對;對葉/盤設置循環(huán)對稱邊界條件,并施加轉(zhuǎn)速,同時將CFD計算得到的氣動場數(shù)據(jù)賦到葉身表面。通過有限元分析獲得葉身等效應力分布。
影響靜強度的隨機參數(shù)及統(tǒng)計特性如表1所示。
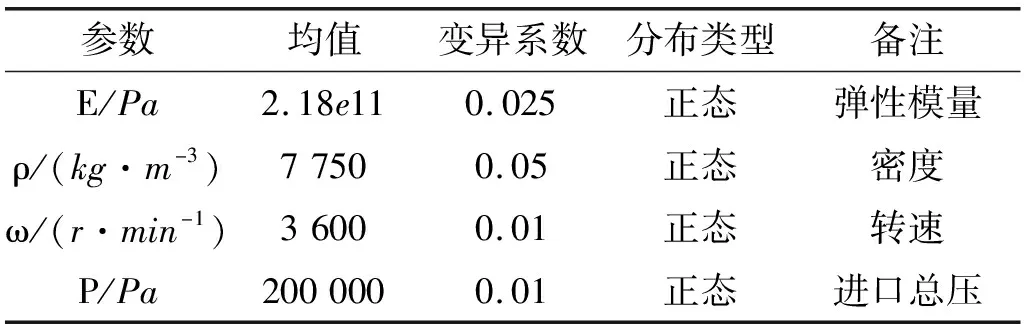
表1 隨機參數(shù)及統(tǒng)計特性
注:當出口壓力變化不大時,進口流量與進口總壓成正比,方便敘述,將進口壓力的變化等同于流量的變化
其中,隨機輸入變量為4個,根據(jù)隨機輸入變量的個數(shù),采用中心合成抽樣法[11],并確定所需樣本數(shù)量為25個。調(diào)用確定性有限元分析25次,得到用以擬合響應面的樣本點。
本研究采用標準二次多項式進行響應面擬合,并用響應面代替有限元計算結(jié)果。
同時,采用Latin Hyercube樣本法生成模擬樣本,并用Monte-Carlo法對樣本抽樣105次,經(jīng)過統(tǒng)計分析,得到葉身等效應力概率分布函數(shù),如圖4所示。
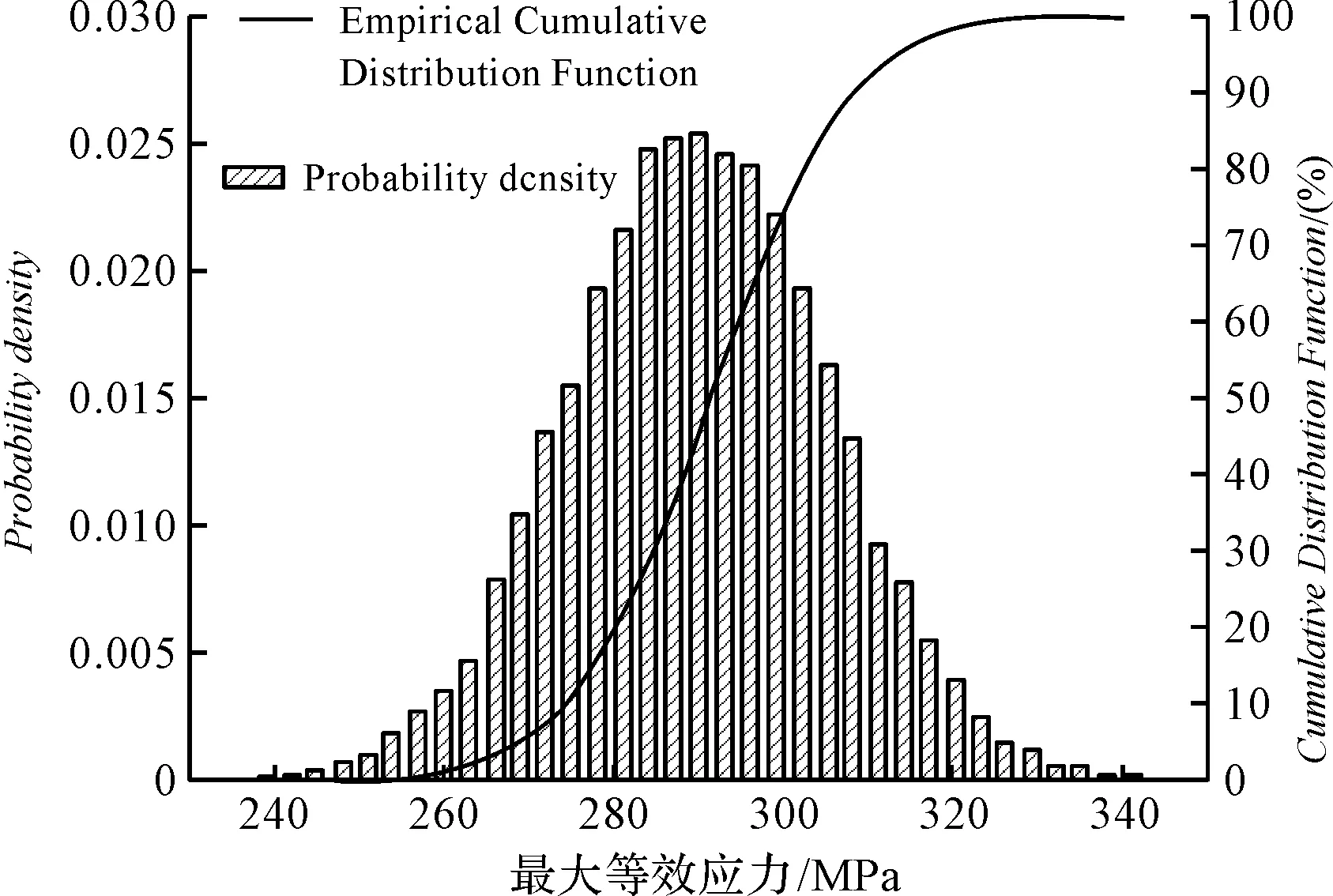
圖4 葉身等效應力概率分布函數(shù)
圖4中,葉身最大等效應力均值為291.71 MPa,標準方差為15.35 MPa。
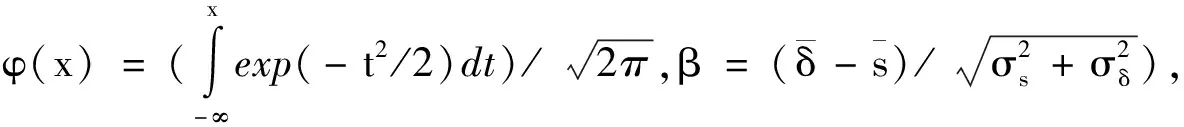
可以看出,只考慮葉片靜強度失效時,在該工況下葉片能夠安全可靠地工作。
同時,本文研究了各隨機參數(shù)對葉身最大等效應力的概率敏感性。
葉片靜強度概率敏感性分析結(jié)果如圖5所示。
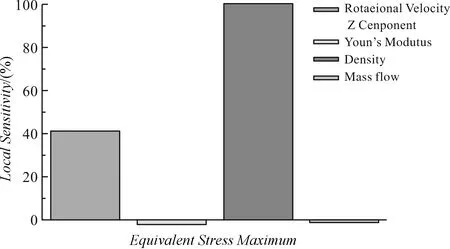
圖5 葉片靜強度概率敏感性分析結(jié)果
圖5中的分析結(jié)果表明:材料密度對葉身等效應力的影響最大,轉(zhuǎn)速次之,彈性模量及蒸汽流量對葉身等效應力影響較小;其中,轉(zhuǎn)速、密度、蒸汽流量與葉身等效應力成正相關,彈性模量與葉身等效應力成負相關。
2.2 動強度可靠性分析
葉身安全倍率如下式所示:
(4)
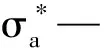
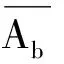
(5)
(6)
因Ab服從正態(tài)分布,有:
(7)
根據(jù)葉片尺寸及工作環(huán)境,本文獲得隨機參數(shù)均值,并根據(jù)文獻[12]得到截面變異系數(shù)及分布類型。
0%葉高截面的隨機參數(shù)及統(tǒng)計特性如表2所示。
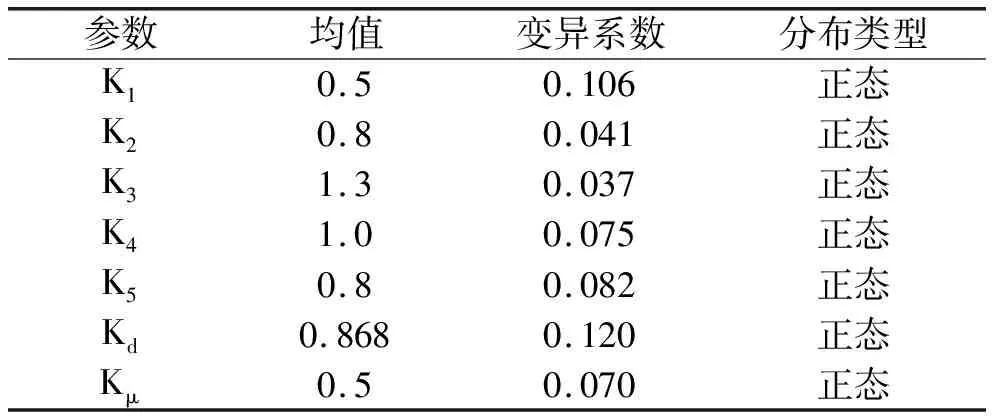
表2 隨機參數(shù)及統(tǒng)計特性
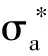
由此可以看出,只考慮動強度失效時,葉片在該工況下未能達到99.73%的要求(±3σ準則)。
2.3 振動可靠性分析
在ANSYS19.0中,本研究對葉/盤模型進行頻率分析。首先開展葉/盤的靜力分析,并進行基于預應力的頻率分析[13],得到葉片組的頻率及振型圖。
本文統(tǒng)計了影響葉片組頻率的隨機參數(shù)及統(tǒng)計特性,如表3所示。
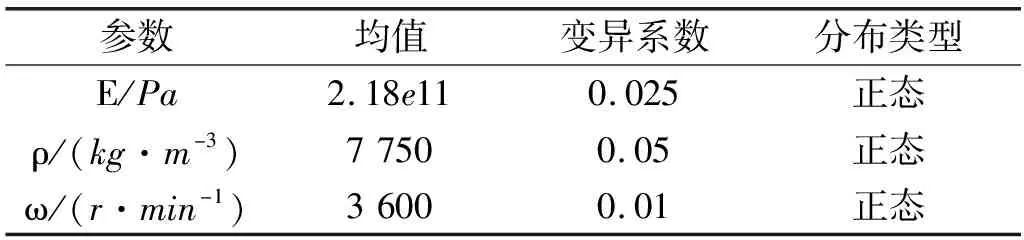
表3 隨機參數(shù)及統(tǒng)計特性
其中,隨機輸入變量為3個,根據(jù)隨機輸入變量的個數(shù),采用中心合成抽樣法,并確定所需樣本數(shù)量為15個。調(diào)用確定性有限元分析15次,得到用以擬合響應面的樣本點。
本文采用標準二次多項式進行響應面擬合,并用響應面代替有限元計算結(jié)果。
同時,筆者采用Latin Hyercube樣本法生成模擬樣本,并用Monte-Carlo法對樣本進行抽樣105次,得到前6節(jié)徑頻率均值和方差,如表4所示。
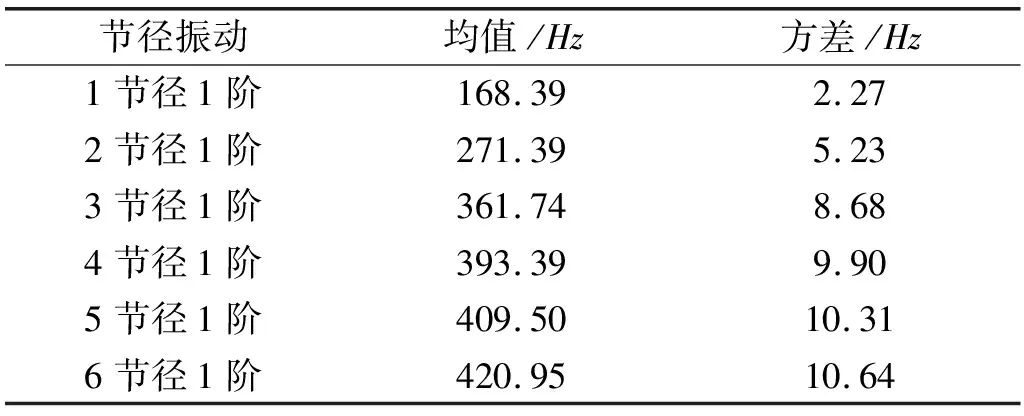
表4 前6階頻率均值和方差

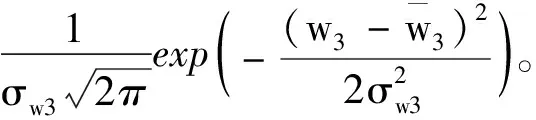
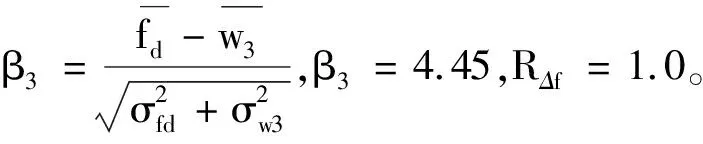
由此可以看出,只考慮振動失效時,葉片在該工況下能夠安全可靠的工作,避開率滿足3%。對于其余節(jié)徑振動,同樣可得可靠度R=1.0。
本文研究了隨機參數(shù)對葉片組頻率的概率敏感性。頻率概率敏感性分析結(jié)果如圖6所示。
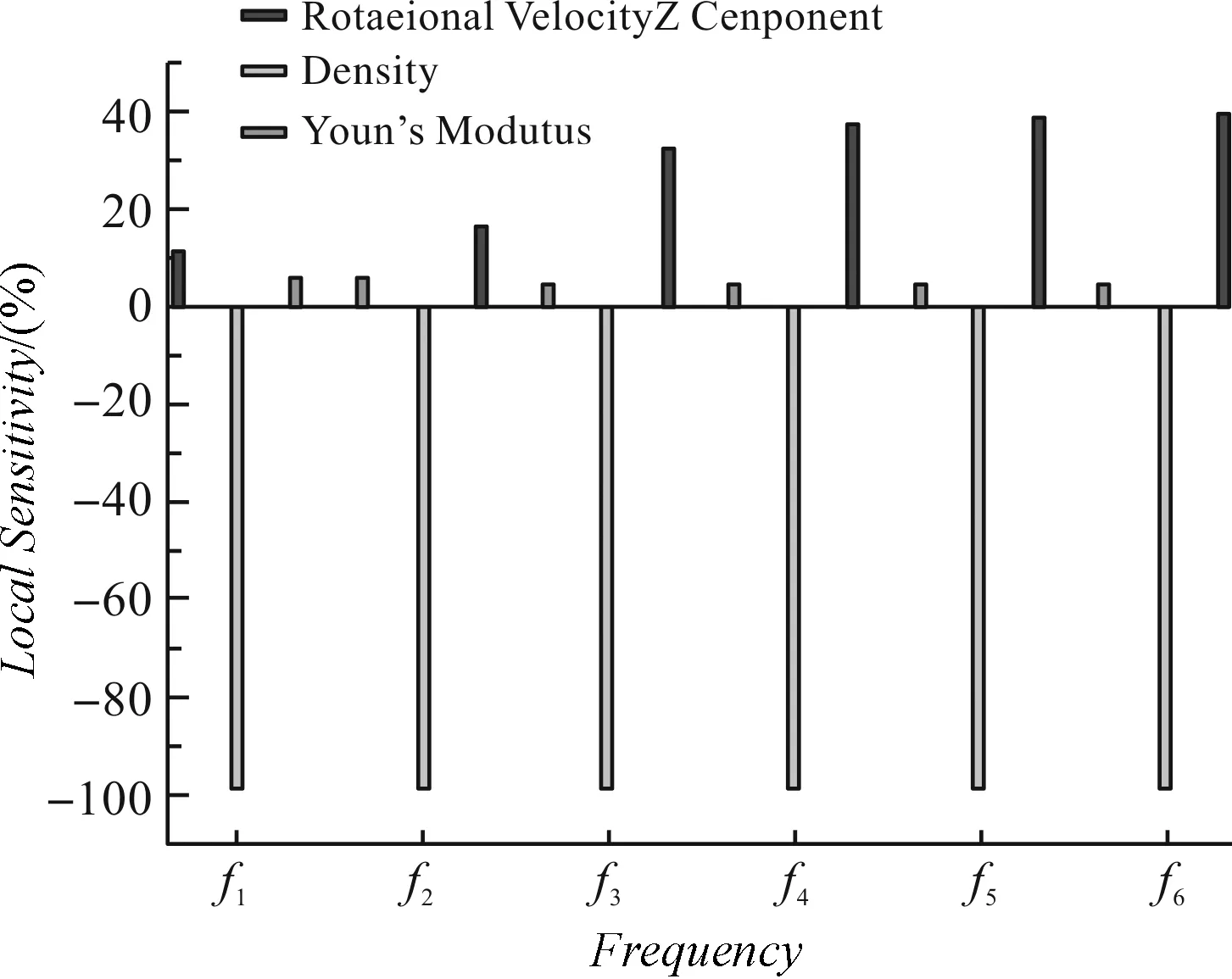
圖6 頻率概率敏感性分析結(jié)果
圖6中的分析結(jié)果表明:對于不同節(jié)徑的頻率,材料密度對葉片組頻率影響最大,且成負相關;隨著節(jié)徑數(shù)增大,彈性模量對頻率的影響增大,轉(zhuǎn)速對頻率的影響減小,但都是成正相關。
3 結(jié)束語
在考慮了汽輪機低壓扭葉片材料、轉(zhuǎn)速、蒸汽流量分散性的基礎上,本文采用有限元分析法、響應面法和Monte-Carlo隨機模擬法相結(jié)合的方法,獲得了汽輪機低壓扭葉片強度振動可靠度,同時,對強度振動進行了概率敏感性分析,得到以下結(jié)論:
(1)葉身最大等效應力靜強度可靠度R=1.0,葉片0%葉高截面動強度可靠度R=0.98,葉片組前6節(jié)徑1階的振動可靠度R=1.0;同時,考慮強度和振動失效模式的情況下,葉片設計的可靠度R=1.0×0.98×1.0=0.98,未能達到99.73%的要求(±3σ準則);
(2)可靠性靈敏度分析結(jié)果表明,材料密度分散性對靜強度和振動可靠度影響最為明顯,工程實際中,要對材料密度分散性進行嚴格控制。

