方差輾轉(zhuǎn)的軟集參數(shù)約簡算法*

林連海,田立勤,2,蔡銘楷,李升宏

(1.青海師范大學計算機學院,青海 西寧 810008;2.華北科技學院計算機學院,河北 廊坊 065201)

1 引言

隨著科技的發(fā)展，大數(shù)據(jù)時代的到來，人們需要研究的數(shù)據(jù)關(guān)系變得更復雜，對系統(tǒng)的要求也越來越高。不論是在管理科學、社會科學還是工程應用中，都存在著諸多不確定的因素以及不確定的問題，若使用傳統(tǒng)的定量分析來處理這種不確定性問題，常常得不到想要的效果。最初，學者們利用概率論來研究數(shù)據(jù)的不確定性，但概率論不易直接用于決策中，需要對其進行一定的拓展。在此之后，各國學者考慮到現(xiàn)實世界的環(huán)境，提出了各種處理不確定問題的理論，較為經(jīng)典的理論有模糊集[1]和粗糙集[2]，這2個理論都可以看成經(jīng)典集合論上的一個延拓。由于這2個理論具備一定的局限[3]，1999年Molodtov提出了軟集[4]，隨后學者們對其展開了研究，規(guī)定了軟集的運算規(guī)則，創(chuàng)建了軟集的多種形式[5 - 7]，并將軟集用于現(xiàn)實決策中[8,9]。近年來，模糊軟集的概念和運用正被進一步推廣[10,11]。

軟集參數(shù)約簡的定義經(jīng)歷了諸多變化，文獻[8]將軟集理論用于決策，并進行了軟集的參數(shù)約簡，文獻[12]對其參數(shù)約簡方法進行了改進，直到文獻[13]提出關(guān)于軟集的常規(guī)約簡NPR(Normal Parameter Reduction)的概念，并提出了參數(shù)約簡的一種可行方法。

軟集參數(shù)約簡的方法有很多種，經(jīng)典的有：NPR算法、NENPR(New Efficient Normal Parameter Reduction)算法[14]、0-1線性規(guī)劃(0-1 Linear Programming)算法[15]、基于群體智能算法的粒子群約簡算法[16]、基于去重思想的約簡算法[17]和基于局部搜索的算法[18]等。

而概率論的誕生可追溯到16世紀，它是研究自然和人類社會中隨機現(xiàn)象的規(guī)律的數(shù)學分支，目前廣泛應用于自然科學、經(jīng)濟學、醫(yī)學、工程、金融保險甚至人文科學中。人們最早用于處理不確定數(shù)據(jù)的理論就是概率論。

本文將概率論和軟集進行結(jié)合，將方差的概念和性質(zhì)用于軟集的參數(shù)約簡問題之中，提出了適用于大數(shù)據(jù)背景下的約簡算法——方差輾轉(zhuǎn)法，用以解決軟集約簡參數(shù)的問題。

2 基本概念

定義1[13]設集合U={u1,u2,…,un}，集合E={e1,e2,…,em}，如果映射F能將集合E映射到全集U的冪集中，則稱(F,E)是在全集U上的1個軟集。其中，E一般稱為屬性集或元素集，而U一般稱為全集，實際背景下，E一般是U的屬性描述，為了區(qū)別于集合論中全集的概念，本文給U取了1個別名，稱其為物集。因此，軟集(F,E)可以看成是某個屬性與具備這個屬性的物集的子集的對應關(guān)系。如，對于e1，如果U中具備這個屬性的元素有u1,u3,u5，則F(e1)={u1,u3,u5}。我們通常也用F(u,e)=1或F(u,e)=0來表示u是或不是F(e)的元素，因此1個軟集可以用1個二值矩陣進行表示(示例見后文表1)。

定義2[15]定義物集元素u的支持集supp(u)為集合{e∈E|F(u,e)=1}。u的支持集的基數(shù)記為σE(u)，σE(u)=|supp(u)|=∑e∈EF(u,e)。當E為屬性集全集時，對應于表格中1行的和。

定義3[13]對于軟集(F,E)，設R?E且R≠?，若R滿足：

σE-R(u1)=σE-R(u2)=…=σE-R(un)

則稱R是軟集(F,E)的1個常規(guī)約簡。我們稱E-R是可約簡集。在所有常規(guī)約簡中，使可約簡集基數(shù)最大的常規(guī)約簡稱為最佳常規(guī)約簡，記為Rmax，對應的可約簡集稱為最佳可約簡集。

定義4約簡稠密度ρ=|E-Rmax|/|E|,即最佳可約簡集的基數(shù)與總屬性集的基數(shù)的比值。

定義5設軟集(F,E)的屬性集E={e1,e2,…,em}，A?E且A≠?，定義行和的集合：SA={σA(u1),σA(u2),…,σA(un)}。

3 概率論與軟集

由于概率論在諸多資料中都能參考，在此不加證明地給出以下定義和引理，并定義軟期望和軟方差，給出概率論與軟集結(jié)合得出的一些結(jié)論。

定義6(期望) 設X為1個離散型隨機變量，X的分布列給出了隨機變量X的所有可能取值及概率，則X的期望就是X所有可能的取值相對于當前取值概率的加權(quán)平均，記為E(X)。期望反映了隨機變量的平均取值大小。

定義7(軟期望) 將期望與軟集結(jié)合給出此定義。對于軟集的屬性集E={e1,e,…,em}，A?E且A≠?，將其行和SA視為隨機變量，SA的期望E(SA)稱為軟集(F,E)在屬性集A下的軟期望。軟期望用于描述物集在屬性集A下的支持集的平均大小。結(jié)合期望和軟集的常規(guī)約簡的定義，若1個屬性集是可約簡的，則其每1個物集元素的支持集大小都是相同的，對應于矩陣則表示其行和是相等的。

定義8(方差) 方差定義為var(X)=E[(X-E(X))2]。方差提供了隨機變量X在其期望周圍分散程度的1個測度。

定義9(軟方差) 將方差和軟集結(jié)合給出此定義。對于軟集(F,E)，令A?E且A≠?，將其行和SA視為隨機變量，其方差var(SA)稱為軟集(F,E)在屬性集A下的軟方差。軟方差用于描述物集在屬性集A下的支持集大小的離散程度。根據(jù)方差的定義，可知當軟方差為0時，SA中的元素是全相等的，即屬性集A是可約簡集，E-A是1個常規(guī)約簡。可見，軟方差能用于描述1個屬性集是最佳可約簡集的子集的可能性大小：軟方差越大，則該屬性集是可約簡集的可能性越小。

定義10(0-1分布) 對于1個事件而言，只有2種結(jié)果，當其發(fā)生的概率為p，而不發(fā)生的概率為1-p時，我們稱其服從0-1分布，且各屬性之間是獨立的(實際上，可約簡集中的屬性不是獨立的，這里主要是為了方便討論而簡化了模型)。

引理1設Qn為n個獨立的隨機變量X1,X2,…,Xn的和所構(gòu)成的序列，定義：

Qn=X1+X2+…+Xn

則由獨立性有以下關(guān)系：

var(Qn)=var(X1)+var(X2)+…+var(Xn)

引理2var(X)=var(X+k)，k為常數(shù)。

根據(jù)上述理論，可推導得出以下結(jié)論：

定理1假設軟集(F,E)的每個屬性之間是完全獨立的，A?E，B?A，即A是1個屬性集，B是A的1個真子集，則能推導出var(SA)≥var(SB)。換言之，若軟集(F,E)的每個屬性之間是完全獨立的，從屬性集中隨機選取的元素越多，那么對應的軟方差也就越大。

證明由于B?A，設A-B=C，根據(jù)引理2，有：

var(SA)-var(SB)=var(SC)

又方差是不小于0的，故

var(SA)-var(SB)≥0

得到結(jié)論。

□

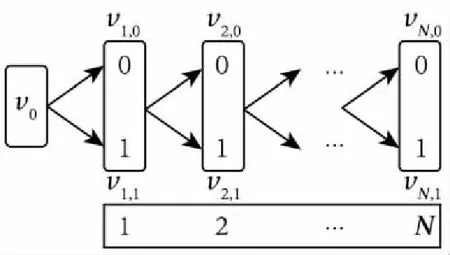
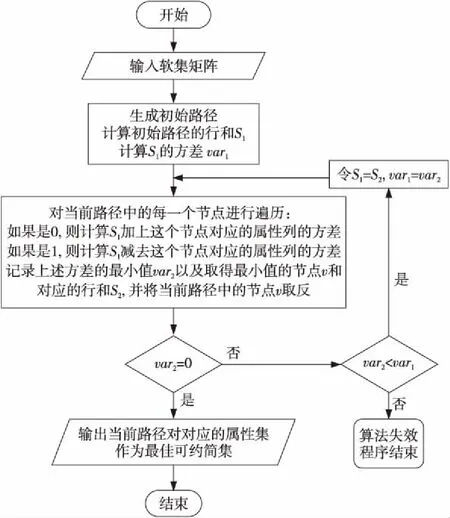
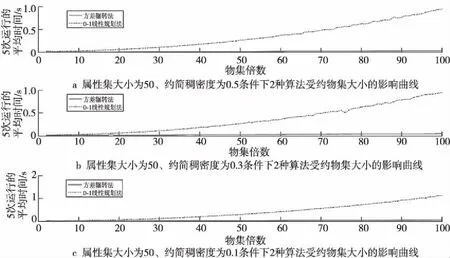
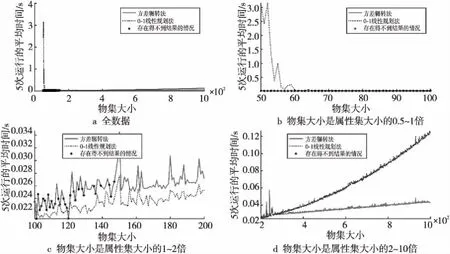
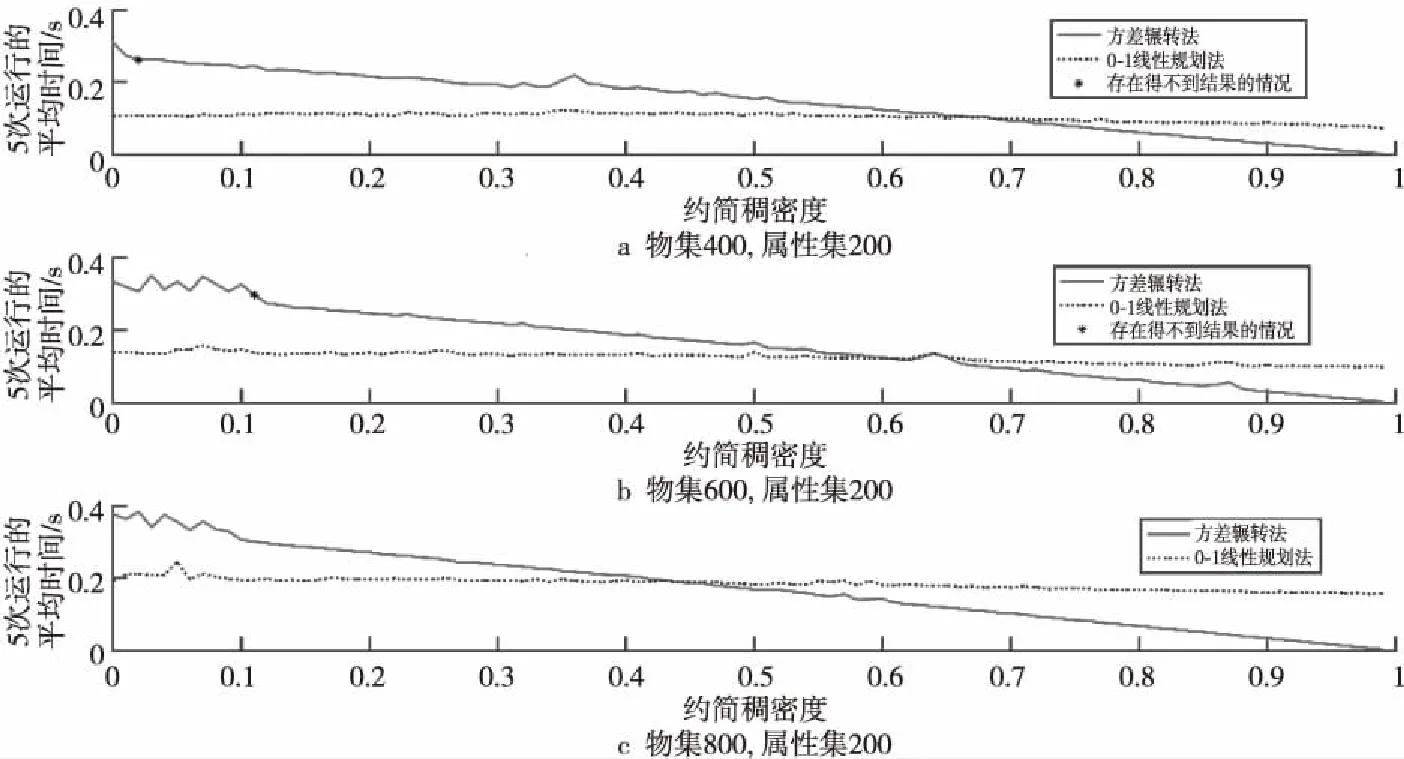
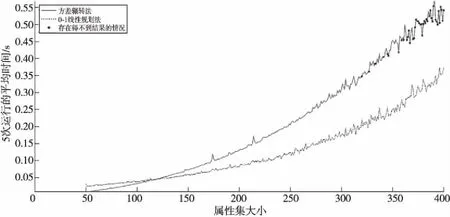
定理2設A為可約簡集，A′為從A中減少1個元素e的集合，當元素e對應F(ui,e)不是全0或全1時,i=1,2,…,n，有var(SA)

證明設隨機變量Y1,Y2,…,Yn服從于0-1分布，對應于取自可約簡集中的n個屬性，記Y為其和所構(gòu)成的序列，對應于軟集中的行和，有var(Y)=0，且對于任意物集元素u都有:

Y1+Y2+…+Yn=E(Y)

定義Qn、Pn如下：

Qn=Y1+Y2+…+Yn

Pn=Y1+Y2+…+Yt-1+Yt+1+…+Yn

即Pn為Qn中去除1個屬性后的n-1個獨立分布的聯(lián)合分布，可得到Pn實際是服從E(Y)-Yt分布的，即var(Pn)=var(E(Y)-Yt)，據(jù)引理2有：

var(E(Y)-Yt)=

var((-Yt)+E(Y))=var(-Yt)

由定義7知var(-Yt)=var(Yt)。綜上，即從約簡集中刪除1個屬性后，其所得集合的軟方差會等于被刪除的屬性本身的方差，由于可約簡集的方差為0，當被刪除的屬性不是全0或全1的屬性(也就是方差不為0)時，var(Pn)會大于var(Qn)。

□

注：上述理論是在大樣本情況下的，只有在樣本數(shù)足夠大的時候，方差和期望才有意義。后文算法思想也是在大樣本的條件下討論。

4 方差輾轉(zhuǎn)法

當今世界對于數(shù)據(jù)的獲取是相對容易的，各公司、機構(gòu)的數(shù)據(jù)庫中，通常都有成千上萬條數(shù)據(jù)，因此可以認為軟集矩陣在某個屬性上是服從0-1分布的。本文將貪心算法、概率論與軟集結(jié)合，給出一個在大數(shù)據(jù)背景下使用的軟集參數(shù)約簡算法——方差輾轉(zhuǎn)法。

4.1 算法思想

假設軟集(F,E)中所有的屬性之間都是獨立的，設一個任意的可約簡集表示為Xr={Xr1,Xr2,…,Xrq}，再設任意的最佳常規(guī)約簡的子集Xm={Xm1,Xm2,…,Xmw}，則屬性集的任意冪集可寫成E′=Xr+Xm，由于Xr可約簡，知SE′=S(Xm+Xr)=SXm+Kr(Kr為常數(shù))，據(jù)定理1，如果屬性集變大，對應的行和的集合SE′的方差會增加。即有以下2個結(jié)論：

(1)在Xm中，如果刪除1個屬性，SE′的方差會減少。

(2)在Xr中，如果刪除1個屬性，SE′的方差會增加。

綜上可以得到這樣1個結(jié)論：在1個屬性集中，如果刪除1個屬性，得到的剩余屬性集的軟方差如果變小了，那么這個屬性很可能是約簡集中的屬性。考慮極限情況，當樣本數(shù)量足夠多時，在1個屬性集中如果刪除1個屬性，軟方差變大的一定是最佳常規(guī)約簡中的屬性，而軟方差變小的一定是最佳可約簡集中的屬性。

另外，從定理1可以看出，當var(SC)等于0時，有var(SA)=var(SB)，也就是說對任意的屬性集，從中增加或刪除軟方差為0的屬性集不會對整體的軟方差有任何影響。當SC中僅有1個屬性的時候，即屬性為全0或全1的屬性時，是需要特殊處理的，需要將這種屬性包含到最佳可約簡集中。

4.2 路徑

參照二進制蟻群算法中的概念[19]，給出如下定義。

設有向圖G=(V,I)，頂點集為V，邊集為I，其中,V={v0,v1,0,v2,0,v2,1,…,vN-1,0,vN-1,1,vN,0,vN,1},v0表示起始頂點，vi,0和vi,1表示二進制碼串中bi位取0或取1的頂點。對軟集而言，N表示屬性集個數(shù)，設軟集的屬性集為E={e1,e2,…,em}，bi位取0表示當前屬性集不包含ei，取1表示包含ei。如圖1所示，為了表示方便，將vi,0與vi,1合并表示。我們將這樣表示的1個0/1二進制碼串稱為1條路徑。

在此結(jié)合軟集的參數(shù)約簡給出解釋：對于1個物集大小為n，屬性集大小為m的軟集(對應的二值矩陣是n×m規(guī)模的)，構(gòu)建1個長度為m的二進制串，表示1條路徑，同時，用這條路徑表示1個候選的可約簡集。該二進制串上的1個0/1值被稱為路徑的1個節(jié)點，每1個節(jié)點只能取0或者1，當?shù)趉個節(jié)點取1時，表示當前的候選可約簡集包含第k個屬性，這樣就可以用1個二進制串來表示軟集的1個候選可約簡集。

例如，設軟集的物集大小為5，屬性集大小為6，假設其第1、3、4個屬性元素構(gòu)成了1個可約簡集，那么這個可約簡集對應的路徑就是[1,0,1,1,0,0]。

Figure 1 Schematic of the path圖1 路徑示意圖

4.3 算法實現(xiàn)步驟

步驟1初始化路徑L，使其節(jié)點取值全為1。

步驟2計算路徑L對應屬性集子集的軟方差var1。

步驟3對路徑L進行遍歷，對所有取值為1的節(jié)點做如下操作：從L中刪除該節(jié)點(即將碼串中的對應位置設為0)，計算對應的軟方差，還原路徑L(取消刪除操作)。

步驟4記錄步驟3得到的軟方差的最小值var2，以及其對應的節(jié)點位置。

步驟5var2如果為0，則從路徑L中刪除步驟4得到的節(jié)點，此時L對應的屬性集即為最佳可約簡集，最后計算并返回最佳常規(guī)約簡集，結(jié)束算法。

如果var2>var1，則說明當前已經(jīng)是方差輾轉(zhuǎn)法能得到的最優(yōu)結(jié)果，方差輾轉(zhuǎn)法失效，退出算法。

如果var2

4.4 現(xiàn)實背景下的改進

上述算法在執(zhí)行的時候，經(jīng)常可能陷入局部最優(yōu)解，這通常是由于樣本數(shù)量不夠大，運用概率統(tǒng)計中的理論時會產(chǎn)生一定的誤差，因此算法需要有一定的容錯率。在此進行如下考慮：在算法執(zhí)行的初期，矩陣中包含許多相似程度較大的屬性列，在這樣的情況下，方差輾轉(zhuǎn)法很可能會錯誤地刪除可約簡屬性對應的路徑節(jié)點。假設方差輾轉(zhuǎn)算法執(zhí)行結(jié)束，算法失效，沒有得到結(jié)果，這時記錄的路徑中實際只是少了最初刪除的這個節(jié)點時，我們希望能將一開始誤刪除的節(jié)點重新加入到路徑中，故考慮增加節(jié)點的方法。

由定理2可知：如果可約簡集中減少1個屬性，軟方差一定會增加。根據(jù)這個結(jié)論可以推出：對1個可約簡集的真子集，增加1個不屬于這個真子集的可約簡屬性，軟集在這個真子集上的軟方差一定會縮小，因此將步驟3修改如下：

步驟3對路徑L進行遍歷，對每1個節(jié)點進行如下操作：取反(即如果是1則改為0，如果是0改為1)，計算軟方差，還原路徑(取消取反操作)。

4.5 算法流程圖

方差輾轉(zhuǎn)法流程圖如圖2所示。

Figure 2 Flow chart of variance toss algorithm圖2 方差輾轉(zhuǎn)法流程圖

4.6 時間復雜度分析

假設軟集的矩陣規(guī)模是n×m，則對路徑進行1次遍歷的時間復雜度可分成2部分：1部分是計算方差，其時間復雜度和物集大小n成正比，即O(n)；另1部分，每次迭代要計算當前路徑對應的屬性集的行和，這個操作的時間復雜度也是O(n)(在程序?qū)崿F(xiàn)時，先求出未操作前的行和，每次只需從這個行和中減去或加上軟集矩陣的1列即可)，每次迭代需求方差m次，故1次迭代的時間復雜度為O(m×(n+n))=O(mn)。

在沒有修改步驟3之前，迭代次數(shù)不會超過m，修改步驟3后，雖然不能確定迭代次數(shù)，但是其軟方差是在不斷減小，可以認為其不會超過2m(在實驗時，對于1個已刪除節(jié)點，后期可能會再加入可約簡路徑，但是沒有出現(xiàn)再次刪除的情況)。故整個算法的時間復雜度為O(m2n)。

而0-1線性規(guī)劃是整數(shù)規(guī)劃的一種，屬于NP難問題，雖然隨著運籌學的發(fā)展，出現(xiàn)了許多優(yōu)化的算法[20]，但這些優(yōu)化依舊不能使0-1線性規(guī)劃問題在多項式時間內(nèi)計算出結(jié)果。

由此可見，從時間復雜度上來說，方差輾轉(zhuǎn)法優(yōu)于0-1線性規(guī)劃法。

5 實驗

為了說明方差輾轉(zhuǎn)法的計算過程，將文獻[17]中給出的軟集數(shù)據(jù)作為示例，使用方差輾轉(zhuǎn)法進行參數(shù)約簡。

5.1 實驗數(shù)據(jù)

實驗數(shù)據(jù)如表1所示，數(shù)據(jù)規(guī)模為35×16，表1中每1列對應軟集中的1個屬性元素，每1行對應軟集中的1個物集元素。

5.2 實驗結(jié)果

對表1中的軟集使用方差輾轉(zhuǎn)法，計算過程如表2所示。

6 算法對比及分析

第5節(jié)使用方差輾轉(zhuǎn)法進行了1個簡單的實驗，展示了算法的運行具體流程，在本節(jié)將使用大規(guī)模的隨機數(shù)據(jù)進行實驗，以比較2種算法的效率以及準確度。

數(shù)據(jù)測試的運行環(huán)境都是MacBook Air(13-inch,2017)，使用的編程軟件是Matlab R2017b，運用Matlab中的隨機數(shù)生成軟集矩陣進行實驗。本文共給出了4個數(shù)據(jù)測試結(jié)果：物集倍數(shù)(物集大小與屬性集大小的比值)對運行效率的影響曲線、物集大小對運行效率的影響曲線、約簡稠密度大小對運行效率的影響曲線和屬性集大小對運行效率的影響曲線。實驗結(jié)果表明，方差輾轉(zhuǎn)法在大數(shù)據(jù)背景下，運算效率高于0-1線性規(guī)劃法。

6.1 物集倍數(shù)的影響

實驗使用的數(shù)據(jù)是由Matlab隨機生成的， 其中物集大小從屬性集大小的3倍到100倍變化，每次隨機5組數(shù)據(jù)求平均值，共1 470組隨機數(shù)據(jù)。 實驗結(jié)果如圖3所示。

可以看出，物集的倍數(shù)越高，方差輾轉(zhuǎn)法的運算效率越高，運算時間相比于0-1線性規(guī)劃算法有大幅度縮短。

根據(jù)實驗結(jié)果可以計算出，當物集大小是屬性集大小的100倍,約簡稠密度 (見定義4)為0.1時，0-1線性規(guī)劃的運行時間大約是方差輾轉(zhuǎn)法的20倍，而約簡稠密度是0.5時，前者大約是后者的30倍。

大數(shù)據(jù)時代，數(shù)據(jù)庫中1個有50多個字段的表通常會有上萬條記錄，即物集大小是屬性集大小的百倍甚至以上時，本文算法的時間效率比0-1線性規(guī)劃法的高很多。

6.2 物集大小的影響

實驗使用的是屬性集大小為100、約簡稠密度為0.5的隨機數(shù)據(jù)，物集大小從50～1 000遞增，共4 755組隨機數(shù)據(jù)。實驗結(jié)果如圖4所示，其中，圖4a是全數(shù)據(jù)的實驗結(jié)果，圖4b～圖4d是對全數(shù)據(jù)某一部分的放大。

Table 1 Example of soft set matrix表1 示例的軟集矩陣

Table 2 Example calculation procedure表2 示例的計算過程

從圖4a來看，方差輾轉(zhuǎn)法和0-1線性規(guī)劃法的運算效率相差不大，在同1個數(shù)量級。

Figure 3 Influence of the multiple of the universal set size圖3 物集倍數(shù)的影響

Figure 4 Influence of universal set size圖4 物集大小的影響

圖4b是物集大小是屬性集大小的0.5～1倍時的實驗結(jié)果。在這種情況下，方差輾轉(zhuǎn)法幾乎得不到結(jié)果。但同時，0-1線性規(guī)劃法也會出現(xiàn)很難得到結(jié)果的情況(雖然從統(tǒng)計圖上看有運行時間結(jié)果，這是因為程序中對0-1線性規(guī)劃設計了時間限制，當超出這個時間時，算法會直接結(jié)束),特別是屬性集大小正好是物集的2倍時，0-1線性規(guī)劃法經(jīng)常在可接受時間內(nèi)得不出結(jié)果。例如，對于規(guī)模為100×200的隨機軟集，0-1線性規(guī)劃法在MacBook Air (13-inch,2017上)連續(xù)運行2個小時(Matlab默認最大運行時間)，依舊得不到結(jié)果。

從圖4c可以看出,隨著物集大小的增加，方差輾轉(zhuǎn)法逐漸生效，物集大小達到屬性集大小的2倍后，沒有出現(xiàn)過約簡失敗的情況。

圖4d和圖3結(jié)論一致，說明在大數(shù)據(jù)背景下，方差輾轉(zhuǎn)法是優(yōu)于0-1線性規(guī)劃法的。

6.3 約簡稠密度大小的影響

實驗使用的屬性集大小為200的隨機數(shù)據(jù)，選取物集的大小分別為400，600和800，統(tǒng)計約簡稠密度對算法效率的影響。實驗結(jié)果如圖5所示。

從圖5可以看出，約簡稠密度對方差輾轉(zhuǎn)法的影響很大，但是對0-1線性規(guī)劃法幾乎沒有影響。同時從圖5a和圖5b可看出，方差輾轉(zhuǎn)法存在著缺點：即使當物集足夠大時，如果約簡屬性不夠多，也可能出現(xiàn)約簡失敗的情況(實際上在圖5a和圖5b中，分別有1 500次測試，各出現(xiàn)了1次約簡失敗的情況，圖5c中沒有出現(xiàn)約簡失敗，其實在約簡稠密度極低的時候，參數(shù)約簡的實際意義就不大了)，這說明算法仍有需要改進的地方。如果約簡稠密度足夠高，方差輾轉(zhuǎn)法會優(yōu)于0-1線性規(guī)劃法，并且從圖5中能夠看出，方差輾轉(zhuǎn)法的運行時間與約簡稠密度基本成反比。

6.4 屬性集大小的影響

實驗使用的數(shù)據(jù)為：屬性集大小從50～400遞增，共1 755組隨機數(shù)據(jù)。實驗結(jié)果如圖6所示。

從圖6中可以看出，方差輾轉(zhuǎn)法和0-1線性規(guī)劃法的運行時間相差不是很大，在屬性集較小時，方差輾轉(zhuǎn)法優(yōu)于0-1線性規(guī)劃法，但是當屬性集增大時，方差輾轉(zhuǎn)法運行時間就會超過0-1線性規(guī)劃法的，屬性集繼續(xù)增大，方差輾轉(zhuǎn)法會出現(xiàn)約簡失敗。

Figure 5 Influence of reduction density圖5 約簡稠密度的影響

Figure 6 Influence of attribute set size圖6 屬性集大小的影響

7 結(jié)束語

本文將軟集和概率論結(jié)合，提出了一個應用于大數(shù)據(jù)背景下的軟集參數(shù)約簡算法——方差輾轉(zhuǎn)法，對于n行m列的軟集矩陣，此算法的時間復雜度是O(m2n)。

實驗表明，在物集足夠大的時候，方差輾轉(zhuǎn)法的效率超過0-1線性規(guī)劃法的效率。算法的實現(xiàn)環(huán)境要求簡單，不需要依賴于Matlab等特定的運行環(huán)境；運行機制明了，實現(xiàn)起來極為簡單；實現(xiàn)過程中，大部分運算時間都用在了向量計算上，這非常利于并行計算的設計，效率還有進一步提升的空間。

當然方差輾轉(zhuǎn)法還有許多需要完善的地方，例如概率模型的建立以及模型在概率論上的理論解釋等等。概率論與軟集的結(jié)合以及概率論與貪心算法的結(jié)合都是本文的創(chuàng)新點，同時也是值得研究的方向。