基于改進ACF算法的道路行人檢測算法研究

王衍，陳鏡任，馮宇慶

（1.重慶珞璜港務有限公司，重慶402260；2.武漢理工大學計算機科學與技術學院，武漢430063；3.武漢民政職業學院，武漢430070）

0 引言

港口行人、車輛眾多，對港口行人的運動軌跡進行跟蹤對于港口作業安全具有很大意義。

行人檢測是行人運動軌跡預測的基礎，要想對行人運動進行分析，并預測其接下來的運動趨勢，首先就必須要檢測出初始幀中行人存在的具體位置。行人檢測技術發展至今已經取得了一定的效果，但依然存在誤檢漏檢的情況，給行人檢測帶來不小挑戰[1-2]。

行人檢測的目的是判斷圖像中是否存在行人，并找到其具體位置。行人檢測算法主要有基于背景建模、基于深度學習、基于機器學習這三類。

基于背景建模的方法要求攝像頭須是固定不動的，同時，算法只能將運動的目標與背景進行分離，而不能判斷出運動中的前景目標的類別，其適用的場景受到限制。基于深度學習的方法運算復雜度較大，對硬件要求較高，應用落地性有待提升。基于機器學習的方法可以應對靜態和運動的攝像頭所拍攝到的視頻圖像，且對硬件要求不高，因此本文選用基于機器學習的行人檢測方法進行研究。該方法的基本框架如圖1所示。

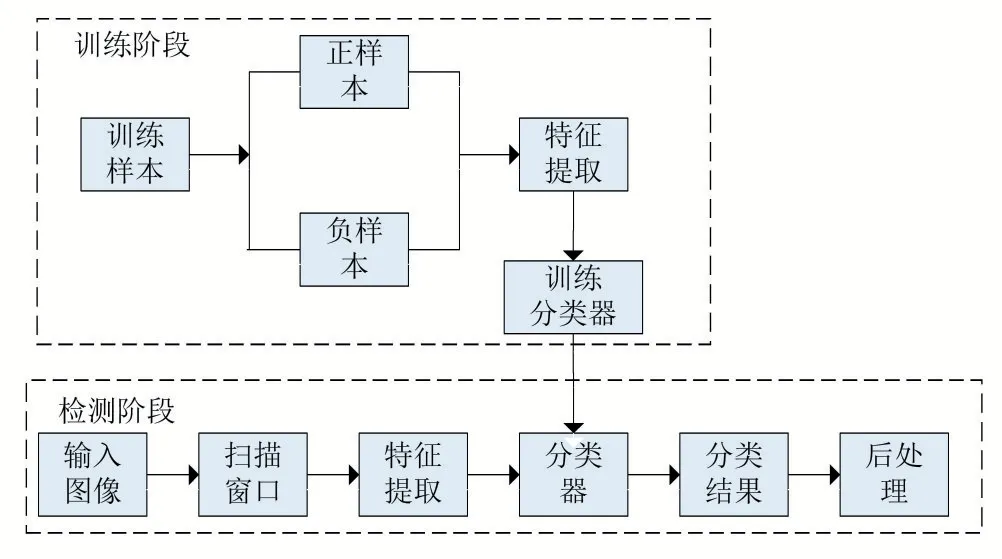
圖1行人檢測算法框架

1 基于改進ACF的行人檢測算法

ACF[1]是一種基于機器學習的、性能較為不錯的行人檢測算法。ACF采用聚合通道特征作為行人特征，采用AdaBoost算法作為分類器，經過訓練得到了檢測性能較好的行人檢測器。圖2為ACF行人檢測算法流程。

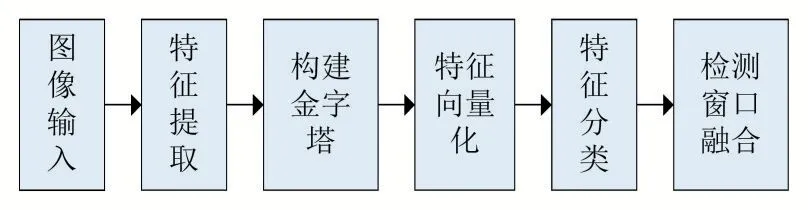
圖2 ACF行人檢測算法流程

1.1 聚合通道特征

聚合通道特征中包含了三種特征通道，其中，顏色通道有三個，梯度幅值通道有一個，梯度方向通道有六個[3-4]。

（1）顏色特征：行人的顏色特征主要表現在行人的衣著上，根據顏色特征可以將穿不同顏色衣服的行人檢測出來。用于行人檢測的主要顏色特征有：LUV、RGB、HSV。

（2）HOG特征：HOG特征能夠描述圖像的局部梯度方向和梯度強度分布，能夠在邊緣位置未知時，利用邊緣方向的分布來表示目標的外形輪廓。

1.2 構造特征金字塔

傳統的構建特征金字塔的方法較為繁瑣，它將待檢測的圖像進行多尺度縮放，之后在所有的尺度上都要 提 取 特 征，按 照Cs=Ω( R( I,s) )計 算，而 忽 略 掉C=Ω(I)中包含的信息。

本文構建特征金字塔的方法是：將待檢測的圖像縮小為原來的1倍、2倍、4倍，然后計算這三個尺度上的特征，用已經計算出的三個尺度上的特征去估計其他尺度上的特征。具體思路為：令Is表示在尺度s上捕捉到的圖像I，R( )I,s表示用s重采樣得到的圖像I。在已經計算出C=Ω()I的情況下，用C在新尺度s上預測通道圖像Cs=Ω(Is)。采用如（1）式所示的特征近似的思路，這種近似處理簡便、相對準確，提升了構建金字塔的速度：

圖3為傳統特征金字塔與快速特征金字塔比較圖。

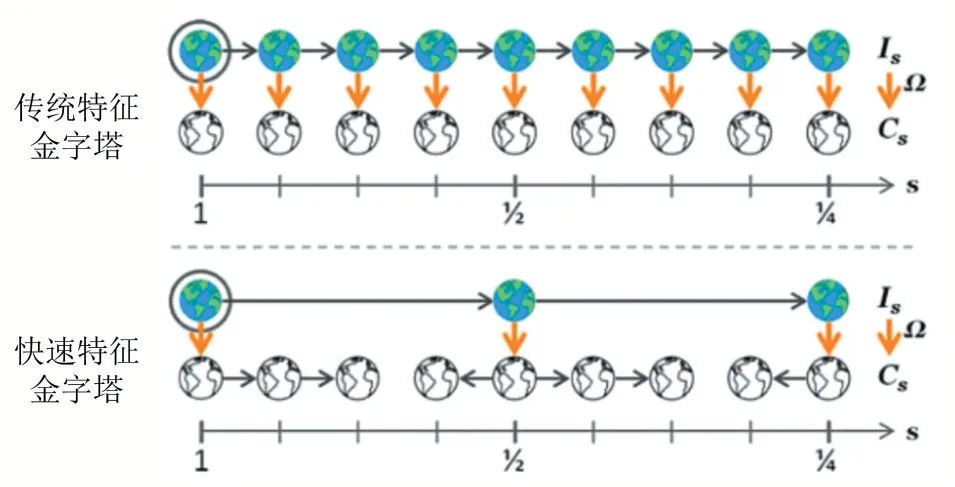
圖3傳統特征金字塔與快速特征金字塔比較

1.3 改進的AdaBoost

Kearns等人[5]于1988年在研究可能近似正確學習（Probably Approximately Correct Learning，PAC Learn?ing）時提出了Boosting問題，對于“能否將弱可學習視為強可學習”提出了疑問，而Schapire則在隨后對該問題作出了肯定的回答，并設計出了第一個Boosting算法。但Boosting算法的前提是要能夠預知弱分類器的錯誤率上限，這就使得其難以應用于實際問題中。后來，Freund等人發現在線分配問題與Boosting問題非常相似，于是他們在Boosting算法中引入了在線分配思想。即，將加權投票與在線分配問題相結合，得到了著名的AdaBoost算法。AdaBoost算法無需提前知道弱分類器的先驗知識，這一點促使其成為主流的分類算法，并在解決實際問題中取得了極大成功[6]。

（1）原始的AdaBoost及分析

原始的AdaBoost算法給定訓練樣本及其分類( x1,y1),…,( xn,yn)，其中xi∈X，yi∈Y={- 1,+1}。初始化樣本的權重D1(i)=1 n，即初始時，各個樣本權重相等。

分析經典的AdaBoost算法可知，對難度較大的樣本進行分類時，會使困難樣本的權重以非常快的速度增長，這樣就產生了“退化問題”。此外，AdaBoost易受噪聲干擾，執行效果依賴于弱分類器的選擇，且弱分類器訓練時間偏長。

（2）改進的AdaBoost

為了克服經典AdaBoost的上述缺點，可以修改弱分類器權重值αt的計算方法。新的計算方法為：

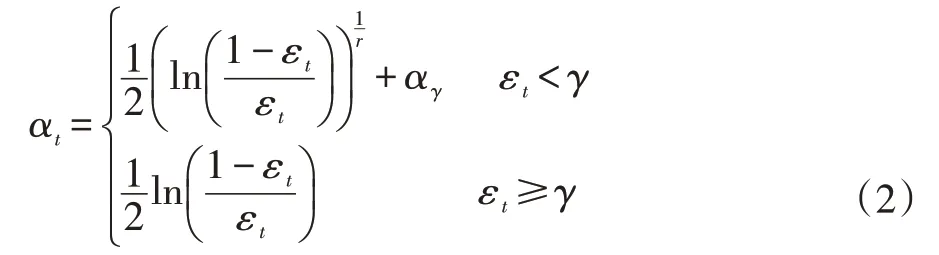
利用上式計算弱分類器權重值αt，防止任一樣本的經驗分布在某一階段中顯著增長。然而，在每一步更新經驗分布，經過幾次迭代之后，與其他樣本相比，那些被重復錯誤分類的樣本的概率權重的值會大大增加。因此，為每個樣本i=1,2,...n引入反向變量β()i和年齡變量life(i)。反變量β(i)的初始值為1，此時算法就按照經典AdaBoost算法處理樣本，即，當樣本被錯誤分類時，就增加其經驗分布，否則減小其經驗分布。如果的值是-1，則算法就按照逆AdaBoost處理樣本，即，當樣本被錯誤分類時，減小其經驗分布，否則增加其經驗分布。變量life(i)計算樣本i被按順序錯誤分類的次數，如果該數量超過閾值τ，則將β(i)的值反轉為-1。也就是說，被錯誤分類的樣本的權重會持續增長，直到迭代次數達到極限τ，然后開始減小。如果β(i)在被反轉為-1后，樣本在接下來的步驟中被正確分類，那么就將β(i)的值又反轉回1。

改進后的算法在經典AdaBoost和逆AdaBoost之間交替。通過將異常值的影響限制在經驗分布中，檢測并減少困難樣本的經驗概率，并在污染數據下執行更準確的分類，使得其性能更加穩定。

在第一階段采用上述權值更新方法，經過多輪訓練，獲得一個較為可靠的樣本分布wi(s)。接下來，在第二階段采用并行方法，提高訓練效率，在訓練中不再對樣本權值進行更新，而統一采用wi(s)。改進的Ada?Boost如下程序所示：

輸入：給定訓練集Z={( x1,y1),...,( xn,yn)}，其中xi∈X，yi∈Y={- 1,1}；

輸出：強分類器HT(x)

1參數初始化：設置年齡變量的閾值τ，界限閾值λ，魯棒參數r，令T=0；

2為每個樣本( x1,y1),i=1..n.初始化經驗分布D1(i)=1 n，反向變量β(i)=1，年齡變量life(i)=0；

3 repeat

4將T增加1；

5從訓練集Z中獲取帶有分布DT的自舉樣本ZT；

6使用自舉樣本ZT作為訓練集，訓練弱分類器hT:X→{- 1,1}；

7 按式（7）計算弱假設hT的加權錯誤率εt；

8按式（11）計算αT；

9按式（10）計算經驗分布；

10按式（11）計算階段T的強假設HT(x)

11 使用強假設HT(x)對訓練數據集Z={( x1,y1),...,( xn,yn)}進行分類；

12 if HT(x)將樣本( x1,y1)正確分類，即HT(xi) yi>0 then

13 令life(i)=0且β(i)=1；

14 else

15 使life(i)增加1；

16 if life(i)>τthen令β(i)=-1且life(i)=0；

17 end if；

18 until達到標準

1.4 改進的ACF算法框架

綜上所述，得到改進的ACF算法框架如圖4所示。

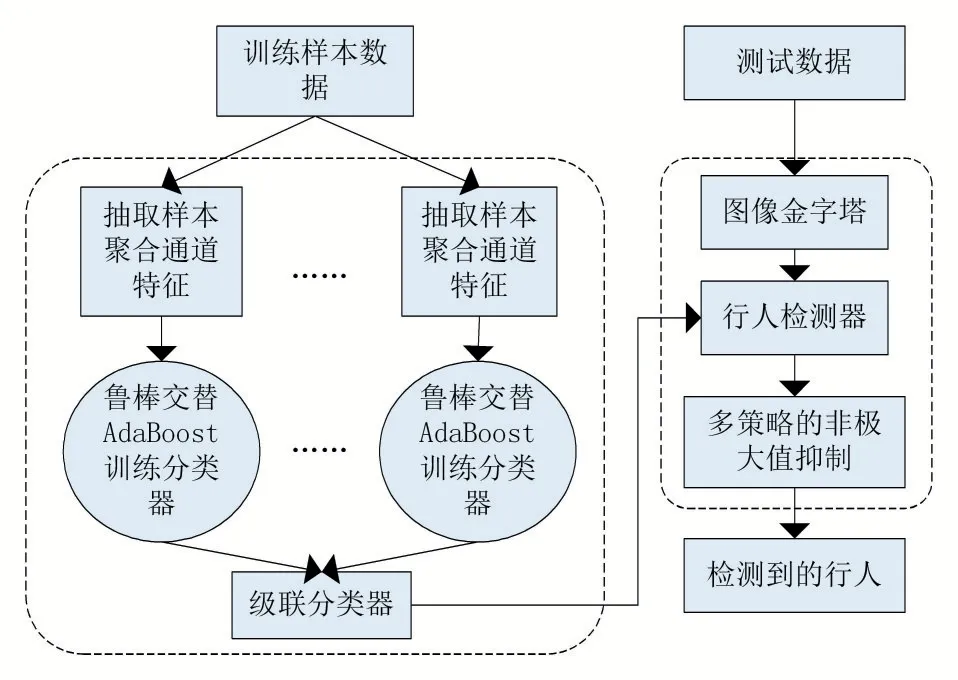
圖4改進的ACF行人檢測框架

2 實驗設計及分析

2.1 數據集

本文的訓練使用的數據來自INRIA數據集，訓練集里原本有614張行人圖片，一共1239個正樣本，樣本數偏少，只用這些數據進行訓練難以得到分辨能力更強的分類器，因此將原本的1239個正樣本經過鏡像翻轉，得到2478個正樣本，負樣本選自INRIA和Caltech。測試集選自INRIA測試集中的圖像和在校園內自采集的行人圖像，一共包含750張圖像，共673個正樣本，429個負樣本。

2.2 評價指標

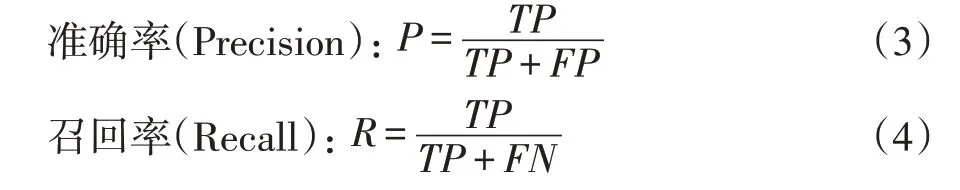
其中，真正例（True Positive，TP）：實際上是行人，被檢測成行人的圖像數。假正例（False Positive，FP）：實際上不是行人，被檢測成行人的圖像數。真反例（True Negative，TN）：實際上不是行人，被檢測成非行人的圖像數。假反例（False Negative，FN）：實際上是行人，被檢測成非行人的圖像數。

2.3 定量分析

通過在INRIA測試集中抽取的正樣本行人圖像和自采集的行人圖像組合而成的測試集上進行實驗，與同是基于機器學習的HOG+SVM算法、DPM算法、ACF算法進行比較，結果如表1所示。

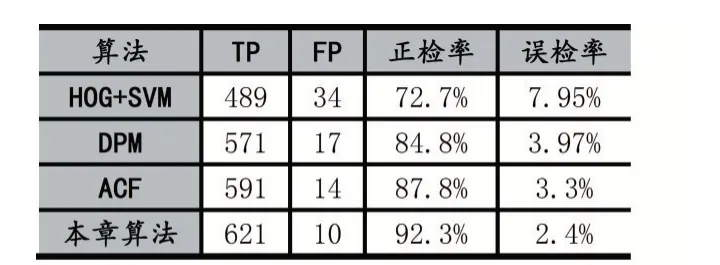
表2不同算法行人檢測結果比較

如表2所示，本文提出算法的正確檢出率為92.3%，相比于HOG+SVM、DPM、ACF有一定的升。

同時考慮準確率和召回率，以召回率（Recall）為橫坐標，以準確率（Precision）為縱坐標，得到P-R圖，P-R曲線圍成的面積就是檢測精度，即，P-R曲線圍成的面積越大，檢測的平均精度越高。如圖5所示，HOG+SVM檢測算法的P-R曲線在最下面，圍成的面積最小；DPM的P-R曲線比HOG+SVM圍成的面積要大；再上面是ACF；再上面是本文算法。本文算法的P-R曲線圍成的面積最大，說明其檢測的平均精度是最高的。

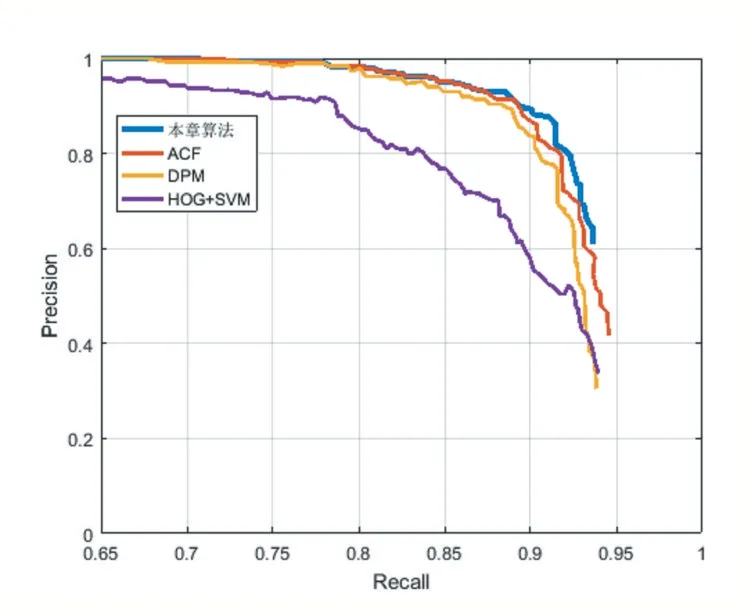
圖5各算法的P-R圖

3 結語

本文對ACF算法進行了改進。實驗表明，算法降低了誤檢率和漏檢率，檢測效果有一定提升。在未來的研究中，將研究提升算法對大幅形變的行人的檢測效果。