基于對稱破壞的子圖同構約束求解算法
徐周波,梁軒瑜,劉華東,2+,戴瑀君
(1.桂林電子科技大學 廣西可信軟件重點實驗室,廣西 桂林 541004; 2.桂林電子科技大學 機電工程學院,廣西 桂林 541004)
0 引 言
子圖同構問題是圖模式匹配[1]中的核心問題。求解子圖同構問題的方法一般分為2類。基于樹搜索的方法[2-5],該類算法通常在狀態空間表示(state space representation,SSR)中,采用基于回溯的深度優先搜索,結合啟發式信息,以增量的方式,不斷的在新狀態下檢查是否滿足子圖同構約束。該類算法的優點是不需要將所有狀態保留在內存中,其分配的最大狀態數與目標圖節點數呈正比關系;基于約束滿足問題(constraint satisfaction problem,CSP)求解的方法[6-9],該類算法利用圖中的屬性和結構信息,結合約束傳播、弧一致性等技術,迭代地在所有可能節點對中過濾掉一定不是解的節點對,最終留下的節點對即為所求解。該類算法優點是求解速度快,但是需要保留不滿足約束的節點對以避免被重新搜索,因此對內存的需求較多。
研究者們從不同的角度致力于提高子圖同構算法的求解效率并擴大問題求解規模,但子圖同構問題所面臨的組合復雜性問題,仍成為它們被廣泛應用的瓶頸[10]。大量研究致力于使用更多的鄰居關系來構建約束以減少搜索域,而忽略了重復解的問題。因此本文提出一種可避免解的重復搜索的子圖同構約束求解算法,結合對稱破壞思想,在求解過程中,利用對稱破壞約束來避免解的重復搜索。通過一些標準庫用例進行實驗分析,其結果表明,與傳統算法相比,本算法有效減少了重復解,提高了求解效率。
1 相關介紹
1.1 子圖同構及約束滿足問題
定義1 給定目標圖Gt=
子圖同構問題是指在目標圖中找到一個或所有與模式圖同構的子圖。本文的算法致力于求解所有與模式圖同構的子圖。
定義2 約束滿足問題定義為三元組
(1)X={x1,x2,…,xn} 為包含n個變量的有限集合;
(2)D={D(x1),D(x2),…,D(xn)} 為n個變量的值域;
(3)C={c1,c2,…,cm} 為約束集合,ci(xi1,xi2,…,xij)?Di1×Di2×…×Dij(i=1,2,…,m,1≤j≤n), 其中xil∈X(l=1,2,…,j),Dil為變量xil的域,稱ci為定義在變量集 {xi1,xi2,…,xij}?X上的j元約束。
CSP求解的目標是找到變量集X的全部實例化,使得約束集C中的所有約束均得到滿足。
將模式圖中的節點構成變量域X,目標圖中的節點構成值域D。 子圖同構的一般CSP模型表示如下:
(1)變量域:X=Vp;
(2)值域: ?xi∈Vp,Di=Vt;
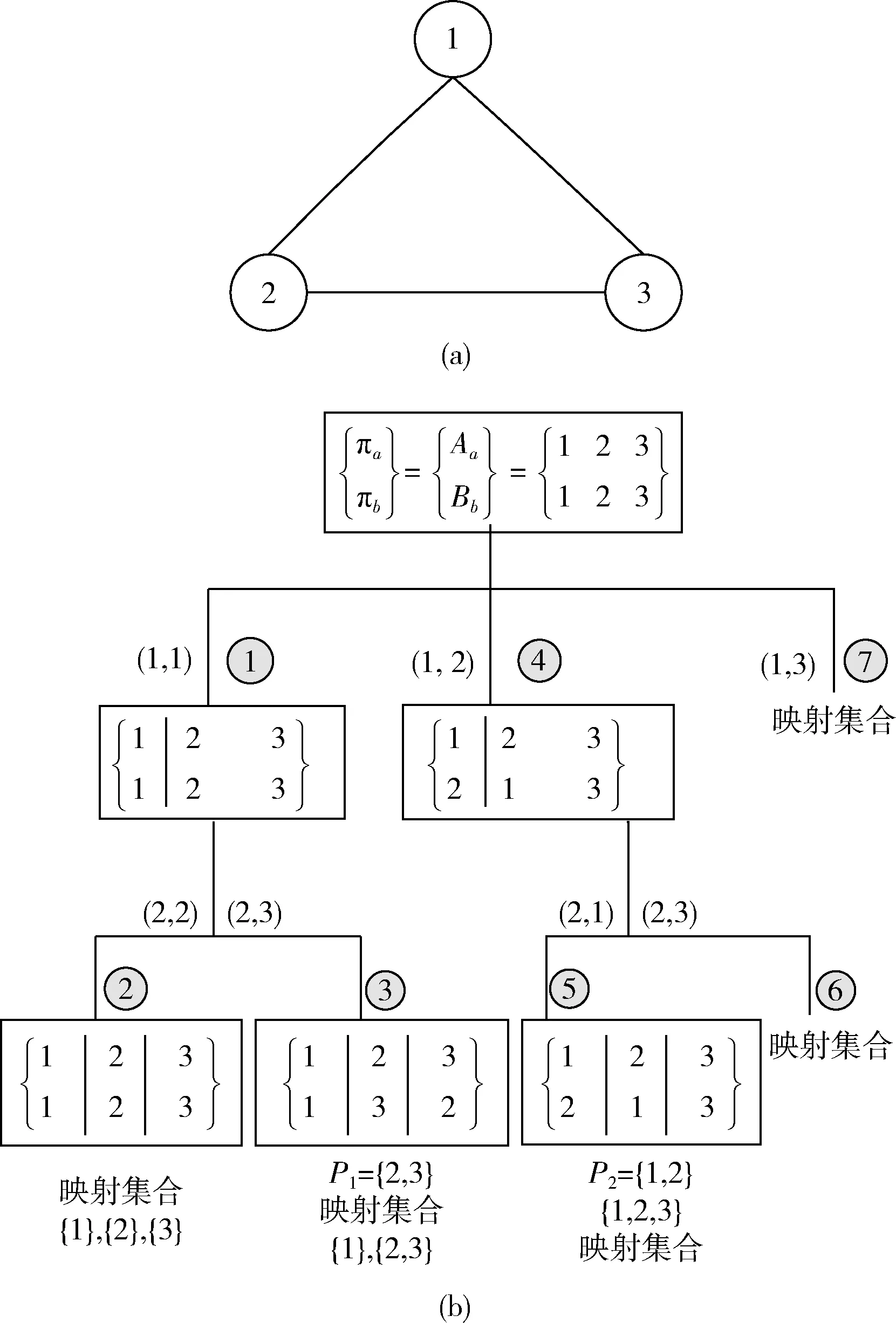
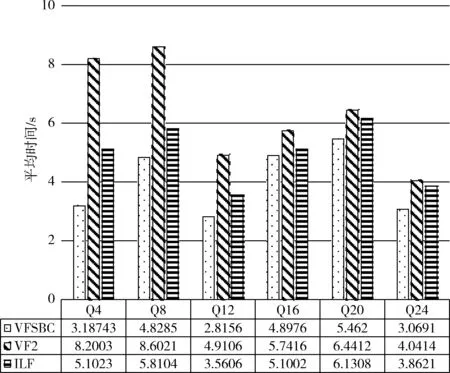
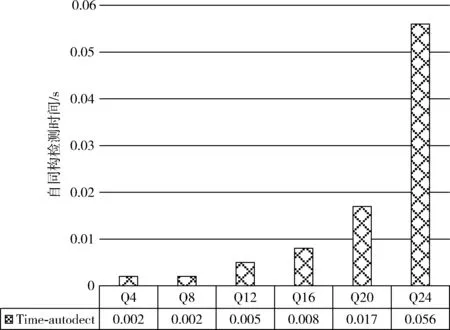
(3)約束域: ?i,j∈Gp(i 用置換來描述對稱性。In為包含1到n用于表示變量的整數集合,集合Sn表示In的所有置換,一個置換σ描述為向量 [1σ,2σ,…,nσ]。 定義3[11]給定i∈In和置換群G∈Sn,iσ為變量i經σ置換后對應的變量,則iG表示置換群G中i置換后對應的變量的集合:iG={iσ|σ∈G}。 定義4[11]給定i和置換群G,iG表示在置換群G中,能使節點i經置換σ不變的置換集:iG={σ∈G|iσ=i}。 CSP中的變量對稱指能使 (xi=j)ρ=(xiσ=j) 的置換,其中j∈D(xi),ρ為滿足解的變量-值對之間的雙射。例如,有如下約束滿足問題。變量集為 {1,2,3}, 每個變量的值域為 {0,1,2,3,4,5}, 約束為{x1+x2+x3=5}。 可以知道,該CSP的其中兩個解為 {x1=0,x2=2,x3=3} 和 {x1=2,x2=0,x3=3}, 即 [1σ,2σ,3σ]=[2,1,3], 在同樣的變量域和值域下,值0分配給變量x1或x2皆滿足該CSP解的條件,那么稱x1和x2為變量對稱的。在本文中考慮的是變量對稱。 將子圖同構約束求解與對稱破壞技術結合,應用于子圖同構CSP模型。首先通過檢測模式圖的自同構得到一系列置換,這些置換構成置換群。再對置換群進行群操作得到穩定鏈和陪集。最后,通過陪集生成節點間的字典序約束,構建子圖同構CSP模型并使用回溯算法對其求解。 圖的自同構指的是圖與自身的同構。Houbraken[12]檢測自同構的方法在迭代過程中存在保留大量冗余節點問題,針對此問題,本文在每次配對只記錄鄰居節點,然后根據當前記錄信息與其它節點比較,從而降低了匹配次數及內存占用。本文自同構的檢測方法,主要分為以下3個步驟。 步驟1 按節點的度將節點進行分類,將度相同的節點歸入同一單元。整個檢測過程依靠πa和πb兩個劃分,其中πa={A1|A2|…|Aa}, πb={A1|A2|…|Ab}, 每個劃分由不同單元構成。此時上下層單元數都為n,具有相同度節點的上層劃分單元與對應的下層劃分單元具有相同的標記。圖1(a)所示的模式圖,其自同構檢測過程如圖1(b)所示。在搜索樹頂部的初始劃分中,節點1,2和3由于度數相同,因此位于同一單元中。 圖1 自同構檢測過程 步驟2 當上層劃分單元Ai內的節點數量大于1時,將Ai內的每個節點依次與對應Bi內的所有節點進行組合配對。將當前配對的節點中,原屬于Ai的節點放入新建的上層劃分單元An+i中,原屬于Bi的節點放入新建的下層劃分單元Bn+i中。對于新建的An+i和新建的Bn+i內的節點,觀察其鄰接點,為鄰接點添加連接邊標記neibor,并記錄新建上層分區單元An+i內節點的鄰接點所屬單元標記。對每個鄰接點的所屬單元標記所對應的上層分區單元Ai和下層分區單元Bi內的節點進行分類,對于Ai內的節點:將有neibor標記的節點保留在該Ai內,將沒有neibor標記的節點從原所屬單元移入到新建的上層分區單元A2n+i中,同時記錄此新建A2n+i的單元標記并存入臨時標記集Nlabel中。同理對Bi內節點進行分類,但并不需要保存新建B2n+i的單元標記。如圖1(b)中步驟2(圓圈內的數字表示檢測步驟)所示,πa中節點1與πb中節點1配對,置入具有相同單元標記的上下兩個新單元中,其鄰接點節點2與節點3因具有neibor標記而保留在原單元內。檢查上層劃分與下層劃分內各單元,若上層單元Ai與下層單元Bi內的節點數量不一致,則向上回溯至重新選取節點配對,否則取臨時標記集合Nlabel內的單元標記,找到與此單元標記對應的上層分區單元Ai,重復步驟2。 步驟3 當上層劃分與下層劃分的每個單元均僅包含一個節點時,若上層劃分中的節點a與下層分區中的節點b的所屬單元標記相同,且上層劃分中的節點b與下層劃分中的節點a的所屬單元標記相同,則節點a和節點b構成一組生成置換。如圖1(b)中步驟3所示,得到一組生成置換P1=(2,3)。 一系列生成置換構成自同構群G, 此自同構群即為作用于圖中節點的置換群。在圖1所示例子中,自同構群由P1和P2構成。 剪枝是一種縮小搜索空間的群優化技術,用于刪除部分搜索樹。通過已檢測的生成置換構建映射集合,用于避免不必要的配對過程,同一映射集合內的節點可以映射到自身或集合內的其它節點。在圖1(b)所示步驟2中,得到映射集合 {1},{2},{3}。 通過P1更新映射集合為 {1},{2,3}。 由P2知,根據傳遞性,更新映射集合為{1,2,3}。在自同構檢測過程中,若配對的節點屬于同一映射集合,則刪除當前搜索分支。 子圖同構約束求解中,圖的自同構導致重復解。如何將檢測得到的自同構轉化為一種約束,是約束求解中減少重復解的關鍵點。本文引入Puget[11]的生成破壞對稱約束方法。首先通過置換群得到穩定鏈,其次利用穩定鏈求得陪集,最后,通過陪集生成字典序約束從而破壞對稱。 置換群G中的置換通過將節點交換到序列中的不同位置而作用于節點序列。對于未改變節點位置的置換,如定義4中iG所示,稱其為穩定。由穩定,穩定鏈定義為: ?i∈In,Gi={iGi-1|G0=G,Gi={σ∈G∶1σ=1∧…∧iσ=i}}。 由P1和P2可得置換群G為: {[1, 2, 3], [1, 3, 2], [2,1, 3]}。 陪集Ui定義為:Ui=iGi-1,Ui表示在置換群Gi-1中,節點i所能映射的節點集合。在圖1所示的例子中,U1={1,2},U2={2,3},U3={3}。 令r(j) 為能使j屬于Ui且不等于j的最大i, 若除了Uj之外沒有這樣的Ui使之滿足,則令r(j)=j, 由此可得對稱破壞約束: ?j∈In,r(j)≠j?xr(j) 在圖1所示的例子中,r(1)=1,r(2)=1,r(3)=2, 由此可得對稱破壞字典序約束為:x1 給定目標圖Gt= (1)變量域:X=Vp; (2)值域: ?xi∈Vp,Di=Vt; (3)約束域: 1)邊約束c(i,j): 如1.1節所述。 2)全不同alldiff約束:alldiff(x1,x2,…,xn)={(d1,d2,…,dn)|?di∈D(xi),?i≠j,di≠dj,i=1,2,…,n}。 3)度約束Ri: Ri={va∈Vt|deg(Gp,i)≤deg(Gt,va)}, 其中deg(Gp,i) 用于表示模式節點i的度, deg(Gt,va) 表示對應目標節點va的度。 5)對稱破壞約束SBC:根據2.2節的方法生成對稱破壞約束SBC。若變量受到alldiff約束的限制,那么最多可以用n-1個二元約束破壞CSP中的對稱解。這些約束構成了對稱性破壞約束SBC。 其中,alldiff約束用于在CSP求解中保證單射,限制一一對應的節點映射關系。Ri約束用于構造初始域,刪除不滿足此約束的變量值域。當模式節點和目標節點匹配時,只有目標節點的度大于或等于模式節點的度,才可能是導出子圖同構。NDC約束用于獲取更多的鄰居信息以減少值的范圍。選取不同k值效果不一,并不是k的值越大,效果越好,因為當圖的規模很大時,矩陣計算是非常耗時的。在本文中,最小的模式圖有4條邊,因此統一設k值為4。 算法主要分4個步驟,第一步為各變量賦初始值域,第二步為自同構檢測,第三步生成對稱破壞約束,第四步完成約束求解。給出偽代碼如下。 VFSBCAlgorithm:Gp=(Vp,Ep),Gt=(Vt,Et) (1) domains(variablexvp)←Ri(Vp,Vt); //step1 (2) automorphism groupG←autoDetect(Gp); //step2 (3) symmetry break constraints←analyze(G); //step3 (4)selectvariablexvp∈Vp//step4 (5)selectvaluevt∈domain (xvp) (6)ifsatisSBC && satisNDC (7)ifsatisfy constrains in VF2then (8) removexvpfromVp; (9) removevtfrom domain (xvp); (10) update values of variables; (11)ifdomain (xvp)==?then (12) throw exception INCONSISTENT; (13)ifvariables ((xvp)==?)then (14) solutions.add(); (15) return solutions; 算法第(1)行函數Ri根據模式圖和目標圖節點的度為每個變量返回初始值域。第(2)行函數autoDetect用于檢測圖中自同構并返回自同構群G。第(3)行函數analyze分析自同構群G并返回對稱破壞約束。在求解過程中,按節點度的大小依次選取變量,結合CSP的基于回溯求解方法,若當前賦值滿足SBC約束,NDC約束以及VF2相關約束,則通過alldiff約束更新剩余待匹配變量的值域。若變量未完全實例化前引起空值域,說明當前搜索分支無法找到解,算法向上回溯重新賦值;若變量完全實例化,變量集合為空,且對應賦值滿足所有約束條件,說明找到一個解,并將其添加進解集中。 為驗證本文算法的效率和正確性,在PC,Windows 7,3.5 GHz,8 GB內存環境下,使用Java語言實現算法程序,將本文算法與VF2算法及ILF算法進行了比較。實驗使用AIDS(http://jenalib.leibniz-fli.de)和PDBSV2(http://www.rcsb.org)兩個數據集,其中AIDS為抗艾滋病毒數據集,包含大量稀疏無向圖,每個圖表示化合物的原子結構。目標圖數據集中包含10 000個圖,平均每個圖包含27.4條邊。模式圖按邊的數量分為Q4、Q8、Q12、Q16、Q20、Q24這6組,每組內包含1000個小圖。PDBSV2 數據集包含40種蛋白質,將模式圖按邊數量分為Q4、Q8、Q16、Q32、Q64、Q128這6組,每組內包含8個小圖。目標圖為包含4000個-12 000個節點的中等稀疏圖。實驗結果以求解速度作為主要評價標準,其中實驗圖表中平均時間,通過統計所有模式圖與目標圖的求解時間,求解平均值所得,其計算公式如下 (1) 其中,Timeall為求解分組內所有模式圖和目標圖的總時間,Numpattern為分組內模式圖的數量,平均時間體現了求解單個模式圖與所有目標圖的所有解的效率。 基于本文所述,VFSBC算法通過對稱破壞約束,避免對稱子樹的搜索,從而有效避免對稱解的求解,降低了問題求解規模。在AIDS數據集中,平均求解時間如圖2所示,其對應自同構檢測時間如圖3所示。由對比結果可知,在規模為Q4時,本數據集下VFSBC算法求解速度達到最快,為VF2算法的2.57倍,統計Q4-Q24這6組實驗組,其平均求解速度是VF2算法的1.83倍。圖的自同構數量越多,本文算法的優勢越大,而自同構的檢測時間僅占求解時間的極小比例。若圖中沒有自同構,如模式圖為Q24的規模時,由于鄰域約束的限制,在一定程度上減少了值域范圍,相較VF2及ILF算法,同樣具有一些優勢。 圖2 AIDS數據集中求解速度對比 圖3 自同構檢測耗時 在PDBSV2數據集中,算法求解平均時間見表1,其對應自同構檢測時間見表2。表中參數“解的數量”用于比較在同一問題實例下,本文算法與其它算法求得解的數量。如在Q4規模下,VFSBC求得10 848個解,VF2求得 13 696 個解,說明其中有2848個解是重復解,在求解時,是不需要被計算的。實驗結果顯示,VFSBC算法的表現同樣優于VF2及ILF算法。在規模為Q16時,本文算法的求解速度是VF2的1.55倍,統計Q4-Q128這6組實驗組,其平均求解速度是VF2算法的1.18倍,平均減少1015個重復解。當模式圖的規模處于Q32以下時,自同構檢測時間依然占比甚微,但是隨著模式圖的規模增加,自同構檢測的時間所占比例逐漸增大。因為自同構檢測是一個連續發散的過程,一方面其檢測時間受劃分內單元數量影響;另一方面,其復雜度隨搜索樹深度的增加呈指數級增長。如何解決圖規模增大帶來的自同構檢測負擔,是需要進一步解決的問題。 表1 PDBSV2數據集實驗結果 表2 自同構檢測時間 針對子圖同構約束求解中重復解問題,本文提出一種破壞重復解的子圖同構約束求解算法。該算法基于改進的自同構檢測方法,生成對稱破壞約束,構建子圖同構問題的新的CSP模型,并利用CSP算法進行求解。實驗結果表明,該算法與傳統算法相比,有效減少了重復解的求解,在小規模及中等規模圖匹配中具有良好的求解效率。下一步工作將研究一種自同構預測模型,針對預測結果進行自同構檢測分類處理,以緩解圖規模增大時,原自同構檢測方法耗時過大的問題。1.2 變量對稱
2 基于對稱性破壞的子圖同構約束求解算法(VFSBC)
2.1 自同構檢測
2.2 對稱破壞約束
2.3 子圖同構CSP模型
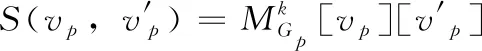
2.4 VFSBC算法偽代碼
3 實驗結果及分析
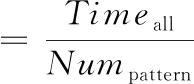


4 結束語

