改進灰狼算法及其應用

袁 巖，曹萃文

(華東理工大學 化工過程先進控制和優化技術教育部重點實驗室，上海 200237)

0 引 言

群體生物有各自獨特的群體規律性，學者們根據這些規律發掘出眾多群智能優化算法[1-3]。這些算法常被應用于復雜數學求解問題[4，5]和實際工程建模優化[6-8]問題，并取得了很好的效果。灰狼算法[9](grey wolf optimizer，GWO)作為新型的仿生智能優化算法之一，因其算法結構清晰、靈活，調節參數較少，尋優精度相對較高等優點被許多研究學者廣泛采用。為進一步提升灰狼算法的性能，文獻[10]提出了基于末尾探索者策略的改進灰狼算法，此算法提升了算法規避局部最優的能力；文獻[11]提出了基于貪婪思想和變異策略的改進灰狼算法，此算法提升了標準灰狼算法開發能力不足的問題。以上提出的兩種改進方式都在一定程度上解決標準灰狼算法的全局勘探開發能力，但是以上改進的兩種方式中位置更新策略和標準灰狼算法的位置更新策略大致相同，仍然存在容易陷入局部最優解的可能，算法的開發能力還有提升的空間。

針對以上問題，提出了一種改進的多策略灰狼算法(multi-strategy grey wolf optimizer，MSGWO)。MSGWO算法在標準GWO算法基礎上，在算法初始化階段加入對立搜索策略，在迭代計算過程中引入正弦余弦搜索策略和自適應局部搜索策略，加強算法全局探索開發能力、收斂速度和尋優精度。最后將MSGWO算法應用于8個測試函數的求解問題和加氫裂化數據建模參數的優化問題，對該算法的有效性和實際工程應用效果進行驗證。

1 灰狼算法

(1)包圍獵物

當狼群發現獵物時，灰狼會迅速向獵物前進，其灰狼的位置更新及灰狼與獵物的距離如式(1)-式(3)描述(設搜索空間為d維)

X(t)={Xi(t)|i=1,2,…,d}

(1)

(2)

X(t+1)=XP(t)-AD

(3)

其中，t表示當前迭代次數，X(t)表示第t代灰狼的位置向量，D表示灰狼與獵物間的距離向量，XP(t)表示第t代獵物的位置向量(用當前種群的當前最優解代入)，C和A為系數變量，分別由式(5)和式(6)計算得到

(4)

C=2r2

(5)

A=2ar1-a

(6)

其中，a在迭代過程中按式(4)線性從2降到0，max_it為最大迭代次數，r1和r2為[0,1]上均勻分布的隨機數。

(2)追捕獵物

當狼群包圍獵物以后，狩獵行為開始，根據適應度排序得到最優解Xα、次優解Xβ和當前第三優解Xδ。其中α、β、δ灰狼的位置更新如式(8)，剩下灰狼的位置更新受到α、β、δ灰狼的引導，其更新方式如式(9)所述

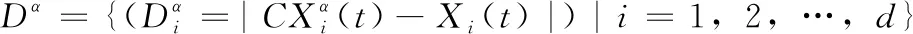
(7)

X1=Xα-ADαX2=Xβ-ADβX3=Xδ-ADδ

(8)

(9)

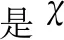
(3)攻擊獵物

如上所述，待獵物停止移動時，灰狼開始攻擊獵物。此過程可用數學描述為，A為[-a,a]之間的一個隨機值，當A的值在[-1,1]范圍之外時，搜索代理可以在灰狼當前位置和獵物位置之間的任意位置進行局部搜索，當A的值在[-1,1]范圍之內時，灰狼必須攻擊獵物。

2 改進的灰狼算法

2.1 對立搜索策略

GWO算法初始化種群位置采用的是隨機初始化的方式，隨機初始化種群個體位置有可能導致可行解的搜索范圍變大，搜索時間延長，搜索速度較慢等缺點，進而影響整個算法的收斂速度。

本文在隨機初始化的基礎上添加對立搜索策略，其基本思想是在隨機初始化的種群個體時，產生其對立個體，并將對立個體和此隨機初始化個體進行適應度評價對比，當對立個體適應度評價優于此個體時就采用此個體，否則使用隨機初始化的個體。數學表達式如下

(10)

其中，Ub、Lb為X的上下界，X(0)為初始化位置向量

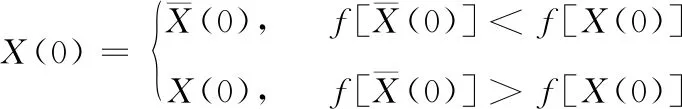
(11)

2.2 正弦余弦搜索策略

在GWO算法中，狼群的位置更新主要受到α、β、δ灰狼的引導，為提高GWO算法搜索精度，本文引入Seyedali Mirjalili的正余弦搜索算法[12]。即狼群在α、β、δ灰狼按式(9)的引導進行位置更新之后，再進行一次正弦余弦搜索。正弦余弦搜索的數學表達式如下

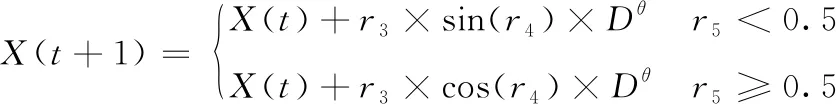
(12)

(13)

(14)

r4∈(0,360°)

(15)

式中：r3隨迭代次數的增加而自適應減少，a為常數此處取值為2。r5，r6為[0,1]上的均勻分布的隨機數。正余弦交叉搜索策略可以防止算法早熟從而提高算法的尋優精度。

2.3 自適應局部搜索策略

為提高GWO算法規避局部最優的能力，提出自適應局部搜索策略。GWO算法將α狼的位置作為算法的最優解，加入自適應局部搜索策略后，對最優位置Xα進行局部搜索，即在最優位置進行鄰域搜索。最后將得到的新的最優解的鄰域值與最優解逐個進行適應度比較，選取適應度好的個體作為新的最優解。

在迭代更新過程中，鄰域搜索范圍也會隨迭代次數逐漸縮小，平衡了搜索速度和尋優精度，達到自適應搜索的目的，其數學表達式如式(16)描述

Xα(t+1)=(1-ε)Xα(t)+εRand

(16)

式中：ε為自適應系數，其元素值由式(17)決定

(17)

其中，Rand為d維的向量,其向量元素值為[0,1]上的均勻分布的隨機數。

2.4 MSGWO算法流程

MSGWO算法的計算步驟如下：

(1)設置種群規模、最大迭代次數、待優化問題維度；

(2)初始化種群位置，對隨機初始化位置進行對立搜索計算，比較隨機初始值和對立值的適應度值，選取適應度好的種群個體作為初始化種群；

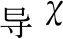
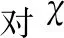
(5)對狼群個體進行適應度排序得到最優個體，對最優個體位置進行一次局部自適應搜索，并計算其適應度與最優值進行比較，選取適應度好的解作為新的最優個體；

(6)判斷運算結果是否滿足終止條件，滿足則算法結束，否則轉至步驟(2)。

3 實驗測試與分析

3.1 實驗測試

為檢驗改進后的灰狼算法性能，選取表1中的8個標準測試函數進行測試。仿真實驗采用的計算機配置詳細情況為：CPU為Intel Core i7-8550U，主頻為2.0 GHz，16 G RAM，操作系統為Microsoft Windows10 64位操作系統。計算環境為Matlab2017(b)。實驗測試中為檢驗改進算法對不同維度問題的處理能力，依次對表1中的8個測試函數分別進行20、30、50維測試。首先將MSGWO算法測試結果與GWO算法測試結果對比分析如圖1中的8個收斂曲線圖所示。然后將MSGWO算法和粒子群算法(particle swarm，optimization，PSO)、人工蜂群算法(artificial bee colony，ABC)、改進人工蜂群算法(improved artificial bee colony，I-ABC)對比分析，算法尋優求解結果使用求解平均值(Mean)和標準差(Std)作為對比指標在表2中展示，其中ABC、I-ABC算法中的數據源自文獻[13]。

表1 無約束測試函數

為客觀公正評價算法的性能，對算法選取以下的參數設置：4個算法種群規模均設置為40，最大40 000次適應度評價，分別獨立運行50次取平均值。運行結果見表2，黑體加粗數據表示MSGWO算法較GWO算法尋優結果更好。

3.2 實驗分析

(1)由表2可以看出，MSGWO算法相比較GWO算法對8個測試函數在20、30、50維尋得7次最優，尤其對f1、f2、f3、f6、f8測試函數尋優時，尋優精度提升明顯，說明改進后的算法是有效的。表2數據顯示，在測試函數高維(50維)尋優求解時，MSGWO算法同樣表現出色。

(2)標準差用于反映算法求解尋優的穩定性，由表2的標準差列數據對比可以看出，MSGWO算法對8個測試函數的標準差值7次小于GWO算法，說明MSGWO算法的穩定性較好。

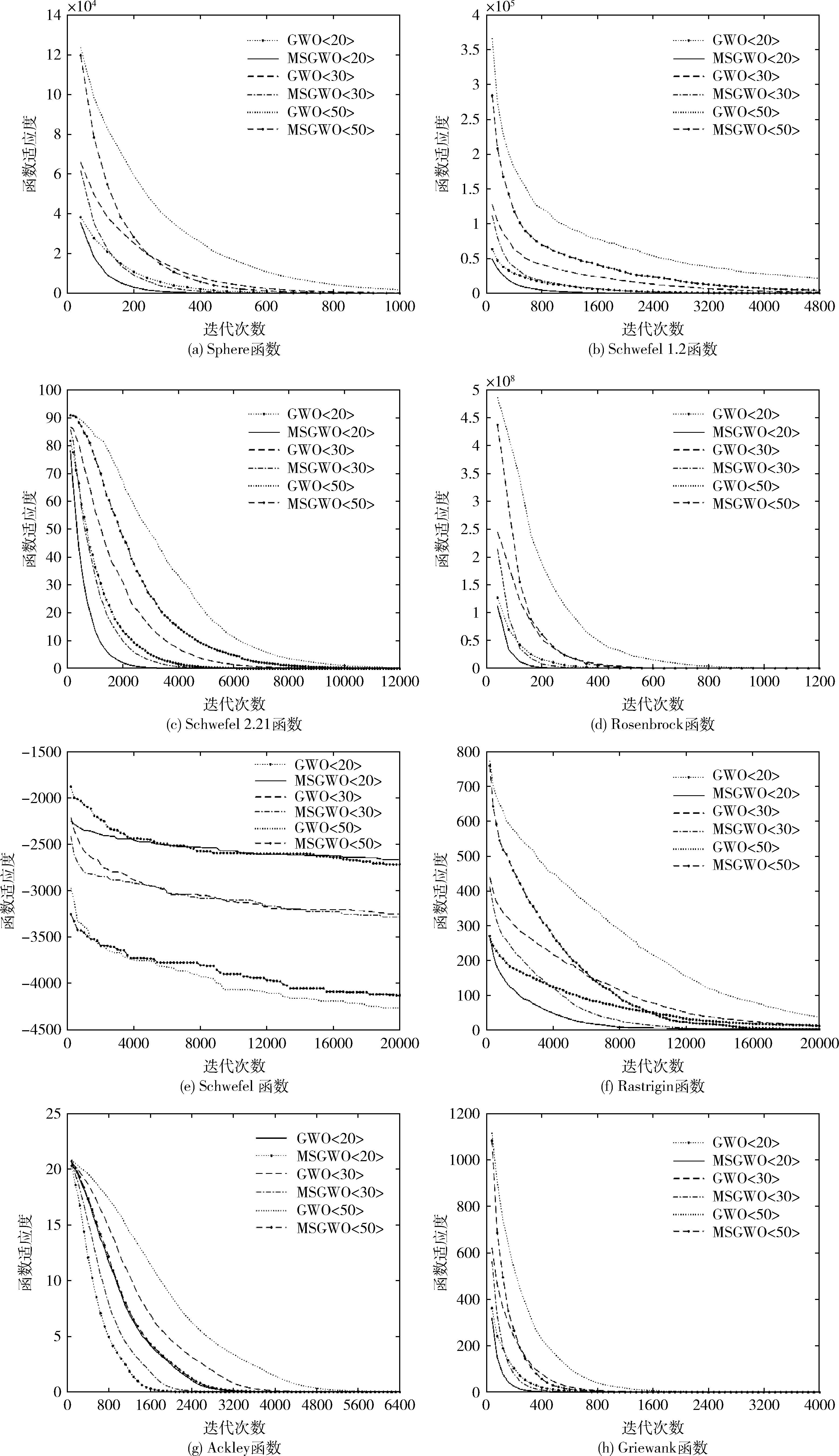
圖1 測試函數的收斂效果

(3)圖1中8個收斂曲線圖顯示，對于8個測試函數的20維、30維、50維等3個不同維度上的求解計算，MSGWO 算法收斂速度均快于GWO算法的收斂速度，表明MSGWO算法的收斂速度較快，改進效果很好。

(4)表2可以得到，MSGWO算法對Rastrigin、Griewank兩個測試函數取得全局最優值，對于測試函數Schwefel，GWO算法求解時易陷入局部最優，而MSGWO算法能夠跳出局部最優更接近理論最優值，說明改進灰狼算法采用局部自適應搜索策略能夠一定程度上規避局部最優解，從而提升算法的全局勘探開發能力。

4 算法實例研究

4.1 最小二乘支持向量機

支持向量機(support vector machine，SVM)是一種二分類算法模型，采用最大間隔的學習策略，是數據驅動建模技術中的一種重要方法。最小二支持向量機(least squares support vector machine，LSSVM)是SVM的改進，把SVM中的優化約束中的不等式約束轉化為等式約束問題，避免了求解二次規劃問題，降低了計算復雜性，使得易于實際應用和大規模的數據建模場景。LSSVM優化問題的數學描述為：

設有n個樣本組成的樣本訓練集

T={(xk,yk)|xk∈Rn,yk∈R,k=1,2,…,n}

(18)

其中，xk為輸出向量，yk為輸出變量。

可以構造一個分類函數

y(x)=wTφ(x)+b

(19)

其中，b為偏置變量，φ(·)∶Rn→Rnk為非線性映射函數，即將原輸入特征空間映射到一個高維特征空間，w∈Rnk為權重系數向量。

那么LSSVM的最優化目標問題可以表述為

表2 算法優化對比結果

表2(續)

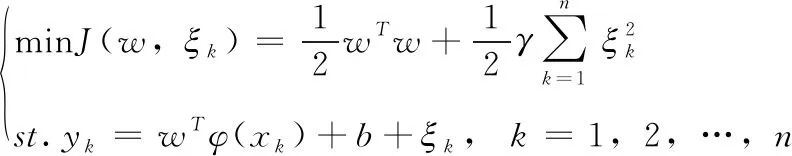
(20)

為解決該最優化問題構建拉格朗日函數為

L(w,b,,k))

(21)

對其求偏導數，得到

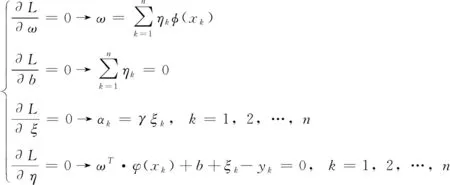
(22)

通過引入核函數

K(xk,xl)=φ(xk)·φ(xl),k,l=1,2,…,n

(23)

擴展到非線性領域，可獲得線性方程組

(24)

通過上式，可以求得LSSVM的模型

(25)

其中本文中選用的函數為高斯徑向基核函數

(26)

4.2 數據建模輸入輸出變量設計

單段串聯加氫裂化工藝原理：原料油與氫氣經加熱爐后進入加氫精制反應器、加氫裂化反應器進行加氫精致、加氫裂化反應。反應產物降溫后經熱高壓分離器后進入冷高壓分離器進行油、水、氣三相分離。冷高壓分離器底部的生成油經減壓后送入低壓分離器，其流出物進入汽提塔，塔底流出物經加熱后送入分餾塔，得到輕石腦油、重石腦油、航空煤油、柴油以及渣油[14,15]。

根據加氫裂化工藝原理以及使用Aspen Hysys模擬加氫裂化工藝流程靈敏度分析，得到影響加氫裂化產品產量以及產品性質的主要操作條件是[16]：原料油流量、反應氫油比、反應空速、反應壓力、新氫補充量、循環氫耗量、反應器1床層1溫度、反應器1床層2溫度、反應器2床層1溫度、反應器2床層2溫度，所以選取以上10個變量作為數據建模的輸入變量。選取航空煤油產量、航空煤油硫含量、航空煤油氮含量、航空煤油烷烴量、柴油產量、柴油硫含量、柴油氮含量、柴油烷烴含量共計8個輸出變量作為預測目標變量。

4.3 數據驅動建模及參數設計

實驗數據為某煉油廠實際采集的288組數據，隨機選取220組數據作為訓練數據集，剩余68組數據作為測試數據集。為說明改進算法的有效性，本文在Matlab2017(b)環境下，構建以下5種預測模型：①BP神經網絡預測模型；②RBF神經網絡預測模型；③PSO-LSSVM預測模型；④GWO-LSSVM預測模型；⑤MSGWO-LSSVM預測模型等共5個加氫裂化裝置產品預測模型。

建模過程中的參數設置為：BP神經網絡學習率為0.1，神經網絡訓練次數為1000；為保證所建模型使用算法對比的公平性，PSO、GWO、MSGWO等優化算法種群數統一設置為40，算法迭代次數均設置為500次。

預測目標誤差選擇：誤差評價指標選擇平均絕對誤差(mean absolute deviation，MAD)，相對平均百分誤差(mean absolute percentage error，MAPE)和均方根誤差(root mean square error，RMSE)，其計算方式分別如式(27)-式(29)所示

(27)

(28)

(29)

目標函數：待優化的LSSVM模型的參數為式(20)中懲罰因子γ， 以及式(26)中核參數σ， 參數區間設置為γ∈[0.01 500],σ∈[0.01 30]， 優化的目標函數為

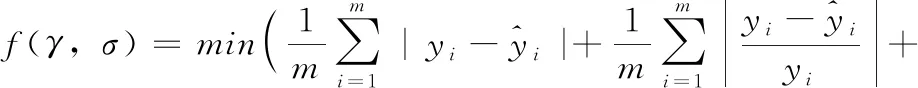
(30)

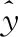
4.4 模型預測結果分析

PSO、GWO、MSGWO算法尋優γ和σ結果見表3。

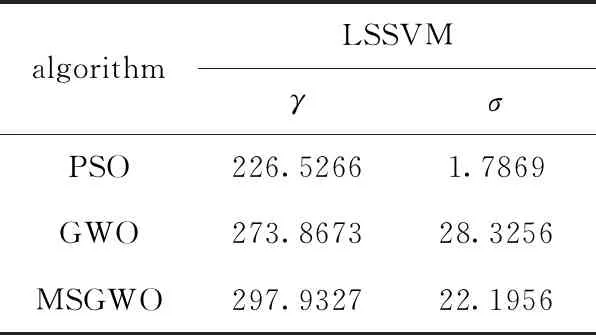
表3 算法尋優γ和σ結果

本文選用MAPE和RMSE作為預測效果檢驗指標，預測結果見表4，黑體表示4種模型中結果最優值。其中表4中以“D_”開頭表示柴油性質，以“J_”開頭表示航煤油性質。預測效果如圖2所示(為使圖形清晰直觀，程序中選取68組測試數據集中的前20組數據作圖分析對比)。

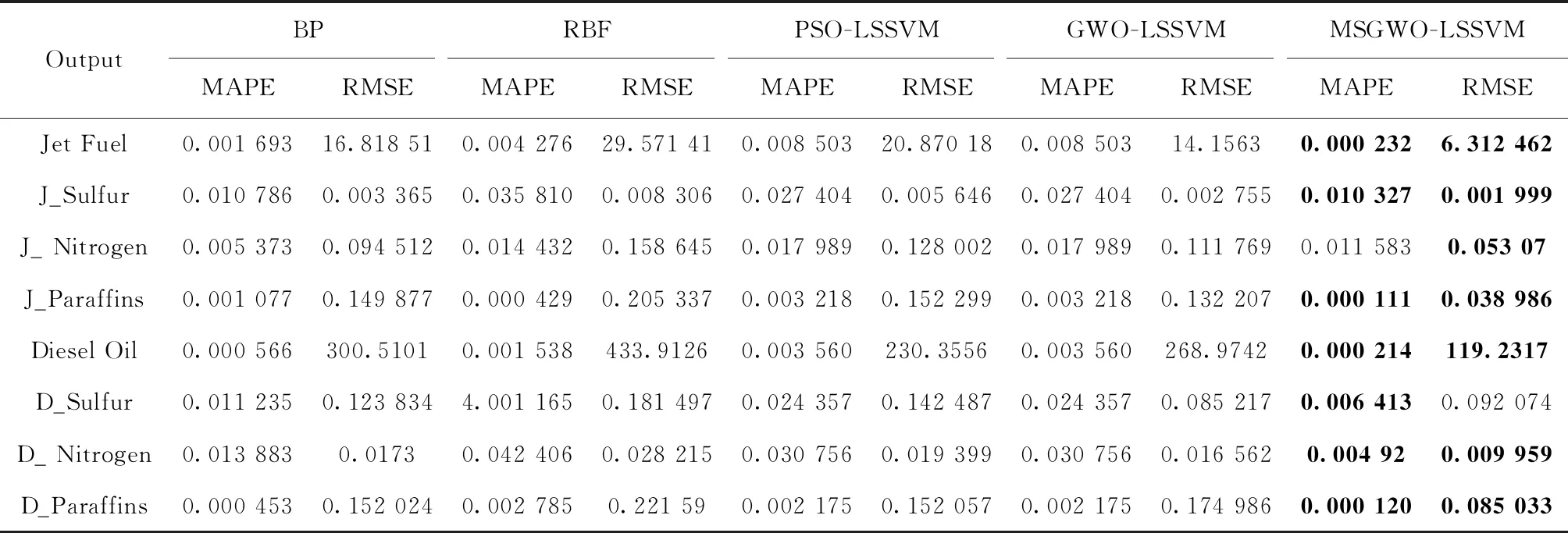
表4 5種預測模型預測對比結果

由表4和圖2可以看出，相比較其它4種預測模型，對于8個預測目標變量在MAPE和RMSE兩個指標上MSGWO-LSSVM模型的預測精度6次最好，在航煤油氮含量預測上MAPE指標不是最好但是和其它模型相比差距很小，

圖2 各模型預測值對比

RMSE指標相對其它預測模型是最小的。在柴油硫含量預測上RMSE指標不是最好的，但是MAPE指標是最小的。說明所建MSGWO-LSSVM模型的預測效果是比較好的，具有一定的預測價值。這也進一步說明MSGWO算法在解決實際工程應用上的有效性和可行性。

5 結束語

本文針對GWO算法開發能力不足、收斂速度慢、易陷入局部最優等問題，提出了MSGWO算法，主要進行以下3個方面的改進：加入對立搜索策略進行種群位置初始化；加入正弦余弦搜索策略，提高算法的尋優精度和開發探索能力；加入自適應局部搜索策略，以提高算法的全局搜索能力防止陷入局部最優。使用8個Benchmark函數對MSGWO算法進行實驗測試，并與GWO算法以及PSO、ABC、I-ABC算法進行比較，仿真實驗結果表明，MSGWO算法在求解精度和收斂速度以及尋優穩定性上表現較好。

最后將MSGWO算法用于加氫裂化數據建模參數優化問題，建立MSGWO-LSSVM加氫裂化產品預測模型，并和其它4種預測模型對比分析，仿真結果說明MSGWO-LSSVM模型的預測精度較高，可靠性好。此模型可以較準確地預測出在操作工況條件變化下加氫裂化裝置產品的產量以及產品性質，進一步驗證了算法的有效性。