基于PCA的哈希圖像檢索算法

馬紹覃，張 鴻

(1.武漢科技大學 計算機科學與技術學院，湖北 武漢 430065；2.武漢科技大學 智能信息處理與實時工業系統湖北省重點實驗室,湖北 武漢 430065)

0 引 言

基于哈希[1-6]的圖像檢索技術致力于解決大規模數據集下圖像的查找問題，通過將原圖像轉化為二進制編碼表示，圖像特征轉化為對應的二進制編碼，不僅可以極大壓縮存儲空間，還能夠大幅度提高檢索速度。

圖像哈希技術的主要步驟可分為投影與量化，已有學者證明[7]，兩個階段對于圖像哈希編碼的性能都有著巨大的影響。而現在的研究更加偏向于投影階段，對于量化階段研究較少。本文同時從兩個方面進行分析，在投影階段，將主成分分析(principal component analysis)嵌入，對原數據特征矩陣進行降維，將其投影到新的特征空間中，同時盡量降低了信息的損失。在量化階段，不同于現在大多數哈希算法所采用的單比特量化(single-bit quantization，SBQ)，使用了一種全新的量化方法，稱為適應性比特量化(adaptive-bit quantization，ABQ)，減少量化帶來的誤差。最后，通過綜合性的實驗驗證了所提算法的有效性。

1 相關工作

圖像哈希技術源自于20世紀90年代末，其思想是利用哈希函數將表示原圖像的高維特征映射到低維的漢明空間中，同時以一定的概率保證在原空間中距離較近的點投影后距離也近，而距離較遠的點投影后距離也遠，然后在低維的漢明空間中，利用漢明距離來衡量點之間的相似度。如果能產生良好的哈希編碼去表示原圖像，不僅能夠顯著地提升計算速度，因為比較距離只需要進行簡單的位運算，而且還可以大幅度降低存儲量，比如，原來空間中每個數據樣本都被一個1024 B的向量表示，一個包含一億個樣本的數據集需要占用100 GB的存儲空間。但是,如果把每個數據樣本都映射為128位的哈希碼表示，一億個樣本的存儲空間只需要1.6 GB。

圖像哈希算法基本上可分為兩大類，一類是數據獨立型的，較為經典的是局部敏感哈希(locality sensitive hashing，LSH)[8]和其擴展方法[9]等，這類方法不依賴于具體的數據，采用多個隨機生成的函數構成投影函數簇，然后量化得到最終的哈希編碼，隨著編碼位數的提高能獲得較好的編碼效果。一類是數據依賴型的哈希算法，也稱為基于學習的哈希算法[10-12]，通過分析樣本數據的信息來構造投影函數，如數據固有的結構信息和語義信息等。在兩類哈希算法中，通過學習得到的哈希函數相比較隨機映射的哈希函數，在編碼位數相同的情況下，前者比后者編碼的效果普遍更好，所以現在的研究熱點基本上都是針對于前者。在數據依賴型的方法中，基于PCA的哈希算法是較為經典的[13-15]，其大致做法是首先對原數據做PCA，得到降維矩陣后再進行量化處理。但是，對于PCA來說，方差越大的方向攜帶的信息也越多，將各個方向的投影數據等比特編碼會導致極大的量化誤差，現在的大多數方法都是采用的單比特量化，即將投影后的數據，每一位都與設定的閾值相比較，大于閾值量化為1，小于則量化為0。這樣不僅忽略了不同方差方向所攜帶信息的不同，也使得閾值兩邊極為接近的數據被量化成了不同的比特位。Weiss等[13]為了減少量化的損失，使用拉普拉斯特征函數公式在數據范圍大的方向分配更多的比特，但是這種方法依賴于數據在高維空間均勻分布的假設之上。Wang等[14]為了捕獲數據方差大的方向，對其目標函數進行了一系列的放松，雖然最后的實驗效果有所改善，但是沒有擺脫單比特量化的局限性。

2 研究方法

在本文中，為了保證最后哈希編碼性能的優越性，將從投影和量化兩個階段進行研究。投影階段，通過分析，嵌入PCA算法；量化階段，結合投影方法的特性，提出了適應性比特量化算法(ABQ)。具體來說，即將PCA投影后的數據，根據閾值劃分量化空間，對不同空間的數據采取不同的量化方法，減少誤差的同時，保證量化速度。

2.1 PCA嵌入

根據Weiss等[13]，Wang等[14]以及香農定理，要想得到緊湊且有效的哈希編碼，編碼后每個比特之間的方差應該最大且編碼之間要互不相關。所以最大化如下目標函數

(1)

W為投影矩陣，其維度與具體的量化函數有關，后面會做具體的分析，x={x1,x2,…,xn} 為數據集，xi∈Rd， var(·) 表示一個向量或矩陣的方差，h(x) 表示數據集x對應的哈希函數，q(v) 表示量化函數，hk(x)=q(xtk)，B是量化后編碼矩陣，B∈Rn×c。 由于式(1)的離散問題和編碼之間正交的限制，我們將目標函數進行放松

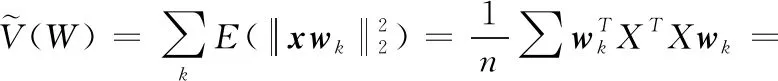
(2)

X∈Rn×d是由xi組成的數據矩陣，式(2)所尋求的目標和PCA正好是一致的，尋找協方差矩陣XTX的前k個最大的特征值對應的特征向量所組成的投影矩陣W， 用于最大限度保留原始數據的整體相似性。W的維度或者說k的大小與具體量化方法有關，后面會做相關的分析。

2.2 適應性比特量化

針對單比特量化和雙比特量化(double-bit quantization，DBQ)在基于PCA哈希量化過程中的優勢與缺陷，我們提出了ABQ。按照PCA的理論之一，其投影矩陣W是逐一選取方差最大的方向所組成的，方差大的方向上的投影所包含的信息量會更大，也就是說，這一部分的信息會更加重要，應該在量化的過程中體現這一重要特性，僅僅使用SBQ或者DBQ這樣等比特編碼方式是無法做到的。上一小節提到過W的維度或者說特征向量k的個數是與量化函數和編碼長度有關的。設編碼長度為c，若采用SBQ，則k的大小等于c，因為投影后每個數據位量化為一個比特位，這樣SBQ最大程度的利用了投影矩陣，保留了更多的編碼信息，但缺點是量化誤差較大。采用DBQ則k等于c的一半，相比SBQ，DBQ只利用到投影矩陣的一半，加快了速度，但是同時也丟失了更多的編碼信息。本文提出的ABQ不僅速度上要快于SBQ，而且相比DBQ保留了更多的編碼信息。對于長度為c的編碼，首先確定一個比例系數λ，依據λ去劃分待量化的數據域，對于原特征空間中投影后的新特征空間中的向量，認為數據位的前λc位是比較重要的，每位量化為兩個比特，而數據位的后c-λc位相對來說次要一些，每位量化為一個比特。

3 算法實現

本文算法大致分為兩步，投影與量化。投影階段運用PCA，將數據矩陣X∈Rn×d映射到新的低維空間(這里假設數據矩陣是零中心化的)，得到降維矩陣Z∈Rn×k。 對于新的特征空間采用ABQ進行量化。

投影階段之前已做了較為詳細的分析，不再重述，在量化階段，首先確定一個比例系數λ， 實驗結果表明設置λ=0.75在不同位數的編碼上都能取得較好的效果，我們也會給出λ 取不同值情況下的實驗對比效果。對于待量化的數據，單比特量化的部分，使用如下方法

(3)

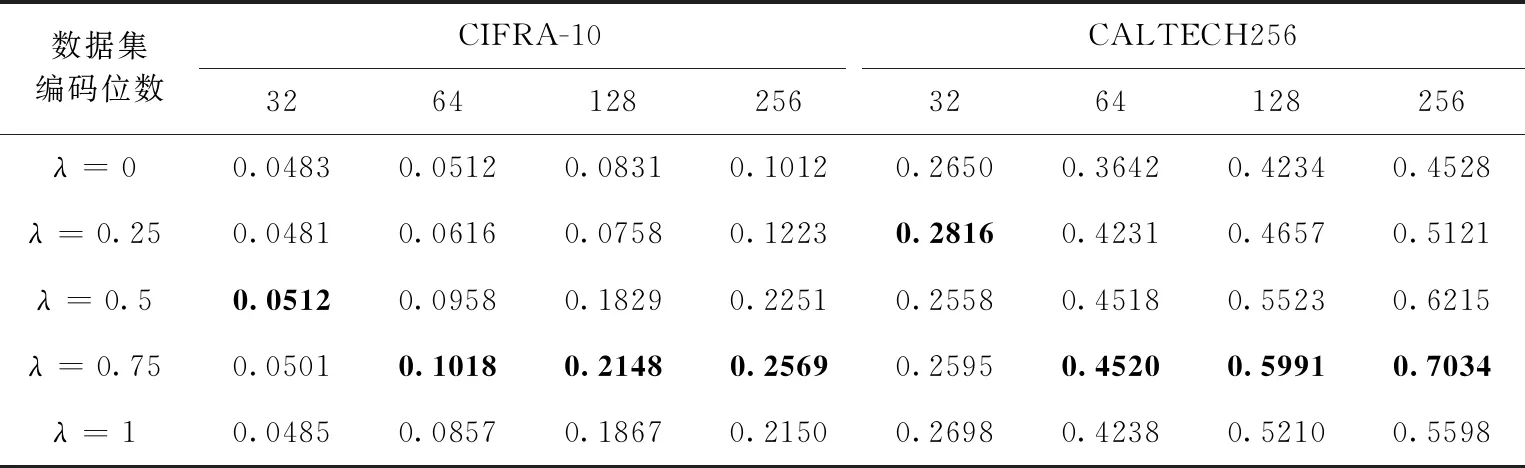
對于雙比特量化的數據，我們采用一種動態閾值劃分的方法，根據待量化的數據獲取一個下閾值a和上閾值b， 通過a和b將需要量化的數據劃分為3個子集S1={x|-∞

(4)

μi表示子集Si的均值。首先設置μ2為0，表示中間子集S2以0作為均值，那么式(4)轉化為

(5)

|Si| 表示相應子集Si中元素的個數。可以看出，式(5)的第一部分為常量，則最終優化目標轉化為最大化如下目標函數

(6)

通過式(6)學習到動態閾值a和b， 將待量化的數據劃分為3個區域。采用如圖1(b)的方法進行量化。結合單比特量化階段數據編碼的結果，組合成最終的編碼矩陣B=[b1,b2,…,bc]。 DBQ算法流程如下所示：

算法1：DBQ算法流程

輸入：數據集S；

輸出：閾值上限a， 閾值下限b；

(1)將數據劃分為3個子集：

S1={x|-∞

S2=?，

S3={x|0

(2)將S1和S3分別排序，設置max=0；

(3)判斷S1或者S3是否為空集，如果為空轉向步驟(4)，否則轉向步驟(8)；

(4)計算S2中的數據和，如果小于等于0，則把S3中最小的數移到S2中，反之則把S1中最大的數移到S2；

(5)根據式(6)計算F；

(6)比較F與max的大小，如果F大于max, 則把max更新為F， 設置a為當前S2中的最小值，b為當前S2中的最大值；

(7)回到步驟(3)；

(8)返回a和b。

圖1 (a)SBQ與(b)DBQ的量化效果

算法的全部流程如下所示：

算法2：PCA-ABQ算法流程

4．地勢高危，道路險要。因王罕嶺山體三面騰空而起，而剩下的一面又是連接大湖山主峰，山勢坡度大，懸崖峭壁分布眾多，從而形成了古詩文所述的“高崖萬沓，邃澗千回”“喬峰迥峭，擘漢分星”“其險如崩，其聳如騰”和“白云生石壁”等自然特征。如人要上王罕嶺，必須沿騰空的山巖攀登，路途之艱險就不難想象了。

輸入：訓練集X∈Rn×d， 比例系數λ， 編碼位數c； 輸出：矩陣B∈Rn×c。

(1)通過式(2)計算出投影矩陣W；

(2)根據步驟(1)的結果將原數據進行投影得到低維空間的數據，Z∈Rn×k；

(3)將Z按照λ， 劃分為兩個子矩陣，Z1和Z2， 對于Z1采用雙比特量化得到編碼矩陣B1， 對于Z2采用單比特量化得到編碼矩陣B2；

(4)組合B1和B2得到最終編碼矩陣B。

4 實驗結果和分析

4.1 數據集

CIFAR-10：CIFAR-10數據集包括60 000張彩色的圖片，被劃分為10個圖像類別，每張圖片包含32×32個像素點，實驗中以512維的GIST描述子表示。

CALTECH256：CALTECH256數據集包含256種類別的物體，大約30 607張圖像，每類包含圖片最少80張，最多827張。每張圖片用一個2048維的特征向量表示。

4.2 實驗對比方法

LSH(locality sensitive hashing)：數據獨立型的哈希算法，其哈希函數為隨機生成的線性函數。

SH(spectral hashing)：將圖像特征向量的編碼過程視為圖分割問題，借助于對相似圖的拉普拉斯矩陣特征值和特征向量的分析對圖的分割問題提供一個松弛解。

KLSH(kernelized locality sensitive hashing)：核局部敏感哈希，將目標函數映射到核空間。

DSH(deep supervised hashing)[16]：針對單純地使用隨機投影帶來的較大誤差，通過分析數據的幾何結構，選擇與原始數據分布最相似的哈希函數。

SPH(spherical Hashing)[17]：使用基于超球面的哈希函數將數據點映射成二進制向量。

4.3 評價指標

MAP(mean average precision)：檢索得到的所有訓練樣本的平均準確率，被廣泛地應用在哈希算法性能的評判中。

Precision-Recall：Precision即查準率，Recall為查全率，前者是指檢出的相關目標數占檢出總數的百分比，反映了檢索的準確性；后者指檢索的相關目標數占系統中相關目標總數的百分比，反映檢索的全面性。通常是希望檢索結果的查準率越高越好，同時查全率也越高越好，但實際上這兩個指標是負相關的關系。在信息檢索中常常使用Precision-Recall曲線來評判檢索性能，其曲線高低和檢索效果是呈現正相關關系的。

4.4 性能分析

實驗分別在兩個數據集上進行，每個數據集隨機取1000個樣本作為測試數據集，剩余的樣本作為訓練數據集。為了保證實驗效果的公平和準確，我們在每種方法上循環10次以獲取最終的實驗結果。并以圖表的形式展現。表1展現的是λ 設置不同值時，在CIFAR-10數據集和CALTECH256數據集上MAP值。值得說明的是λ=0時對應為SBQ，λ=1時對應DBQ。從實驗的結果可以看到λ=0.75時，在兩個數據集上的檢索效果基本上都是最好的，如在CALTECH256數據集上，相比SBQ其MAP值平均提高了12%，比DBQ提高了6%，這是因為此時不但很好地減少了量化誤差，也盡可能多地保留了投影信息，這也可以說明量化階段對于編碼性能的重要性。其中CALTECH256上的MAP值在整體上要高于CIFRA-10，是因為樣本特征提取方法不同的緣故，本文研究的重點不在于此，故不做贅述，但這并不影響對實驗效果的分析與比較。圖2和圖3對應了不同哈希算法兩個數據集上的PR曲線,我們提出的PCA-ABQ在不同位數上的編碼效果均要優于現有流行的哈希算法。可以看到，PCA-SBQ方法在整體上的編碼效果是比較差的，因為量化所帶來的誤差太大，雖然保留了較多的投影信息，但是量化的誤差也較大，PCA-DBQ的檢索效果整體上則要優于PCA-SBQ，因為減小了量化帶來的誤差，而PCA-ABQ充分利用了基于PCA哈希的特性，在減少量化誤差，與保留投影信息之間尋找到一個平衡點，取得了最好的檢索效果。相較于隨機投影的哈希算法，PCA-ABQ無論是在低位和高位編碼上都能取得較好的檢索效果，而基于隨機投影的算法，在低位編碼上的性能是比較差的，因為其哈希函數的碰撞幾率比較大，只有在編碼位數比較高的情況下，才能達到較好的檢索效果。

表1 λ取值不同時在兩個數據集上的MAP值

圖2 不同哈希算法在CIFAR-10數據集上的precision-recall曲線

圖3 不同哈希算法在Caltech256數據集上的precision-recall曲線

5 結束語

本文基于PCA哈希的相關理論，提出了一種高效的哈希算法——PCA-ABQ。對于圖像哈希的兩個階段，投影與量化，投影階段我們采用現在流行的降維方法PCA將原特征空間的數據映射到新的子空間。量化階段，針對PCA的特性，采用一種分段量化的思想，通過實驗來確定最佳的比例系數。實驗中，我們在不同數據集，不同評價指標上與現在主流的圖像哈希算法進行了對比，驗證了我們算法的優越性。但是仍然有值得改進的地方，在投影階段，是基于PCA構造的投影函數，使得訓練的時間比較長，量化階段是建立在PCA降維的基礎之上的，有一定的局限性。在今后的工作中，我們將進一步研究如何降低投影階段的時間復雜度，如何把這種分段量化的思想應用到其它的哈希算法之中。