二階隨機(jī)占優(yōu)約束下考慮訂購(gòu)能力的多產(chǎn)品報(bào)童問(wèn)題

付永彬, 孫海琳

(南京師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，南京 210023)

1 引言

經(jīng)典報(bào)童問(wèn)題即單周期庫(kù)存問(wèn)題(Single-Period Problem, SPP)，其研究對(duì)象為生命周期短、易腐蝕、訂貨機(jī)會(huì)只有一次的產(chǎn)品，主要研究其訂貨問(wèn)題和庫(kù)存決策問(wèn)題，是供應(yīng)鏈管理中最重要的模型之一．隨著生產(chǎn)和銷(xiāo)售的復(fù)雜化，學(xué)者們將經(jīng)典的報(bào)童模型擴(kuò)展為多產(chǎn)品報(bào)童模型(Multi-Product Newsvendor Problem, MPNP)，通過(guò)在各種產(chǎn)品之間合理分配有限的資源，使報(bào)童總的期望利潤(rùn)最大或損失最小．

Whitin[1]首次建立了受價(jià)格影響的報(bào)童模型；Khouja[2]對(duì)報(bào)童問(wèn)題的擴(kuò)展模型做了分類(lèi)說(shuō)明；Mitra[3]以單產(chǎn)品報(bào)童問(wèn)題為背景，將產(chǎn)品的殘值、清倉(cāng)價(jià)格均視為決策變量，分別就季節(jié)性需求和季末需求是否外生和隨機(jī)建立了三個(gè)模型．Kyparisis 和Koulamas[4]分析了非負(fù)線性可加需求對(duì)單產(chǎn)品報(bào)童問(wèn)題訂價(jià)敏感度的影響．Wu 等[5]研究了單產(chǎn)品的報(bào)童博弈問(wèn)題，提出了兩種數(shù)量競(jìng)爭(zhēng)的需求分割規(guī)則，包括需求分配比例規(guī)則和需求再分配規(guī)則．Wang 等[6]考慮單產(chǎn)品報(bào)童模型，分別對(duì)風(fēng)險(xiǎn)中性和風(fēng)險(xiǎn)厭惡下隨機(jī)供應(yīng)對(duì)最優(yōu)訂貨量的影響進(jìn)行了研究．Mohammad 和Shokri[7]考慮風(fēng)險(xiǎn)厭惡條件下，以CVaR 為風(fēng)險(xiǎn)度量的多產(chǎn)品選擇問(wèn)題．Farahat 和Leeb[8]考慮在一般選擇規(guī)范下，即包含替代、互補(bǔ)、多單位訂購(gòu)、缺貨、庫(kù)存等情形，建立了客戶的對(duì)產(chǎn)品選擇模型．Shi 等[9]討論了供應(yīng)商數(shù)量折扣合同下，多產(chǎn)品多約束的聯(lián)合訂價(jià)及最優(yōu)訂購(gòu)量問(wèn)題；Murray 等[10]主要研究在資源能力有限條件下，報(bào)童的多產(chǎn)品訂價(jià)問(wèn)題；周繼祥[11]分別討論了訂貨無(wú)約束下、供應(yīng)商隨機(jī)生產(chǎn)約束下、資金約束下報(bào)童模型的顯式解；陳杰等[12]對(duì)具有多元馬氏需求特征的多產(chǎn)品庫(kù)存報(bào)童模型的優(yōu)化問(wèn)題進(jìn)行了探討；Ma 等[13]針對(duì)需求可替代的多產(chǎn)品報(bào)童問(wèn)題研究了其最優(yōu)產(chǎn)品組合及最優(yōu)訂貨量的聯(lián)合決策問(wèn)題．

在現(xiàn)實(shí)中大多數(shù)零售商是風(fēng)險(xiǎn)厭惡的，針對(duì)需求的不確定性所帶來(lái)的風(fēng)險(xiǎn)，許多學(xué)者采用不同的模型進(jìn)行研究．張艷霞等[14]對(duì)定常風(fēng)險(xiǎn)下具有不同風(fēng)險(xiǎn)偏好組合決策者的報(bào)童問(wèn)題進(jìn)行了風(fēng)險(xiǎn)分析；簡(jiǎn)惠云和許民利[15]針對(duì)風(fēng)險(xiǎn)規(guī)避和風(fēng)險(xiǎn)偏愛(ài)兩種情況，分別建立不同訂購(gòu)量和風(fēng)險(xiǎn)水平下的條件風(fēng)險(xiǎn)值模型，考慮缺貨成本，在一定條件下，得到任意風(fēng)險(xiǎn)水平下的VaR 解析表達(dá)式；周艷菊等[16]運(yùn)用前景理論，針對(duì)需求不確定條件下的兩產(chǎn)品訂貨問(wèn)題進(jìn)行了分析；Zhang 等[17]分別采用VaR 和CVaR 對(duì)單周期和多周期報(bào)童問(wèn)題進(jìn)行建模．

隨機(jī)占優(yōu)(Stochastic Dominance, SD)是風(fēng)險(xiǎn)管理的一種理論方法，已經(jīng)廣泛用于經(jīng)濟(jì)、管理學(xué)和金融學(xué)領(lǐng)域．Hadar 和Russel[18]首次提出隨機(jī)占優(yōu)的理念；Fishburn[19]整理出隨機(jī)占優(yōu)理論，并將隨機(jī)占優(yōu)理論應(yīng)用于組合投資問(wèn)題．作為一種重要的隨機(jī)占優(yōu)方法，SSD 可用來(lái)描述風(fēng)險(xiǎn)規(guī)避型投資者的行為．Dentcheva 和Ruszczyski[20]首次提出帶有SSD 約束的隨機(jī)優(yōu)化模型，他們通過(guò)引入新的變量把該問(wèn)題重新構(gòu)造成一個(gè)線性約束優(yōu)化問(wèn)題；Dentcheva 和Ruszczyski[21]分析了該問(wèn)題的最優(yōu)性與對(duì)偶性等問(wèn)題；Homem-De-Mello 和Mehrotra[22]結(jié)合了割曲面算法與樣本均值逼近(SAA)方法來(lái)求解帶SSD 約束的隨機(jī)優(yōu)化問(wèn)題；Sun 等[23]用光滑的罰函數(shù)SAA 方法來(lái)求解該問(wèn)題；Rudolf 和Ruszczyski[24]，F(xiàn)bin 等[25]分別采用切平面算法來(lái)求解帶SSD 約束的隨機(jī)優(yōu)化問(wèn)題；Sun 等[26]進(jìn)一步將切平面法改進(jìn)，更適宜解決大量非線性約束的凸優(yōu)化問(wèn)題；Yang 等[27]將SSD 應(yīng)用于供應(yīng)鏈系統(tǒng)，研究了多制造商多零售商之間最大化利潤(rùn)的交叉訂購(gòu)與定價(jià)問(wèn)題；羅曉琴等[28]將二階隨機(jī)占優(yōu)理論應(yīng)用于保險(xiǎn)資金資產(chǎn)組合優(yōu)化；吳敏等[29]考慮偏度因素，建立了SSD 約束下最大化組合收益率偏度的投資組合優(yōu)化模型；張宏偉等[30]采用SSD 理論對(duì)投資組合問(wèn)題進(jìn)行建模，并通過(guò)遺傳算法求解；楊柳和申飛飛[31]通過(guò)引入交易費(fèi)用函數(shù)，建立帶有SSD 約束的投資組合風(fēng)險(xiǎn)控制模型．

在隨機(jī)規(guī)劃問(wèn)題中，隨機(jī)變量未知．SAA 是一種經(jīng)典的、實(shí)用的估計(jì)隨機(jī)變量分布的方法．該方法利用隨機(jī)變量的經(jīng)驗(yàn)分布去近似其真實(shí)分布，有著深厚的理論基礎(chǔ)、良好的可操作性和應(yīng)用價(jià)值，在學(xué)術(shù)界已被廣泛論證和使用[32]．進(jìn)一步，SAA 在報(bào)童問(wèn)題中也是常用的方法[17]，部分原因是報(bào)童問(wèn)題的零售商可以比較方便地根據(jù)以往銷(xiāo)售情況獲得產(chǎn)品需求的各項(xiàng)信息作為SAA 問(wèn)題的樣本．這樣的樣本具有真實(shí)、利用率高等優(yōu)勢(shì)．

多產(chǎn)品報(bào)童問(wèn)題涉及庫(kù)存管理、風(fēng)險(xiǎn)管理、供應(yīng)鏈協(xié)調(diào)等多個(gè)領(lǐng)域．隨著風(fēng)險(xiǎn)控制領(lǐng)域的不斷發(fā)展，將新的風(fēng)險(xiǎn)測(cè)度應(yīng)用于報(bào)童模型既能體現(xiàn)新的風(fēng)險(xiǎn)測(cè)度的優(yōu)越性，又能對(duì)經(jīng)典模型帶來(lái)新的思路和啟發(fā)．本文建立了帶有隨機(jī)二階占優(yōu)約束的多產(chǎn)品報(bào)童模型，主要貢獻(xiàn)如下：

1) 本文首次將SSD 與報(bào)童問(wèn)題相結(jié)合，建立了帶有SSD 約束的多產(chǎn)品報(bào)童模型，考慮了在SSD 約束及訂購(gòu)能力約束下零售商的最優(yōu)訂購(gòu)策略；

2) 本文采用SAA 方法對(duì)帶有SSD 約束的多產(chǎn)品報(bào)童模型進(jìn)行逼近，并對(duì)SAA 逼近問(wèn)題進(jìn)行收斂性分析；繼而采用切平面法[26]對(duì)SAA 問(wèn)題進(jìn)行求解．?dāng)?shù)值實(shí)驗(yàn)的結(jié)果既驗(yàn)證了SAA 問(wèn)題的收斂性，同時(shí)又說(shuō)明了SSD 模型的優(yōu)越性．

2 SSD約束下的報(bào)童模型

2.1 模型介紹及參數(shù)設(shè)定

鑒于零售商總是同時(shí)訂購(gòu)和銷(xiāo)售多種產(chǎn)品，本文考慮對(duì)零售商在單周期內(nèi)對(duì)多種產(chǎn)品銷(xiāo)售的報(bào)童問(wèn)題進(jìn)行建模．現(xiàn)實(shí)中零售商往往不會(huì)把所有資金都應(yīng)用于產(chǎn)品訂購(gòu)，或者出現(xiàn)零售商訂購(gòu)能力有限，或資本難以周轉(zhuǎn)等其他情形，所以本文設(shè)定訂購(gòu)能力約束；同時(shí)又借助SSD 來(lái)規(guī)避風(fēng)險(xiǎn)．假設(shè)各種產(chǎn)品之間互不相關(guān)，不考慮訂貨提前期且貨源充足．產(chǎn)品的零售價(jià)格由市場(chǎng)決定，為已知量；訂購(gòu)價(jià)格和殘值由供應(yīng)商決定，為已知量；產(chǎn)品市場(chǎng)需求為隨機(jī)變量．零售商需要在銷(xiāo)售季到來(lái)之初，確定各種產(chǎn)品的訂購(gòu)量，以期獲得最大利潤(rùn)．

設(shè)共有M 種產(chǎn)品，對(duì)第m(m=1,2,··· ,M)種產(chǎn)品：訂購(gòu)量為xm, xm∈R+；市場(chǎng)需求為Dm, Dm: ? → Ξm是定義在概率空間(?,F,P)上的隨機(jī)變量，分別為單位銷(xiāo)售價(jià)格、單位訂購(gòu)價(jià)格、單位殘值，且pm>cm>vm>0．令

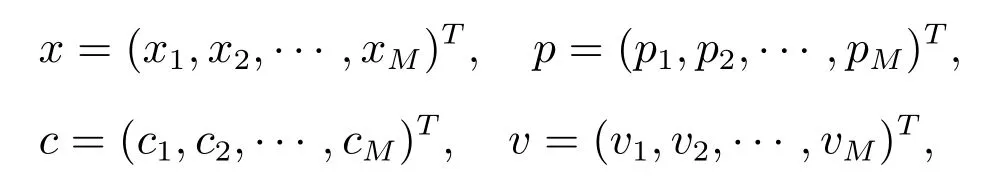
則在當(dāng)期對(duì)于第m 種產(chǎn)品，零售商的銷(xiāo)售量為min(xm,Dm)；庫(kù)存量為xm?min(xm,Dm)；銷(xiāo)售收入為pmmin(xm,Dm)；未賣(mài)出產(chǎn)品的殘值為vm[xm?min(xm,Dm)]；訂購(gòu)成本為cmxm．所以第m 種產(chǎn)品的利潤(rùn)為

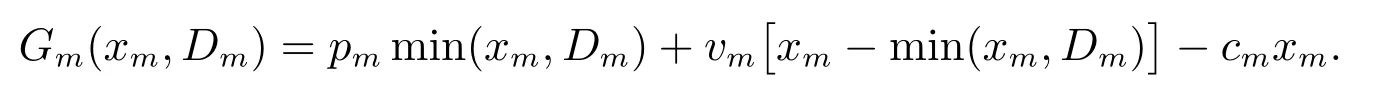
M 種產(chǎn)品的總利潤(rùn)為

由于min(a,b)=a ?(a ?b)+，其中(a ?b)+=max(a ? b,0)，上式可化簡(jiǎn)為

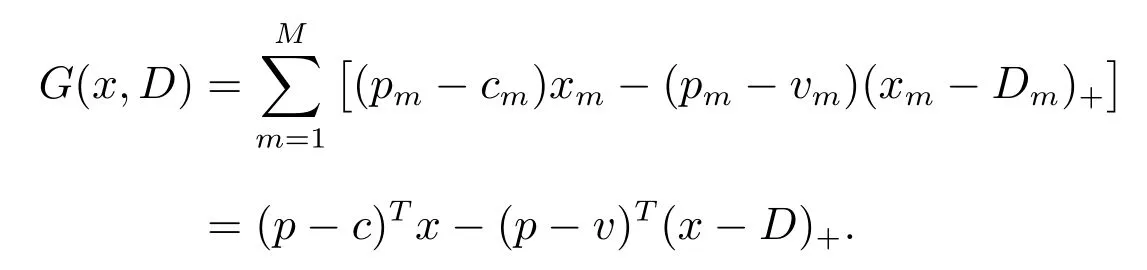
設(shè)J(x,D)=?G(x,D)表示損失函數(shù)．在訂購(gòu)能力約束下最小化期望損失的報(bào)童模型為

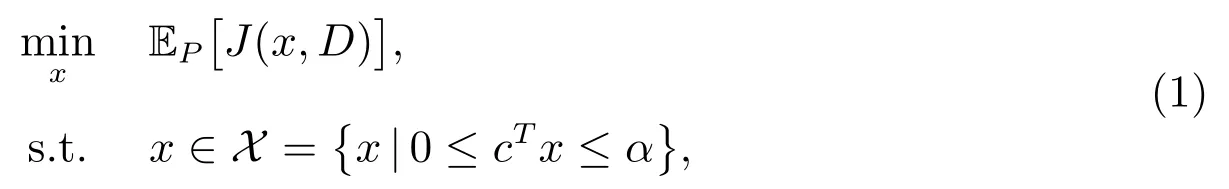
其中α 為常數(shù)，該模型也稱作風(fēng)險(xiǎn)中性模型．

2.2 SSD約束下的報(bào)童模型

在現(xiàn)實(shí)中大部分投資者是風(fēng)險(xiǎn)厭惡的，而問(wèn)題(1)未考慮風(fēng)險(xiǎn)因素對(duì)報(bào)童的影響．如前文所述SSD 可用來(lái)描述風(fēng)險(xiǎn)規(guī)避型投資者的行為，因此，本節(jié)引入SSD 約束，構(gòu)建帶有SSD 約束的風(fēng)險(xiǎn)規(guī)避型報(bào)童模型．

首先介紹SSD 的定義：設(shè)X(ω), Y(ω)分別為隨機(jī)變量ω 的兩個(gè)函數(shù)，其累積分布函數(shù)分別為FX(ω)(η)和FY(ω)(η)，即FX(ω)(η)=P(X(ω)≤ η)．令若滿足

則稱X(ω)一階隨機(jī)占優(yōu)于Y(ω)，記作X(ω)?1Y(ω)．令

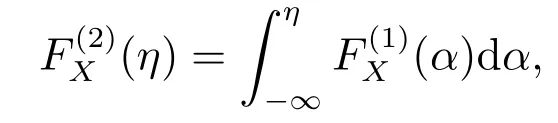
若滿足

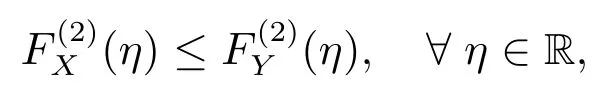
式(2)中Y(D)為基準(zhǔn)隨機(jī)變量．由SSD 性質(zhì)(文獻(xiàn)[20]中的2.6,2.7 式)，可知問(wèn)題(2)等價(jià)于

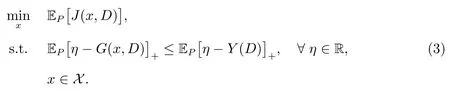
由于問(wèn)題(3)不滿足Slater 約束規(guī)范，所以考慮其松弛問(wèn)題

稱問(wèn)題(4)為真問(wèn)題，這里[a,b]是R 中一個(gè)有界閉區(qū)間．

3 SAA方法及其收斂性分析

本節(jié)研究真問(wèn)題(4)的SAA 問(wèn)題．設(shè)隨機(jī)變量D 的獨(dú)立同分布樣本為為方便起見(jiàn)，令Yi=Y(di)，則其SAA 問(wèn)題為

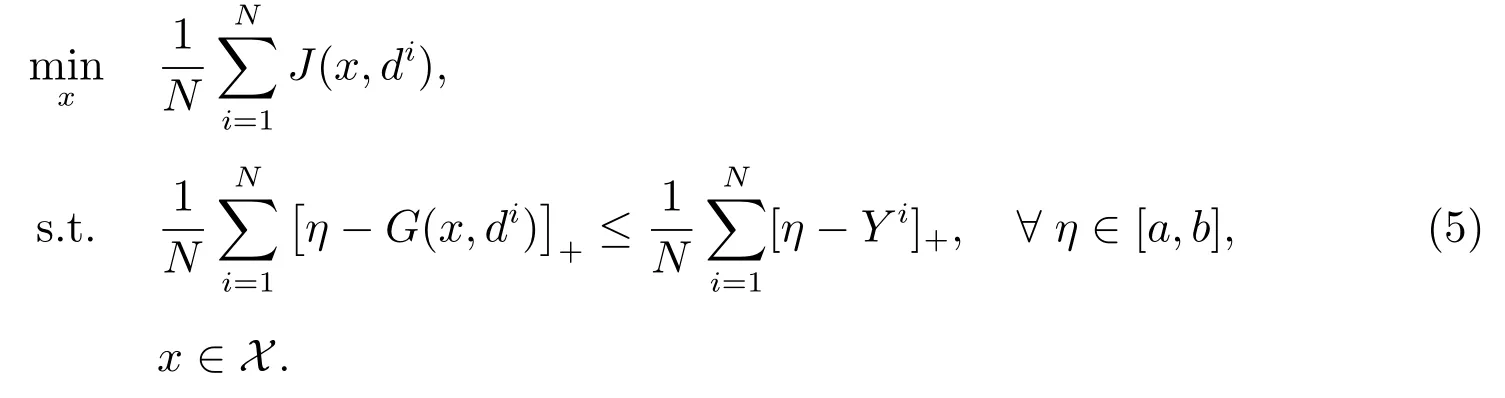
接下來(lái)給出SAA 問(wèn)題(5)的收斂性分析．

3.1 幾乎處處收斂

帶有SSD 約束的優(yōu)化問(wèn)題的最優(yōu)性條件已被Dentcheva 和Ruszczyski[20,21,33]證明．關(guān)于該問(wèn)題的SAA 問(wèn)題的收斂性在文獻(xiàn)[23,26,34]中也給了出來(lái)．這里根據(jù)報(bào)童問(wèn)題的特點(diǎn)，利用前述文獻(xiàn)的結(jié)果，證明了帶有SSD 約束的多產(chǎn)品報(bào)童問(wèn)題的SAA 問(wèn)題的收斂性．

為簡(jiǎn)化符號(hào)，令p(a)=max(0,a)，則有

命題1假設(shè)存在點(diǎn)x0∈X, η0∈[a,b]，使得

那么，我們有：

(i) 對(duì)任意的x ∈ X, η ∈ [a,b]，f(x)和h(x,η)是有定義的；J(x,D), G(x,D)關(guān)于 x 全局 Lipschitz 連續(xù)，Lipschitz 系數(shù)為

(ii) f(x)和h(x,η)關(guān)于x 是全局Lipschitz 連續(xù)的，Lipschitz 系數(shù)為k；且h(x,η)關(guān)于η 也是全局Lipschitz 連續(xù)的．

證明 對(duì)于結(jié)論(i)，由G(x,D)的顯式表達(dá)式可知，對(duì)xm, m=1,2,··· ,M，有

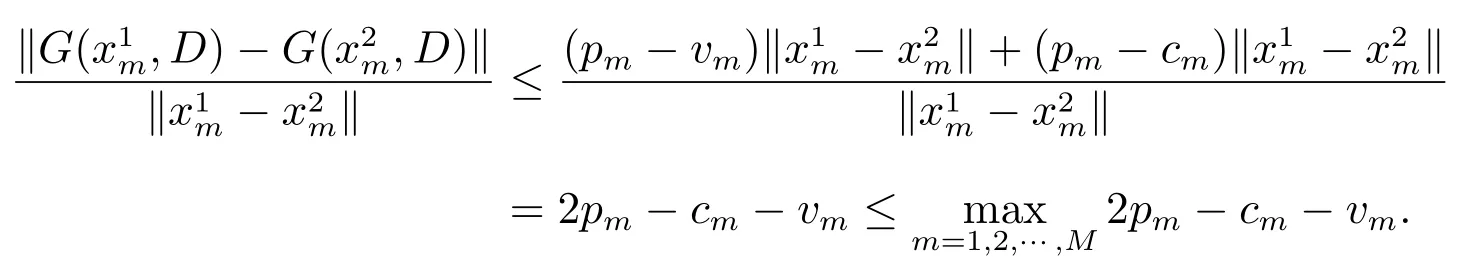
故而J(x,D), G(x,D)關(guān)于x 的Lipschitz 系數(shù)為

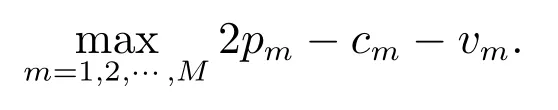
對(duì)于結(jié)論(ii)，由(i)可知，f(x)和h(x,η)關(guān)于x 是全局Lipschitz 連續(xù)的，Lipschitz系數(shù)為k．又因?yàn)镠(x,η,D)關(guān)于η 是全局Lipschitz 連續(xù)的，即

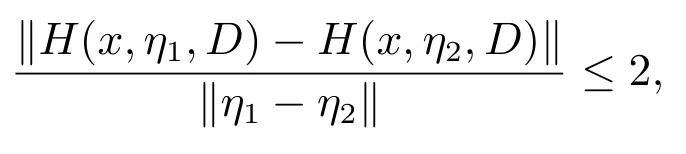
表明h(x,η)關(guān)于η 也是全局Lipschitz 連續(xù)的．

假設(shè)1問(wèn)題(4)滿足一致占優(yōu)條件(Slater 約束規(guī)范)，即存在x0∈X，使得

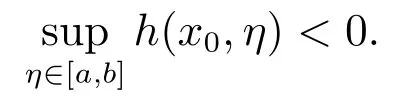
令

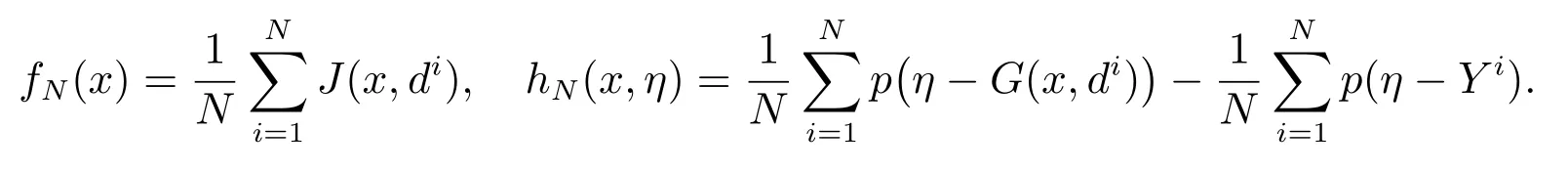
SAA 問(wèn)題(5)，可以寫(xiě)成如下形式

設(shè)問(wèn)題(6)的最優(yōu)值是zN，接下來(lái)證明隨樣本量N 的增加，zN收斂于真問(wèn)題(4)的最優(yōu)值，將樣本均值逼近寫(xiě)成特定的概率測(cè)度

在隨機(jī)規(guī)劃中，PN被稱為經(jīng)驗(yàn)概率測(cè)度．據(jù)此將(6)式改寫(xiě)為

在進(jìn)行收斂性分析之前定義以下幾個(gè)符號(hào)：設(shè)P(?)表示所有Borel 概率測(cè)度的集合；定義函數(shù)集

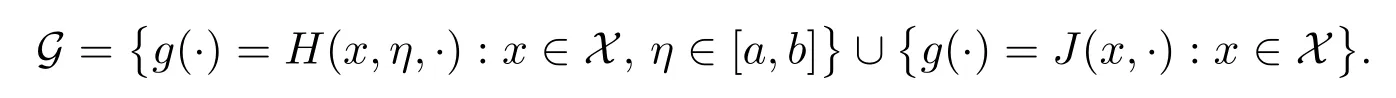
定義PN到P 的偽距離

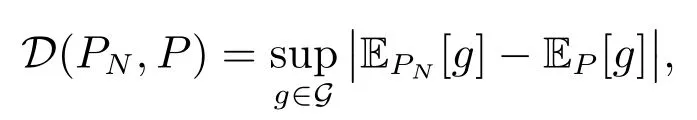
由于H(x,η,·)和J(x,·)是連續(xù)的，且X 和[a,b]是緊集，所以PN, P ∈ PG(?)且D(PN,P)<∞．

定理1設(shè)：

(i) 假設(shè)1 成立；

(ii) 命題1 的條件成立及X 是緊集，則：

1) 對(duì)于問(wèn)題(6)的最優(yōu)值函數(shù)V(PN)，當(dāng)N →∞時(shí)，w.p.1 滿足

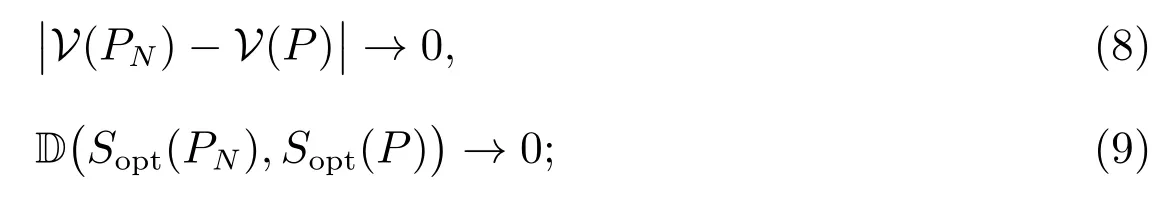
2) 若另有：

(iii) 對(duì)任意的x ∈X，當(dāng)t 趨向于0 時(shí)，廣義矩函數(shù)

有界，則對(duì)任意小的正數(shù)γ，存在正整數(shù)N?和獨(dú)立于N 的正實(shí)數(shù)C(γ), β(γ)，使得當(dāng)N ≥N?時(shí)，滿足

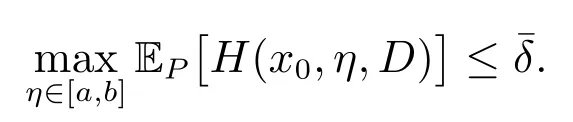
繼而由文獻(xiàn)[23]定理3.1 的結(jié)論(i)和文獻(xiàn)[34]定理2.7 的結(jié)論(iii)可知，存在正整數(shù)L?>0，使得w.p.1

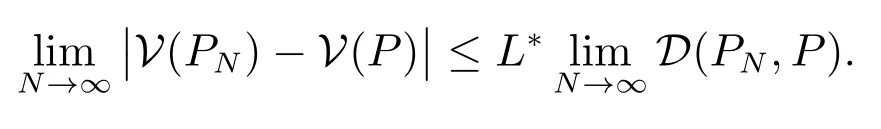
又由命題1 和文獻(xiàn)[23]命題3.1 可知，當(dāng)N →∞時(shí)，有D(PN,P)→0，所以有

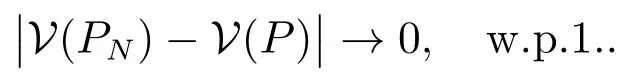
對(duì)于(9)式，在命題1 及假設(shè)1 的條件下，由文獻(xiàn)[34]定理2.7 的結(jié)論(ii)可知Sopt(·)在P 處上半連續(xù)．結(jié)合文獻(xiàn)[23]命題3.1 可知

對(duì)于(10)式，在條件(iii)下，由命題1 和文獻(xiàn)[23]命題3.2 可知，對(duì)任意小的正數(shù)γ ≤ L???，存在正整數(shù)N?和獨(dú)立于N 的正實(shí)數(shù)C(γ), β(γ)，當(dāng)N ≥ N?時(shí)

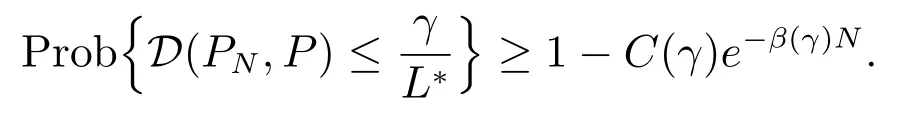
結(jié)合文獻(xiàn)[34]定理2.7 的結(jié)論(iii)，有

4 數(shù)值實(shí)驗(yàn)

由于問(wèn)題(5)是半無(wú)限問(wèn)題，難以求解，所以考慮在特定條件下將其轉(zhuǎn)化為有限問(wèn)題，即考慮其以下等價(jià)形式．

假設(shè)2隨機(jī)變量Y(D)的支持集Y ?[a,b]．

在假設(shè)2 下，由文獻(xiàn)[20]的命題3.2 可知問(wèn)題(5)等價(jià)于

稱問(wèn)題(5)與問(wèn)題(11)均為SAA 問(wèn)題．由于問(wèn)題(5)與(11)的等價(jià)性，所以在以下部分以(11)為研究對(duì)象．

4.1 切平面算法

Sun 等[26]改進(jìn)的切平面法適用于解決多個(gè)非線性復(fù)雜約束的隨機(jī)優(yōu)化問(wèn)題，這里采用該方法求解問(wèn)題(11)．

算法1

第1 步令迭代次數(shù)t=0，誤差?=10?5，令S0={x|0 ≤ cTx ≤ α}；

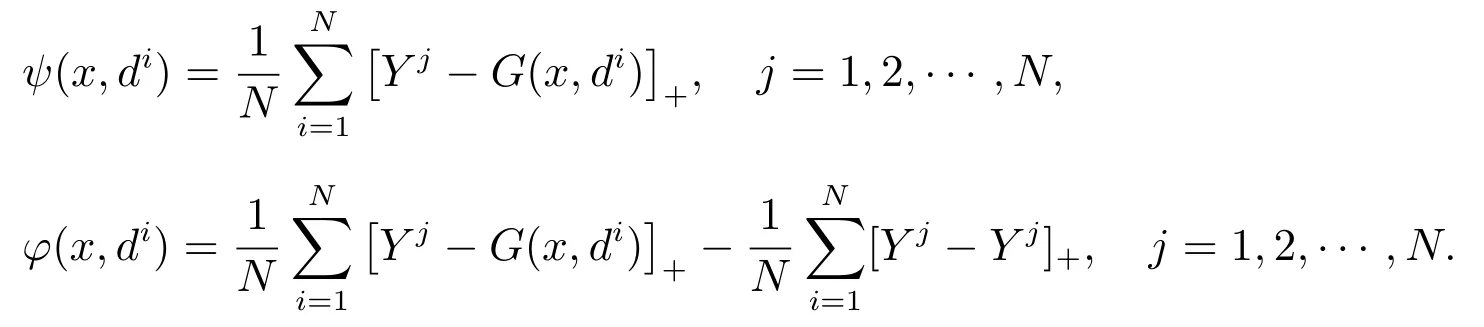
第2 步解決線性規(guī)劃問(wèn)題

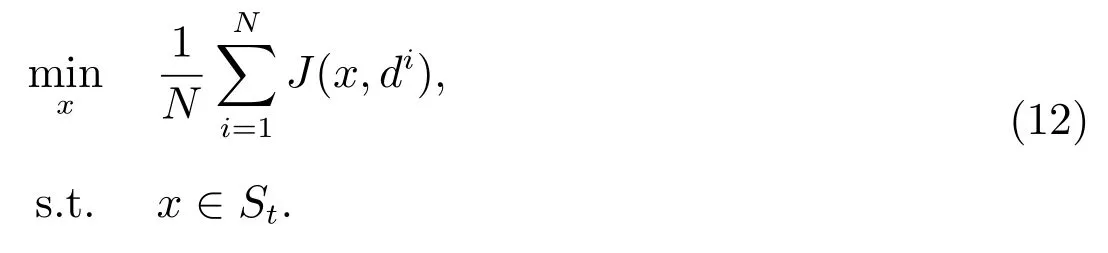
若問(wèn)題(12)無(wú)可行解，則原問(wèn)題無(wú)可行解；否則，設(shè)問(wèn)題(12)的最優(yōu)解為xt．

第3 步找到，使得

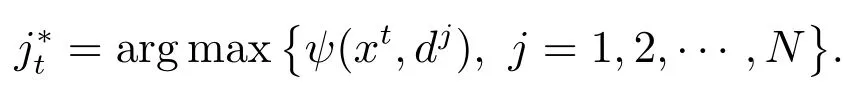
其實(shí)質(zhì)是找到眾多約束中違反度最大的約束．構(gòu)造索引集

第 4 步若停止，是最優(yōu)解；否則，構(gòu)造切平面

轉(zhuǎn)到第2 步．

4.2 實(shí)驗(yàn)及結(jié)果分析

本節(jié)考慮零售商需要在銷(xiāo)售季進(jìn)行五種產(chǎn)品的交易，即零售商需要在期初確定五種產(chǎn)品的訂購(gòu)量以期獲取最大利潤(rùn)．假定五種產(chǎn)品的需求服從不同自由度的χ2分布

在此基礎(chǔ)上設(shè)置三個(gè)示例，例1 采用模型(1)為參照進(jìn)行樣本內(nèi)實(shí)驗(yàn)，對(duì)SSD 模型的收斂性進(jìn)行驗(yàn)證．例2 在模型(1)為參照下，進(jìn)行樣本外累計(jì)預(yù)測(cè)．例3 以均值-方差(MV)模型為參照模型，進(jìn)行樣本外累計(jì)預(yù)測(cè)．MV 模型即以最小(大)化隨機(jī)損失(利潤(rùn))的期望為目標(biāo)函數(shù)，以隨機(jī)函數(shù)的方差來(lái)度量風(fēng)險(xiǎn)．對(duì)于報(bào)童問(wèn)題帶有訂購(gòu)能力約束的MV模型為

其中μ為常數(shù)，該模型也是風(fēng)險(xiǎn)厭惡模型．由于參照模型的最優(yōu)解也屬于緊集X，所以參照隨機(jī)變量Y(D)的支持集有界，假設(shè)2 成立，從而SAA 問(wèn)題(5)與(11)等價(jià)，這里采用算法1 求解問(wèn)題(11)．

例1SSD 模型收斂性分析數(shù)值實(shí)驗(yàn)

設(shè)資金約束α = 3.5，樣本量取10000，求得模型(1)的最優(yōu)解，作為SSD 模型的參照．然后在SSD 模型的求解中，樣本量依次設(shè)為100、1000、2000、3500、5500．每個(gè)樣本量下進(jìn)行30 次實(shí)驗(yàn)，其結(jié)果如圖1 所示，圖中每一個(gè)垂直區(qū)間表示在對(duì)應(yīng)樣本量下30 個(gè)最優(yōu)解的范圍．該圖顯示了SSD 模型下最優(yōu)解隨樣本量增大而逐漸收斂的特性．

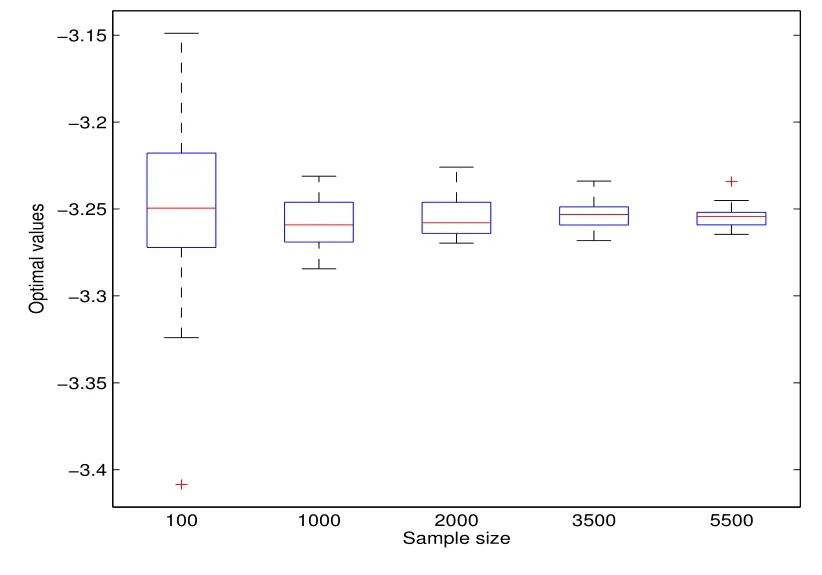
圖1: 例1 隨樣本量增加SAA 問(wèn)題的收斂性

例2以模型(1)為參照的SSD 模型樣本外累計(jì)預(yù)測(cè)

假設(shè)零售商在有限購(gòu)買(mǎi)能力下訂購(gòu)商品并出售，而后將利潤(rùn)累計(jì)到資本，直到最優(yōu)訂購(gòu)量的金額不受資本約束為止．樣本量N 取3000，初始資本設(shè)為0.7，在此條件下，本例在每輪訂購(gòu)下均進(jìn)行10 次抽樣，求得樣本外預(yù)測(cè)的利潤(rùn)均值，以該均值作為資本累計(jì)，經(jīng)過(guò)5 輪累計(jì)之后，累計(jì)資本大于最優(yōu)訂購(gòu)量下的成本，停止累計(jì)．

本例資本累計(jì)的步驟如下：

步驟1在相同初始資本下，模型(1)與SSD 模型各自以其最優(yōu)訂購(gòu)策略實(shí)現(xiàn)其預(yù)期利潤(rùn)；

步驟2模型(1)以其自身利潤(rùn)為累計(jì)資本，求得最優(yōu)解；

步驟3模型(1)以SSD 模型利潤(rùn)為累計(jì)資本，求得最優(yōu)利潤(rùn)作為基準(zhǔn)；在該基準(zhǔn)下，SSD 模型以其自身利潤(rùn)為累計(jì)資本，求得最優(yōu)解；

步驟4返回步驟2．

表1 和圖2 均說(shuō)明，在同樣的樣本下，平均利潤(rùn)SSD 模型優(yōu)于模型(1)．圖3 顯示了第四次樣本外累計(jì)預(yù)測(cè)10 次抽樣的結(jié)果，此時(shí)在訂購(gòu)能力約束下，SSD 模型下的利潤(rùn)高于模型(1)，這就使得在SSD 模型下，零售商可實(shí)現(xiàn)以更快的速度達(dá)到累計(jì)資本的目的，以擺脫訂購(gòu)能力約束．圖4 顯示了第五次樣本外累計(jì)預(yù)測(cè)10 次抽樣的結(jié)果，表明當(dāng)累計(jì)資本充足，即零售商不再受訂購(gòu)能力約束時(shí)，SSD 模型能夠以更少的投資獲得更大的利潤(rùn)．

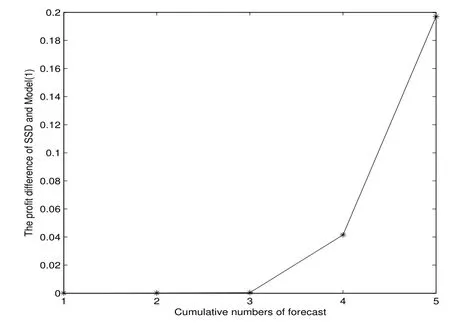
圖2: 例2 樣本外累計(jì)預(yù)測(cè)平均利潤(rùn)差

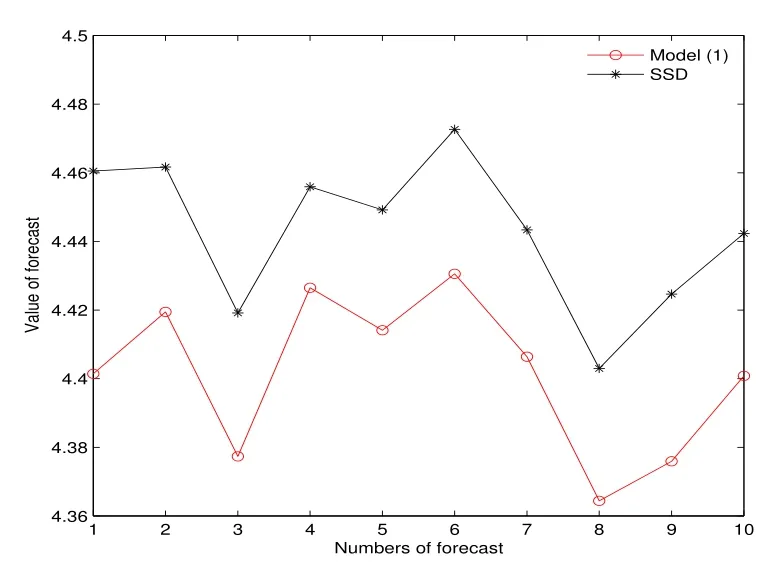
圖3: 例2 第四次預(yù)測(cè)

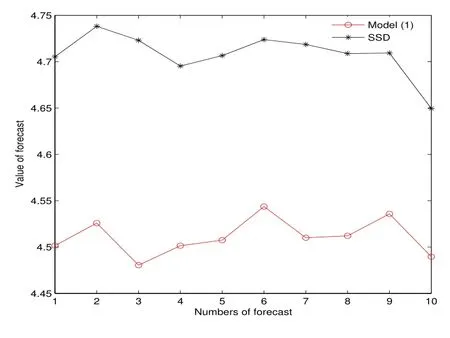
圖4: 例2 第五次預(yù)測(cè)

例3以MV 模型為參照的SSD 模型樣本外累計(jì)預(yù)測(cè)

采用例2 的資本累計(jì)步驟，以MV 模型為參照，設(shè)μ=0.3，所得結(jié)果如表2、圖5 至圖7 所示．

表2、圖5 至圖7 表明，樣本外累計(jì)預(yù)測(cè)下，SSD 模型的利潤(rùn)優(yōu)于MV 模型，且這種占優(yōu)趨勢(shì)隨著資本累計(jì)越來(lái)越明顯．其中圖6 和圖7 分別為第四次、第五次樣本外10 次抽樣的利潤(rùn)．

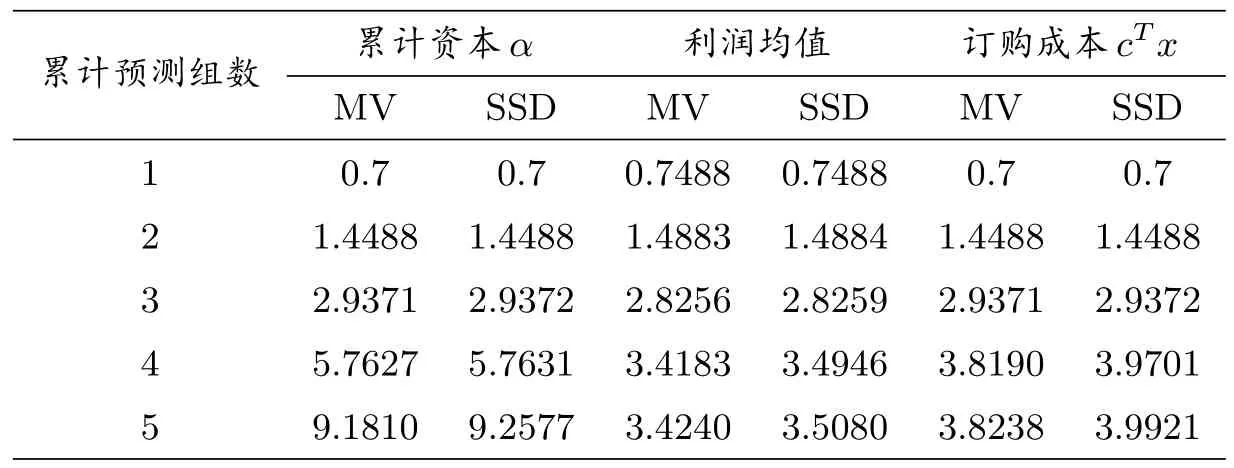
表2: 例3 樣本外累計(jì)預(yù)測(cè)

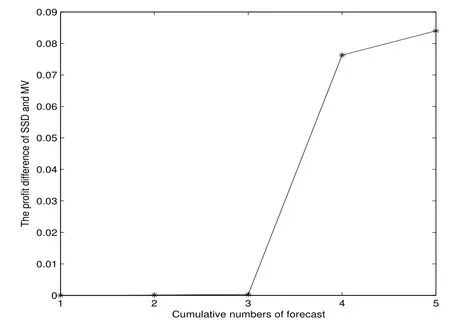
圖5: 例3 樣本外累計(jì)預(yù)測(cè)平均利潤(rùn)差

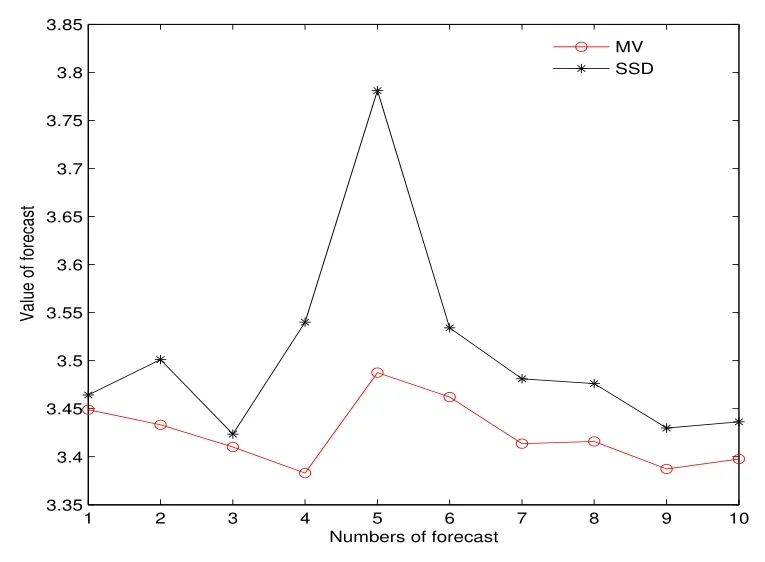
圖6: 例3 第四次預(yù)測(cè)

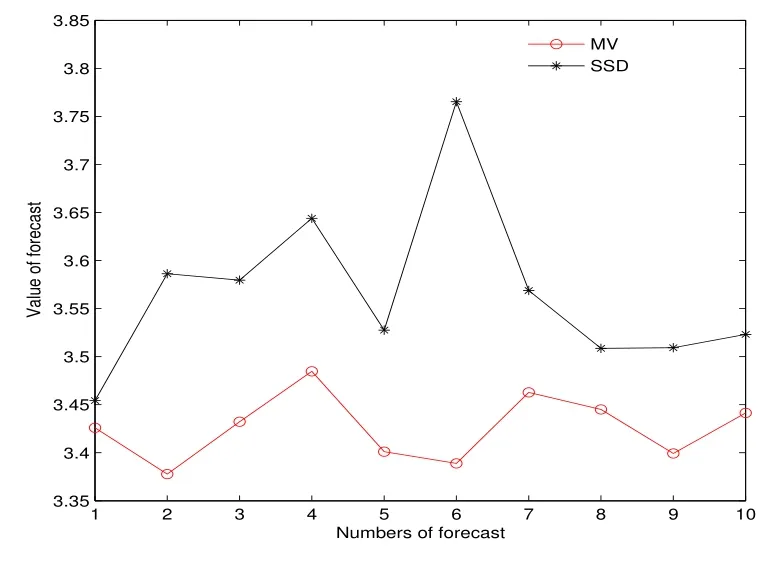
圖7: 例3 第五次預(yù)測(cè)

5 總結(jié)

本文以單周期多產(chǎn)品報(bào)童問(wèn)題為背景，在訂購(gòu)能力約束及SSD 約束下進(jìn)行建模．對(duì)SAA 問(wèn)題進(jìn)行收斂性分析并通過(guò)切平面法對(duì)SAA 問(wèn)題進(jìn)行求解．以風(fēng)險(xiǎn)中性模型(模型(1))及風(fēng)險(xiǎn)厭惡模型(MV 模型)為參照下，通過(guò)樣本外預(yù)測(cè)表明了SSD 模型的優(yōu)越性．SSD 模型具有良好的風(fēng)險(xiǎn)規(guī)避性，決策者可以該模型的訂購(gòu)策略作為自身決策的評(píng)價(jià)和基準(zhǔn)，具有重要的現(xiàn)實(shí)意義．基于本文的研究可以繼續(xù)探討多產(chǎn)品多周期的情形，以及風(fēng)險(xiǎn)厭惡條件下多級(jí)供應(yīng)鏈的協(xié)調(diào)等．