求解Poisson方程改進的交替方向隱式迭代格式

葛志昊, 劉富豪

(河南大學數學與統計學院，開封 475004)

1 引言

Poisson 方程是一類非常基礎且重要的物理方程，在圖像修復[1]、計算流體力學[2]、熱源識別[3]等領域均有重要應用．因此，構造一種簡便而且快速的求解Poisson 方程的算法是很有必要的．交替方向隱式迭代法具有比一般迭代法更高的收斂速度[4,5]，歷史上第一個交替方向隱式迭代法是由Peaceman 和Rachford 于1955 年在文獻[6]中提出的．1962 年，Varga 將交替方向隱式迭代法用于求解橢圓方程[4]，并將其命名為Peaceman-Rachford iterative method，簡稱PR 迭代法．該方法廣泛應用于各種凸優化問題[7,8]．

經典的交替方向隱式迭代格式[5]在計算大規模問題時，會產生諸多計算上的不便與缺點，如計算程序編寫困難、計算耗時較長、計算過程中占用內存過大等．為了克服上述缺點，本文給出了改進的交替方向隱式迭代格式，相比于經典的交替方向隱式迭代格式，改進的交替方向隱式迭代格式通過求解較低維數的矩陣方程，降低了程序實現難度，大大減少了計算量，并進一步證明了改進的交替方向隱式迭代格式與經典的交替方向隱式迭代格式的等價性．因此，改進的交替方向隱式迭代格式更加便于存儲，同時克服了經典的交替方向隱式迭代格式在計算上的缺點．

本文其余部分結構如下：在第2 部分的2.1 節，我們介紹經典的交替方向隱式迭代格式；在2.2 節，我們給出改進的交替方向隱式迭代格式；在2.3 節，我們證明經典的交替方向隱式迭代格式和改進的交替方向隱式迭代格式之間的等價性．在第3 部分，我們給出數值算例驗證改進的交替方向隱式迭代格式在計算量和程序實現等方面的優勢．最后，給出結論總結改進的交替方向隱式迭代格式的優勢和不足．

2 改進的交替方向隱式迭代格式

考慮Poisson 方程Dirichlet 邊值問題

其中

下面，對? 進行矩形網格剖分．取定沿x 軸，y 軸的步長h1和h2，作兩族與坐標軸平行的直線

兩族直線的交點(ih1,jh2)稱為網點或節點，記為(xi,yj)．

問題(1)和(2)的五點差分格式為

其中uij表示解函數u(x,y)在節點(xi,yj)處的數值解，fij=f(xi,yj)．

2.1 經典的交替方向隱式迭代格式

首先，我們給出矩陣的自然排列的定義．

定義1給定U =(uij)m×n∈ Rm×n，令

稱向量u 為矩陣U 的自然排列，并記作u = {uij}，其中U(:,j)T表示矩陣U 的第j 列的轉置．

下面，我們介紹經典的交替方向隱式迭代格式[4,5]：考慮問題(1)和(2)的五點差分格式(3)和(4)，定義矩陣L1和L2分別為

由(5)和(3)，得

于是，經典的交替方向隱式迭代格式(以下簡稱：經典的迭代格式)為

其中τk是迭代參數．按層合并，可得

2.2 改進的交替方向隱式迭代格式

接下來，我們給出改進的交替方向隱式迭代格式：考慮問題(1)和(2)的五點差分格式(3)和(4)，定義矩陣分別為

由(10)，可將(3)寫成

于是，改進的交替方向隱式迭代格式(以下簡稱：改進的迭代格式)為

其中τk是迭代參數．按層合并，得

2.3 改進的迭代格式與經典的迭代格式的等價性

定理1改進的迭代格式(13)和(14)與經典的迭代格式(8)和(9)等價．

證明 只需證明(8)與(13)的等價性，可以類似證明(9)與(14)的等價性，這里不再贅述．

考慮內點(xi,yj)處的五點差分格式．在(8)中u 的排列方式為自然排列．因此，點(xi,yj)處的數值解uij對應于向量u 中的第m(j?1)+i 個分量，而對應于矩陣U 第i 行第j 列的元素．

不失一般性，選取(8)中第m(j ?1)+i 個方程和(13)第i 行，第j 列的方程．

由 (8)，可知矩陣 I + τkL1的第 m(j ? 1)+i 行為

矩陣 I ? τkL2的第 m(j ? 1)+i 行為

由(15)和(16)，知(8)的第m(j ?1)+i 個方程為

同理，可得(13)第i 行，第j 列的方程為

經化簡，可以看出(17)與(18)相同．因此，在正則內點處，兩種方法建立的方程是等價的．

對于非正則內點處，我們可以在(17)和(18)中取i = 1,m (j = 1,2,··· ,n)和j =1,n (i=1,2,··· ,m)，并將邊界條件 u0,j=um+1,j=ui,0=ui,n+1=0 (i=1,2,··· ,m,j =1,2,··· ,n)代入其中得到．于是，兩種迭代格式建立的方程是等價的．

2.4 改進的迭代格式的優勢

雖然，經典的迭代格式在每一次迭代過程中，只需交替解兩個具有三對角系數矩陣的方程(8)和(9)，但L1, L2均為mn×mn 的三對角矩陣，而且L1L2．這不僅會增大問題的計算難度，而且會增加許多計算量．

改進的迭代格式在每次迭代過程中，需要交替求解兩個較低維數的具有三對角系數矩陣的矩陣方程(13)和(14)，這等價于求解n 個m×m 和m 個n×n 具有三對角系數矩陣的線性方程組，而且這兩個矩陣方程的三對角系數矩陣在U 為方陣的情況下是相等的，區別僅在于：在(13)中，系數矩陣左乘未知矩陣，在(14)中，系數矩陣右乘未知矩陣，相比于經典的交替方向隱式迭代格式，這是比較容易處理的．

為了比較兩種迭代格式在實際計算中的不同，現基于Gauss 消去法對求解(8)和(9)與(13)和(14)的過程，進行計算量的預估．若使用追趕法[9]對上面四個方程進行求解，則求解(8)和(9)的算法總計算量為

求解(13)和(14)的算法總計算量為

對比(19)和(20)可以發現，在盡可能避開零參與運算的情況下，相比于經典的迭代格式，改進的迭代格式在計算量上減少了很多，表1 和表2 也證實了這一點．事實上，經典的迭代格式在實際計算中，若是盡可能避開零參與運算和存儲的情況，則會大大增加程序編寫的難度和長度．而改進的迭代格式在這方面，是遠遠優于經典的迭代格式的．另外，由于改進的迭代格式和經典的迭代格式是等價的，這個結論已在第2.3 節給出證明，所以改進的迭代格式在計算精度方面并沒有提升．但改進的迭代格式在數據存儲方面，相比于經典的的迭代格式要少得多，而且要比后者方便的多．

3 數值實驗

在問題(1)和(2)中，取

此時，問題(1)和(2)的精確解為

記

取步長

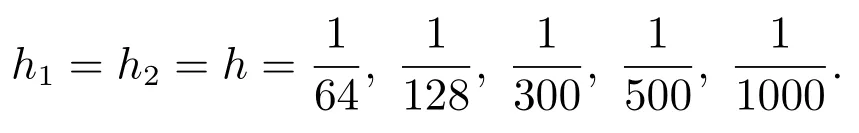
表1: 經典的迭代格式的誤差及運行時間

考慮迭代格式(13)和(14)，取步長

表2: 改進的迭代格式的誤差及運行時間

從表1 和表2 可以直觀地看出，利用改進的迭代格式的計算誤差與利用經典的迭代格式計算誤差并沒有明顯的差異，但在相同的步長下，經典的迭代格式用時遠遠超過改進的迭代格式，而且兩者之間的時間比也隨著步長h 的縮小而增大，如：當時，時間比為0.2188/0.1164 ≈ 1.9；當時，時間比為2.1853/0.4411 ≈5.0．對于經典的交替方向隱式迭代格式，當步長時，程序運行時間過長，而改進的迭代格式仍然很好．從圖1 和圖2 可以看出，步長越小，改進的迭代格式對真解的擬合效果越好．

圖1: 經典的迭代格式，(a)和(b)中的左圖為真解，右圖為數值解

圖2: 改進的迭代格式，(a)和(b)中的左圖為真解，右圖為數值解

由表1 和表2 中的數據可知，兩種迭代格式的誤差的差值在10?10范圍內，并且在以相同的步長和迭代停止條件下，兩種迭代格式的迭代步數相等，這說明在不考慮由求解器不同而產生的誤差時，每次迭代過程中的有效數據也是等價的，這與定理1 的結論一致．

4 結論

交替方向隱式迭代法是一種具有比一般迭代格式更高的收斂速度的求解Poisson 方程的方法，但經典的交替方向隱式迭代格式在當求解大規模問題時，會產生計算程序編寫困難，計算耗時較長，計算過程中占用內存過大等問題．本文給出了改進的交替方向隱式迭代格式(13)和(14)，通過求解較低維數的矩陣方程，降低了程序實現難度，大大減少了計算量．在計算量和程序實現等方面，改進的迭代格式(13)和(14)遠遠優于經典的迭代格式(8)和(9)．同時，本文證明了兩種迭代格式的等價性．因此，改進的迭代格式不僅具有經典的迭代格式在理論分析層面的收斂性，而且在計算上更加簡便快速．

然而，與經典的交替方向隱式迭代格式一樣，改進的交替方向隱式迭代格式僅適用求解區域為矩形區域或可以轉化為矩形求解區域的線性問題和半線性問題．本文以五點差分格式為基礎，導出改進的交替方向隱式迭代格式，事實上，仿照文中的過程，可以以九點差分格式導出更高階的交替方向隱式迭代格式，九點差分格式下的改進的交替方向隱式迭代格式與五點差分格式下的迭代格式在計算過程方面的區別僅在于：五點差分格式得到的迭代格式需要求解兩個系數矩陣為三對角矩陣的線性矩陣方程，而九點差分格式下的迭代格式需要求解兩個系數矩陣為五對角矩陣的線性矩陣方程，在兩個方向取的節點數相同的情況下，同一差分格式對應的矩陣方程系數矩陣是相等的．